自动化工具 pytest 内核测试平台落地初体验
测试平台,有人说它鸡肋,有人说它有用,有人说它轮子,众说纷纭,不如从自身出发,考虑是否要做测试平台:
第 1 阶段,用 Python+requests 写接口自动化。
第 2 阶段,选择 unitttest 或 pytest,更熟悉 pytest 选了 pytest。
第 3 阶段,快速搭建 pytest 项目脚手架,封装 tep 测试工具。
第 4 阶段,通过 Git 管理测试脚本,多分支合并代码。
第 5 阶段,去除本地环境同步麻烦,方便团队共享脚本。
需要有个测试平台。
使用篇
环境变量
环境变量是字符串键值对,全局作用域。比如不同环境不同域名:
使用:env_vars.name。
fixtures
fixtures 即 pytest 的 fixture,可以添加自定义函数,供测试用例使用。比如封装登录接口返回 token: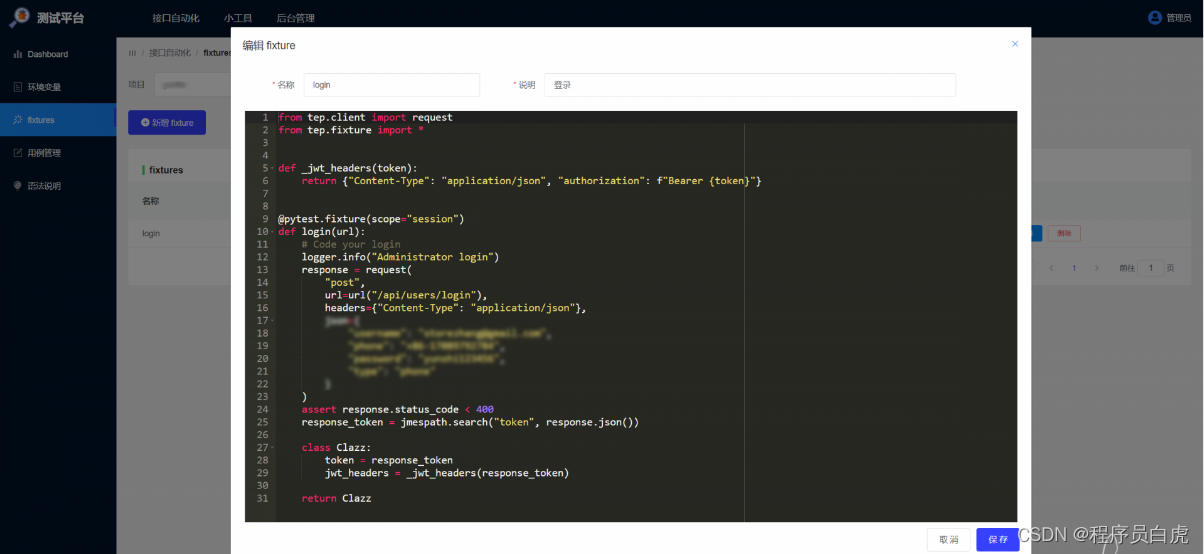
测试用例
在前端网页写代码,1 条用例对应 1 个 pytest 的test_name.py文件。比如调用login fixture 登录: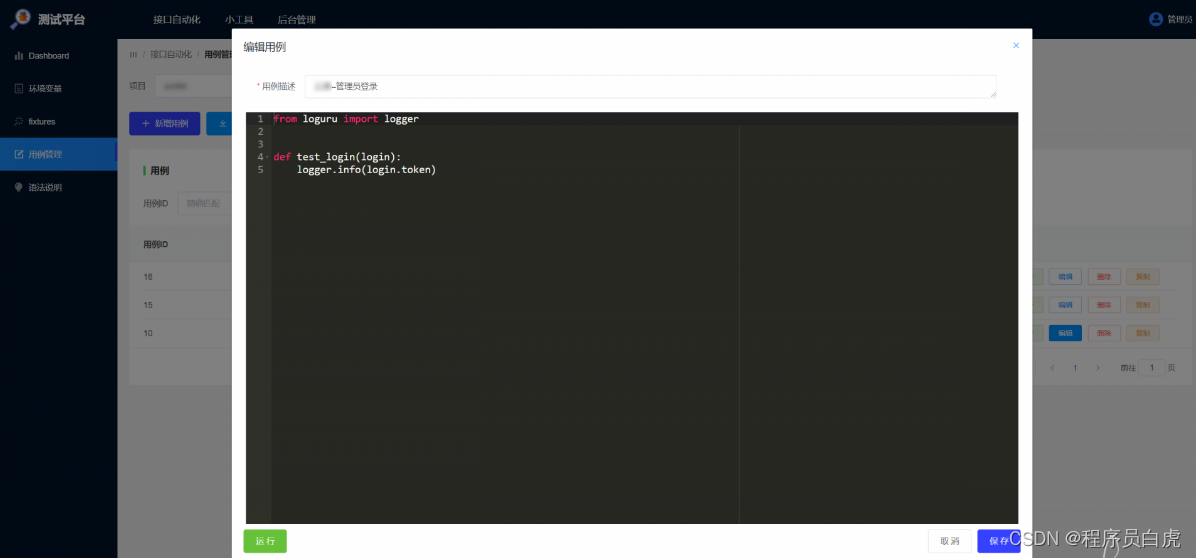
本地编写
PyCharm 写代码体验更好,正确姿势是从平台下载包含环境变量和 fixtures 等项目结构代码,本地编写用例,调试,跑通后,粘贴到平台上共享和维护:
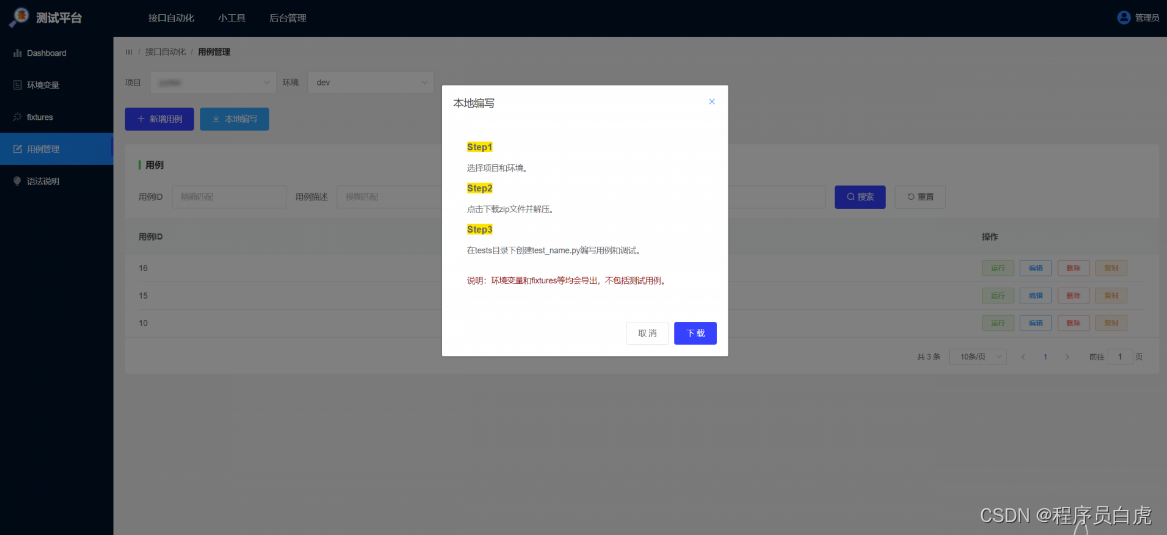
扩展能力
用例是 Python 代码,理论上所有 Python 能写出来的,平台都能支持,比如 HTTP、WebSocket、Protobuf 等协议。
原理篇
pytest 内核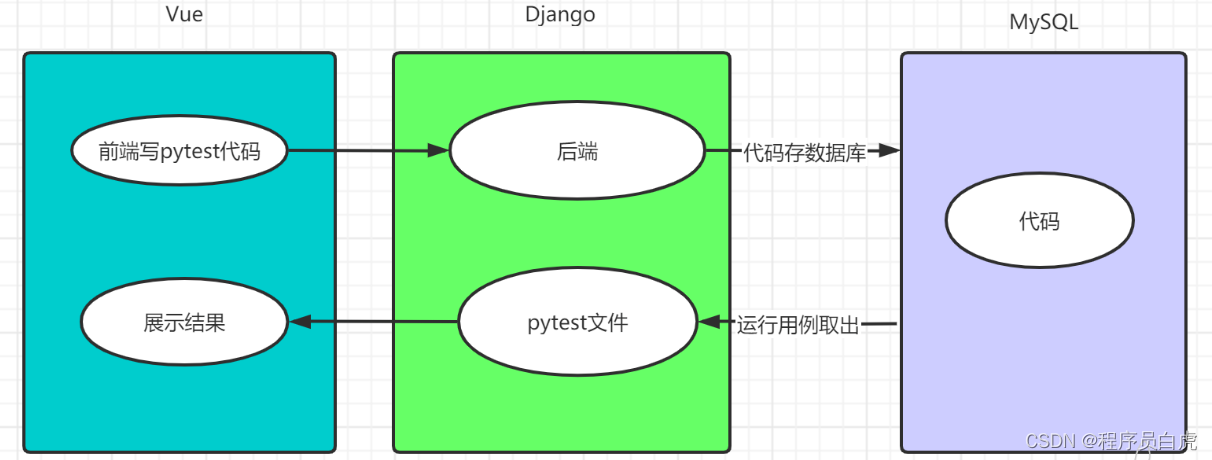
vue2-ace-editor作为前端代码编辑组件。
前端把代码通过 HTTP 请求传给后端。
后端把代码存入 MySQL 数据库。
运行用例,从数据库取出代码,生成 pytest 文件。
Shell 命令调用pytest -s test_name.py,执行测试。
后端把运行结果日志返给前端展示。
之所以要折腾数据库,是因为每次部署后 docker 容器里面的文件会被清掉,只能动态生成。
tep 脚手架
测试平台功能是从 tep 项目脚手架中抽取出来的: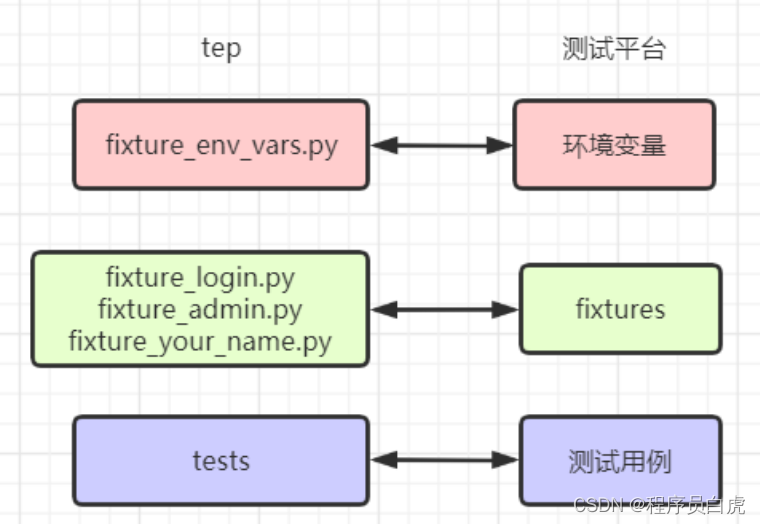
- 把
fixture_env_vars.py做成了环境变量功能。 - 把
fixture_login.py等做成了fixtures功能。 - 把
tests做成了测试用例功能。
运行用例
整体流程如下:
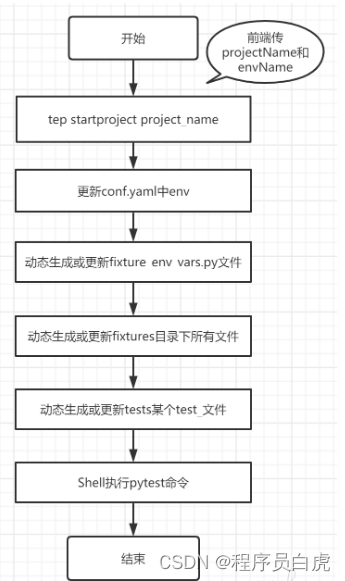
tep startproject project_name
运行用例时,判断项目目录是否存在,如果不存在就调用tep startproject project_name创建项目脚手架。
更新 conf.yaml 中 env
把前端传的当前运行环境更新到conf.yaml文件中:
动态生成或更新 fixture_env_vars.py 文件
根据环境变量功能模块的数据,动态生成fixture_env_vars.py文件:

动态生成或更新 fixtures 目录下所有文件
根据fixtures功能模块的数据,动态生成fixture_login.py等所有文件:
动态生成或更新 tests 某个 test_文件
从数据库拿到用例代码,动态生成test_文件。
Shell 执行 pytest 命令
从上一步拿到case_path,调用pytest -s case_path执行测试。
计划后续添加 suite 和 marker 两种批量执行用例方式。
【资源分享】
下面这份资源,对于想学习【软件测试】的朋友来说应该是最全面最完整的备战仓库,希望也能帮助到你!
相关文章:

自动化工具 pytest 内核测试平台落地初体验
测试平台,有人说它鸡肋,有人说它有用,有人说它轮子,众说纷纭,不如从自身出发,考虑是否要做测试平台: 第 1 阶段,用 Pythonrequests 写接口自动化。 第 2 阶段,选择 unit…...
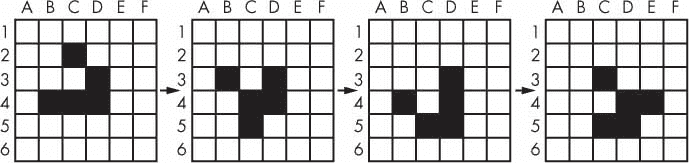
Python 自动化指南(繁琐工作自动化)第二版:四、列表
原文:https://automatetheboringstuff.com/2e/chapter4/ 在开始认真编写程序之前,您需要理解的另一个主题是列表数据类型及其表亲元组。列表和元组可以包含多个值,这使得编写处理大量数据的程序更加容易。由于列表本身可以包含其他列表&#…...
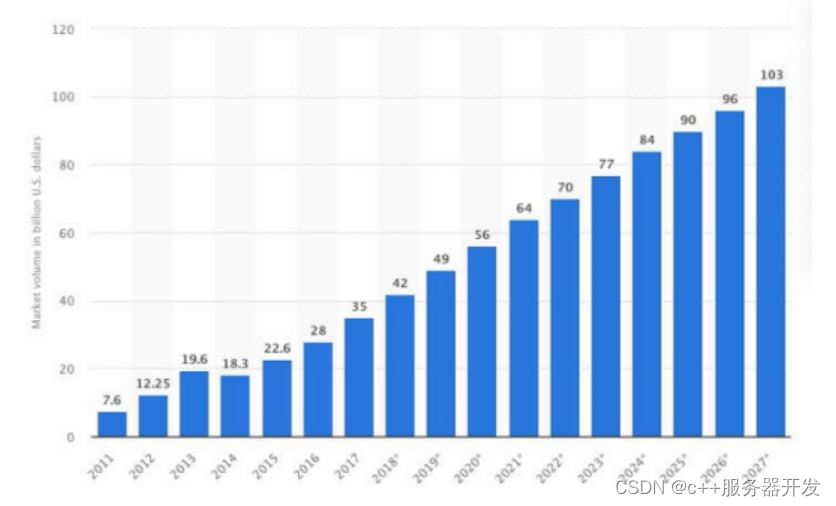
大数据领域的发展及其对现实世界的价值
大数据已经成为全球各行业领域不可或缺的一部分,并且其应用不断涌现。尽管很多人最初对“大数据”这一术语表示怀疑和不信任,但大数据技术已经确立了稳定的发展方向。根据调研机构的预测,到2027年,全球大数据市场规模将达到1090亿…...
几种常见的架构模式
本文已经收录到Github仓库,该仓库包含计算机基础、Java基础、多线程、JVM、数据库、Redis、Spring、Mybatis、SpringMVC、SpringBoot、分布式、微服务、设计模式、架构、校招社招分享等核心知识点,欢迎star~ Github地址 如果访问不了Github,…...

flutter安装各种问题汇总
C:\Users\Administrator>flutter doctor -v Flutter assets will be downloaded from https://storage.flutter-io.cn. Make sure you trust this source! [√] Flutter (Channel stable, 3.7.0, on Microsoft Windows [版本 10.0.19044.1826], locale zh-CN) • Flutte…...
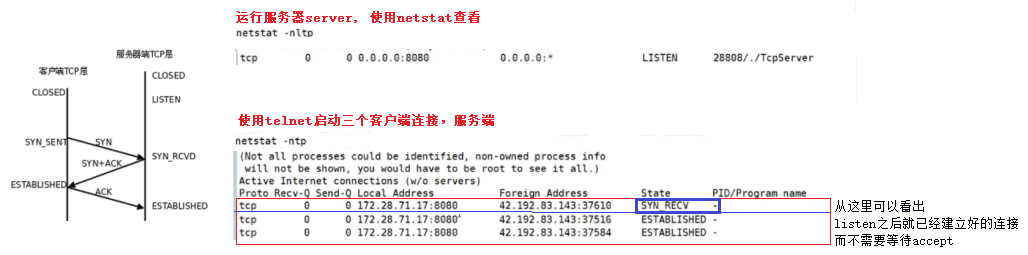
网络传输层
目录传输层再谈端口号端口号范围划分认识知名端口号netstatpidofUDP协议UDP协议端格式UDP的特点面向数据报UDP的缓冲区UDP使用注意事项使用udp协议 的应用层协议其它TCP协议TCP协议段格式如何理解链接如何理解三次握手如何理解四次挥手概念TIME_WAIT/CLOSE_WAITTCP策略确认应答…...
)
linux内核启动分析(二)
文章目录1. set_task_stack_end_magic2.smp_setup_processor_id3. debug_objects_early_init4. cgroup_init_early4.1 init_cgroup_root4.1.1 init_cgroup_housekeeping4.2 cgroup_init_subsys5. local_irq_disable5.1 raw_irqs_disabled5.2 raw_local_irq_disable5.3 trace_ha…...

『EasyNotice』.NET开源消息通知组件——快速实现邮件/钉钉告警通知
📣读完这篇文章里你能收获到 傻瓜式扩展方法直接使用如何通过EasyNotice快速实现钉钉/邮件的通知发送感谢点赞收藏,避免下次找不到~ 文章目录一、EasyNotice1. 功能介绍2. 源码地址二、项目接入1. 发送邮件通知Step 1 : 安装包,通过Nuget安装…...
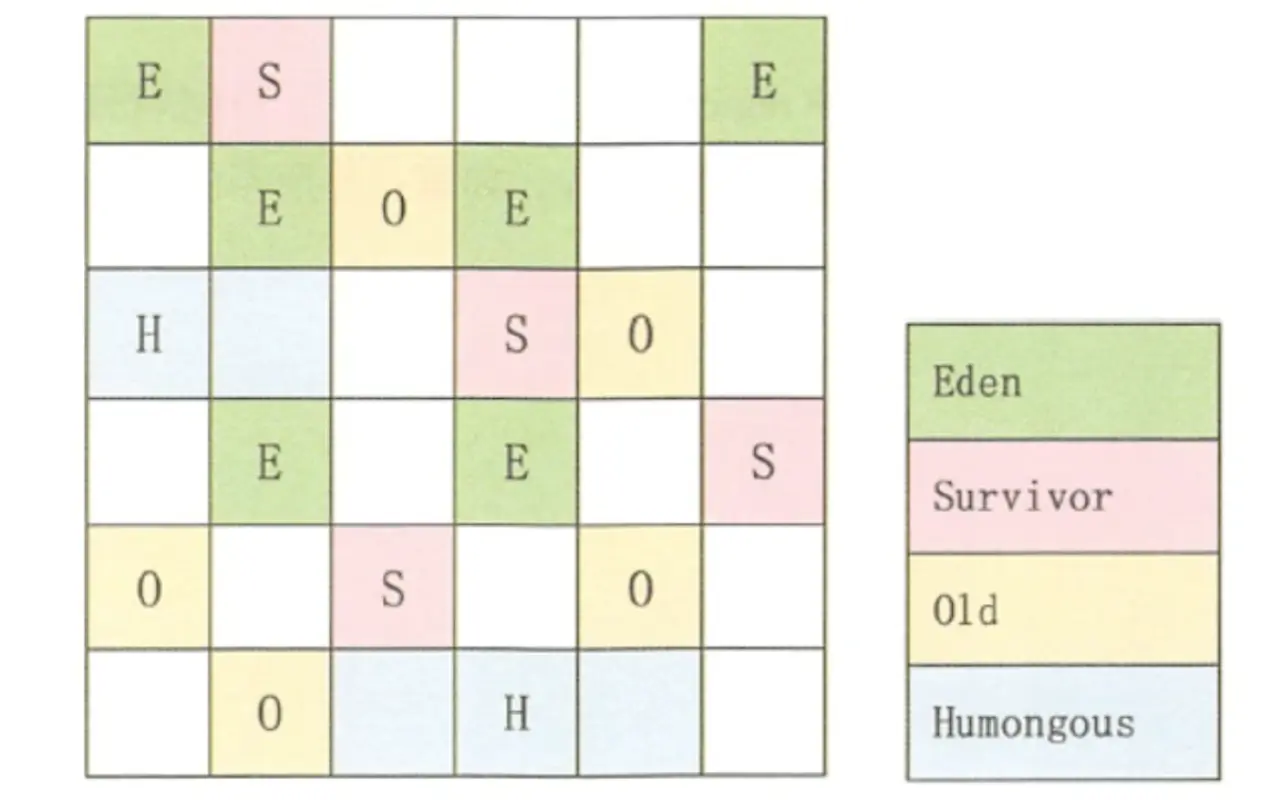
JVM垃圾回收算法
垃圾标记阶段 对象存活判断:在堆里存放着几乎所有的Java对象实例,在GC执行垃圾回收之前,首先需要区分出内存中哪些是存活对象,哪些是已经死亡的对象。只有被标记为己经死亡的对象,GC才会在执行垃圾回收时,…...

怎么看待ChatGPT封号这件事呢?
最近的ChatGPT大量封号,刷爆了全网,我的两个个人账号被封禁了,不知道大家最近有没有遇到相关的报错信息,要么就是检查你当前的浏览器配置,最后来一个access denied,要么直接就给你来一个当前的国家不支持。…...

八、交换技术原理
(一)交换机 1、交换机介绍 一种用于电(光)信号转发的网络设备,可以为接入交换机的任意两个网络节点提供独享的电信号通路。 工作于第二层的叫交换机,工作于第三层的叫第三层交换机,最常见的是…...
)
什么是DHCP?DHCP有什么用?(中科三方)
在IP网络中,每一个连接的设备都需要分配一个唯一的IP地址,才能实现和Internet上其他设备的互联。在一些终端规模较大的网络中,需要为每一个主机手工配置IP地址,以避免IP地址的重复,如果主机发生变更,还要去…...
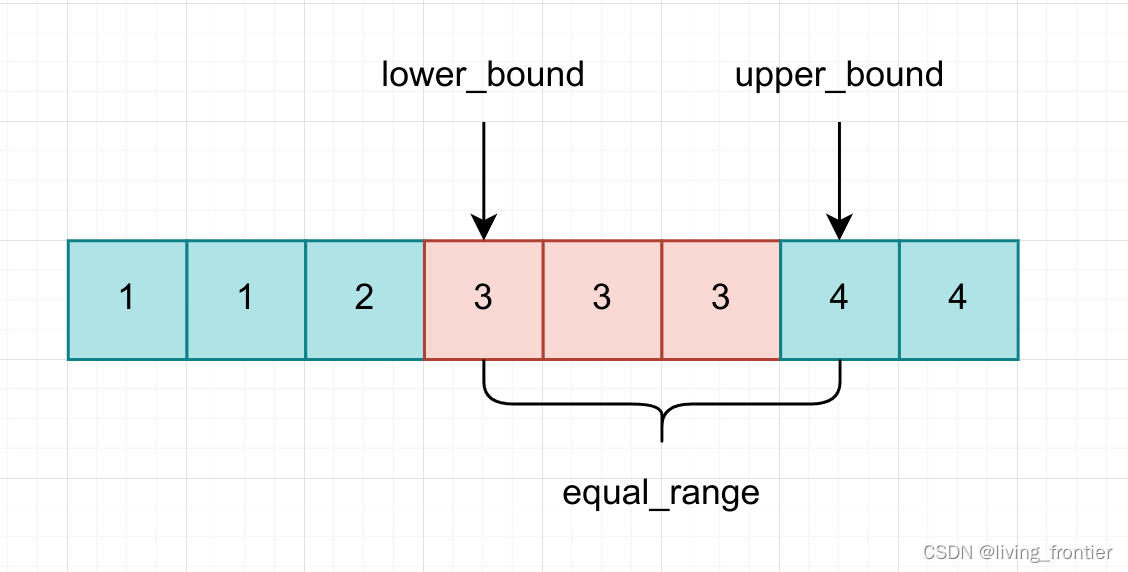
算法设计-二分
一、有序和单调 二分本质上是一种更加智能的搜索状态空间的方式,他需要状态空间的状态呈现一种“有序的一维数组”的形式,然后再进行搜索。所以一开始的排序是无法避免的。 因为二分的写法问题,所以应当怎样排序也是有一定讲究的&…...
隧道技术基础
隧道技术基础基本概念端口转发应用层代理基本概念 攻击者通过边界主机进入内网,往往会利用它当跳板进行横向渗透,但现在的内部网络大多部署了很多安全设备,网络结构错综复杂,对于某些系统的访问会受到各种阻挠,这就需…...
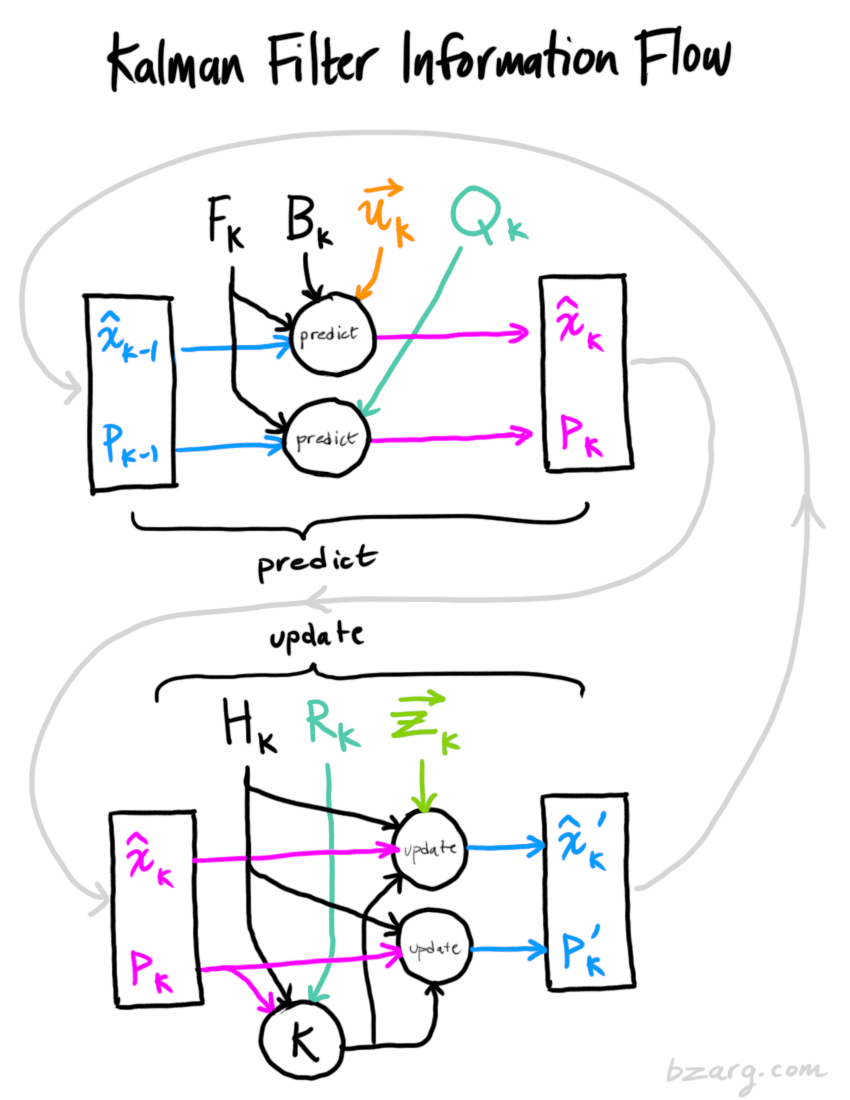
卡尔曼滤波浅析
文章目录前言任务状态预测外部影响因素外部不确定性状态更新利用测量进一步修正状态合并两个高斯分布公式汇总图形化解释总结(readme)references前言 Kalman Filter算法,是一种递推预测滤波算法,算法中涉及到滤波,也涉…...

Eolink Apikit 创建/生成 API 文档
在 API 研发管理产品中,几乎所有的协作工作都是围绕着 API 文档进行的。 我们在接触了大量的客户后发现,采用 文档驱动 的协作模式会比先开发、后维护文档的方式更好,团队协作效率和产品质量都能得到提高。因此我们建议您尝试基于文档来进行工…...

2023年上半年系统分析师备考法则
截止3月30日,上海、北京等地都开始报名,部分省市已经截止报名,大家如果还没报名成功的赶紧报名,千万别错过了,另外就是别忘了缴费,缴费成功才是报名成功。 报名网址:https://bm.ruankao.org.cn…...

【人工智能】—约束传播、弧约束、问题结果与问题分解、局部搜索CSP
【人工智能】—约束传播、弧约束、问题结果与问题分解、局部搜索CSP约束传播弧约束弧相容算法AC-3问题结构化简约束图-树结构CSP问题的局部搜索CSP的迭代算法举例:4-Queens加速:模拟退火法加速:最小最大优化(约束加权法)小结约束传播 前向检…...

Java设计模式面试专题
1.请列举出在 JDK 中几个常用的设计模式? 单例模式(Singleton pattern)用于 Runtime,Calendar 和其他的一些类中。工厂模式(Factory pattern)被用于各种不可变的类如 Boolean,像 Boolean.value…...

文件(下)——“C”
各位CSDN的uu们你们好呀,今天,小雅兰的内容是文件的知识点,下面,就让我们进入文件的世界吧 文件的顺序读写 文件的随机读写 fseek ftell rewind 文本文件和二进制文件 文件读取结束的判定 文件缓冲区 在上篇博客中,…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

【SQL学习笔记1】增删改查+多表连接全解析(内附SQL免费在线练习工具)
可以使用Sqliteviz这个网站免费编写sql语句,它能够让用户直接在浏览器内练习SQL的语法,不需要安装任何软件。 链接如下: sqliteviz 注意: 在转写SQL语法时,关键字之间有一个特定的顺序,这个顺序会影响到…...

服务器--宝塔命令
一、宝塔面板安装命令 ⚠️ 必须使用 root 用户 或 sudo 权限执行! sudo su - 1. CentOS 系统: yum install -y wget && wget -O install.sh http://download.bt.cn/install/install_6.0.sh && sh install.sh2. Ubuntu / Debian 系统…...

省略号和可变参数模板
本文主要介绍如何展开可变参数的参数包 1.C语言的va_list展开可变参数 #include <iostream> #include <cstdarg>void printNumbers(int count, ...) {// 声明va_list类型的变量va_list args;// 使用va_start将可变参数写入变量argsva_start(args, count);for (in…...

FFmpeg avformat_open_input函数分析
函数内部的总体流程如下: avformat_open_input 精简后的代码如下: int avformat_open_input(AVFormatContext **ps, const char *filename,ff_const59 AVInputFormat *fmt, AVDictionary **options) {AVFormatContext *s *ps;int i, ret 0;AVDictio…...

DiscuzX3.5发帖json api
参考文章:PHP实现独立Discuz站外发帖(直连操作数据库)_discuz 发帖api-CSDN博客 简单改造了一下,适配我自己的需求 有一个站点存在多个采集站,我想通过主站拿标题,采集站拿内容 使用到的sql如下 CREATE TABLE pre_forum_post_…...

【HarmonyOS 5】鸿蒙中Stage模型与FA模型详解
一、前言 在HarmonyOS 5的应用开发模型中,featureAbility是旧版FA模型(Feature Ability)的用法,Stage模型已采用全新的应用架构,推荐使用组件化的上下文获取方式,而非依赖featureAbility。 FA大概是API7之…...

EEG-fNIRS联合成像在跨频率耦合研究中的创新应用
摘要 神经影像技术对医学科学产生了深远的影响,推动了许多神经系统疾病研究的进展并改善了其诊断方法。在此背景下,基于神经血管耦合现象的多模态神经影像方法,通过融合各自优势来提供有关大脑皮层神经活动的互补信息。在这里,本研…...

Python异步编程:深入理解协程的原理与实践指南
💝💝💝欢迎莅临我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 持续学习,不断…...
