逼近理论及应用精解【12】
文章目录
- 卷积
- 卷积层与滤波层
- 定义
- 数学原理与公式
- 定理
- 架构
- 例子
- 例题
- 卷积层和滤波层概念的详细解释
- 卷积层
- 滤波层
- 滤波层和卷积层在卷积神经网络(CNN)中区别
- 滤波层
- 卷积层
- 总结
- 卷积层的数学原理
- 滤波层的数学原理
- 参考文献
卷积
卷积层与滤波层
定义
- 卷积层:卷积层(Convolutional Layer)是卷积神经网络(Convolutional Neural Network,CNN)中的核心组件,它通过卷积运算对输入数据进行特征提取。
- 滤波层:在卷积神经网络中,滤波层通常指的是卷积层,其中卷积核(Convolution Kernel)也称为滤波器(Filter)。卷积核是一个较小的矩阵,用于提取输入数据的局部特征。
数学原理与公式
- 卷积运算:卷积运算是一种数学运算,用于两个函数之间的积分。在图像处理中,卷积运算通常表示为对输入图像与滤波器(卷积核)进行点积运算。卷积层的数学原理基于卷积运算,通过滑动窗口的方式在输入图像上移动卷积核,计算每个位置的点积,从而生成特征图(Feature Map)。
- 卷积层公式:卷积层的输出特征图大小计算公式为 W o u t = ( W i n − k + 2 P ) / S + 1 W_{out}=(W_{in}-k +2P)/S+1 Wout=(Win−k+2P)/S+1,其中 W o u t W_{out} Wout 是输出特征图的宽度, W i n W_{in} Win 是输入图像的宽度, k k k 是卷积核的大小, P P P 是填充(Padding)的像素数, S S S 是步长(Stride)。
- 卷积层计算:卷积层的计算包括定位卷积核、元素级乘积和求和、滑动卷积核等步骤。卷积核在输入图像上滑动,在每个位置上进行元素级的乘积并求和,从而生成一个输出值。这个过程会重复多次以生成完整的特征映射。
定理
- 卷积定理:卷积定理是傅立叶变换满足的一个重要性质。它指出,函数卷积的傅立叶变换等于函数傅立叶变换的乘积。这一定理在信号处理、通信系统等领域有广泛应用。
架构
- 卷积神经网络架构:卷积神经网络通常由多个卷积层、池化层、激活层等交叉堆叠而成。卷积层负责特征提取,池化层用于降采样和减少计算量,激活层引入非线性特性。
例子
- 边缘检测:在图像处理中,卷积层可以通过使用特定的卷积核(如Sobel算子)来检测图像中的边缘。边缘检测是卷积层在图像处理中的一个典型应用。
例题
-
例题1:假设输入图像大小为5x5,卷积核大小为3x3,步长为1,无填充。计算输出特征图的大小。
- 解:根据卷积层输出特征图大小的计算公式, W o u t = ( W i n − k + 2 P ) / S + 1 W_{out}=(W_{in}-k +2P)/S+1 Wout=(Win−k+2P)/S+1,其中 W i n = 5 W_{in}=5 Win=5, k = 3 k=3 k=3, P = 0 P=0 P=0, S = 1 S=1 S=1。代入公式得 W o u t = ( 5 − 3 ) / 1 + 1 = 3 W_{out}=(5-3)/1+1=3 Wout=(5−3)/1+1=3,因此输出特征图的大小为3x3。
-
例题2:假设输入图像大小为8x8,卷积核大小为3x3,步长为2,填充为1。计算输出特征图的大小。
- 解:同样根据卷积层输出特征图大小的计算公式, W o u t = ( W i n − k + 2 P ) / S + 1 W_{out}=(W_{in}-k +2P)/S+1 Wout=(Win−k+2P)/S+1,其中 W i n = 8 W_{in}=8 Win=8, k = 3 k=3 k=3, P = 1 P=1 P=1, S = 2 S=2 S=2。代入公式得 W o u t = ( 8 − 3 + 2 ) / 2 + 1 = 4 W_{out}=(8-3+2)/2+1=4 Wout=(8−3+2)/2+1=4,因此输出特征图的大小为4x4。
综上所述,卷积层与滤波层在卷积神经网络中扮演着至关重要的角色,它们通过卷积运算提取输入数据的局部特征,为后续的图像处理或分类任务提供关键信息。
卷积层和滤波层概念的详细解释
卷积层
卷积层(Convolutional Layer)是卷积神经网络(Convolutional Neural Network,CNN)中的核心组件,它通过卷积运算对输入数据进行特征提取。
- 定义:卷积层由多个卷积单元组成,每个卷积单元的参数通过反向传播算法优化得到。卷积运算的目的是提取输入数据的局部特征。
- 数学原理:卷积层通过卷积核(Convolution Kernel)与输入特征图(通常是图像或其他类型的数据)进行卷积运算,提取出输入数据中的局部特征。这些特征可以是低级的,如边缘、纹理和颜色等,也可以是更高级别的抽象特征,这些特征在后续的网络层中会被进一步处理和组合,以形成更复杂的特征表示。卷积层中的每个卷积核都会在整个输入特征图上滑动,进行卷积运算。
- 参数共享和局部连接:卷积层通过参数共享和局部连接的方式大大减少了网络参数的数量,降低了模型的复杂度和计算成本,同时也减少了过拟合的风险。因为同一卷积核在滑动过程中使用的参数是固定的,这意味着它在学习输入数据的某种特征时,会将这种特征应用到整个输入数据上。
- 激活函数:为了引入非线性特性并增强模型的表达能力,卷积层通常会使用激活函数(如ReLU、Sigmoid和Tanh等)对输出特征图进行非线性转换。
滤波层
在卷积神经网络中,滤波层通常指的是卷积层,其中卷积核(Convolution Kernel)也称为滤波器(Filter)。
- 定义:滤波器是一个较小的矩阵,用于提取输入数据的局部特征。在卷积层中,滤波器(卷积核)通过滑动窗口的方式在输入数据上进行卷积运算,从而提取出输入数据中的局部特征。
- 结构:一个“kernel”更倾向于是2D的权重矩阵,而“filter”则是指多个Kernel堆叠的3D结构。如果是一个2D的filter,那么两者就是一样的。但是一个3D filter,在大多数深度学习的卷积中,它是包含kernel的。每个卷积核都是独一无二的,主要在于强调输入通道的不同方面。
- 作用:滤波器的作用是通过卷积运算提取输入数据的局部特征。这些特征可以是图像的边缘、线条、角等低级特征,也可以是更高级别的抽象特征。
综上所述,卷积层和滤波层在卷积神经网络中扮演着至关重要的角色,它们通过卷积运算和滤波操作提取输入数据的局部特征,为后续的图像处理或分类任务提供关键信息。
滤波层和卷积层在卷积神经网络(CNN)中区别
虽然都涉及到对输入数据的特征提取,但它们在实现细节和目的上存在一些区别。以下是滤波层和卷积层的主要区别:
滤波层
- 目的:滤波层的主要目的是通过滤波器(也称为卷积核)对输入数据进行特征提取。这些特征可以是图像的边缘、纹理、颜色等信息。
- 操作:滤波层通过滤波器在输入数据上进行滑动窗口操作,计算每个位置的点积,并生成输出特征图。在这个过程中,滤波器的大小、形状和权重都是固定的,不会随着输入数据的改变而改变。
- 特点:滤波层通常不会改变输入数据的大小,除非进行边界填充(Padding)或步长(Stride)不等于1的操作。滤波操作可以看作是卷积操作的一种特殊情况,其中卷积核不需要进行180度翻转。
卷积层
- 目的:卷积层的主要目的也是进行特征提取,但它通过卷积运算实现了更复杂的特征提取能力。卷积层能够学习到输入数据的空间层次结构,提取出更高级别的特征表示。
- 操作:卷积层中的卷积核在输入数据上进行滑动窗口操作,但在进行点积计算之前,通常需要将卷积核进行180度翻转。然后,将翻转后的卷积核与输入数据进行点积运算,生成输出特征图。卷积层还可以包含多个卷积核,每个卷积核都可以提取不同类型的特征。
- 特点:卷积层通过参数共享和局部连接的方式显著减少了网络参数的数量,降低了模型的复杂度。同时,卷积层还具有一定的平移不变性,即对输入数据进行平移后,卷积层的输出基本保持不变。这使得卷积层在处理图像等具有空间层次结构的数据时具有独特的优势。
总结
- 操作区别:滤波层通常不进行卷积核的翻转操作,而卷积层则需要进行180度翻转。
- 特征提取能力:卷积层通过参数共享和局部连接的方式实现了更复杂的特征提取能力,能够学习到输入数据的空间层次结构。而滤波层则更多地关注于局部特征的提取。
- 应用场景:滤波层在处理图像等具有空间层次结构的数据时可能不如卷积层有效,但在某些特定任务(如边缘检测)中可能表现出色。卷积层则更广泛地应用于各种图像处理和计算机视觉任务中。
总的来说,滤波层和卷积层在卷积神经网络中各有特点,它们共同构成了强大的特征提取机制,为后续的图像处理和分类任务提供了坚实的基础。
卷积层和滤波层在卷积神经网络(CNN)中的数学原理主要涉及到卷积运算,尽管滤波层在CNN中通常指的是卷积层,但在某些情况下,滤波层可能特指使用特定滤波器的卷积层。以下是对卷积层和滤波层数学原理的详细解释:
卷积层的数学原理
-
卷积运算:
- 卷积运算是一种线性运算,用于计算两个函数(在离散情况下是序列)之间的重叠量。在卷积神经网络中,卷积运算通常用于计算输入数据与卷积核(滤波器)之间的重叠量。
- 二维卷积运算的公式可以表示为:
Y ( i , j ) = ∑ m = 0 M − 1 ∑ n = 0 N − 1 X ( i + m , j + n ) ⋅ W ( m , n ) Y(i, j) = \sum_{m=0}^{M-1} \sum_{n=0}^{N-1} X(i+m, j+n) \cdot W(m, n) Y(i,j)=∑m=0M−1∑n=0N−1X(i+m,j+n)⋅W(m,n)
其中, X X X 是输入数据, W W W 是卷积核, Y Y Y 是输出特征图, M M M 和 N N N 分别是卷积核的高度和宽度。
-
参数共享:
- 卷积层通过参数共享机制显著减少了模型的参数量。在卷积运算中,同一个卷积核会在输入数据的不同位置进行滑动,并使用相同的权重进行计算。
- 这种参数共享机制使得卷积层能够学习到输入数据的空间层次结构,并提取出具有平移不变性的特征。
-
局部连接:
- 卷积层中的神经元只与输入数据的局部区域相连接,这种连接方式称为局部连接。
- 局部连接使得卷积层能够专注于输入数据的局部特征,并通过多层网络迭代提取更复杂的特征。
滤波层的数学原理
-
滤波器:
- 在卷积神经网络中,滤波器通常指的是卷积核。滤波器是一个较小的矩阵,用于提取输入数据的局部特征。
- 滤波器的尺寸、形状和权重都是可学习的参数,通过反向传播算法进行优化。
-
滤波操作:
- 滤波操作可以看作是卷积操作的一种特殊情况。在滤波层中,滤波器在输入数据上进行滑动窗口操作,计算每个位置的点积,并生成输出特征图。
- 与卷积层类似,滤波层也通过参数共享和局部连接的方式减少模型的参数量,并提取出输入数据的局部特征。
-
特定滤波器的应用:
- 在某些情况下,滤波层可能特指使用特定滤波器的卷积层。例如,在边缘检测任务中,可以使用Sobel滤波器来提取图像的边缘特征。
- 这些特定滤波器通常具有固定的权重和尺寸,用于实现特定的图像处理任务。
综上所述,卷积层和滤波层在卷积神经网络中的数学原理主要涉及到卷积运算、参数共享、局部连接以及特定滤波器的应用。这些原理共同构成了卷积神经网络强大的特征提取能力,为后续的图像处理和分类任务提供了坚实的基础。
参考文献
- 文心一言
相关文章:

逼近理论及应用精解【12】
文章目录 卷积卷积层与滤波层定义数学原理与公式定理架构例子例题 卷积层和滤波层概念的详细解释卷积层滤波层 滤波层和卷积层在卷积神经网络(CNN)中区别滤波层卷积层总结卷积层的数学原理滤波层的数学原理 参考文献 卷积 卷积层与滤波层 定义 卷积层…...

LIN总线学习大全(基于CANoe和CAPL)
🍅 我是蚂蚁小兵,专注于车载诊断领域,尤其擅长于对CANoe工具的使用🍅 寻找组织 ,答疑解惑,摸鱼聊天,博客源码,点击加入👉【相亲相爱一家人】🍅 玩转CANoe&…...
国庆作业
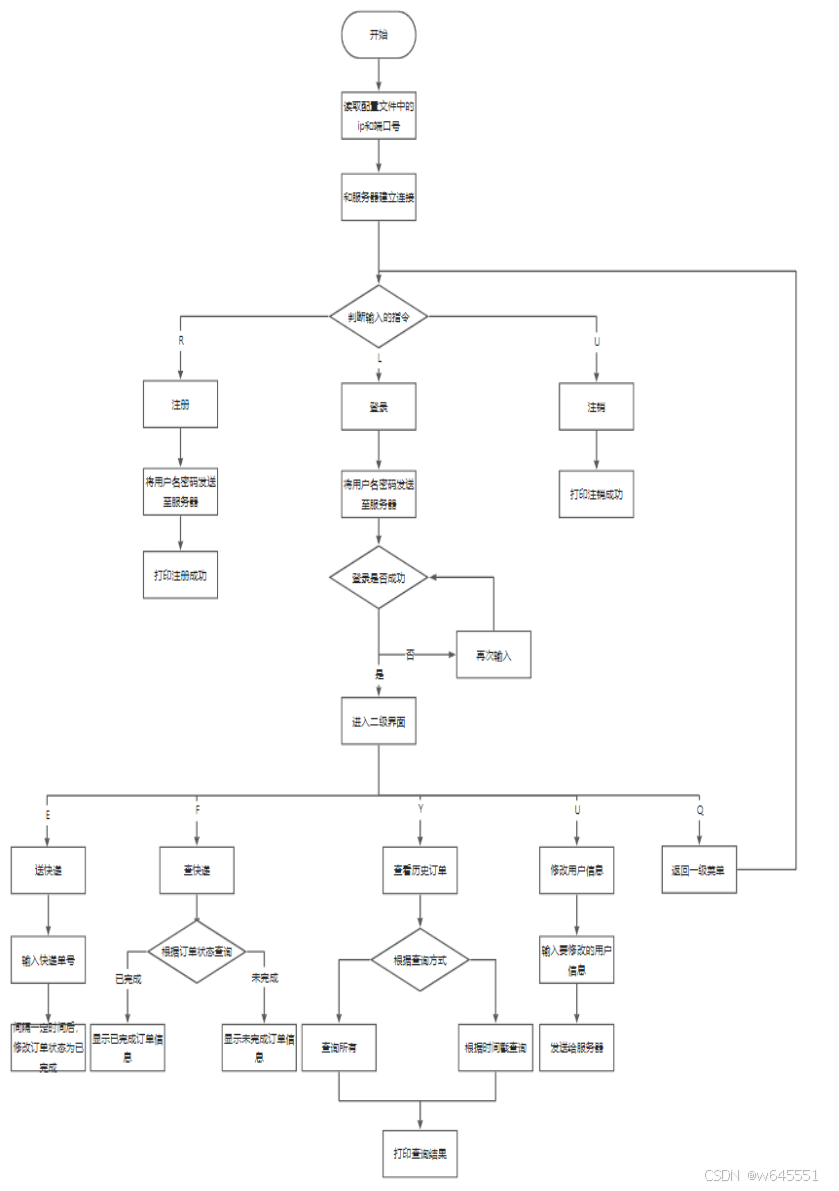
day1 1.开发环境 Linux系统GCCFDBmakefilesqlite3 2.功能描述 项目功能: 服务器:处理客户端的请求,并将数据存入数据库中,客户端请求的数据从数据库进行获取,服务器转发给客户端。 用户客户端:实现账号的注册、登…...
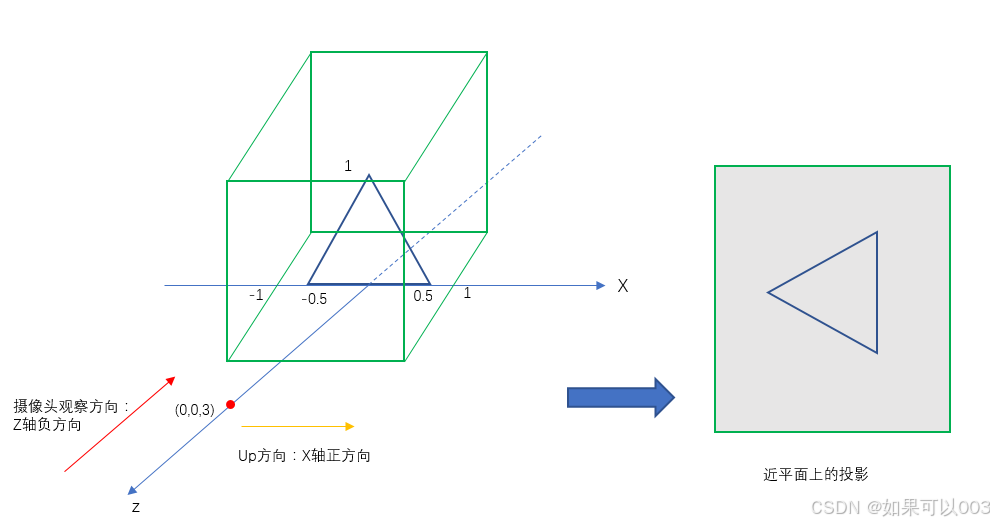
Android OpenGLES2.0开发(四):矩阵变换和相机投影
事物的本质是事物本身所固有的、深藏于现象背后并决定或支配现象的方面。 还记得我们上一篇绘制的三角形吗,我们确实能够顺利用OpenGL ES绘制出图形了,这是一个好的开始,但这还远远不够。我们定义的坐标是正三角形,但是绘制出…...
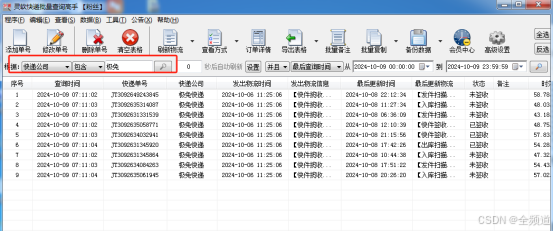
快递查询软件:实现单号识别与批量物流查询的高效工具
随着网络购物的普及,快递物流行业迎来了前所未有的发展机遇,同时也面临着巨大的挑战。跟踪物流信息成为一个难题,因此,快递查询软件的核心功能之一便是单号识别。传统的快递单号输入方式繁琐且易出错在此背景下,快递查…...
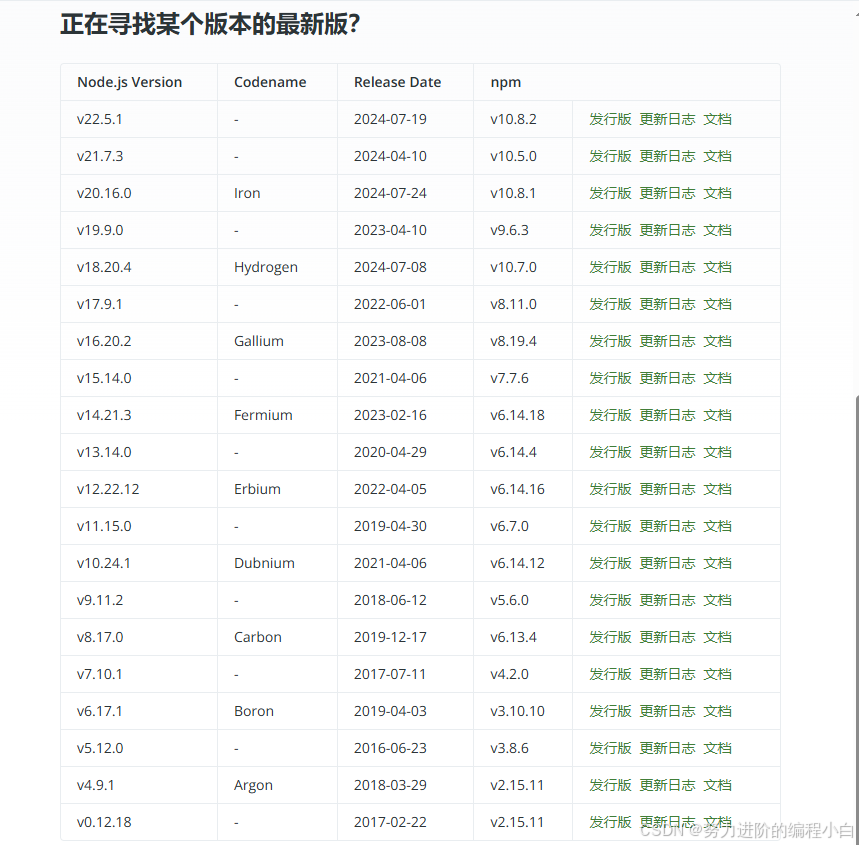
nodejs与npm版本对应表
Node.js — Node.js 版本 (nodejs.org)...

Spring Boot 项目中如何使用异步任务
前置知识: 同步任务: 同步任务是在单线程中按顺序执行,每次只有一个任务在执行,不会引发线程安全和数据一致性等并发问题 同步任务需要等待任务执行完成后才能执行下一个任务,无法同时处理多个任务,响应慢…...

Scrum实战中遇到的问题与解决方法
在当今快速变化的技术环境中,IT企业面临着持续的市场压力和竞争,传统的瀑布式开发模式已经难以满足现代企业的需要。瀑布模型过于僵化,缺乏灵活性,导致项目经常延期,成本增加,最终可能无法达到预期效果。为…...
全面介绍 Windows 录屏工具:开启录制新篇章
高质量的录屏工具是我们录屏的得力助手。但是日常因为侧重点的不同,比如有的喜欢录制游戏画面、有的需要录制教学视频、演示操作也需要录屏工具。这次我们就来探讨一下windows录屏工具有哪些吧。 1.福晰录屏大师 链接:www.foxitsoftware.cn/REC/ 从这…...

Maven 和 NetBeans:集成与使用
Maven 和 NetBeans:集成与使用 Maven 和 NetBeans 是两款强大的工具,常用于Java开发。Maven是一个项目管理工具,它能够帮助管理项目的构建、报告和文档。NetBeans是一个集成开发环境(IDE),它为Java开发提供了丰富的功能和友好的用户界面。将Maven集成到NetBeans中,可以…...

【系统架构设计师】目录提纲
一、绪论(TODO) 二、计算机与网络基础知识(TODO) 三、信息系统基础知识(TODO) 四、系统开发基础知识(TODO) 五、软件架构设计(TODO) 六、UML建模与架构文…...

【微服务】—SpringBoot入门
⭐⭐⭐⭐⭐⭐ Github主页👉https://github.com/A-BigTree 笔记仓库👉https://github.com/A-BigTree/tree-learning-notes 个人主页👉https://www.abigtree.top ⭐⭐⭐⭐⭐⭐ 文章目录 1 SpringBoot快速入门1.1 SpringBoot简介1.1.1 简介1.1.2…...

Linux: debug: perf: report: --sort
文章目录 简介实例简介 接上回:https://mzhan017.blog.csdn.net/article/details/142689870。 这里介绍perf的这个参数,还是非常的有用,尤其是分析对整个系统做perf record的数据,而不是单个进程做perf record。-s, --sort= : Sort histogram entries by given key(s) - …...

like 模糊查询的底层算法
like 模糊查询的底层算法 全文搜索算法、模糊查询、n-gram分隔算法功能介绍 百度搜索,文心一言给出的结果: SQL模糊查询底层通常使用全文搜索算法,如LIKE操作符和全文索引通常使用的n-gram分割算法。 n-gram是一种将文本分割成固定大小的词…...
【Linux实践】实验九:Shell流程控制语句
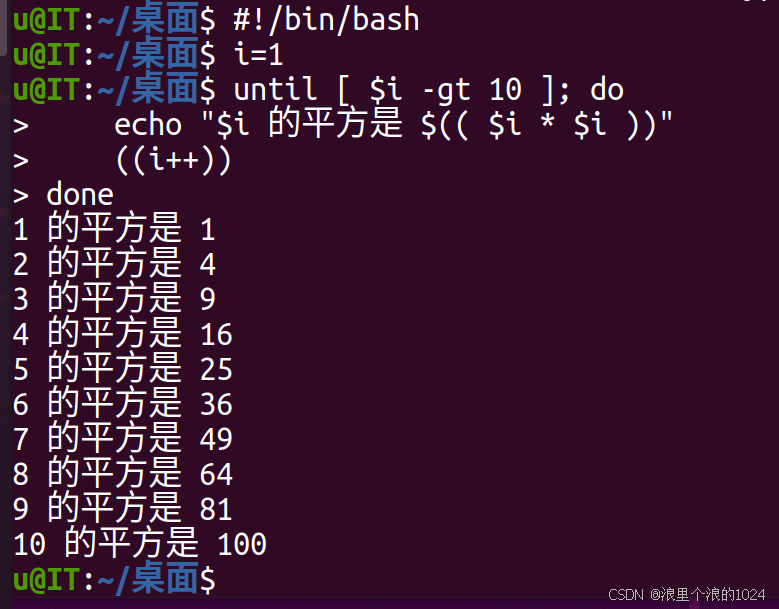
文章目录 实验九:Shell流程控制语句实验目的:实验内容:操作步骤:1. 复制*.c文件并排序2. 计算1-10的平方 实验九:Shell流程控制语句 实验目的: 掌握条件判断语句,如if语句、case语句。掌握循环…...
YOLOv8实战TT100K中国交通标志检测【数据集+YOLOv8模型+源码+PyQt5界面】
YOLOv8实战TT100k交通标志识别 文章目录 研究背景资源获取1.前言1.1 YOLO 系列:中国交通标志检测领域的璀璨明星1.2 Transformer与注意力机制:为中国交通标志检测注入新活力1.3 中国交通标志检测技术:迎接挑战,砥砺前行1.4 YOLOv8…...

SQLite3
文章目录 SQLite3 C/CAPI介绍SQLite3 C/C API 使⽤ SQLite3 C/CAPI介绍 C/C API是SQLite3数据库的⼀个客⼾端,提供⼀种⽤C/C操作数据库的⽅法。 SQLite3 C/C API 使⽤ 下⾯我们将这⼏个接⼝封装成⼀个类,快速上⼿这⼏个接口 创建/打开数据库文件针对打开…...

我的创作纪念日一年
目录 机缘 收获 日常 成就 憧憬 机缘 我之所以开始写CSDN博客,源于一段特殊的时光。去年此时,我独自待在实验室,周围的世界仿佛与我无关。没有旅游,没有与朋友的欢聚,情感的挫折和学业的压力如潮水般袭来。在这样的…...

Docker基本操作命令(一)
Docker 是一个开源的应用容器引擎,允许开发者打包应用以及其依赖包到一个可移植的容器中,然后发布到任何流行的 Linux 机器上,也可以实现虚拟化。容器是完全使用沙箱机制,相互之间不会有任何接口。主要功能是为开发者提供一个简单…...

PGMP-02项目集管理绩效域
目录 1.概要 2.defintions定义 3.Program Management Performance Domain interactions 交互 4. Organizational Strategy, Portfolio Management, and Program Management Linkage 5. Portfolio and Program Distinctions 区别 6. Program and Project Distinctions区别 …...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

uniapp中使用aixos 报错
问题: 在uniapp中使用aixos,运行后报如下错误: AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...

python报错No module named ‘tensorflow.keras‘
是由于不同版本的tensorflow下的keras所在的路径不同,结合所安装的tensorflow的目录结构修改from语句即可。 原语句: from tensorflow.keras.layers import Conv1D, MaxPooling1D, LSTM, Dense 修改后: from tensorflow.python.keras.lay…...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...

【Linux系统】Linux环境变量:系统配置的隐形指挥官
。# Linux系列 文章目录 前言一、环境变量的概念二、常见的环境变量三、环境变量特点及其相关指令3.1 环境变量的全局性3.2、环境变量的生命周期 四、环境变量的组织方式五、C语言对环境变量的操作5.1 设置环境变量:setenv5.2 删除环境变量:unsetenv5.3 遍历所有环境…...

libfmt: 现代C++的格式化工具库介绍与酷炫功能
libfmt: 现代C的格式化工具库介绍与酷炫功能 libfmt 是一个开源的C格式化库,提供了高效、安全的文本格式化功能,是C20中引入的std::format的基础实现。它比传统的printf和iostream更安全、更灵活、性能更好。 基本介绍 主要特点 类型安全:…...

车载诊断架构 --- ZEVonUDS(J1979-3)简介第一篇
我是穿拖鞋的汉子,魔都中坚持长期主义的汽车电子工程师。 老规矩,分享一段喜欢的文字,避免自己成为高知识低文化的工程师: 做到欲望极简,了解自己的真实欲望,不受外在潮流的影响,不盲从,不跟风。把自己的精力全部用在自己。一是去掉多余,凡事找规律,基础是诚信;二是…...

flow_controllers
关键点: 流控制器类型: 同步(Sync):发布操作会阻塞,直到数据被确认发送。异步(Async):发布操作非阻塞,数据发送由后台线程处理。纯同步(PureSync…...

python基础语法Ⅰ
python基础语法Ⅰ 常量和表达式变量是什么变量的语法1.定义变量使用变量 变量的类型1.整数2.浮点数(小数)3.字符串4.布尔5.其他 动态类型特征注释注释是什么注释的语法1.行注释2.文档字符串 注释的规范 常量和表达式 我们可以把python当作一个计算器,来进行一些算术…...
【工具教程】多个条形码识别用条码内容对图片重命名,批量PDF条形码识别后用条码内容批量改名,使用教程及注意事项
一、条形码识别改名使用教程 打开软件并选择处理模式:打开软件后,根据要处理的文件类型,选择 “图片识别模式” 或 “PDF 识别模式”。如果是处理包含条形码的 PDF 文件,就选择 “PDF 识别模式”;若是处理图片文件&…...
