逻辑回归(下): Sigmoid 函数的发展历史
背景
闲来无事翻了一下之前买的一个机器学习课程及之前记录的网络笔记,发现遇到公式都是截图,甚至是在纸上用笔推导的。重新整理一遍之前逻辑回归函数的学习笔记,主要是为了玩一下 LaTex 语法,写公式挺有意思的。
整理之前三篇笔记汇总如下:
- 逻辑回归(上):函数求导过程自推 LaTex 语法
- 逻辑回归(中):数学公式学习笔记 LaTeX 版
- 逻辑回归(下): Sigmoid 函数的发展历史
逻辑回归 S 曲线的发展历史
Sigmoid 这个S 形是怎么发展的呢?又怎么想到用它来做分类的呢?罗马不是一天建成的,Sigmoid 函数也不是一天形成的。逻辑回归的历史相当悠久,迄今大概已经有200年。它的前身,则在18世纪就已经出现了。
18世纪,随着工业革命的深入;世界经济、科技的发展;美洲的发现,以及随之而来的大移民和北美人口迅猛增长……各个学科对于统计学的工具性需求越来越强烈。到了19世纪,为了研究人口增长以及化学催化反应与时间的关系,人们发明了逻辑函数。
指数函数
这个大家都不陌生,这就是传说中增长最快的曲线,它的数学表达式为:
f ( x ) = a x f(x)=a^x f(x)=ax
最初,学者们将人口(或化合物)的数量与时间的函数定义为 W ( t ) W(t) W(t), t t t 代表时间变量, W ( t ) W(t) W(t) 代表总量,用指数函数表示为:
W ( t ) = a e b t ,其中 a , e , b 均为模型参数, t 为模型变量。 W(t)=ae^{bt},其中 a,e,b 均为模型参数,t 为模型变量。 W(t)=aebt,其中a,e,b均为模型参数,t为模型变量。
该函数在坐标系中的表现为:

用该模型为一个国家的人口进行建模,已经被证明在一个国家新建早期人口增长状况是复合该模型的。马尔克斯的人口论中讲述的「在没有任何外界阻碍的情况下,人口将以几何级增长」正是基于指数模型。
我还想到了各种投资理论提倡的复利、非线性增长等,也是基于这个模型。
对该函数求微分,就可以得到增长率函数:
W ′ ( t ) = d W ( t ) d t W^{'}(t)=\frac{dW(t)}{dt} W′(t)=dtdW(t)
修正指数函数
19世纪早期,开始有数学家、统计学家质疑上述模型:任何事物,如果真的按照几何级数任意增长下去,都会达到不可思议的数量。
然而,在自然界中,并没有什么东西是在毫无休止地增长的。当一种事物数量越来越多以后,某种阻力也会越来越明显地抑制其增长。
比利时数学家 Verhulst 给出了一个新的模型:
W ′ ( t ) = b W ( t ) − g ( W ( t ) ) W'(t)=bW(t)-g(W(t)) W′(t)=bW(t)−g(W(t))
其中, g ( W ( t ) ) g(W(t)) g(W(t))是以 W ( t ) W(t) W(t)为自变量的函数,它代表随着总数增长出现的阻力。
Verhulst 尝试了几种不同的阻力函数后,发现 g(W(t)) 是 W(t) 的平方形式时,新模型显示了它的逻辑性。对人口增长率公式修正,取 g ( ( W ( t ) ) = b ( W ( t ) ) 2 L g((W(t))=\frac{b(W(t))^2}{L} g((W(t))=Lb(W(t))2,其中 L 为 W(t) 的上限,增长率函数为:
W ′ ( t ) = b W ( t ) − b ( W ( t ) ) 2 L = b W ( t ) ( 1 − W ( t ) L ) \begin{align} W^{'}(t)&=bW(t)-\frac{b(W(t))^2}{L}\newline &=bW(t)(1-\frac{W(t)}{L})\newline \end{align} W′(t)=bW(t)−Lb(W(t))2=bW(t)(1−LW(t))
这个公式将增长率表现为总量 W(t)、极限值L、总量和极限值之间的差比之间的关系。
令 P ( t ) = W ( t ) L P(t)=\frac{W(t)}{L} P(t)=LW(t),使用商的求导公式 u = W ( t ) , v = L u=W(t),v=L u=W(t),v=L 计算该函数的微分:
P ′ ( t ) = W ′ ( t ) ∗ L + 0 ∗ L L 2 = W ′ ( t ) L 2 = W ′ ( t ) L \begin{align} P^{'}(t)&=\frac{W^{'}(t)*L+0*L}{L^2}\newline&=\frac{W^{'}(t)}{L^2}\newline &=\frac{W^{'}(t)}{L} \end{align} P′(t)=L2W′(t)∗L+0∗L=L2W′(t)=LW′(t)
将公式 (2)代入公式(5)中,可以得到:
P ′ ( t ) = W ′ ( t ) L = b W ( t ) L ( 1 − W ( t ) L ) = b P ( t ) ( 1 − P ( t ) ) \begin{align} P^{'}(t)&=\frac{W^{'}(t)}{L} \newline&=\frac{bW(t)}{L}(1-\frac{W(t)}{L}) \newline&= bP(t)(1-P(t)) \end{align} P′(t)=LW′(t)=LbW(t)(1−LW(t))=bP(t)(1−P(t))
P ′ ( t ) = b P ( t ) ( 1 − P ( t ) ) P'(t)=bP(t)(1-P(t)) P′(t)=bP(t)(1−P(t)),这是一个一阶自治微分方程,导数是自身的函数,结合前面 逻辑回归(上):函数求导过程自推 LaTex 语法 的推导结果,可知,这里 P(t) 就是逻辑回归函数:
g ( z ) = 1 1 + e − z g(z)=\frac{1}{1+e^{-z}} g(z)=1+e−z1
模型含义
意义:当一个物种迁入到一个新生态系统中后,其数量会发生变化。假设该物种的起始数量小于环境的最大容纳量,则数量会增长。该物种在此生态系统中有天敌、食物、空间等资源也不足(非理想环境),则增长函数满足逻辑斯谛方程,图像呈S形,此方程是描述在资源有限的条件下种群增长规律的一个最佳数学模型。
相关文章:

逻辑回归(下): Sigmoid 函数的发展历史
背景 闲来无事翻了一下之前买的一个机器学习课程及之前记录的网络笔记,发现遇到公式都是截图,甚至是在纸上用笔推导的。重新整理一遍之前逻辑回归函数的学习笔记,主要是为了玩一下 LaTex 语法,写公式挺有意思的。 整理之前三篇笔…...
——RabbitMQ 各种交换机的区别与应用)
快速理解mQ(三)——RabbitMQ 各种交换机的区别与应用
RabbitMQ是一个开源的消息代理软件,它实现了高级消息队列协议(AMQP),允许应用程序或系统以异步的方式交换数据。RabbitMQ中的交换机(Exchange)是消息的分发中心,它接收来自生产者的消息…...

【五分钟学会】YOLO11 自定义数据集从训练到部署
数据集地址 数据集包含 360 张红血细胞图像及其注释文件,分为训练集与验证集。训练文件夹包含 300 张带有注释的图像。测试和验证文件夹都包含 60 张带有注释的图像。我们对原始数据集进行了一些修改以准备此 CBC 数据集,并将数据集分成三部分。在360张…...

Redis学习(十二)连接数不足报错及分析修复:ERR max number of clients reached.
目录 一、问题介绍二、问题分析2.1 redis-cli 登录2.2 info clients 查看连接数情况2.3 client list 查看具体连接情况2.4 分析连接空闲时长2.5 client list 根据客户端IP统计连接数 三、问题结论和解决3.1 问题结论:3.2 解决方案①:优化程序3.3 解决方案…...
)
八股文面试题总结(包含主流的面试经典题)
Java基础 1、JDK和JRE的区别是什么** JDK是Java开发工具包,JRE是Java运行时环境,二者的区别在于 JRE是Java程序运行所必须的,它包含jvm和一些Java的基础类库 JDK是Java程序开发所必须的,它包含JRE和一些开发工具 总结一下就是…...

一分钟掌握 Java22 新特性
1. 增强的模式匹配(Pattern Matching for Switch) Java 22 扩展了模式匹配的功能,允许在 switch 语句中使用模式匹配,从而使代码更加简洁和易读。 示例代码: public class PatternMatchingSwitchDemo {public stati…...

西安凭借入驻企业展示科技“硬”实力的数字媒体产业园
在古城西安的怀抱中,一座以科技“硬”实力为核心竞争力的数字媒体产业园——西安国际数字影像产业园,正以其独特的魅力和无限的潜力,吸引着全球的目光。这里,不仅是数字创意的孵化场,更是科技创新的策源地。 西安国际数…...
【网络安全】利用XSS、OAuth配置错误实现token窃取及账户接管 (ATO)
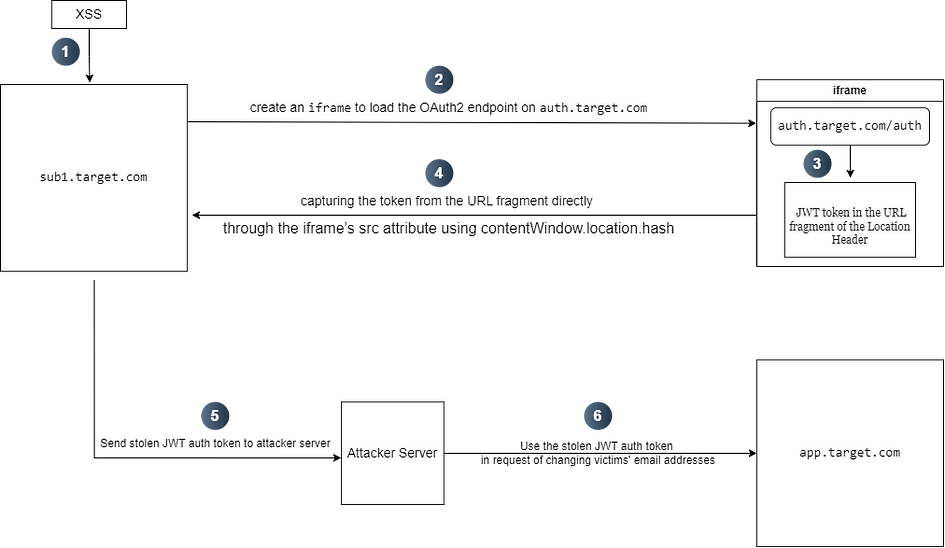
未经许可,不得转载。 文章目录 正文正文 目标:target.com 在子域sub1.target.com上,我发现了一个XSS漏洞。由于针对该子域的漏洞悬赏较低,我希望通过此漏洞将攻击升级至app.target.com,因为该子域的悬赏更高。 分析认证机制后,我发现: sub1.target.com:使用基于Cook…...

浙江所有省级医院体检报告查询上线浙里办!
在医院完成体检后不知道什么时候出报告 体检报告出来后又要跑一次医院去拿报告 历年体检报告没保管好 往年体检报告找不到了 ………… 编辑 为解决这些问题,浙江省卫生健康委结合“两卡融合、一网通办”工作的推进,不断丰富电子健康医保卡的功能&#…...

支付宝支付Java+uniapp支付宝小程序
JS: request.post(/vip/pay, {//这是自己写的java支付接口id: this.vipInfo.id,payWay: alipay-mini}).then((res) > {let success (res2) > {//前端的支付成功回调函数this.$refs.popup.close();// 支付成功刷新当前页面setTimeout(() > {this.doGetVipI…...

Linux-磁盘优化的几个思路
优化前先看看性能指标 I/O 基准测试 fio(Flexible I/O Tester)正是最常用的文件系统和磁盘 I/O 性能基准测试工具。这类工具非常用,了解即可 应用程序优化 应用程序处于整个 I/O 栈的最上端,它可以通过系统调用,来调…...

【第三版 系统集成项目管理工程师】第15章 组织保障
持续更新。。。。。。。。。。。。。。。 【第三版】第十五章 组织保障 15.1信息和文档管理15.1.1 信息和文档1.信息系统信息-P5462.信息系统文档-P546 15.1.2 信息(文档)管理规则和方法1.信息(文档)编制规范-P5472.信息(文档)定级保护-P5483.信息(文档)配置管理-P549练习 15.…...

从编程视角看生命、爱、自由、生活的排列顺序
从编程视角看生命、爱、自由、生活的排列顺序 离开大学校园,踏入大厂成为一名算法工程师后,我常以编程思维看待生活中的事物。在思考生命、爱、自由和生活的排列顺序时,发现从编程角度分析这些概念会有独特见解。 一、生命——程序的核心代…...

Lumerical——属性编辑窗口的详解
一、几何选项卡(Geometry tab) 通过几何选项卡中的选项可以设定物件的位置和大小。 二、材料选项卡(Material tab) ① 材料(MATERIAL): 在该字段可以设置成材料数据库中包含的任何材料。数据库也有可能包含一些新材料,也可以对已经包含的材料进行编辑。如果选…...
思路解析)
08实战篇:972应用题(2024)思路解析
在本节中,你将学习到: 2024年972应用题的基本解题思路如何应对陌生的社会/学术热点问题,避免初见杀题目一:阐述搜索引擎的工作基本原理 关键词:搜索引擎、基本原理题型:基础概念题这是一道混在应用题中的简答题。根据《信息检索》一书中的P37内容回答即可(同时对应P45—…...

解决应用程序启动失败问题:由于找不到d3dx9_43.dll文件,如何快速有效地恢复和修复缺失的DLL组件
由于找不到d3dx9_43.dll,许多用户在启动某些游戏或者图形相关软件时遇到了棘手的问题。这个小小的DLL文件,虽然看似不起眼,却在众多基于DirectX 9技术构建的应用程序中扮演着至关重要的角色。对于游戏爱好者来说,当满心欢喜地准备…...

Ubuntu——双系统Ubuntu22.04系统安装和基础配置
文章目录 一、Ubuntu22.04双系统安装双系统安装和卸载 二、基础配置更新软件源搜狗输入法TimeShift上网 三、AI配置CondaCUDA12.6Pytorch2.3.0-cu121 四、额外配置Samba局域网文件共享系统 一、Ubuntu22.04双系统安装 双系统安装和卸载 双系统卸载安装Ubuntu双系统windows系统…...

stm32定时器中断和外部中断
一,中断系统的介绍 中断:在主程序运行过程中,出现了特定的中断触发条件(中断源),使得CPU暂停当前正在运行的程序,转而去处理中断程序,处理完成后又返回原来被暂停的位置继续运行 中…...

LeetCode 每日一题 2024/9/30-2024/10/6
记录了初步解题思路 以及本地实现代码;并不一定为最优 也希望大家能一起探讨 一起进步 目录 9/30 1845. 座位预约管理系统10/1 983. 最低票价10/2 1870. 准时到达的列车最小时速10/3 1928. 规定时间内到达终点的最小花费10/4 1227. 飞机座位分配概率10/5 2187. 完成…...
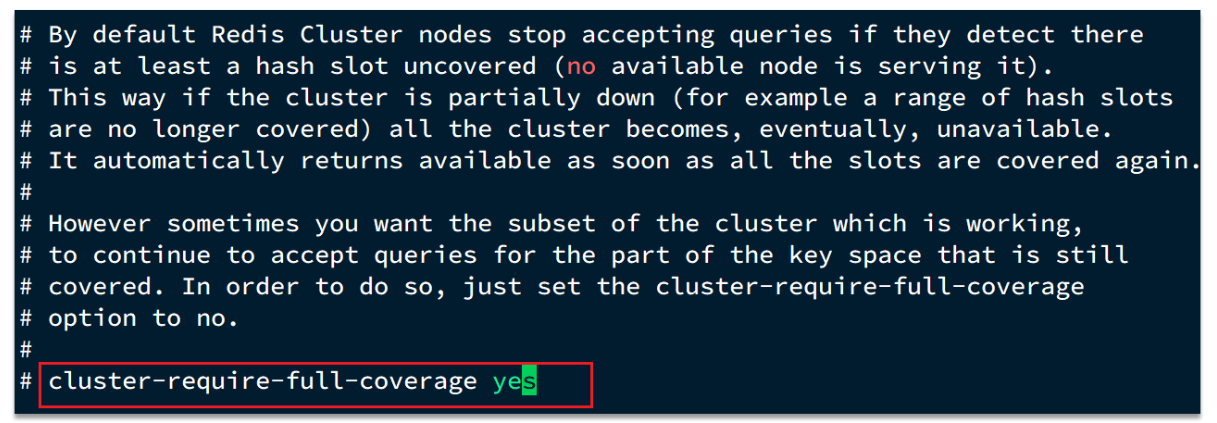
Redis篇(最佳实践)(持续更新迭代)
介绍一:键值设计 一、优雅的key结构 Redis 的 Key 虽然可以自定义,但最好遵循下面的几个最佳实践约定: 遵循基本格式:[业务名称]:[数据名]:[id]长度不超过 44 字节不包含特殊字符 例如: 我们的登录业务࿰…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

Python爬虫实战:研究MechanicalSoup库相关技术
一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库,专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力,提供了直观的 API,让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...
