初识Mysql/备份,基础指令
1,MySQL登录指令:
mysql -h 127.0.0.1 -P3306 -u -p
其中,-h指明登录部署了mysql服务的主机
-P指明要访问的端口号,
-u指明登录用户
-p输入密码
2,数据库基础
mysql:表示的是客户端
mysqld:表示的是服务端
1,理论知识
mysql它是数据库服务的客户端
mysql的本质是基于CS的一种网络服务
mysql是一套给我提供数据存取的服务的网络程序
数据库一般指的是在磁盘或者内存中存储特定结构组织的数据
2,为什么要用mysql存储数据?
基于我们现在对Linux的理解,知道一般的文件也是可以提供数据存储功能,但我们从用户的角度来讲,文件并没有很好的数据管理能力,这时候mysql的作用就体现在这里,可以对数据进行有效的管理。
所以mysql本质:对数据内容存储的一套解决方案,你给我字段或者要求,我直接给你结果就行。
3,结合一切皆文件来理解mysql
我们知道,mysql也是数据,在Linux下也是文件的一部分,那么mysql存储的数据也是文件的一部分,那么这些文件存在哪了?如下图中show databases;中的数据:

我们可以去配置文件:my.cnf中找数据库的村粗路径:(vim etc/my.cnf)

我们可以看到,datadir这个地方后面跟的路径,就是数据存储的默认位置

可以看到。我们创建的一个数据库:helloworld在Linux文件下是一个目录,,进而可以知道我们创建的数据库其实被管理在一个磁盘单中。
4,基础指令
关键字:create database +name可以创建一个数据库
如何建表:
use +数据库名字选定要建表的数据库,
再用指令:create table +name(age int,
name varchar(32)); 等可以创建一个表:

如何向表里插入数据:
用指令insert into +表名(表中定义的类型) values(+内容)
例:

如何查看表数据:
使用use+数据库名字
再使用show * from + 表名:

就可以查看表的内容。
如何删除库:
指令:drop database + 表名可以直接删除数据库
但是我不建议直接删除,删除之前要注意做好数据备份,删去就什么都没了。
用create database或者table时候可以加上 if not exists来看文件是否存在。
5,数据库编码初识
1,数据库编码集 -- 数据库存储数据的编码
2,数据库效验集--支持的数据库编码
可以用指令:show variables like ’character_set_database';查看:

可以看到我的系统是默认使用utf8
如何修改库的编码集?
指令:alter database +name charset=“ xxx” collate + 效验;
6,备份
mysqldump -P 3306 -uroot -p -B +name > name.sql
:上面操作相当于把历史操作备份了
再删除再导入:
source+路径就可以回复数据库:





可以看到数据库恢复成功。
希望能对大家有所帮助
相关文章:

初识Mysql/备份,基础指令
1,MySQL登录指令: mysql -h 127.0.0.1 -P3306 -u -p 其中,-h指明登录部署了mysql服务的主机 -P指明要访问的端口号, -u指明登录用户 -p输入密码 2,数据库基础 mysql:表示的是客户端 mysqld&…...
没想到吧!线稿上色居然可以这么简单
前言 在创意无限的数字艺术世界里,艺术创作中的线稿上色,向来是件既费时又需技巧的活儿,寻找一款既能激发灵感又能简化繁琐流程的工具,是每位艺术家心中的向往。 今天,为大家推荐一款革命性的线稿上色AI工具——千鹿…...

修改Docker的默认存储路径
docker默认存储路径:/var/lib/docker/ 执行 docker info 查看,得到以下信息 Docker Root Dir: /var/lib/docker/Debug Mode: falseRegistry: https://index.docker.io/v1/Labels:Experimental: falseInsecure Registries: 1.修改docker配置 要修改默认…...
深入计算机语言之C++:C到C++的过度
🔑🔑博客主页:阿客不是客 🍓🍓系列专栏:从C语言到C语言的渐深学习 欢迎来到泊舟小课堂 😘博客制作不易欢迎各位👍点赞⭐收藏➕关注 一、什么是C C(c plus plusÿ…...

HR面试篇
一.面试中被问职业规划 HR感兴趣的不是你的职业规划,感兴趣的是你的职业规划和他们公司有没有关系。 或者说他们公司能不能去帮助你去实现你的职业规划。 切忌不要讲不合实际的,比如要在公司赚多少钱等等。 要根据公司的特点,找到切入点,只要讲得积极向上就可以。 二.…...
深度探索Kali Linux的精髓与实践应用
Kali Linux简介 Kali Linux作为全球网络安全领域的首选操作系统之一,其强大的功能性及广泛的适用范围令人瞩目。除了上述基础介绍外,让我们深入探究Kali Linux的几个关键特性及其在实际操作中的具体应用案例。 Kali工具集成:全面的安全工具…...
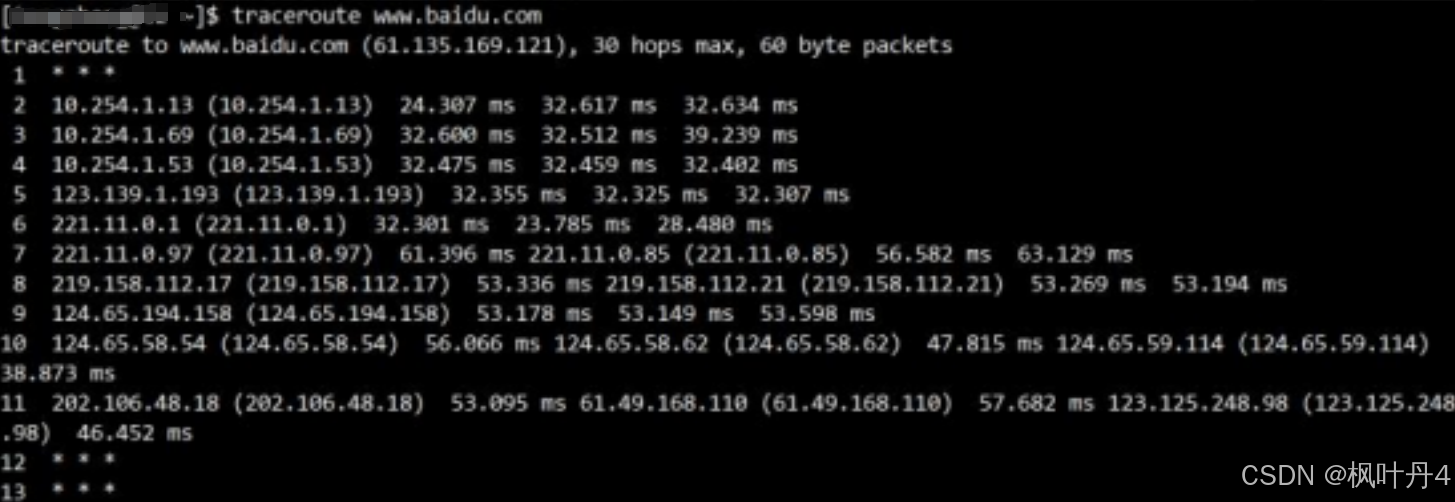
【在Linux世界中追寻伟大的One Piece】DNS与ICMP
目录 1 -> DNS(Domain Name System) 1.1 -> DNS背景 2 -> 域名简介 2.1 -> 域名解析过程 3 -> 使用dig工具分析DNS 4 -> ICMP协议 4.1 -> ICMP功能 4.2 -> ICMP报文格式 4.3 -> Ping命令 4.4 -> traceroute命令 1 -> DNS(Domain Na…...

信息安全工程师(41)VPN概述
前言 VPN,即Virtual Private Network(虚拟专用网络)的缩写,是一种通过公共网络(如互联网)创建私密连接的技术。 一、定义与工作原理 定义:VPN是依靠ISP(Internet Service Provider&…...

算法:双指针系列(一)
双指针系列 一、移动零(一)题目分析(二)代码展示二、复写零(一)题目分析(二)代码展示三、快乐数(一)题目分析(二)代码展示(…...

跟《经济学人》学英文:2024年09月28日这期 The curse of the Michelin star
The curse of the Michelin star Restaurants awarded the honour are more likely to close, research finds 原文: The twelve new restaurants added to the New York Michelin Guide this month, serving up cuisine ranging from “haute French” to “eco…...

Java Set 的介绍与实现原理
什么是 Set 在 Java 中,Set 是一种集合类型,它不允许重复的元素。Set 接口是 Java Collections Framework 的一部分,主要用于存储不重复的值。常见的实现类包括 HashSet、LinkedHashSet 和 TreeSet。 实现原理 1. HashSet HashSet 是最常…...

我谈均值平滑模板——给均值平滑模板上升理论高度
均值平滑(Mean Smoothing),也称为盒状滤波(Box Filter),通过计算一个像素及其周围像素的平均值来替换该像素的原始值,从而达到平滑图像的效果。 均值平滑通常使用一个模板(或称为卷…...

WordPress添加https协议致使后台打不开解决方法
由于删除WordPress缓存插件后操作不当,在加上升级处理,致使茹莱神兽博客的首页出现了https不兼容问题,WordPress后台也无法登陆,链接被误认为是定向重置次数过多,在网上找了好久的答案。 还有就是求助了好些人…...

如何使用pymysql和psycopg2执行SQL语句
在Python中,pymysql和psycopg2是两个非常流行的库,用于与MySQL和PostgreSQL数据库进行交互。本文将详细介绍如何使用这两个库来执行SQL查询、插入、更新和删除操作。 1. 准备工作 首先,确保已经安装了pymysql和psycopg2库。如果尚未安装&a…...

linux无法使用ll命令
ll命令是ls -l的别名,无法使用通常是该用户没有该别名配置,只需要简单添加即可使用 修改~/.bashrc # 备份 cp ~/.bashrc ~/.bashrc.source # 编辑 vim ~/.bashrc添加如下内容 # 别名 alias llls -l加载配置 source ~/.bashrc...

STM32输入捕获模式详解(上篇):原理、测频法与测周法
1. 前言 在嵌入式系统的开发过程中,常常需要对外部信号进行精确的时间测量,如测量脉冲信号的周期、频率以及占空比等。STM32系列微控制器提供了丰富的定时器资源,其中的输入捕获(Input Capture, IC)模式能实现对信号的…...

面试中遇到的关于Transformer模型的问题有哪些?
Transformer是深度学习中极具影响力的模型架构之一,广泛应用于自然语言处理、计算机视觉等领域。它通过自注意力机制和并行计算等特点,取得了比传统模型(如RNN、LSTM)更优异的性能。本文将针对Transformer的多个关键问题进行详细探…...

【UE】自动添加Megascans所有资产到自己的账户
1. 复制如下代码: ((async (startPage 0, autoClearConsole true) > {const getCookie (name) > {const value ; ${document.cookie};const parts value.split(; ${name});if (parts.length 2) return parts.pop().split(;).shift();}const callCacheA…...

【函数】4.函数的单调性
本节课没有笔记示例,自己做好笔记! 复合函数的单调性 最值 没讲 提醒我...
网格剖分-耳切法效果展示
1.前言 将简单多边形转换成一组由同样顶点组成的三角形集合是计算机图形学中的一个经典问题。问题中,简单多边形是指由一组有序顶点组成的,点V0~点Vn-1。相邻的顶点之间通过边(Vi,Vi-1)连接,并且边(Vn-1,V0)连接起始点…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...

Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习)
Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习) 一、Aspose.PDF 简介二、说明(⚠️仅供学习与研究使用)三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...

初探Service服务发现机制
1.Service简介 Service是将运行在一组Pod上的应用程序发布为网络服务的抽象方法。 主要功能:服务发现和负载均衡。 Service类型的包括ClusterIP类型、NodePort类型、LoadBalancer类型、ExternalName类型 2.Endpoints简介 Endpoints是一种Kubernetes资源…...
