算法思想 - 贪心算法
本文主要介绍算法中贪心算法的思想: 保证每次操作都是局部最优的,并且最后得到的结果是全局最优的。
贪心思想相关题目
分配饼干
455. Assign Cookies (Easy)
Input: [1,2], [1,2,3]
Output: 2Explanation: You have 2 children and 3 cookies. The greed factors of 2 children are 1, 2.
You have 3 cookies and their sizes are big enough to gratify all of the children,
You need to output 2.题目描述: 每个孩子都有一个满足度,每个饼干都有一个大小,只有饼干的大小大于等于一个孩子的满足度,该孩子才会获得满足。求解最多可以获得满足的孩子数量。
给一个孩子的饼干应当尽量小又能满足该孩子,这样大饼干就能拿来给满足度比较大的孩子。因为最小的孩子最容易得到满足,所以先满足最小的孩子。
证明: 假设在某次选择中,贪心策略选择给当前满足度最小的孩子分配第 m 个饼干,第 m 个饼干为可以满足该孩子的最小饼干。假设存在一种最优策略,给该孩子分配第 n 个饼干,并且 m < n。我们可以发现,经过这一轮分配,贪心策略分配后剩下的饼干一定有一个比最优策略来得大。因此在后续的分配中,贪心策略一定能满足更多的孩子。也就是说不存在比贪心策略更优的策略,即贪心策略就是最优策略。
public int findContentChildren(int[] g, int[] s) {Arrays.sort(g);Arrays.sort(s);int gi = 0, si = 0;while (gi < g.length && si < s.length) {if (g[gi] <= s[si]) {gi++;}si++;}return gi;
}不重叠的区间个数
435. Non-overlapping Intervals (Medium)
Input: [ [1,2], [1,2], [1,2] ]Output: 2Explanation: You need to remove two [1,2] to make the rest of intervals non-overlapping.Input: [ [1,2], [2,3] ]Output: 0Explanation: You don't need to remove any of the intervals since they're already non-overlapping.题目描述: 计算让一组区间不重叠所需要移除的区间个数。
计算最多能组成的不重叠区间个数,然后用区间总个数减去不重叠区间的个数。
在每次选择中,区间的结尾最为重要,选择的区间结尾越小,留给后面的区间的空间越大,那么后面能够选择的区间个数也就越大。
按区间的结尾进行排序,每次选择结尾最小,并且和前一个区间不重叠的区间。
public int eraseOverlapIntervals(Interval[] intervals) {if (intervals.length == 0) {return 0;}Arrays.sort(intervals, Comparator.comparingInt(o -> o.end));int cnt = 1;int end = intervals[0].end;for (int i = 1; i < intervals.length; i++) {if (intervals[i].start < end) {continue;}end = intervals[i].end;cnt++;}return intervals.length - cnt;
}使用 lambda 表示式创建 Comparator 会导致算法运行时间过长,如果注重运行时间,可以修改为普通创建 Comparator 语句:
Arrays.sort(intervals, new Comparator<Interval>() {@Overridepublic int compare(Interval o1, Interval o2) {return o1.end - o2.end;}
});投飞镖刺破气球
452. Minimum Number of Arrows to Burst Balloons (Medium)
Input:
[[10,16], [2,8], [1,6], [7,12]]Output:
2题目描述: 气球在一个水平数轴上摆放,可以重叠,飞镖垂直投向坐标轴,使得路径上的气球都会刺破。求解最小的投飞镖次数使所有气球都被刺破。
也是计算不重叠的区间个数,不过和 Non-overlapping Intervals 的区别在于,[1, 2] 和 [2, 3] 在本题中算是重叠区间。
public int findMinArrowShots(int[][] points) {if (points.length == 0) {return 0;}Arrays.sort(points, Comparator.comparingInt(o -> o[1]));int cnt = 1, end = points[0][1];for (int i = 1; i < points.length; i++) {if (points[i][0] <= end) {continue;}cnt++;end = points[i][1];}return cnt;
}根据身高和序号重组队列
406. Queue Reconstruction by Height(Medium)
Input:
[[7,0], [4,4], [7,1], [5,0], [6,1], [5,2]]Output:
[[5,0], [7,0], [5,2], [6,1], [4,4], [7,1]]题目描述: 一个学生用两个分量 (h, k) 描述,h 表示身高,k 表示排在前面的有 k 个学生的身高比他高或者和他一样高。
为了在每次插入操作时不影响后续的操作,身高较高的学生应该先做插入操作,否则身高较小的学生原先正确插入第 k 个位置可能会变成第 k+1 个位置。
身高降序、k 值升序,然后按排好序的顺序插入队列的第 k 个位置中。
public int[][] reconstructQueue(int[][] people) {if (people == null || people.length == 0 || people[0].length == 0) {return new int[0][0];}Arrays.sort(people, (a, b) -> (a[0] == b[0] ? a[1] - b[1] : b[0] - a[0]));List<int[]> queue = new ArrayList<>();for (int[] p : people) {queue.add(p[1], p);}return queue.toArray(new int[queue.size()][]);
}分隔字符串使同种字符出现在一起
763. Partition Labels (Medium)
Input: S = "ababcbacadefegdehijhklij"
Output: [9,7,8]
Explanation:
The partition is "ababcbaca", "defegde", "hijhklij".
This is a partition so that each letter appears in at most one part.
A partition like "ababcbacadefegde", "hijhklij" is incorrect, because it splits S into less parts.public List<Integer> partitionLabels(String S) {int[] lastIndexsOfChar = new int[26];for (int i = 0; i < S.length(); i++) {lastIndexsOfChar[char2Index(S.charAt(i))] = i;}List<Integer> partitions = new ArrayList<>();int firstIndex = 0;while (firstIndex < S.length()) {int lastIndex = firstIndex;for (int i = firstIndex; i < S.length() && i <= lastIndex; i++) {int index = lastIndexsOfChar[char2Index(S.charAt(i))];if (index > lastIndex) {lastIndex = index;}}partitions.add(lastIndex - firstIndex + 1);firstIndex = lastIndex + 1;}return partitions;
}private int char2Index(char c) {return c - 'a';
}种植花朵
605. Can Place Flowers (Easy)
Input: flowerbed = [1,0,0,0,1], n = 1
Output: True题目描述: 花朵之间至少需要一个单位的间隔,求解是否能种下 n 朵花。
public boolean canPlaceFlowers(int[] flowerbed, int n) {int len = flowerbed.length;int cnt = 0;for (int i = 0; i < len && cnt < n; i++) {if (flowerbed[i] == 1) {continue;}int pre = i == 0 ? 0 : flowerbed[i - 1];int next = i == len - 1 ? 0 : flowerbed[i + 1];if (pre == 0 && next == 0) {cnt++;flowerbed[i] = 1;}}return cnt >= n;
}判断是否为子序列
392. Is Subsequence (Medium)
s = "abc", t = "ahbgdc"
Return true.public boolean isSubsequence(String s, String t) {int index = -1;for (char c : s.toCharArray()) {index = t.indexOf(c, index + 1);if (index == -1) {return false;}}return true;
}修改一个数成为非递减数组
665. Non-decreasing Array (Easy)
Input: [4,2,3]
Output: True
Explanation: You could modify the first 4 to 1 to get a non-decreasing array.题目描述: 判断一个数组能不能只修改一个数就成为非递减数组。
在出现 nums[i] < nums[i - 1] 时,需要考虑的是应该修改数组的哪个数,使得本次修改能使 i 之前的数组成为非递减数组,并且 不影响后续的操作 。优先考虑令 nums[i - 1] = nums[i],因为如果修改 nums[i] = nums[i - 1] 的话,那么 nums[i] 这个数会变大,就有可能比 nums[i + 1] 大,从而影响了后续操作。还有一个比较特别的情况就是 nums[i] < nums[i - 2],只修改 nums[i - 1] = nums[i] 不能使数组成为非递减数组,只能修改 nums[i] = nums[i - 1]。
public boolean checkPossibility(int[] nums) {int cnt = 0;for (int i = 1; i < nums.length && cnt < 2; i++) {if (nums[i] >= nums[i - 1]) {continue;}cnt++;if (i - 2 >= 0 && nums[i - 2] > nums[i]) {nums[i] = nums[i - 1];} else {nums[i - 1] = nums[i];}}return cnt <= 1;
}股票的最大收益
122. Best Time to Buy and Sell Stock II (Easy)
题目描述: 一次股票交易包含买入和卖出,多个交易之间不能交叉进行。
对于 [a, b, c, d],如果有 a <= b <= c <= d ,那么最大收益为 d - a。而 d - a = (d - c) + (c - b) + (b - a) ,因此当访问到一个 prices[i] 且 prices[i] - prices[i-1] > 0,那么就把 prices[i] - prices[i-1] 添加到收益中,从而在局部最优的情况下也保证全局最优。
public int maxProfit(int[] prices) {int profit = 0;for (int i = 1; i < prices.length; i++) {if (prices[i] > prices[i - 1]) {profit += (prices[i] - prices[i - 1]);}}return profit;
}相关文章:

算法思想 - 贪心算法
本文主要介绍算法中贪心算法的思想: 保证每次操作都是局部最优的,并且最后得到的结果是全局最优的。贪心思想相关题目分配饼干455. Assign Cookies (Easy)Input: [1,2], [1,2,3] Output: 2Explanation: You have 2 children and 3 cookies. The greed factors of 2 …...
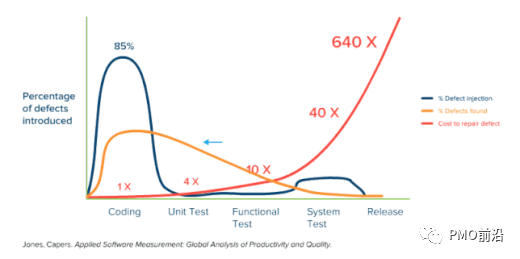
解决需求变更难题的8大方案
需求变更8大原因为什么会出现需求变更,这是由于需求约束、规则有了新的变化、由于政策发生变化,客户、沟通方式、流程化、标准化的问题等导致。这里在在过去的项目经验中,提出了常见的8大需求变更的原因。政策发生变化:指由于国家…...
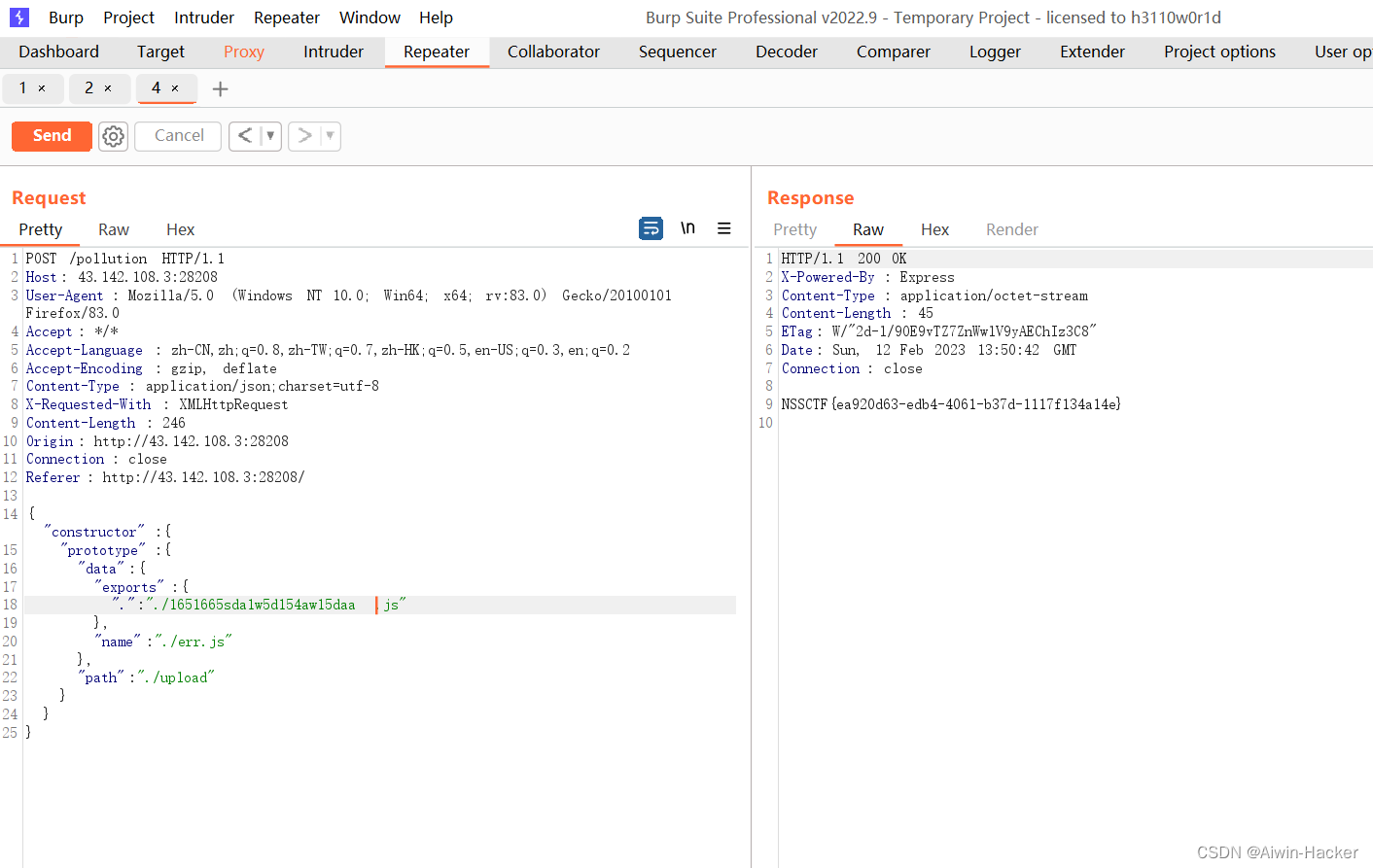
NSSROUND#8[Basic]
文章目录一、[NSSRound#8 Basic]MyDoor二、[NSSRound#8 Basic]Upload_gogoggo三、[NSSRound#8 Basic]MyPage四、[NSSRound#8 Basic]ez_node一、[NSSRound#8 Basic]MyDoor <?php error_reporting(0);if (isset($_GET[N_S.S])) {eval($_GET[N_S.S]); }if(!isset($_GET[file])…...
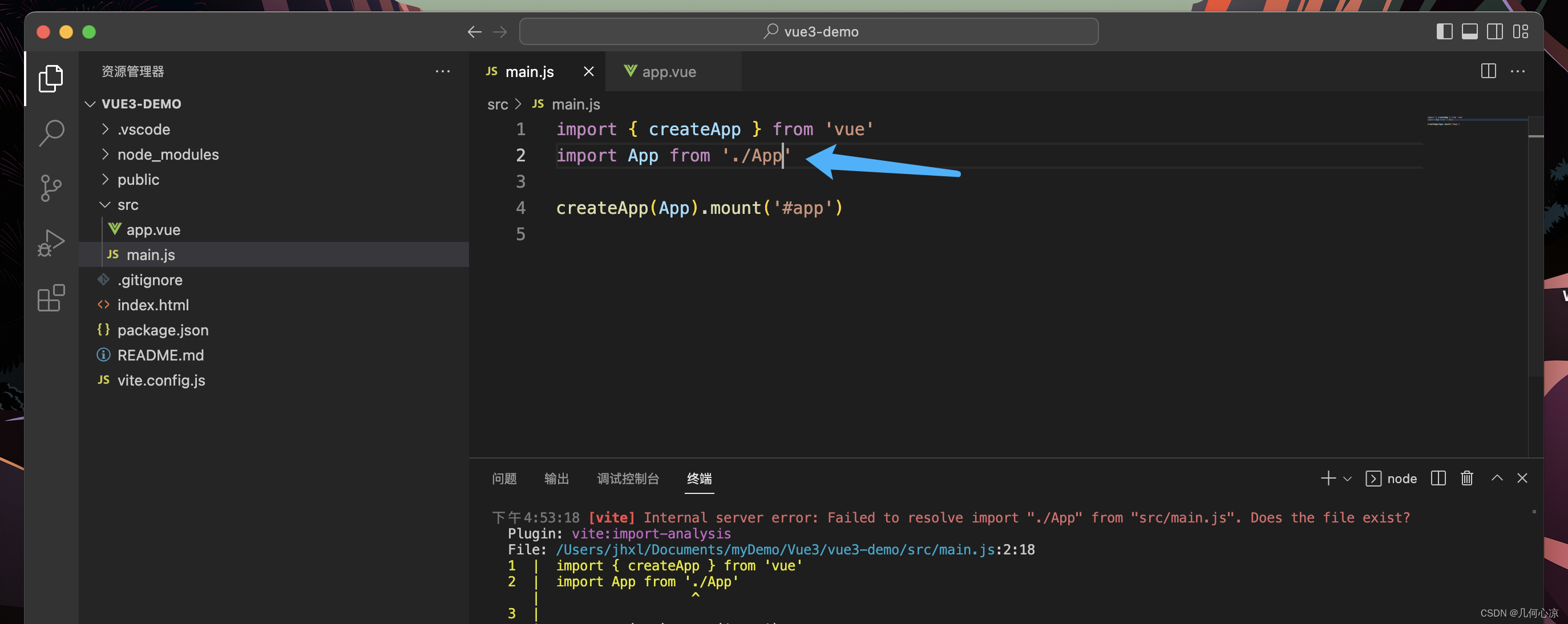
Vue3代码初体验找不同
文章目录🌟 写在前面🌟 代码分析🌟 写在最后🌟 写在前面 专栏介绍: 凉哥作为 Vue 的忠实 粉丝输出过大量的 Vue 文章,应粉丝要求开始更新 Vue3 的相关技术文章,Vue 框架目前的地位大家应该都晓…...

opencv调取摄像头录制
大家好,我是csdn的博主:lqj_本人 这是我的个人博客主页: lqj_本人的博客_CSDN博客-微信小程序,前端,python领域博主lqj_本人擅长微信小程序,前端,python,等方面的知识https://blog.csdn.net/lbcyllqj?spm1011.2415.3001.5343哔哩哔哩欢迎关注…...
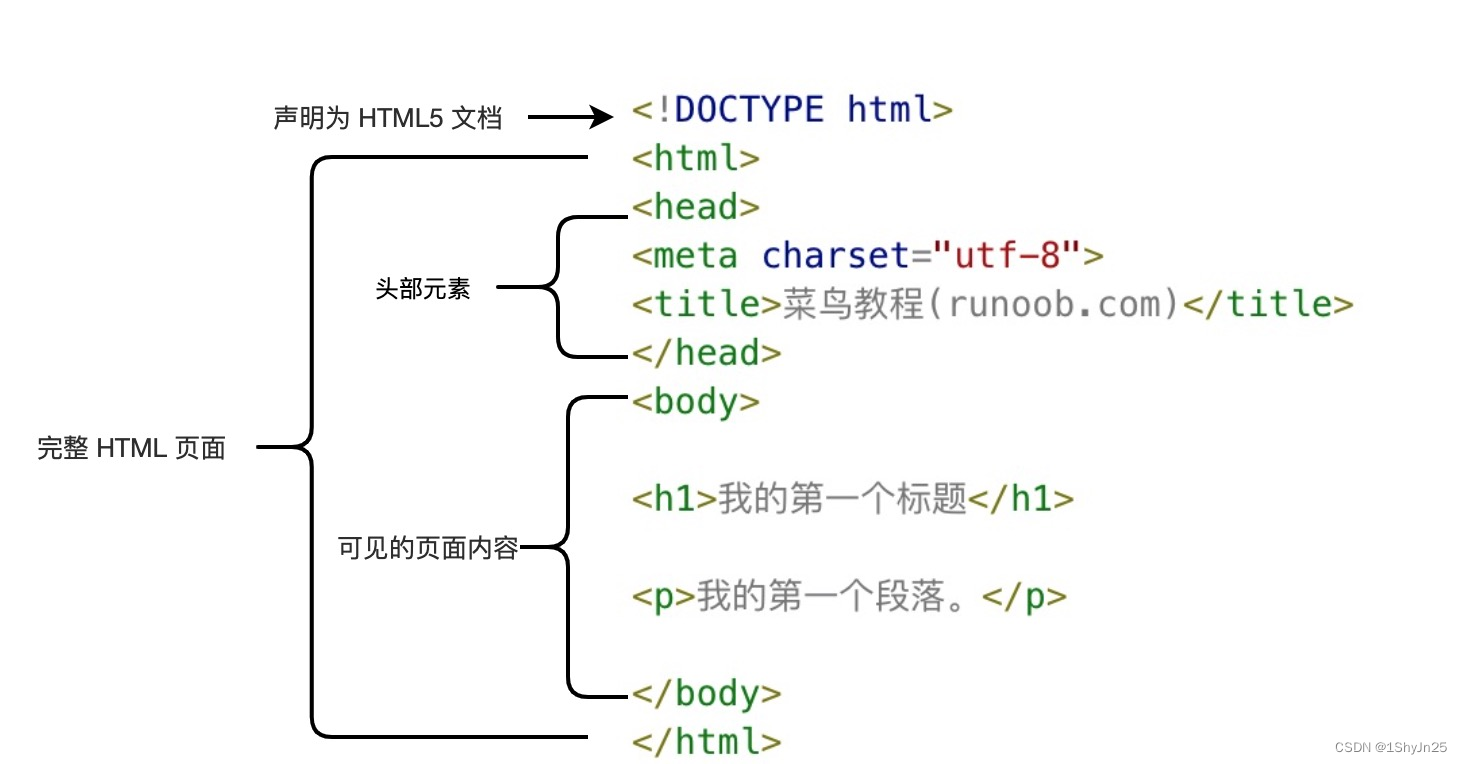
html标签手册
完整的HTML页面📑 ①基础标签📑📑📑 HTML <!DOCTYPE> 声明 !DOCTYPE声明必须是 HTML 文档的第一行,位于 html标签之前。 !DOCTYPE 声明不是 HTML 标签;它是指示 web 浏览器关于页面使用哪个 HTML 版…...
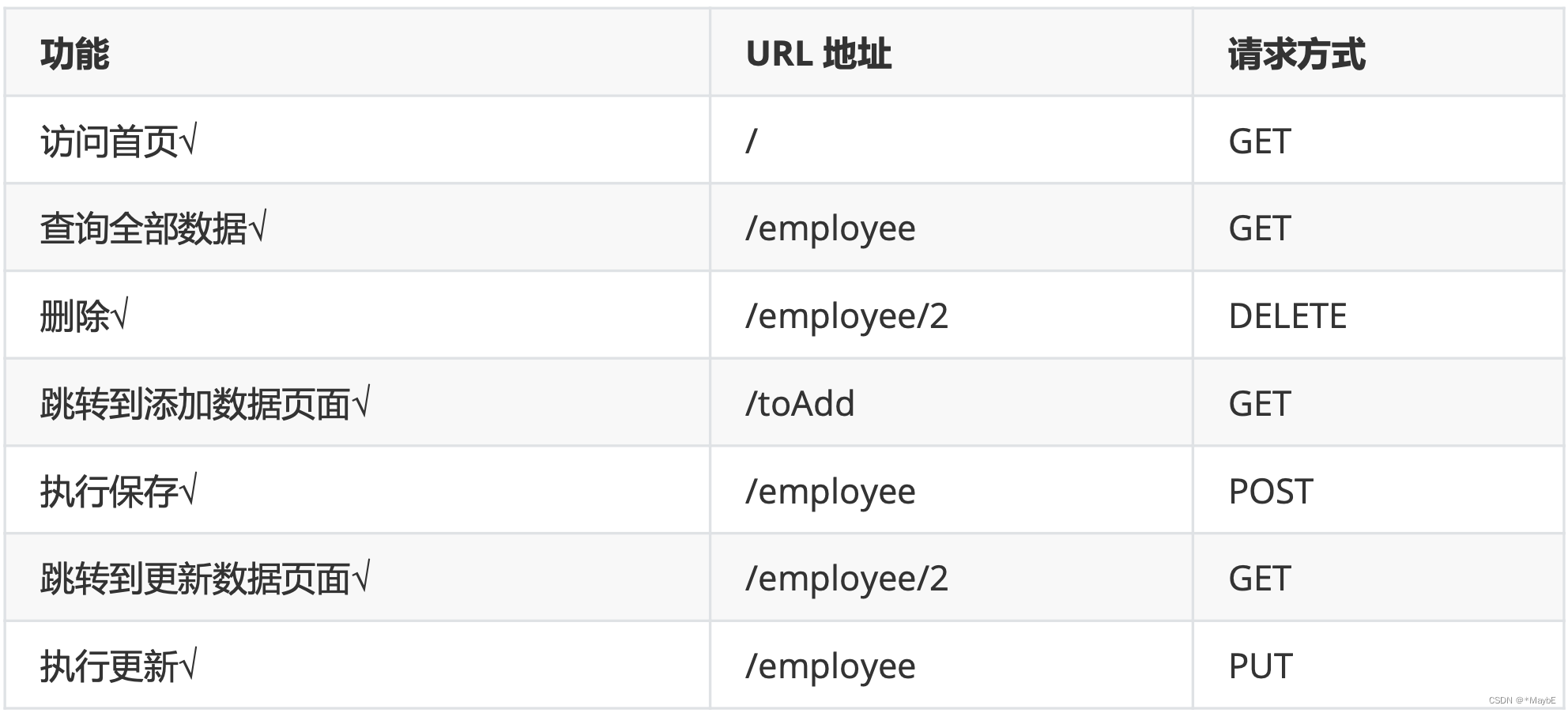
SpringMVC--视图、RESTful案例、处理AJAX请求
SpringMVC的视图 SpringMVC中的视图是View接口,视图的作用渲染数据,将模型Model中的数据展示给用户 SpringMVC视图的种类很多,默认有转发视图和重定向视图 当工程引入jstl的依赖,转发视图会自动转换为JstlView 若使用的视图技术为…...

一个同学升了leader,今年活还没干,他就已经想好组里成员的两次绩效考核怎么打了,还说:leader都是这样的!...
绩效是大家都比较关注的事情,那么作为领导,一般是怎么打绩效的呢?一位网友爆料:一个大学同学升了leader,前段时间跟他吃饭,他说他已经想好了今年组里成员的两次绩效考核怎么打了。该网友有点吃惊࿰…...
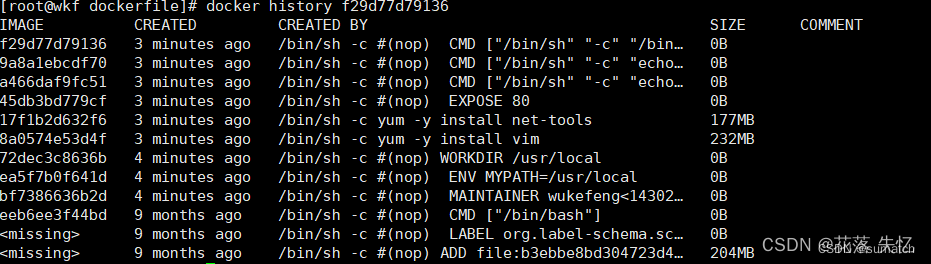
Docker 面试知识点
Docker 是什么? 是实现容器技术的一种工具是一个开源的应用容器引擎使用 C/S 架构模式,通过远程API 来管理 (我们本机是 C,docker 引擎是 S,实际的构建过程是在 docker 引擎下完成的)可以打包一个应用及依赖包到一个轻量级、可移植的容器中 …...

C++高级篇学习笔记
文章目录 前言 本文记录C一些面试难点问题剖析。 1. 左右值和右值引用的作用 左值:可以在左边,表达式结束后依然存在的持久对象,一般有名字,可以取地址。 提示: 前置自加/自减 可以做左值; 右值在右边&a…...

gentoo基本安装过程
该文章是本人在gentoo官方安装文档的基础上简单总结的,也是本人自己实践过的,目前本人用的就是gentoo,对于真的需要安装gentoo的朋友,建议还是参考官方文档,说的比较详细,这个可以简单看看,可以…...

【LeetCode】1234. 替换子串得到平衡字符串
1234. 替换子串得到平衡字符串 题目描述 有一个只含有 ‘Q’, ‘W’, ‘E’, ‘R’ 四种字符,且长度为 n 的字符串。 假如在该字符串中,这四个字符都恰好出现 n/4 次,那么它就是一个「平衡字符串」。 给你一个这样的字符串 s,…...

[动手写操作系统]-01-开机运行系统
文章目录 **概念和目标**概念目标理论源码概念和目标 概念 assembler: 汇编程序BIOS: BIOS(Basic Input Output System,基本输入输出系统)是个可编程的微型操作系统,用于管理计算机中的软硬件,它控制着系统的启动,系统是如何连接外部设备,怎样响应,调整相应操作,都是…...

最长回文子序列问题
最长回文子序列问题 问题描述:给你一个字符串 s ,找出其中最长的回文子序列,并返回该序列的长度。 子序列定义为:不改变剩余字符顺序的情况下,删除某些字符或者不删除任何字符形成的一个序列。 注意是子序列而不是子…...

月薪11k!从财务专员到软件测试工程师,成都校区小哥哥用三个月实现转行换岗
好久没和大家分享学员的转行经历了,或许在一些人看来他们的故事与自己无关,但同样也能引起一些人的共鸣,可以帮助到那些陷于就业焦虑的同学找到目标和方向。相仿的年龄、相同的职业、相似的压力…在转行软件测试追求更好生活的路上࿰…...
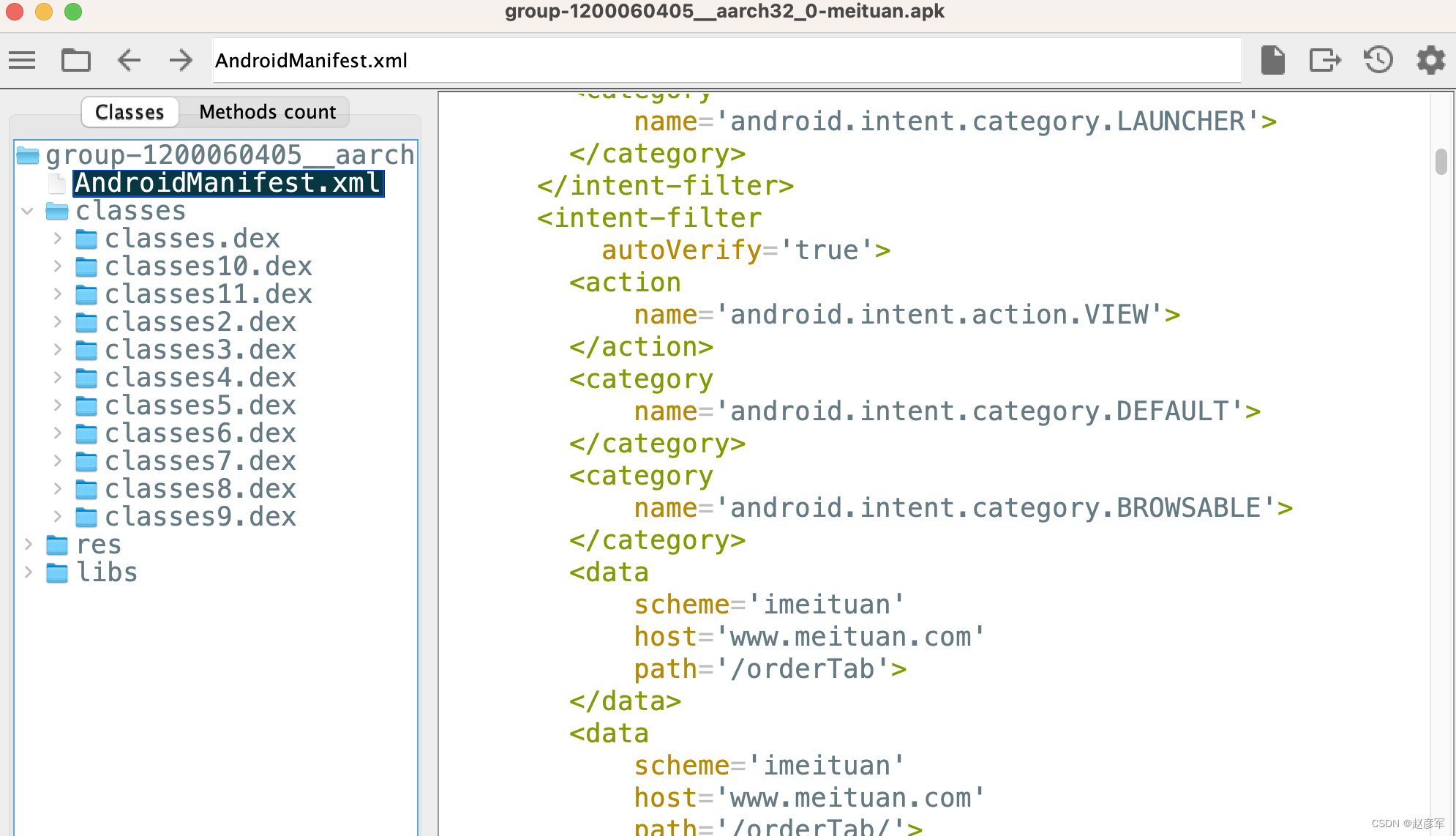
Android 逆向工具大整理,碉堡了
文章目录jadx打开 gui 界面把安装包打开双击变量名和方法名可以高亮所有出现的地方**强大的搜索功能****搜索资源****查看 APK 签名****查看 APK dex 数,方法数****查看资源,配置清单****展开包名**查找方式引用反混淆导出 Gradle 工程导出反编译资源lib…...
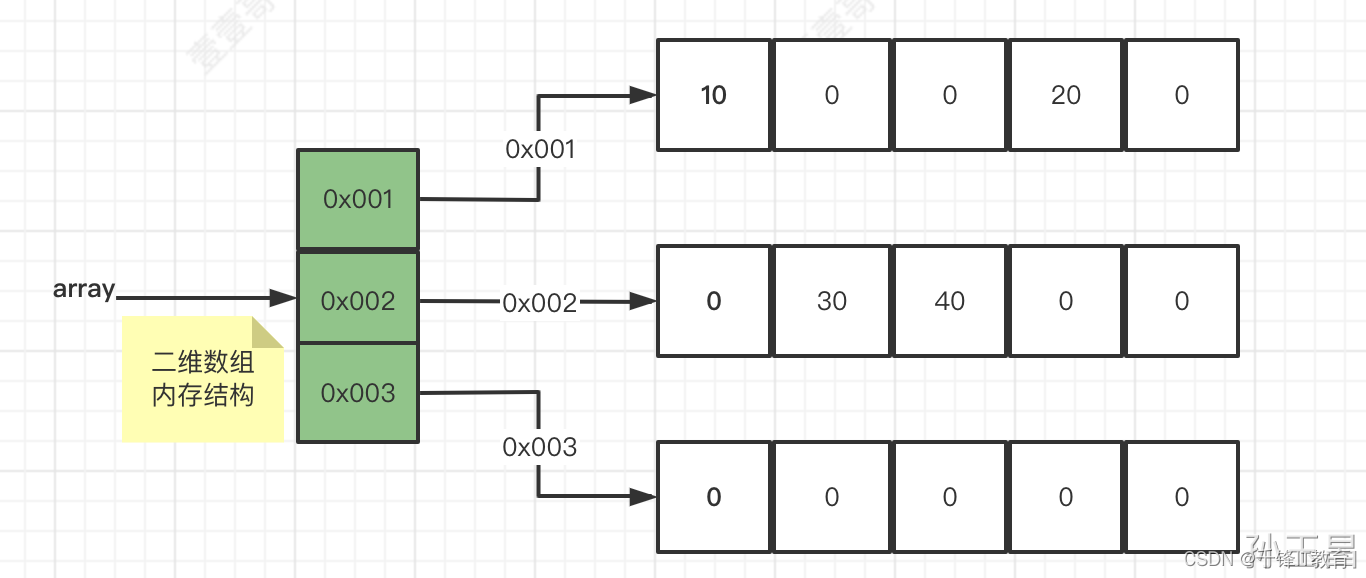
二维数组的定义
1. 概念二维数组就是一种数组的数组,其本质上还是一个一维数组,只是它的数据元素又是一个一维数组。如果你对这个概念想象不出来,给大家举个栗子,相信吸烟的同学一下子就会明白。一根烟 一个变量一包烟 20根烟 一维数组一条烟 …...

SpringMVC--获取请求参数、域对象共享数据
SpringMVC获取请求参数 通过ServletAPI获取 将HttpServletRequest作为控制器方法的形参,此时HttpServletRequest类型的参数表示封装了当前请 求的请求报文的对象 RequestMapping("/testParam") public String testParam(HttpServletRequest request){S…...

2月13日,30秒知全网,精选7个热点
///深圳支持数字经济核心区试点,市民每月免费享有1T网络流量支持基础电信企业、广电企业及互联网企业加快推进全市内容分发网络(CDN)扩容及智能改造行动,优化和完善CDN节点部署,积极利用边缘计算技术,推动互…...

【C++设计模式】学习笔记(2):模式分类与模版方法 Template Method
目录 简介模式分类GOF-23 模式分类从封装变化角度对模式分类重构获得模式 Refactoring to Patterns重构关键技法“组件协作”模式Template Method 模式动机(Motivation)结构化软件设计流程面向对象软件设计流程早绑定与晚绑定模式的定义结构(Structure)要点总结结语简介 He…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...

Python 包管理器 uv 介绍
Python 包管理器 uv 全面介绍 uv 是由 Astral(热门工具 Ruff 的开发者)推出的下一代高性能 Python 包管理器和构建工具,用 Rust 编写。它旨在解决传统工具(如 pip、virtualenv、pip-tools)的性能瓶颈,同时…...

SpringAI实战:ChatModel智能对话全解
一、引言:Spring AI 与 Chat Model 的核心价值 🚀 在 Java 生态中集成大模型能力,Spring AI 提供了高效的解决方案 🤖。其中 Chat Model 作为核心交互组件,通过标准化接口简化了与大语言模型(LLM࿰…...

基于单片机的宠物屋智能系统设计与实现(论文+源码)
本设计基于单片机的宠物屋智能系统核心是实现对宠物生活环境及状态的智能管理。系统以单片机为中枢,连接红外测温传感器,可实时精准捕捉宠物体温变化,以便及时发现健康异常;水位检测传感器时刻监测饮用水余量,防止宠物…...

EEG-fNIRS联合成像在跨频率耦合研究中的创新应用
摘要 神经影像技术对医学科学产生了深远的影响,推动了许多神经系统疾病研究的进展并改善了其诊断方法。在此背景下,基于神经血管耦合现象的多模态神经影像方法,通过融合各自优势来提供有关大脑皮层神经活动的互补信息。在这里,本研…...
