最长回文子序列问题
最长回文子序列问题
问题描述:给你一个字符串 s ,找出其中最长的回文子序列,并返回该序列的长度。
子序列定义为:不改变剩余字符顺序的情况下,删除某些字符或者不删除任何字符形成的一个序列。
注意是子序列而不是子串!
子串是连续的,比如”abda”最长回文子串就是”a”或者”b”…
子序列是不连续的,比如”abda”最长子序列就是”aba”或者”ada”
示例
输入:s = "bbbab"
输出:4
解释:一个可能的最长回文子序列为 "bbbb" 。
子序列问题本身就相对子串、子数组更困难一些,因为前者是不连续的序列,而后两者是连续的,就算穷举你都不一定会,更别说求解相关的算法问题了。
一般来说,这类问题都是让你求一个最长子序列,因为最短子序列就是一个字符。一旦涉及到子序列和最值,考察的是动态规划技巧,时间复杂度一般都是 O(n^2)。
既然要用动态规划,那就要定义 dp 数组,找状态转移关系。
1
int n = array.length;
int[] dp = new int[n];for (int i = 1; i < n; i++) {for (int j = 0; j < i; j++) {dp[i] = 最值(dp[i], dp[j] + ...)}
}
2
int n = arr.length;
int[][] dp = new dp[n][n];for (int i = 0; i < n; i++) {for (int j = 0; j < n; j++) {if (arr[i] == arr[j]) dp[i][j] = dp[i][j] + ...elsedp[i][j] = 最值(...)}
}
该文章会更新,欢迎大家批评指正。
推荐一个零声学院免费公开课程,个人觉得老师讲得不错,
分享给大家:[Linux,Nginx,ZeroMQ,MySQL,Redis,
fastdfs,MongoDB,ZK,流媒体,CDN,P2P,K8S,Docker,
TCP/IP,协程,DPDK等技术内容,点击立即学习:
服务器课程:C++服务器
相关文章:

最长回文子序列问题
最长回文子序列问题 问题描述:给你一个字符串 s ,找出其中最长的回文子序列,并返回该序列的长度。 子序列定义为:不改变剩余字符顺序的情况下,删除某些字符或者不删除任何字符形成的一个序列。 注意是子序列而不是子…...

月薪11k!从财务专员到软件测试工程师,成都校区小哥哥用三个月实现转行换岗
好久没和大家分享学员的转行经历了,或许在一些人看来他们的故事与自己无关,但同样也能引起一些人的共鸣,可以帮助到那些陷于就业焦虑的同学找到目标和方向。相仿的年龄、相同的职业、相似的压力…在转行软件测试追求更好生活的路上࿰…...
Android 逆向工具大整理,碉堡了
文章目录jadx打开 gui 界面把安装包打开双击变量名和方法名可以高亮所有出现的地方**强大的搜索功能****搜索资源****查看 APK 签名****查看 APK dex 数,方法数****查看资源,配置清单****展开包名**查找方式引用反混淆导出 Gradle 工程导出反编译资源lib…...
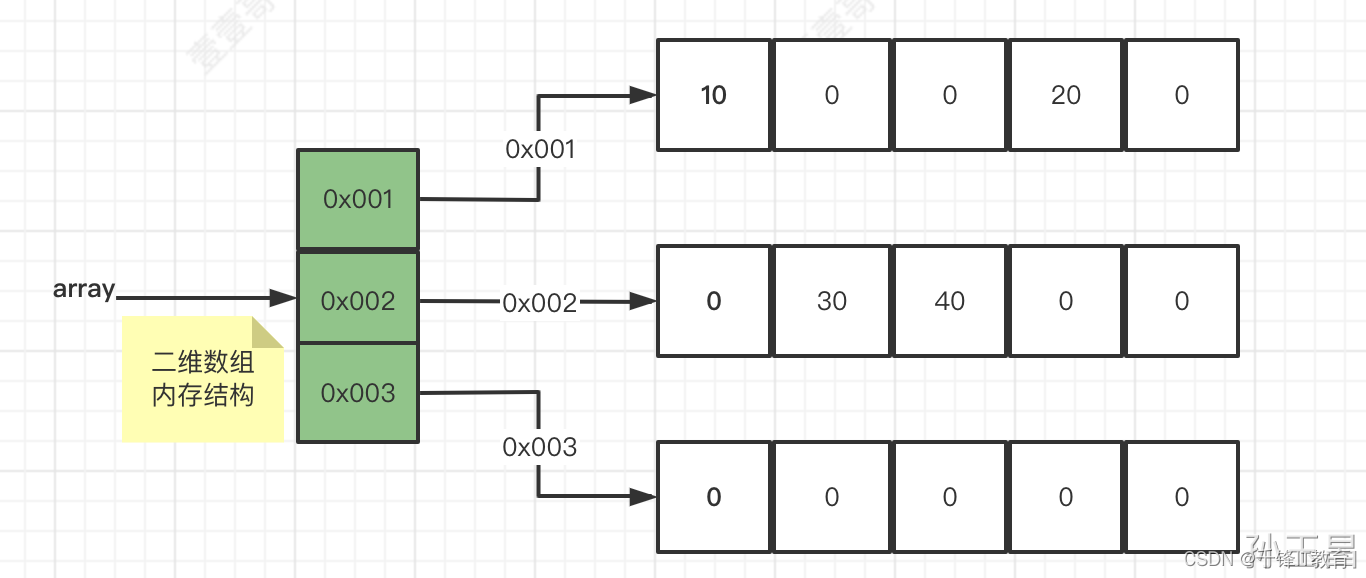
二维数组的定义
1. 概念二维数组就是一种数组的数组,其本质上还是一个一维数组,只是它的数据元素又是一个一维数组。如果你对这个概念想象不出来,给大家举个栗子,相信吸烟的同学一下子就会明白。一根烟 一个变量一包烟 20根烟 一维数组一条烟 …...

SpringMVC--获取请求参数、域对象共享数据
SpringMVC获取请求参数 通过ServletAPI获取 将HttpServletRequest作为控制器方法的形参,此时HttpServletRequest类型的参数表示封装了当前请 求的请求报文的对象 RequestMapping("/testParam") public String testParam(HttpServletRequest request){S…...

2月13日,30秒知全网,精选7个热点
///深圳支持数字经济核心区试点,市民每月免费享有1T网络流量支持基础电信企业、广电企业及互联网企业加快推进全市内容分发网络(CDN)扩容及智能改造行动,优化和完善CDN节点部署,积极利用边缘计算技术,推动互…...

【C++设计模式】学习笔记(2):模式分类与模版方法 Template Method
目录 简介模式分类GOF-23 模式分类从封装变化角度对模式分类重构获得模式 Refactoring to Patterns重构关键技法“组件协作”模式Template Method 模式动机(Motivation)结构化软件设计流程面向对象软件设计流程早绑定与晚绑定模式的定义结构(Structure)要点总结结语简介 He…...

【Swift 60秒】92 - Nil coalescing
0x00 Lesson The nil coalescing operator unwraps an optional and returns the value inside if there is one. If there isn’t a value - if the optional was nil - then a default value is used instead. Either way, the result won’t be optional: it will either b…...

python pip安装的包的路径
以ubuntu为例从一个店家那里拿到的一个ubuntu环境中,同时安装了python3.6和python2.7,又安装了ros,最后pip安装包的位置很混乱,安装的包不知道安装在了哪里。使用vscode的时候需要代码提示,就得找到包的路径࿰…...

个人收藏学习
【默认收藏夹】 CompletableFuture使用详解(全网看这一篇就行) 从头开始学MySQL-------存储过程与存储函数(4) 聊聊支付流程的设计与实现逻辑 聊聊消息中心的设计与实现逻辑 SpringBoot2 整合JTA组件,多数据源事务管理…...

【C++】类和对象---需掌握的功能
目录1.初始化列表1.1构造函数赋值1.2初始化列表格式:编译器执行的顺序:特性:1.3explicit关键字类型替换过程多参数构造函数类型替换(C11)2.static成员编程题3.匿名对象4.友元4.1友元函数4.2友元类5.内部类6.拷贝对象时…...
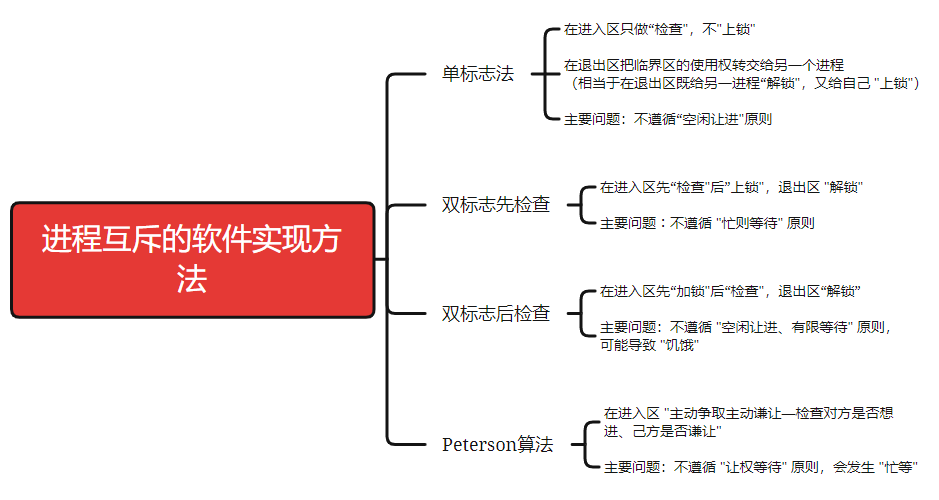
2.12、进程互斥的软件实现方法
学习提示: 理解各个算法的思想、原理结合上小节学习的 “实现互斥的四个逻辑部分”,重点理解各算法在进入区、退出区都做了什么分析各算法存在的缺陷(结合 “实现互斥要遵循的四个原则” 进行分析) 1、单标志法 算法思想:两个进…...

Java面试题-数据库
数据库相关 MySQL的索引使用 默认会有主键索引。 索引分类:单值索引、复合索引、唯一索引 详细文章 MySQL explain 分析 MySQL通过explain关键字分析SQL的执行计划。(Oracle通过EXPLAIN PLAN FOR sql) IDSELECT_TYPETABLEPARTITIONSTYPEPOSS…...
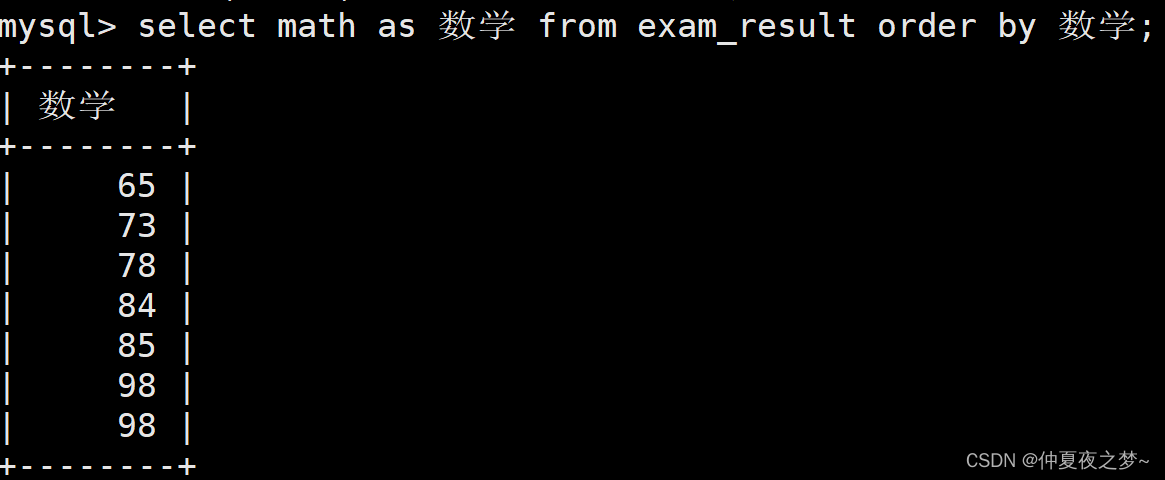
select 与 where、group by、order by、limit 子句执行优先级比较
当 select 和 其他三种语句的一者或者多者同时出现时,他们之间是存在执行先后顺序的。 他们的优先级顺序是:where > group by > select > order by > limit 目录 1、select 与 where 2、group by 与 where 、select 2、select 与 order…...
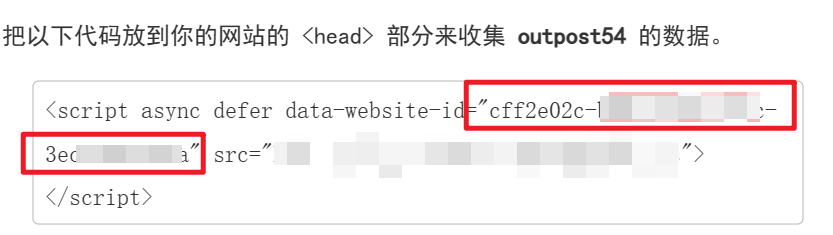
【Docker】用开源umami监控你的站点访问量
新年到,祝大家兔年吉祥!🎉 1.介绍 umami是一个开源的站点访问量监看程序,其支持docker部署到自己的服务器上。相比较百度等收费的网站信息监看,这种方式对于小站长来说更加实惠一些 2.docker安装的坑 2.1 docker-co…...
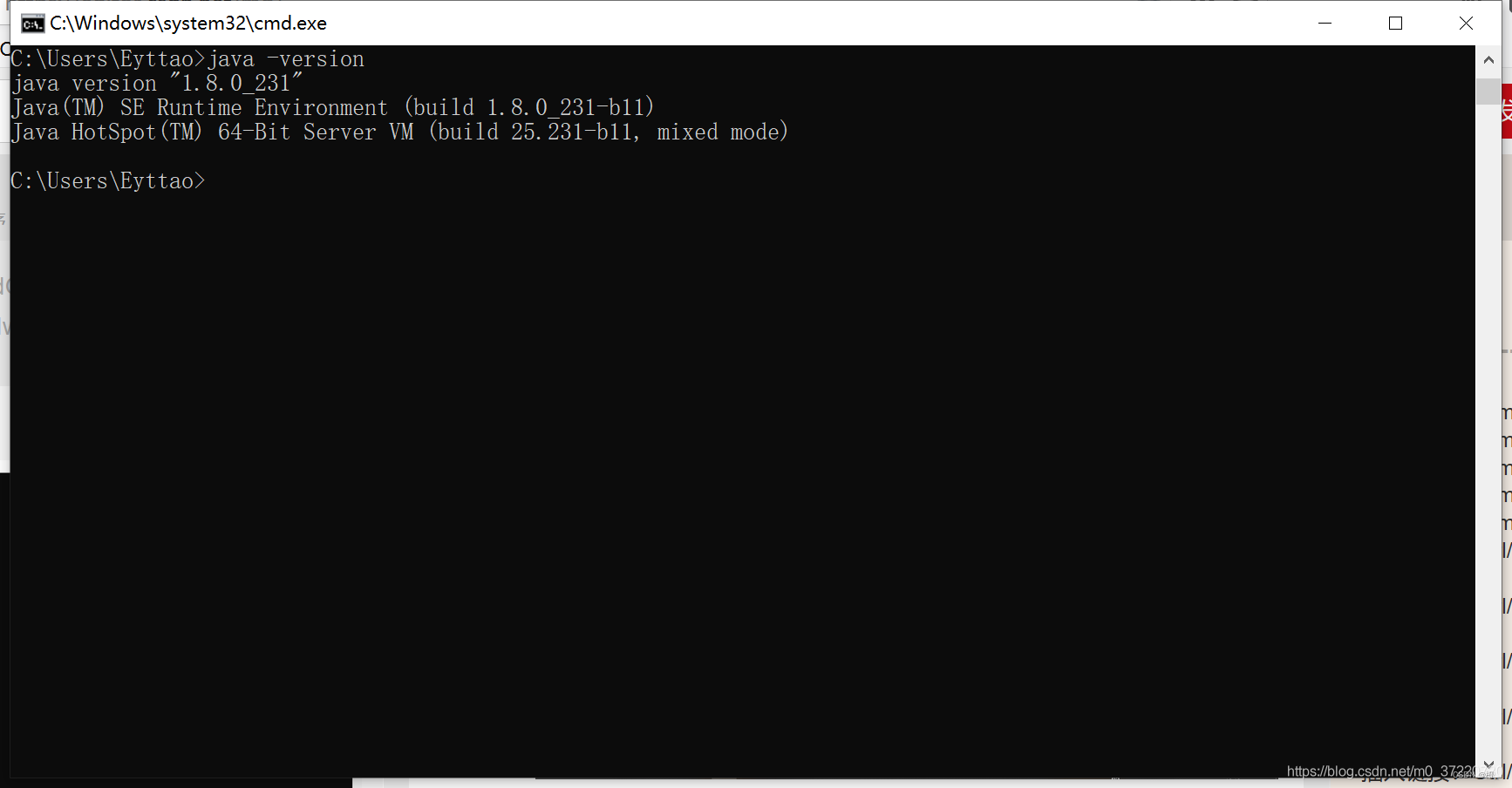
java环境配置
java环境配置步骤下载jdk安装jdk配置环境变量通过控制台命令验证配置是否成功大功告成安装教程: https://blog.csdn.net/m0_37220730/article/details/103585266 下载jdk 若不理解JDK/JRE/JVM的关系,可以点此查看初识Java(概念、版本迭代、…...

Linux系统服务:Apache安装及配置应用
目录 一、Apache安装 1、Apache简介 2、Yum安装 3、编译安装 4、服务管理 5、编译安装实现systemctl服务管理 二、Apache配置应用 1、基础应用 2、隐藏版本号 3、更改监听端口 一、Apache安装 1、Apache简介 Apache即阿帕奇是一款开源的、世界使用排名第一的Web服务…...
——背包问题)
动态规划(Dynamic Programming)——背包问题
动态规划(Dynamic Programming) 背包问题 目录动态规划(Dynamic Programming)背包问题01背包问题输入格式输出格式数据范围输入样例输出样例:二维一维完全背包问题多重背包问题输入格式输出格式数据范围输入样例输出样例:数据范围二进制优化分组背包问题…...

JVM学习02:内存结构
JVM学习02:内存结构 1. 程序计数器 1.1、定义 Program Counter Register 程序计数器(寄存器) 作用:是记住下一条jvm指令的执行地址 特点: 是线程私有的不会存在内存溢出 1.2、作用 程序计数器物理上是由寄存器来实…...
6年软件测试经验,从我自己的角度理解自动化测试
接触了不少同行,由于他们之前一直做手工测试,现在很迫切希望做自动化测试,其中不乏工作5年以上的人。 本人从事软件自动化测试已经近6年,从server端到web端,从API到mobile,切身体会到自动化带来的好处与痛楚…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...

USB Over IP专用硬件的5个特点
USB over IP技术通过将USB协议数据封装在标准TCP/IP网络数据包中,从根本上改变了USB连接。这允许客户端通过局域网或广域网远程访问和控制物理连接到服务器的USB设备(如专用硬件设备),从而消除了直接物理连接的需要。USB over IP的…...

rnn判断string中第一次出现a的下标
# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...
零知开源——STM32F103RBT6驱动 ICM20948 九轴传感器及 vofa + 上位机可视化教程
STM32F1 本教程使用零知标准板(STM32F103RBT6)通过I2C驱动ICM20948九轴传感器,实现姿态解算,并通过串口将数据实时发送至VOFA上位机进行3D可视化。代码基于开源库修改优化,适合嵌入式及物联网开发者。在基础驱动上新增…...

Oracle11g安装包
Oracle 11g安装包 适用于windows系统,64位 下载路径 oracle 11g 安装包...
