Chapter9.3:线性系统稳定性分析及综合实例
该系列博客主要讲述Matlab软件在自动控制方面的应用,如无自动控制理论基础,请先学习自动控制系列博文,该系列博客不再详细讲解自动控制理论知识。
自动控制理论基础相关链接:https://blog.csdn.net/qq_39032096/category_10287468.html?spm=1001.2014.3001.5482
博客参考书籍:《MATLAB/Simulink与控制系统仿真》。
3.线性系统稳定性分析及综合实例
李雅普诺夫理论提出了判断系统稳定性的两种方法:一种是利用线性系统微分方程的解来判断系统稳定性,称之为李雅普诺夫第一法或间接法;另一种先利用经验和技巧来构造李雅普诺夫函数,进而利用李雅普诺夫函数来判断系统稳定性,称之为李雅普诺夫第二法或直接法;
3.1 李雅普诺夫意义下的稳定性
设系统方程为:
x˙=f(x,t)\dot{x}=f(x,t) x˙=f(x,t)
式中:xxx为nnn维状态向量,且显含时间变量ttt,f(x,t)f(x,t)f(x,t)为线性或非线性、定常或时变的nnn维向量函数,其展开式为:
x˙i=fi(x1,x2,⋯,xn,t);i=1,2,⋯,n\dot{x}_i=f_i(x_1,x_2,\cdots,x_n,t);i=1,2,\cdots,n x˙i=fi(x1,x2,⋯,xn,t);i=1,2,⋯,n
假定方程的解为x(t;x0,t0)x(t;x_0,t_0)x(t;x0,t0),式中x0、t0x_0、t_0x0、t0分别为初始状态向量和初始时刻,初始条件x0x_0x0必满足x(t0;x0,t0)=x0x(t_0;x_0,t_0)=x_0x(t0;x0,t0)=x0;
-
平衡状态
对于所有ttt,满足:
x˙e=f(xe,t)=0\dot{x}_e=f(x_e,t)=0 x˙e=f(xe,t)=0
的状态xex_exe称为平衡状态;线性定常系统x˙=Ax\dot{x}=Axx˙=Ax,其平衡状态满足Axe=0Ax_e=0Axe=0,当AAA为非奇异矩阵时,系统只有唯一的零解,即只存在一个位于状态空间原点的平衡状态,若AAA为奇异矩阵,则系统存在有无穷多个平衡状态,对于非线性系统,可能有一个或多个平衡状态;
-
李雅普诺夫意义下的稳定性
设系统初始状态位于以平衡状态xex_exe为球心、δ\deltaδ为半径的闭球域S(δ)S(\delta)S(δ)内,即:
∣∣x0−xe∣∣≤δ,t=t0||x_0-x_e||≤\delta,t=t_0 ∣∣x0−xe∣∣≤δ,t=t0
若能使系统方程的解x(t;x0,t0)x(t;x_0,t_0)x(t;x0,t0)在t→∞t\to\inftyt→∞的过程中,都位于以xex_exe为球心、任意规定的半径为ε\varepsilonε的闭球域S(ε)S(\varepsilon)S(ε)内,即:
∣∣x(t;x0,t0)−x0∣∣≤ε,t≥t0||x(t;x_0,t_0)-x_0||≤\varepsilon,t≥t_0 ∣∣x(t;x0,t0)−x0∣∣≤ε,t≥t0
则称系统的平衡状态xex_exe在李雅普诺夫意义下是稳定的;式中:∣∣⋅∣∣||·||∣∣⋅∣∣为欧几里得范数,其几何意义是空间距离的尺度,如∣∣x0−xe∣∣||x_0-x_e||∣∣x0−xe∣∣表示状态空间x0x_0x0点至xex_exe点之间距离的尺度,数学表达式为:
∣∣x0−xe∣∣=(x10−x1e)2+⋯+(xn0−xne)2||x_0-x_e||=\sqrt{(x_{10}-x_{1e})^2+\cdots+(x_{n0}-x_{ne})^2} ∣∣x0−xe∣∣=(x10−x1e)2+⋯+(xn0−xne)2 -
渐近稳定性
若系统的平衡状态xex_exe不仅具有李雅普诺夫意义下的稳定性,且有:
limt→∞∣∣x(t;x0,t0)−xe∣∣=0\lim_{t\to\infty}||x(t;x_0,t_0)-x_e||=0 t→∞lim∣∣x(t;x0,t0)−xe∣∣=0
则称此平衡状态是渐近稳定的; -
大范围(全局)渐近稳定性
当初始条件扩展至整个状态空间,且平衡状态均具有渐近稳定性时,称此平衡状态是大范围渐近稳定的,此时δ→∞,S(δ)→∞\delta\to\infty,S(\delta)\to\inftyδ→∞,S(δ)→∞;当t→∞t\to\inftyt→∞时,由状态空间中任一点出发的轨迹都收敛至xxx;
对于严格线性的系统,如果它是渐近稳定的,则必定是大范围渐近稳定的,对于非线性系统来说,其稳定性与初始条件密切相关,系统渐近稳定不一定是大范围渐近稳定;
-
不稳定性
如果对于某个实数ε>0\varepsilon>0ε>0和任一个实数δ>0\delta>0δ>0,不管这两个实数有多小,在S(δ)S(\delta)S(δ)内总存在一个状态x0x_0x0,使得由这一状态出发的轨迹超出S(ε)S(\varepsilon)S(ε),则平衡状态xex_exe称为是不稳定的;
3.2 李雅普诺夫第一法(间接法)
李雅普诺夫第一法是利用状态方程解的特性来判断系统稳定性的方法,适用于线性定常、线性时变及非线性函数可线性化的情况;
定理9:对于线性定常系统x˙=Ax,x(0)=x0,t≥0\dot{x}=Ax,x(0)=x_0,t≥0x˙=Ax,x(0)=x0,t≥0,有:
- 系统的每一平衡状态是在李雅普诺夫意义下稳定的充分必要条件:AAA的所有特征值均具有非正(负或零)实部,且具有零实部的特征值为AAA的最小多项式的单根;
- 系统的唯一平衡状态xe=0x_e=0xe=0是渐近稳定的充分必要条件:AAA的所有特征值均具有负实部;
3.3 李雅普诺夫第二法(直接法)
李雅普诺夫提出,可虚构一个能量函数,被称为李雅普诺夫函数,一般它与x1,x2,⋯,xnx_1,x_2,\cdots,x_nx1,x2,⋯,xn及ttt有关,记为V(x,t)V(x,t)V(x,t);
若不显含ttt,则记为V(x)V(x)V(x);它是一个标量函数,考虑到能量总是大于零,故为正定函数;能量衰减特性用V˙(x,t)\dot{V}(x,t)V˙(x,t)或V˙(x)\dot{V}(x)V˙(x)表示;李雅普诺夫第二法用VVV及V˙\dot{V}V˙的符号特征,直接对平衡状态稳定性做出判断,无需求出系统状态方程的解;
对于线性系统,通常用二次型函数xTPxx^TPxxTPx作为李雅普诺夫函数;
-
标量函数定号性简单介绍
正定性:标量函数V(x)V(x)V(x)对所有在域SSS中的非零状态xxx有V(x)>0V(x)>0V(x)>0且V(0)=0V(0)=0V(0)=0,则在域SSS内的标量函数V(x)V(x)V(x)称为是正定的;
负定性:如果−V(x)-V(x)−V(x)是正定函数,则标量函数V(x)V(x)V(x)称为负定函数;
正半定性:如果标量函数V(x)V(x)V(x)除了原点及某些状态处等于零外,在域SSS内的所有状态都是正定的,则V(x)V(x)V(x)称为正半定函数;
负半定性:如果−V(x)-V(x)−V(x)是正半定函数,则标量函数V(x)V(x)V(x)称为负半定函数;
不定性:如果在域SSS内,不论域SSS多么小,V(x)V(x)V(x)即可为正值,也可为负值,则标量函数V(x)V(x)V(x)称为不定函数;
-
李雅普诺夫第二法主要定理
定理10(定常系统大范围渐近稳定判别定理1):对于定常系统:
x˙=f(x),t≥0\dot{x}=f(x),t≥0 x˙=f(x),t≥0
其中:f(0)=0f(0)=0f(0)=0,如果存在一个具有连续一阶导数的标量函数V(x),V(0)=0V(x),V(0)=0V(x),V(0)=0,且对于状态空间XXX中的一切非零点xxx满足如下条件:- V(x)V(x)V(x)为正定;
- V˙(x)\dot{V}(x)V˙(x)为负定;
- 当∣∣x∣∣→∞||x||\to\infty∣∣x∣∣→∞时V(x)→∞V(x)\to\inftyV(x)→∞.
则系统的原点平衡点状态是大范围渐近稳定的.
实例分析:
Example1: 设系统状态方程为:
x˙1=x2−x1(x12+x22)x˙2=−x1−x2(x12+x22)\begin{aligned} &\dot{x}_1=x_2-x_1(x_1^2+x_2^2)\\ &\dot{x}_2=-x_1-x_2(x_1^2+x_2^2) \end{aligned} x˙1=x2−x1(x12+x22)x˙2=−x1−x2(x12+x22)
确定系统的稳定性.解:
原点(x1=0,x2=0)(x_1=0,x_2=0)(x1=0,x2=0)是该系统唯一的平衡状态;
选定正定标量函数V(x)V(x)V(x)为:
V(x)=x12+x22V(x)=x_1^2+x_2^2 V(x)=x12+x22
则沿任意轨迹V(x)V(x)V(x)对时间的导数:
V˙(x)=2x1x˙1+2x2x˙2=−2(x12+x22)2\dot{V}(x)=2x_1\dot{x}_1+2x_2\dot{x}_2=-2(x_1^2+x_2^2)^2 V˙(x)=2x1x˙1+2x2x˙2=−2(x12+x22)2
是负定的.说明V(x)V(x)V(x)沿任意轨迹是连续减小的,因此V(x)V(x)V(x)是一个李雅普诺夫函数.
由于当∣∣x∣∣→∞||x||\to\infty∣∣x∣∣→∞时V(x)→∞V(x)\to\inftyV(x)→∞,所以系统在原点处的平衡状态是大范围渐近稳定的.
定理11(定常系统大范围渐近稳定判别定理2):对于定常系统,如果存在一个具有连续一阶导数的标量V(x),V(x)=0V(x),V(x)=0V(x),V(x)=0,且对状态空间XXX中的一切非零点xxx满足如下条件:
- V(x)V(x)V(x)为正定;
- V˙(x)\dot{V}(x)V˙(x)为负半定;
- 对任意x∈X,V˙(x(t;x0,0))≢0x\in{X},\dot{V}(x(t;x_0,0))\not \equiv0x∈X,V˙(x(t;x0,0))≡0;
- 当∣∣x∣∣→∞||x||\to\infty∣∣x∣∣→∞时,V(x)→∞V(x)\to\inftyV(x)→∞.
则系统的原点平衡状态是大范围渐近稳定的.
实例分析:
Example2: 已知定常系统状态方程为:
x˙1=x2x˙2=−x1−(1+x2)2x2\begin{aligned} &\dot{x}_1=x_2\\ &\dot{x}_2=-x_1-(1+x_2)^2x_2 \end{aligned} x˙1=x2x˙2=−x1−(1+x2)2x2
确定系统的稳定性.解:
原点(x1=0,x2=0)(x_1=0,x_2=0)(x1=0,x2=0)为系统唯一的平衡状态.
取V(x)=x12+x22V(x)=x_1^2+x_2^2V(x)=x12+x22,且有:
V(x)=x12+x22V(x)=x_1^2+x_2^2V(x)=x12+x22为正定,
V˙(x)=2x1x˙1+2x2x˙2=−2x22(1+x2)2\dot{V}(x)=2x_1\dot{x}_1+2x_2\dot{x}_2=-2x_2^2(1+x_2)^2V˙(x)=2x1x˙1+2x2x˙2=−2x22(1+x2)2.容易看出,除了①x1x_1x1任意,x2=0x_2=0x2=0;②x1x_1x1任意,x2=−1x_2=-1x2=−1时,V˙(x)=0\dot{V}(x)=0V˙(x)=0外,均有V˙(x)<0\dot{V}(x)<0V˙(x)<0,所以,V˙(x)\dot{V}(x)V˙(x)为负半定.
检查是否V˙(x(t;x0,0))≢0\dot{V}(x(t;x_0,0))\not\equiv0V˙(x(t;x0,0))≡0.考虑到使得V˙(x)=0\dot{V}(x)=0V˙(x)=0的可能性只有上述①和②两种情况,所有问题归结为判断这两种情况是否为系统的受扰运动解.
考察情况①:设x‾(t;x0,0)=[x1(t)0]T\overline{x}(t;x_0,0)=\begin{bmatrix}x_1(t) & 0\end{bmatrix}^Tx(t;x0,0)=[x1(t)0]T,则由x2(t)≡0x_2(t)\equiv0x2(t)≡0可导出x˙2=0\dot{x}_2=0x˙2=0,将此代入系统状态方程可得:
x˙1(t)=x2(t)=00=x˙2(t)=−(1+x2(t))2x2(t)−x1(t)=−x1(t)\begin{aligned} &\dot{x}_1(t)=x_2(t)=0\\ &0=\dot{x}_2(t)=-(1+x_2(t))^2x_2(t)-x_1(t)=-x_1(t) \end{aligned} x˙1(t)=x2(t)=00=x˙2(t)=−(1+x2(t))2x2(t)−x1(t)=−x1(t)
表明,除了点(x1=0,x2=0)(x_1=0,x_2=0)(x1=0,x2=0)外,x‾(t;x0,0)=[x1(t)0]T\overline{x}(t;x_0,0)=[x_1(t)\ \ 0]^Tx(t;x0,0)=[x1(t) 0]T不是系统的受扰运动解.考察情况②:设x‾(t;x0,0)=[x1(t)−1]T\overline{x}(t;x_0,0)=[x_1(t) \ \ \ -1]^Tx(t;x0,0)=[x1(t) −1]T,则由x2(t)=−1x_2(t)=-1x2(t)=−1可导出x˙2(t)=0\dot{x}_2(t)=0x˙2(t)=0,将此代入系统状态方程可得:
x˙1(t)=x2(t)=−10=x˙2(t)=−(1+x2(t))2x2(t)−x1(t)=−x1(t)\begin{aligned} &\dot{x}_1(t)=x_2(t)=-1\\ &0=\dot{x}_2(t)=-(1+x_2(t))^2x_2(t)-x_1(t)=-x_1(t) \end{aligned} x˙1(t)=x2(t)=−10=x˙2(t)=−(1+x2(t))2x2(t)−x1(t)=−x1(t)
这是一个矛盾的结果,表明x‾(t;x0,0)=[x1(t)−1]T\overline{x}(t;x_0,0)=[x_1(t) \ \ \ -1]^Tx(t;x0,0)=[x1(t) −1]T也不是系统受扰运动解.综合以上分析,V˙(x(t;x0,0))≢0\dot{V}(x(t;x_0,0))\not\equiv0V˙(x(t;x0,0))≡0.
当∣∣x∣∣→∞||x||\to\infty∣∣x∣∣→∞时,显然有V(x)=∣∣x∣∣2→∞V(x)=||x||^2\to\inftyV(x)=∣∣x∣∣2→∞.
因此,系统的原点平衡状态是大范围渐近稳定的.
定理12(不稳定判别定理):对于定常系统,如果存在一个具有连续一阶导数的标量函数V(x)V(x)V(x)(V(0)=0V(0)=0V(0)=0),和围绕原点的域Ω\OmegaΩ,使得对于一切x∈Ωx\in\Omegax∈Ω和一切t≥t0t≥t_0t≥t0满足如下条件:
- V(x)V(x)V(x)为正定;
- V(x)˙\dot{V(x)}V(x)˙为正定;
则系统平衡状态为不稳定.
3.4 线性定常系统的李雅普诺夫稳定性分析
-
线性定常连续系统渐近稳定性的判别
设线性定常系统状态方程为:
x˙=Ax,x(0)=x0,t≥0\dot{x}=Ax,x(0)=x_0,t≥0 x˙=Ax,x(0)=x0,t≥0
AAA为非奇异矩阵.故原点是唯一平衡状态.设取正定二次型函数V(x)=xTPxV(x)=x^TPxV(x)=xTPx作为可能的李雅普诺夫函数,考虑到系统状态方程,则有:
V˙(x)=x˙TPx+xTPx˙=xT(ATP+PA)x\dot{V}(x)=\dot{x}^TPx+x^TP\dot{x}=x^T(A^TP+PA)x V˙(x)=x˙TPx+xTPx˙=xT(ATP+PA)x
令:
ATP+PA=−Q(1)A^TP+PA=-Q\tag{1} ATP+PA=−Q(1)
有:
V˙(x)=−xTQx\dot{V}(x)=-x^TQx V˙(x)=−xTQx
线性定常连续系统渐近稳定的充分必要条件:给定一正定矩阵PPP,存在着满足式(1)(1)(1)的正定矩阵QQQ,xTPxx^TPxxTPx是该系统的一个李雅普诺夫函数,式(1)(1)(1)称为李雅普诺夫矩阵代数方程。使用中常选取QQQ阵为单位阵或对角线阵。定理13:线性定常系统x˙=Ax,x(0)=x0,t≥0\dot{x}=Ax,x(0)=x_0,t≥0x˙=Ax,x(0)=x0,t≥0的原点平衡状态xe=0x_e=0xe=0为渐近稳定的充分必要条件:对于任意给定的一个正定对称矩阵QQQ,有唯一的正定对称矩阵PPP使式(1)(1)(1)成立.
实例分析:
Example3: 已知线性定常连续系统状态方程为:
x˙1=x2,x˙2=2x1−x2\dot{x}_1=x_2,\dot{x}_2=2x_1-x_2 x˙1=x2,x˙2=2x1−x2
用李雅普诺夫方程判定系统的渐近稳定性.解:
先用特征值判据判断,系统状态方程为:
x˙=[012−1]x,A=[012−1]\dot{x}= \begin{bmatrix} 0 & 1\\ 2 & -1 \end{bmatrix}x, A= \begin{bmatrix} 0 & 1\\ 2 & -1 \end{bmatrix} x˙=[021−1]x,A=[021−1]∣λI−A∣=∣λ−1−2λ+1∣=λ2+λ−2=(λ−1)(λ+2)=0|\lambda{I}-A|= \begin{vmatrix} \lambda & -1\\ -2 & \lambda+1 \end{vmatrix}= \lambda^2+\lambda-2=(\lambda-1)(\lambda+2)=0 ∣λI−A∣=λ−2−1λ+1=λ2+λ−2=(λ−1)(λ+2)=0
特征值为:−2,1-2,1−2,1,故系统不稳定.
令:
ATP+PA=−Q=−IA^TP+PA=-Q=-I ATP+PA=−Q=−IP=PT=[P11P12P21P22]P=P^T= \begin{bmatrix} P_{11} & P_{12}\\ P_{21} & P_{22} \end{bmatrix} P=PT=[P11P21P12P22]
则有:
[021−1][P11P12P21P22]+[P11P12P21P22][012−1]=[−100−1]\begin{bmatrix} 0 & 2\\ 1 & -1 \end{bmatrix}\begin{bmatrix} P_{11} & P_{12}\\ P_{21} & P_{22} \end{bmatrix}+ \begin{bmatrix} P_{11} & P_{12}\\ P_{21} & P_{22} \end{bmatrix}\begin{bmatrix} 0 & 1\\ 2 & -1 \end{bmatrix}= \begin{bmatrix} -1 & 0\\ 0 & -1 \end{bmatrix} [012−1][P11P21P12P22]+[P11P21P12P22][021−1]=[−100−1]
展开:
4P12=−1,2P12−2P22=−1,P11−P12+2P22=04P_{12}=-1,2P_{12}-2P_{22}=-1,P_{11}-P_{12}+2P_{22}=0 4P12=−1,2P12−2P22=−1,P11−P12+2P22=0
解得:
P=[P11P12P21P22]=[−34−14−1414]P= \begin{bmatrix} P_{11} & P_{12}\\ P_{21} & P_{22} \end{bmatrix}= \begin{bmatrix} -\displaystyle\frac{3}{4} & -\displaystyle\frac{1}{4}\\ -\displaystyle\frac{1}{4} & \displaystyle\frac{1}{4} \end{bmatrix} P=[P11P21P12P22]=−43−41−4141
由于P11=−34,detP=−14<0P_{11}=-\displaystyle\frac{3}{4},\det{P}=-\displaystyle\frac{1}{4}<0P11=−43,detP=−41<0,故PPP不定,可知系统非渐近稳定.由特征值判据知系统是不稳定的. -
线性定常离散系统渐近稳定性的判别
设线性定常离散系统状态方程为:
x(k+1)=Φx(k),x(0)=x0;k=0,1,2,⋯,x(k+1)=\Phi{x}(k),x(0)=x_0;k=0,1,2,\cdots, x(k+1)=Φx(k),x(0)=x0;k=0,1,2,⋯,
式中:Φ\PhiΦ阵为非奇异;原点是平衡状态.取正定二次型函数:
V(x(k))=xT(k)Px(k)V(x(k))=x^T(k)Px(k) V(x(k))=xT(k)Px(k)
以ΔV(x(k))\Delta{V}(x(k))ΔV(x(k))代替V˙(x)\dot{V}(x)V˙(x),有:
ΔV(x(k))=V(x(k+1))−V(x(k))\Delta{V}(x(k))=V(x(k+1))-V(x(k)) ΔV(x(k))=V(x(k+1))−V(x(k))
考虑到线性定常离散系统状态方程式有:
ΔV(x(k))=xT(k)(ΦTPΦ−P)x(k)\Delta{V}(x(k))=x^T(k)(\Phi^TP\Phi-P)x(k) ΔV(x(k))=xT(k)(ΦTPΦ−P)x(k)
令:
ΦTPΦ−P=−Q(2)\Phi^TP\Phi-P=-Q\tag{2} ΦTPΦ−P=−Q(2)
有:
ΔV(x(k))=−xT(k)Qx(k)\Delta{V(x(k))}=-x^T(k)Qx(k) ΔV(x(k))=−xT(k)Qx(k)
定理14:线性定常离散系统渐近稳定的充分必要条件:给定任一正定对称矩阵QQQ,存在一个正定对称矩阵PPP使式(2)(2)(2)成立;xT(k)Px(k)x^T(k)Px(k)xT(k)Px(k)是系统的一个李雅普诺夫函数,式(2)(2)(2)称为离散的李雅普诺夫代数方程,通常可取Q=IQ=IQ=I.
如果ΔV(x(k))\Delta{V}(x(k))ΔV(x(k))沿任一解的序列不恒为零,则QQQ可取为正半定矩阵.
-
李雅普诺夫稳定性判据汇总表:

3.5 MATLAB/SIMULINK在李雅普诺夫稳定性分析中的应用
- P=lyap(A,Q){\rm P=lyap(A,Q)}P=lyap(A,Q):A{\rm A}A是已知系统的状态矩阵,Q{\rm Q}Q是给定的正定对称矩阵,P{\rm P}P是李雅普诺夫方程AP+PAT+Q=0{\rm AP+PA^T+Q=0}AP+PAT+Q=0的解,即正定实对称矩阵P{\rm P}P;
- P=lyap2(A,Q){\rm P=lyap2(A,Q)}P=lyap2(A,Q):A{\rm A}A是已知系统的状态矩阵,Q{\rm Q}Q是给定的正定对称矩阵,P{\rm P}P是李雅普诺夫方程AP+PAT+Q=0{\rm AP+PA^T+Q=0}AP+PAT+Q=0的解,即正定实对称矩阵P{\rm P}P;lyap2(){\rm lyap2()}lyap2()采用特征值分解法求解李雅普诺夫方程,运算速度比lyap(){\rm lyap()}lyap()快;
- P=dlyap(A,Q){\rm P=dlyap(A,Q)}P=dlyap(A,Q):A{\rm A}A是已知系统的状态矩阵,Q{\rm Q}Q是给定的正定对称矩阵,P{\rm P}P是李雅普诺夫方程AP+PAT+Q=0{\rm AP+PA^T+Q=0}AP+PAT+Q=0的解,即正定实对称矩阵P{\rm P}P,用于离散系统求解;
【实战】:已知系统状态矩阵A=[01−1−1]A=\begin{bmatrix}0 & 1\\-1 & -1\end{bmatrix}A=[0−11−1],给定正定对称矩阵Q=[1001]Q=\begin{bmatrix}1 & 0\\0 & 1\end{bmatrix}Q=[1001],确定李雅普诺夫方程的解P{\rm P}P;
解:
% 实例Chapter9.3.5
clc;clear;A=[0,1;-1,-1]; % 状态矩阵
Q=[1,0;0,1]; % 给定的正定对称矩阵
P=lyap(A',Q)% 求解得到的矩阵P
% P =
% 1.5000 0.5000
% 0.5000 1.0000
3.6 综合实例及MATLAB/SIMULINK应用
实验要求:已知线性定常系统状态空间表达式如下:
{[x1′x2′x3′]=[0100−21−10−1][x1x2x3]+[001]uy=[100][x1x2x3]\begin{cases} &\begin{bmatrix} x_1'\\ x_2'\\ x_3' \end{bmatrix}=\begin{bmatrix} 0 & 1 & 0\\ 0 & -2 & 1\\ -1 & 0 & -1 \end{bmatrix}\begin{bmatrix} x_1\\ x_2\\ x_3 \end{bmatrix}+\begin{bmatrix} 0\\0\\1 \end{bmatrix}u\\\\ &y=\begin{bmatrix} 1 & 0 & 0 \end{bmatrix}\begin{bmatrix} x_1\\ x_2\\ x_3 \end{bmatrix} \end{cases} ⎩⎨⎧x1′x2′x3′=00−11−2001−1x1x2x3+001uy=[100]x1x2x3
使用MATLAB{\rm MATLAB}MATLAB进行以下分析:
- 分析系统的可控性、可观测性;
- 对系统进行非奇异线性变换,使其状态转移矩阵对角化,进而分析变换后系统的可控性、可观性;
- 分析系统的稳定性,绘制系统的阶跃响应曲线;
- 使用LTIViewer{\rm LTI\ Viewer}LTI Viewer工具绘制上述系统的阶跃响应和冲激响应曲线;
解:
【STEP1{\rm STEP1}STEP1】:建立控制系统的数学模型。
% 实例Chapter9.3.6
clc;clear;% 建立系统的数学模型
A=[0,1,0;0,-2,1;-1,0,-1];
B=[0;0;1];C=[1,0,0];D=0;
sys=ss(A,B,C,D)
% 控制系统数学模型结果
sys =A = x1 x2 x3x1 0 1 0x2 0 -2 1x3 -1 0 -1B = u1x1 0x2 0x3 1C = x1 x2 x3y1 1 0 0D = u1y1 0
【STEP2{\rm STEP2}STEP2】:系统的可控性、可观性。
% 控制系统的可控性、可观性
control_matrix=ctrb(A,B);
rank_control=rank(control_matrix);if rank_control<3disp('系统不可控!');
elsedisp('系统完全可控!');
endobserve_matrix=obsv(A,C);
rank_observe=rank(observe_matrix);if rank_observe<3disp('系统不可观!');
elsedisp('系统完全可观!');
end
% 系统的可控性、可观性结果
系统完全可控!
系统完全可观!
【STEP3{\rm STEP3}STEP3】:对系统进行线性对角化变换。
% 系统进行线性对角化变换
[V,S]=eig(A); % 求取矩阵特征值和特征向量
if rank(V)==3 % 矩阵满秩,进行对角化变换AA=inv(V)*A*V;BB=inv(V)*B;CC=C*V;disp('系统对角化变换后的新系统模型:');sys_diag=ss(AA,BB,CC,D)
elsedisp('这个系统不可对角化!');
end
% 线性对角化变换后系统模型
系统对角化变换后的新系统模型:sys_diag =A = x1 x2 x3x1 -0.338+0.562i -5e-16-2.5e-16i 2.78e-17+6.18e-16ix2 -3.89e-16+2.78e-16i -0.338-0.562i -8.33e-17-8.4e-16ix3 3.33e-16+1.95e-16i 3.33e-16-2.21e-16i -2.32-4.99e-17iB = u1x1 0.593+0.398ix2 0.593-0.398ix3 -0.619-1.57e-18iC = x1 x2 x3y1 -0.459-0.39i -0.459+0.39i -0.379D = u1y1 0
【STEP4{\rm STEP4}STEP4】:线性变换后系统可控性、可观性。
% 线性变换后控制系统的可控性、可观性
control_matrix=ctrb(AA,BB);
rank_control=rank(control_matrix);if rank_control<3disp('变换后系统不可控!');
elsedisp('变换后系统完全可控!');
endobserve_matrix=obsv(AA,CC);
rank_observe=rank(observe_matrix);if rank_observe<3disp('变换后系统不可观!');
elsedisp('变换后系统完全可观!');
end% 线性变换后可控性、可观性结果
% 变换后系统完全可控!
% 变换后系统完全可观!
【STEP5{\rm STEP5}STEP5】:分析系统的稳定性。
% 利用李雅普诺夫方法分析系统的稳定性
P=lyap(A',eye(3))% 系统稳定性结果:P矩阵为正定矩阵,系统渐近稳定。
%P =
% 3.5000 1.5000 0.5000
% 1.5000 1.0000 0.5000
% 0.5000 0.5000 1.0000【STEP6{\rm STEP6}STEP6】:绘制系统的阶跃响应曲线。
% 绘制系统的阶跃响应曲线
step(sys)
set(findobj(get(gca,'Children'),'LineWidth',0.5),'LineWidth',1.5);
title('控制系统阶跃响应','FontSize',15);
【STEP7{\rm STEP7}STEP7】:使用LTIViewer{\rm LTI\ Viewer}LTI Viewer工具进行分析。
ltiview;
【完整代码】
% 实例Chapter9.3.6
clc;clear;% STEP1:建立系统的数学模型
A=[0,1,0;0,-2,1;-1,0,-1];
B=[0;0;1];C=[1,0,0];D=0;
sys=ss(A,B,C,D)% STEP2:控制系统的可控性、可观性
control_matrix=ctrb(A,B);
rank_control=rank(control_matrix);if rank_control<3disp('系统不可控!');
elsedisp('系统完全可控!');
endobserve_matrix=obsv(A,C);
rank_observe=rank(observe_matrix);if rank_observe<3disp('系统不可观!');
elsedisp('系统完全可观!');
end% STEP3:系统进行线性对角化变换
[V,S]=eig(A); % 求取矩阵特征值和特征向量
if rank(V)==3 % 矩阵满秩,进行对角化变换AA=inv(V)*A*V;BB=inv(V)*B;CC=C*V;disp('系统对角化变换后的新系统模型:');sys_diag=ss(AA,BB,CC,D)
elsedisp('这个系统不可对角化!');
end% STEP4:线性变换后控制系统的可控性、可观性
control_matrix=ctrb(AA,BB);
rank_control=rank(control_matrix);if rank_control<3disp('变换后系统不可控!');
elsedisp('变换后系统完全可控!');
endobserve_matrix=obsv(AA,CC);
rank_observe=rank(observe_matrix);if rank_observe<3disp('变换后系统不可观!');
elsedisp('变换后系统完全可观!');
end% STEP5:利用李雅普诺夫方法分析系统的稳定性
P=lyap(A',eye(3))% STEP6:绘制系统的阶跃响应曲线
step(sys)
set(findobj(get(gca,'Children'),'LineWidth',0.5),'LineWidth',1.5);
title('控制系统阶跃响应','FontSize',15); 相关文章:

Chapter9.3:线性系统稳定性分析及综合实例
该系列博客主要讲述Matlab软件在自动控制方面的应用,如无自动控制理论基础,请先学习自动控制系列博文,该系列博客不再详细讲解自动控制理论知识。 自动控制理论基础相关链接:https://blog.csdn.net/qq_39032096/category_10287468…...
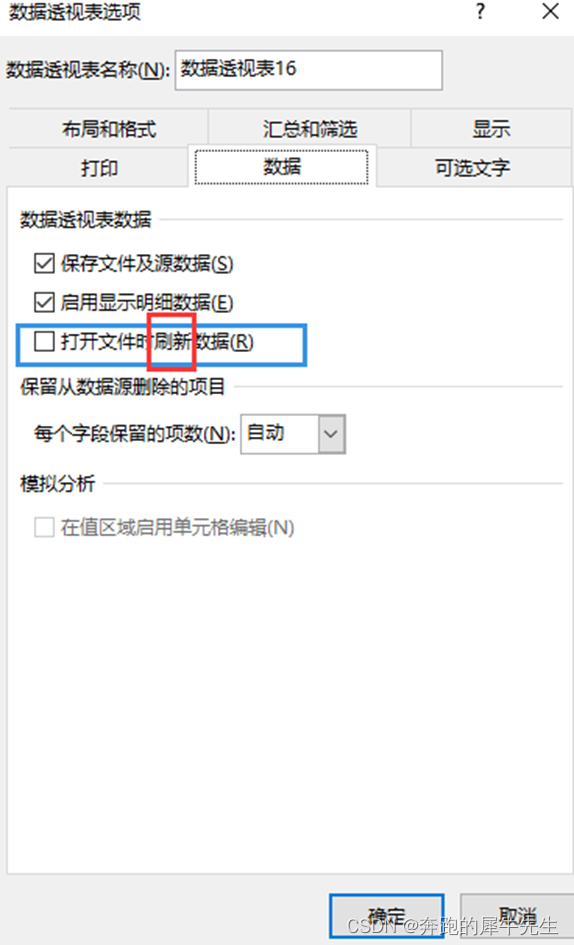
EXCEL 在复杂查询时摒弃vlookup() sumif() 等公式,而使用数据透视表的初步学习
1 为什么要用数据透视表 如果不用,就可能需要写很复杂的,查询公式 比如,vlookup各种sumif,sumifs 等等,如果还是多个表进行统计,那写起来更酸爽所以感觉 vlookup sumif,sumifs 更适合,简单情况下的查询&am…...

C 文件读写
C 文件读写 本章我们将介绍 C 程序员如何创建、打开、关闭文本文件或二进制文件。 一个文件,无论它是文本文件还是二进制文件,都是代表了一系列的字节。C 语言不仅提供了访问顶层的函数,也提供了底层(OS)调用来处理存…...

Linux中实现程序开机自启——将程序配置为系统服务
一、需求说明 当我们在Linux系统上安装软件时,希望软件实现开机自启,或程序崩溃后自动重启,提升软件运行的稳定性;而linux系统中的systemd刚好可以满足我们的要求(可将软件注册为系统服务)。 二、systemd systemd 是一个 Linux 系统基础组件的集合,提供了一个系统和服务…...
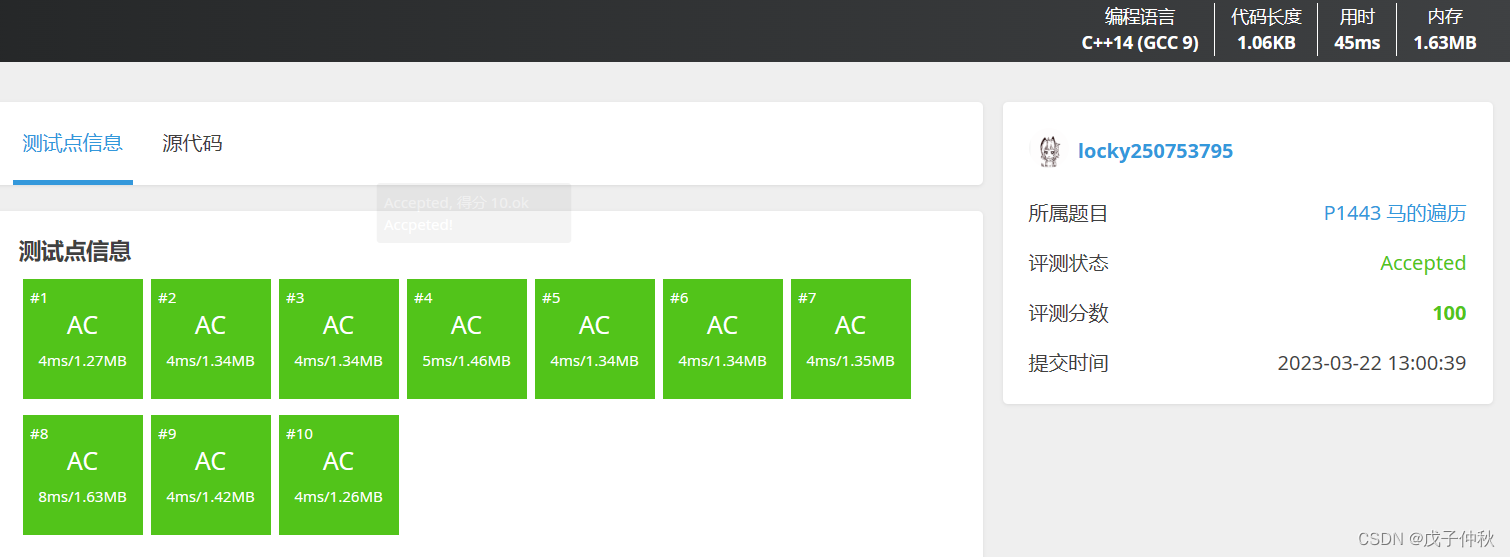
【洛谷刷题】蓝桥杯专题突破-广度优先搜索-bfs(13)
目录 写在前面: 题目:P1443 马的遍历 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn) 题目描述: 输入格式: 输出格式: 输入样例: 输出样例: 解题思路: 代码: AC &am…...

【新2023Q2模拟题JAVA】华为OD机试 - 总最快检测效率 or 核酸检测效率
最近更新的博客 华为od 2023 | 什么是华为od,od 薪资待遇,od机试题清单华为OD机试真题大全,用 Python 解华为机试题 | 机试宝典【华为OD机试】全流程解析+经验分享,题型分享,防作弊指南华为od机试,独家整理 已参加机试人员的实战技巧本篇题解:报数 题目 一百个人围成一圈…...

基于主成分分析的混音方法
一、简介: 基于主成分分析的混音方法是一种常见的音频混音技术,它利用主成分分析(PCA)对音频信号进行降维和重构,从而实现混音。 二、基本步骤如下: 采集和存储需要混音的音频信号。 对音频信号进行主成分…...
Code Two Exchange Crack
CodeTwo Exchange 迁移允许直接从早期版本的 Exchange(从 Exchange 2010 开始)安全、轻松地迁移到 Exchange 2019 和 2016。此服务器应用程序还允许您集中管理来自 Microsoft 365 (Office 365) 的邮箱迁移以及来自基于 IMAP 的电子邮件系统(例…...

jQuery.form.js 详细用法_维护老项目使用
概述 jquery-3.3.1.min.js : http://jquery.com/download jquery.form.min.js :http://malsup.com/jquery/form/#tab7 jquery form 是一个表单异步提交的插件,可以很容易提交表单,设置表单提交的参数,并在表单提交前…...

【Java】关于你不知道的Java大整数运算之BigInteger类超级好用!!!
目录 一、BigInteger类简单介绍 二、BigInteger构造方式 (1)构造方式 (2)输入方式 三、BigInteger常见的成员方法 (1)方法介绍 (2)方法使用演示 1.加减乘除余 2.比较 3.绝…...
运维是不是没有出路了?
瑞典马工的《是时候让运维集体下岗了》一出,就让运维人为之一颤,人人自危。文章开篇就提到:明人不说暗话,在云原生和DevOps成熟的今天,运维作为一个岗位和团队已经完成了历史任务,应该退出舞台了…...
【C++笔试强训】第七天
选择题 解析:内联函数(inline)一般用于代码较少,代码块里面没有递归且频繁调用的函数,是一种以空间换时间(不是指内存,而是指令变多编译出来的可执行程序会变大)的做法。内联函数在预…...

mysql binlog 一直追加写,磁盘满了怎么办?
文章目录 mysql binlog 清理策略1、设置binlog最大的文件数和文件大小2、定时清理过期binlog文件3、手动清理binlog文件4、禁用或启用binlogmysql binlog用于记录mysql数据库所有变更(数据库的DDL、DML操作)包括用户执行的语句,以及底层引擎所执行的操作的二进制日志,主要用…...
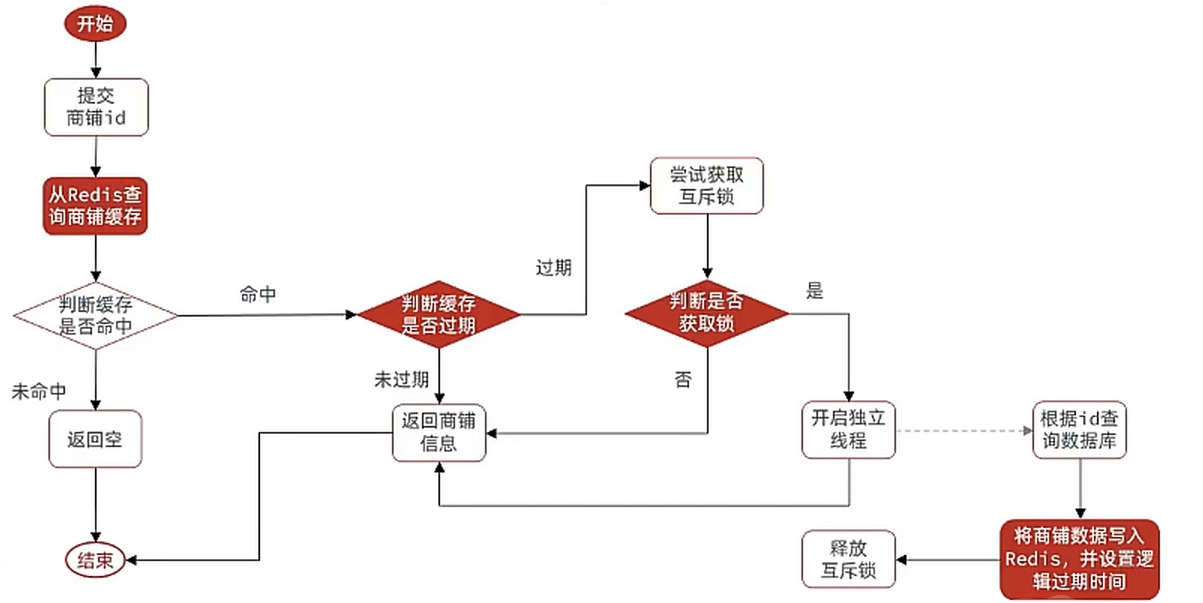
缓存穿透、缓存雪崩、缓存击穿解决方案
什么是缓存 缓存就是数据交换的缓冲区(称作Cache),是存贮数据的临时地方,一般读写性能较高。 添加 redis 缓存 给店铺类型查询业务添加缓存 需求:添加ShopTypeController中的queryTypeList方法,添加查询缓存 缓存更新…...
web + servlet + jdbc mysql 实现简单的表单管理界面
目录数据库创建数据库连接servlet创建,这里注意一下我的数据库我自己改了一下名字lhx网页html运行文件目录展示首先我们准备好开发使用的工具以及配置 idea2020 tomcat8.5 创建javaweb参考idea编译Tomcat详细步骤 IDEA通过JDBC连接数据库请参考jdbc连接数据库 需要登陆注册界面…...

Maven 国内镜像仓库
镜像仓库目标 当我们未定义任何远程仓库时,使用 Maven 更新依赖时,其会去默认远程仓库中拉取,默认远程仓库 是国外地址,所以在国内访问特别慢,想提升访问速度,需要将国外地址换成国内地址 更换仓库地址的…...

day21 ● 530.二叉搜索树的最小绝对差 ● 501.二叉搜索树中的众数 ● 236. 二叉树的最近公共祖先
二叉搜索树的最小绝对差 二叉搜索树(Binary Search Tree,简称 BST)是一种特殊的二叉树,它的每个节点都满足以下条件: 左子树上所有节点的值均小于该节点的值;右子树上所有节点的值均大于该节点的值&#…...
专业推荐竞赛 / 证书 官网及赛事相关信息整理)
大学计算机(软件类)专业推荐竞赛 / 证书 官网及赛事相关信息整理
大学计算机专业(软件)推荐竞赛 / 证书 官网及赛事相关信息 一、算法类(丰富简历): 1、ACM国际大学生程序设计竞赛: 官网:https://icpc.global/ 国内:http://icpc.pku.edu.cn/index.htm 报名方式:区域预赛一般每年9-1…...

Metasploit入门到高级【第九章】
预计更新第一章:Metasploit 简介 Metasploit 是什么Metasploit 的历史和发展Metasploit 的组成部分 第二章:Kali Linux 入门 Kali Linux 简介Kali Linux 安装和配置常用命令和工具介绍 第三章:Metasploit 基础 Metasploit 的基本概念Met…...

JDK之8后: 协程? 虚拟线程!!!
特性官方文档: https://openjdk.org/jeps/436 Java协程 近三十年来,Java 开发人员一直依赖线程作为并发服务器应用程序的构建块。每个方法中的每个语句都在线程内执行,并且由于 Java 是多线程的,因此多个执行线程同时发生。线程是Java的并发…...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...

Docker 本地安装 mysql 数据库
Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ;并安装。 基础操作不再赘述。 打开 macOS 终端,开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...

【Redis】笔记|第8节|大厂高并发缓存架构实战与优化
缓存架构 代码结构 代码详情 功能点: 多级缓存,先查本地缓存,再查Redis,最后才查数据库热点数据重建逻辑使用分布式锁,二次查询更新缓存采用读写锁提升性能采用Redis的发布订阅机制通知所有实例更新本地缓存适用读多…...
Axure零基础跟我学:展开与收回
亲爱的小伙伴,如有帮助请订阅专栏!跟着老师每课一练,系统学习Axure交互设计课程! Axure产品经理精品视频课https://edu.csdn.net/course/detail/40420 课程主题:Axure菜单展开与收回 课程视频:...
