【算法题解】22. 接雨水
这是一道 困难 题
题目来自: https://leetcode.cn/problems/trapping-rain-water/
题目
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。
示例 1:

输入:height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出:6
解释:上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图,在这种情况下,可以接 6 个单位的雨水(蓝色部分表示雨水)。
示例 2:
输入:height = [4,2,0,3,2,5]
输出:9
提示:
- n==height.lengthn == height.lengthn==height.length
- 1<=n<=2∗1041 <= n <= 2 * 10^41<=n<=2∗104
- 0<=height[i]<=1050 <= height[i] <= 10^50<=height[i]<=105
解题思路
使用单调栈的思路,假如给定的每个柱子是逐个变矮的,那么可以接的雨水就是0。
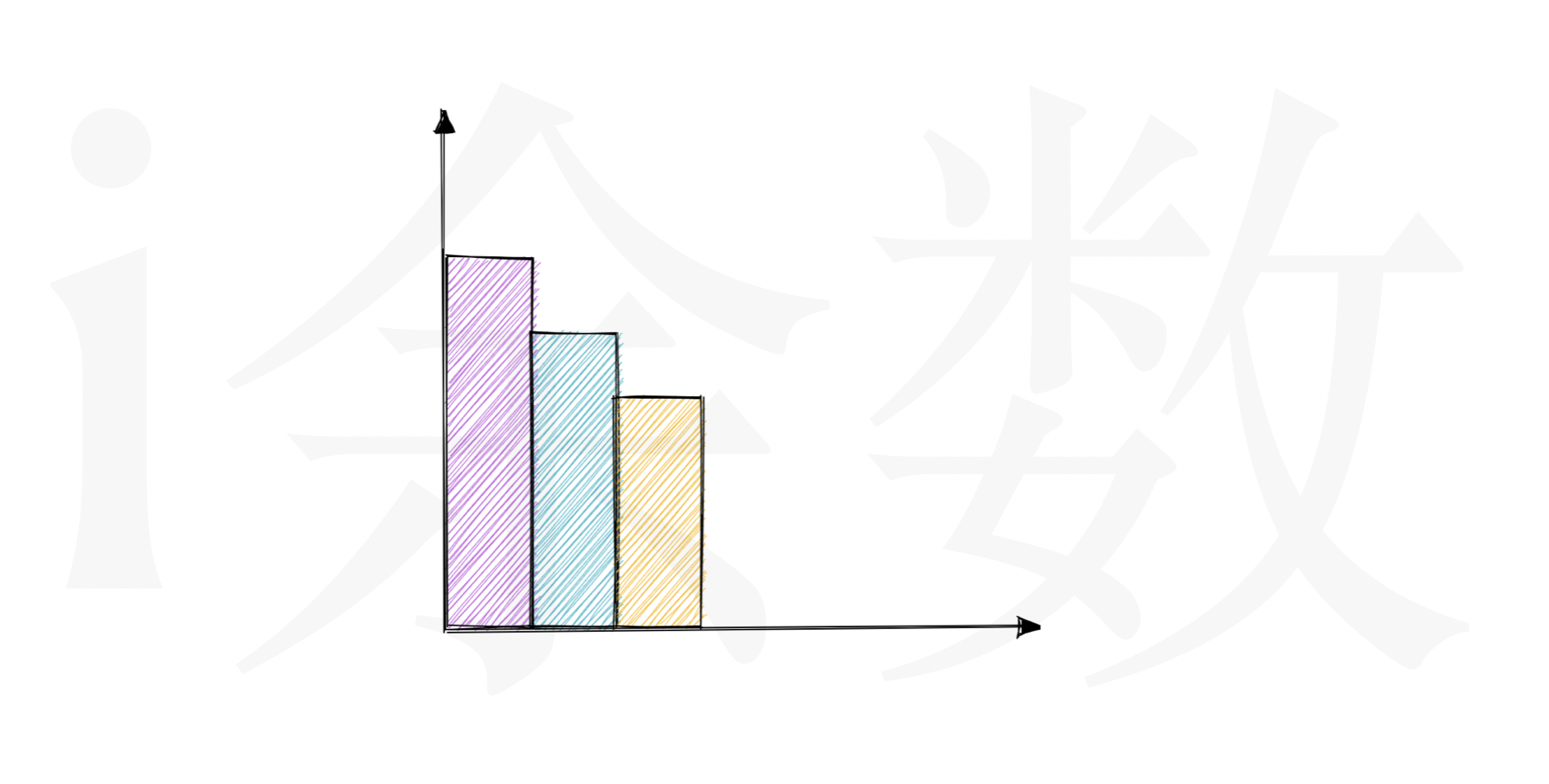
如果这时候突然来了一个变高的柱子 4 ,那么这个柱子就会使得当前柱状图可以接雨水了。

如上图所示:
- 先将栈顶的柱子取出(柱子3),使用(其左边柱子的高度和新增柱子高度的最小值 - 其本身高度)* 其宽度,得出当前柱子的接水量,累加到答案中。(注意:如果栈中目前只有一个柱子的话,其左边高度设为
0,即不可以接水。) - 这时如果新的栈顶柱子(柱子2)依然比新增的柱子矮,继续取出栈顶柱子并计算其接水量,注意这是宽度应该是柱子3的宽度 + 柱子2的宽度。
- 这时栈顶柱子1的高度 大于 新增的柱子4 的高度,柱子4入栈,注意:这时柱子4的宽度 = 柱子2 + 柱子3 + 柱子4 的总宽度,即前面所有出栈的柱子的宽度都需要保留下来,因为如果再来一个第5个柱子的高度 > 柱子4的高度的话,前面那么宽度还是有用的。
代码实现
Java 代码实现
class Solution {private Deque<int[]> stack = new LinkedList<>();public int trap(int[] height) {int n = height.length ;if(n <= 1){return 0;}int ans = 0;for(int h : height){int w = 0;while(!stack.isEmpty() && h > stack.peek()[1]){int[] top = stack.pop();w += top[0];if(!stack.isEmpty()){ans += w * (Math.min(stack.peek()[1], h) - top[1]);}}stack.push(new int[]{w + 1, h});}return ans;}
}
Go 代码实现
func trap(height []int) int {n := len(height)if n <= 1 {return 0}stack := [][]int{}ans := 0for _, h := range height {if len(stack) == 0 {stack = append(stack, []int{1, h})continue}w := 0for len(stack) > 0 && h > stack[len(stack) - 1][1] {top := stack[len(stack) - 1]stack = stack[:len(stack) - 1]w += top[0]if len(stack) > 0 {ans += w * (min(stack[len(stack) - 1][1], h) - top[1])}}stack = append(stack, []int{w + 1, h})}return ans
}func min(a int, b int) int {if a > b {return b}return a
}
复杂度分析
时间复杂度:O(n)O(n)O(n)
空间复杂度:O(n)O(n)O(n)
相关文章:

【算法题解】22. 接雨水
这是一道 困难 题 题目来自: https://leetcode.cn/problems/trapping-rain-water/ 题目 给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。 示例 1: 输入:height [0,…...
集合的遍历)
集合详解之(四)集合的遍历
文章目录🐒个人主页🏅JavaSE系列专栏📖前言:🎀ArrayList集合forEach()方法遍历🎀for循环遍历(针对List集合)🪅增强for循环(也支持Set集合)&#x…...
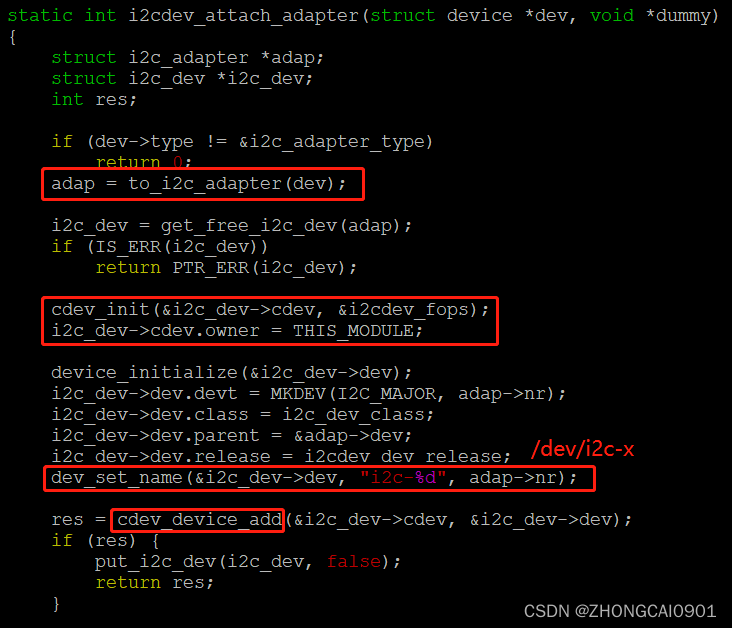
【I2C】通用驱动i2c-dev分析
文章目录1. 前言2. i2c-dev驱动的注册过程3. open_i2c_dev函数分析4. set_slave_addr函数分析5. i2c_read_bytes函数分析1. 前言 前面分析i2c-tool测试工具就是基于drivers/i2c/i2c-dev.c驱动来实现的。i2c-dev驱动在加载时会遍历所有的I2C总线(i2c_bus_type)上所有注册的adap…...

用GPT-4写代码不用翻墙了?Cursor告诉你:可以~~
目录 一、介绍 二、使用方法 三、其他实例 1.正则表达式 2.自动化测试脚本 3.聊聊技术 一、介绍 Cursor主要功能是根据用户的描述写代码或者进行对话,对话的范围仅限技术方面。优点是不用翻墙、不需要账号。Cursor基于GPT模型,具体什么版本不祥&#…...

硬件语言Verilog HDL牛客刷题day03 时序逻辑部分
1.VL21 根据状态转移表实现时序电路 1.题目: 某同步时序电路转换表如下,请使用D触发器和必要的逻辑门实现此同步时序电路,用Verilog语言描述。 2.解题思路 2.1 首先同步时序电路 , 时钟上升沿触发, 复位信号rst 低电…...

day31 ● 455.分发饼干 ● 376. 摆动序列 ● 53. 最大子序和
● 455.分发饼干 ● 376. 摆动序列 ● 53. 最大子序和 在本次的题目中,我们使用了贪心算法来解决三个问题:分发饼干、摆动序列、最大子序和。这三个问题都可以使用贪心算法来解决,而且贪心算法的时间复杂度相对较低,能够在较短的…...
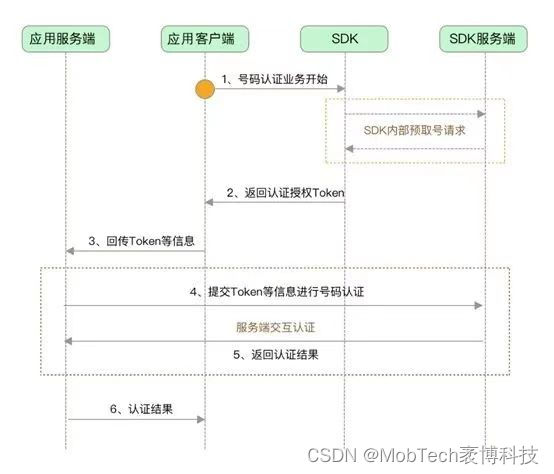
MobTech 秒验|本机号码一键登录会泄露隐私吗
本机号码一键登录是一种新型的应用登录方式,它可以利用运营商的数据网关认证能力,实现手机号免密登录,提高用户体验和转化率,降低验证成本和流失率。本机号码一键登录支持三大运营商号码认证,3秒内完成手机号验证&…...
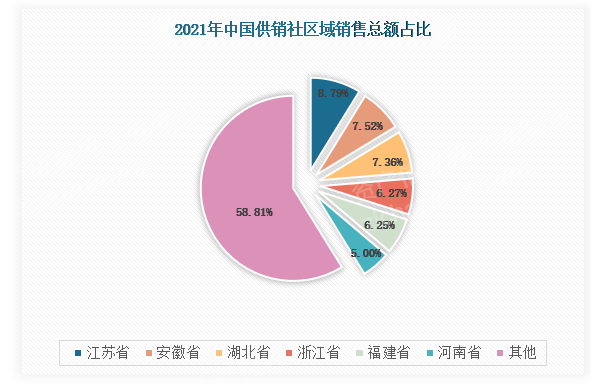
2023年供销合作社研究报告
第一章 行业概况 1.1 供销合作社概述 中华全国供销合作总社,是中华人民共和国全国供销合作社的联合组织。中华全国供销合作总社的前身可以追溯到1949年11月成立的中央合作事业管理局。在新中国成立初期,供销合作社就基本形成了自上而下、覆盖全国的组织…...
【ansible】实施任务控制
目录 实施任务控制 一,循环(迭代)--- loop 1,利用loop----item循环迭代任务 2,item---loop循环案例 1,定义item循环列表 2,通过变量应用列表格式 3,字典列表(迭代嵌套子…...

49天精通Java,第11天,java接口和抽象类的异同,default关键字
目录一、什么是接口二、接口的特点三、接口和类的区别四、接口和抽象类的区别五、接口的声明方式六、default默认方法大家好,我是哪吒。 一、什么是接口 Java接口是一系列方法的声明,是一些方法特征的集合,一个接口只有方法的特征没有方法的…...

JAVA练习99-逆波兰表达式求值
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 目录 前言 一、题目-逆波兰表达式求值 1.题目描述 2.思路与代码 2.1 思路 2.2 代码 总结 前言 提示:这里可以添加本文要记录的大概内容: 4月5…...
恶意软件、恶意软件反杀技术以及反病毒技术的详细介绍
1.恶意软件简单介绍恶意软件是指在计算机系统上执行恶意任务的病毒、蠕虫和特洛伊木马的程序,通过破坏软件进程来实施控制。腾讯移动安全实验室发布的数据显示,恶意软件由多种威胁组成,会不断弹出,所以需要采取多种方法和技术来进…...

【数据库运维】mysql备份恢复练习
目录 数据库备份,数据库为school,素材如下 1.创建student和score表 2.为student表和score表增加记录 3.备份数据库school到/backup目录 4.备份MySQL数据库为带删除表的格式,能够让该备份覆盖已有数据库而不需要手动删除原有数据库 5.直接将My…...

刷题30-对称的二叉树
对称的二叉树 思路:用递归,首先明白递归中止的条件是什么 搬用别人的看法: 做递归思考三步: 1.递归的函数要干什么? 函数的作用是判断传入的两个树是否镜像。 输入:TreeNode left, TreeNode right 输出…...

精选简历模板
1.应届生通用简历模板(.docx) 适用于应届生找工作的学生群体 https://download.csdn.net/download/weixin_43042683/87652099https://download.csdn.net/download/weixin_43042683/87652099 部分缩略图如下: 2.研究生通用简历模板(.docx)…...
蓝桥杯嵌入式第十三届客观题解析
文章目录 前言一、题目1二、题目2三、题目3四、题目4五、题目5六、题目6七、题目7八、题目8九、题目9十、题目10总结前言 本篇文章将带大家来学习蓝桥杯嵌入式的客观题了,蓝桥杯嵌入式的客观题涉及到模电,数电,单片机等知识,需要非常扎实的基础,客观题不能急于求成只能脚…...
【Redis】线程问题
文章目录单线程版本演化工作流程为什么逐渐又加入了多线程特性?影响Redis性能的主要因素->网络I/O多线程工作流程Unix网络编程中的五种I/O模型I/O多路复用工作原理:select、poll、epoll为什么Redis快单线程与多线程的比较配置文件开启多线程单线程 版本演化 Re…...

【算法题】2498. 青蛙过河 II
题目: 给你一个下标从 0 开始的整数数组 stones ,数组中的元素 严格递增 ,表示一条河中石头的位置。 一只青蛙一开始在第一块石头上,它想到达最后一块石头,然后回到第一块石头。同时每块石头 至多 到达 一次。 一次…...

【新2023Q2押题JAVA】华为OD机试 - 整理扑克牌
最近更新的博客 华为od 2023 | 什么是华为od,od 薪资待遇,od机试题清单华为OD机试真题大全,用 Python 解华为机试题 | 机试宝典【华为OD机试】全流程解析+经验分享,题型分享,防作弊指南华为od机试,独家整理 已参加机试人员的实战技巧本篇题解:整理扑克牌 题目 给定一组数…...
【hello C语言】文件操作
目录 1. 什么是文件? 2. 程序文件 3. 数据文件 4. 文件名 5. 文件类型 5.1 二进制文件 5.2 文本文件 5.3 数据在内存中的存储 6. 文件缓冲区 7. 文件指针 8. 文件的打开和关闭 9. 文件的顺序读写 10. 文件的随机读写 10.1 fseek:根据文件指针的位置和偏移…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

vue3 字体颜色设置的多种方式
在Vue 3中设置字体颜色可以通过多种方式实现,这取决于你是想在组件内部直接设置,还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法: 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...

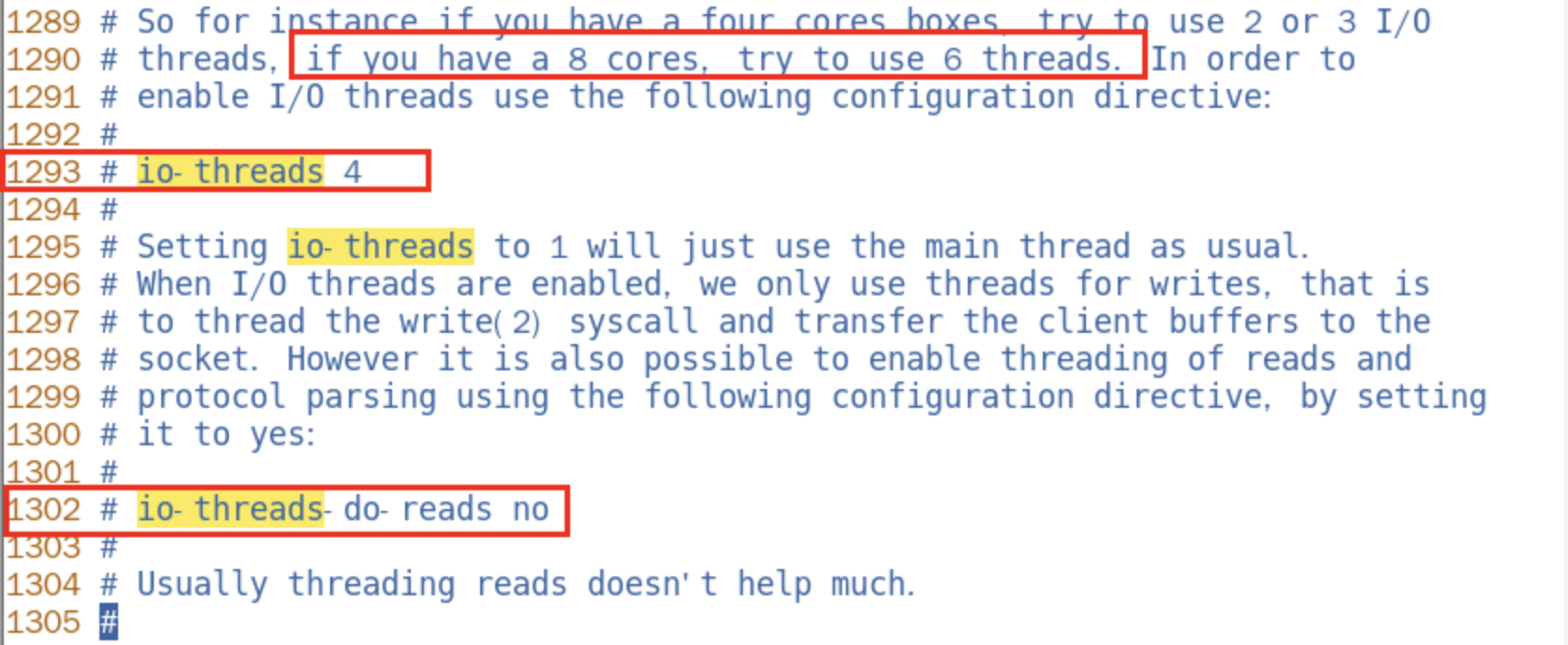
华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...
