【图论】(二)图论基础与路径问题
图论基础与路径问题
- 图的构造
- 邻接矩阵
- 邻接表
- 所有可达路径
- 邻接矩阵存储
- 邻接表存储
- 字符串接龙
- 有向图的完全可达性
图的构造
这里仅对图论路径问题中图的构造做整理总结归纳,具体详细相关概念请参考代码随想录上的整理总结:
- 图论理论基础
- 深度优先搜索理论基础
- 所有可达路径-dfs实战
- 广度优先搜索理论基础
我们如何用代码来表示一个图呢?
一般使用邻接表、邻接矩阵或者用类来表示。
邻接矩阵
- 邻接矩阵使用二维数组来表示图结构。 邻接矩阵是从节点的角度来表示图,有多少节点就申请多大的二维数组。
- 例如:
grid[2][5] = 6,表示 节点 2 连接 节点5 为有向图,节点2 指向 节点5,边的权值为6。 - 如果想表示无向图,即:
grid[2][5] = 6,grid[5][2] = 6,表示节点2 与 节点5 相互连通,权值为6

-
在一个 n (节点数)为8 的图中,就需要申请 8 * 8 这么大的空间。
-
这种表达方式(邻接矩阵) 在 边少,节点多的情况下,会导致申请过大的二维数组,造成空间浪费。
-
而且在寻找节点连接情况的时候,需要遍历整个矩阵,即 n * n 的时间复杂度,同样造成时间浪费。
邻接矩阵的优点:
- 表达方式简单,易于理解
- 检查任意两个顶点间是否存在边的操作非常快
- 适合稠密图,在边数接近顶点数平方的图中,邻接矩阵是一种空间效率较高的表示方法。
缺点:
- 遇到稀疏图,会导致申请过大的二维数组造成空间浪费
- 遍历 边 的时候需要遍历整个n * n矩阵,造成时间浪费
邻接表
邻接表 使用 数组 + 链表的方式来表示。 邻接表是从边的数量来表示图,有多少边 才会申请对应大小的链表。
邻接表的构造如图:

这里表达的图是:
- 节点1 指向 节点3 和 节点5
- 节点2 指向 节点4、节点3、节点5
- 节点3 指向 节点4
- 节点4指向节点1
有多少边 邻接表才会申请多少个对应的链表节点。
从图中可以直观看出 使用 数组 + 链表 来表达 边的连接情况
邻接表的优点:
- 对于稀疏图的存储,只需要存储边,空间利用率高
- 遍历节点连接情况相对容易
缺点:
- 检查任意两个节点间是否存在边,效率相对低,需要 O(V)时间,V表示某节点连接其他节点的数量。
- 实现相对复杂,不易理解
所有可达路径
卡码网题目链接(ACM模式)
力扣题目链接 - 797. 所有可能的路径
题目描述:
给定一个有 n 个节点的有向无环图,节点编号从 1 到 n。请编写一个函数,找出并返回所有从节点 1 到节点 n 的路径。每条路径应以节点编号的列表形式表示。
输入描述:
- 第一行包含两个整数 N,M,表示图中拥有 N 个节点,M 条边
- 后续 M 行,每行包含两个整数 s 和 t,表示图中的 s 节点与 t 节点中有一条路径
输出描述: 输出所有的可达路径,路径中所有节点的后面跟一个空格,每条路径独占一行,存在多条路径,路径输出的顺序可任意。如果不存在任何一条路径,则输出 -1。
注意输出的序列中,最后一个节点后面没有空格! 例如正确的答案是 1 3 5,而不是 1 3 5 , 5后面没有空格!
输入示例:
5 5
1 3
3 5
1 2
2 4
4 5
输出示例:
1 3 5
1 2 4 5
提示信息:

写在前面:
- 在上述谈到图的两张存储方式中,这里通过两种方式逐一巩固。
- 此外,本题是目是深度优先搜索比较好的入门题,若对深搜不清楚的需先提前了解深度搜索理论与过程。
邻接矩阵存储
- 邻接矩阵 使用 二维数组来表示图结构, 邻接矩阵是从节点的角度来表示图,有多少节点就申请多大的二维数组。
- 本题有n 个节点,因为节点标号是从1开始的,为了节点标号和下标对齐,我们申请
n + 1 * n + 1这么大的二维数组。vector<vector<int>> graph(n + 1, vector<int>(n + 1, 0)); - 输入每行两个整数 s 和 t,表示图中的 s 节点与 t 节点中有一条路径,则表示
graph[s][t] = 1;,输入m条边程序则有:while (m--) {cin >> s >> t;// 使用邻接矩阵 ,1 表示 节点s 指向 节点tgraph[s][t] = 1; }
深搜三部曲:
1. 确认递归函数,参数
- 首先我们dfs函数一定要存一个图,用来遍历,需要存一个目前我们遍历的节点,定义为x
- 还需要存一个n,表示终点,我们遍历的时候,用来判断当 x==n 时候 标明找到了终点
- 至于 单一路径 和 路径集合 可以放在全局变量,那么代码是这样的:
vector<vector<int>> result; // 收集符合条件的路径 vector<int> path; // 0节点到终点的路径 // x:目前遍历的节点 // graph:存当前的图 // n:终点 void dfs (const vector<vector<int>>& graph, int x, int n) {
2. 确认终止条件
当目前遍历的节点 为 最后一个节点 n 的时候 就找到了一条 从出发点到终止点的路径。
// 当前遍历的节点x 到达节点n
// 找到符合条件的一条路径
if (x == n)
{ result.push_back(path);return;
}
3. 处理目前搜索节点出发的路径
接下来是走 当前遍历节点x的下一个节点。
首先是要找到 x节点指向了哪些节点呢? 遍历方式是这样的:
for (int i = 1; i <= n; i++) // 遍历节点x链接的所有节点
{ if (graph[x][i] == 1) // 找到 x指向的节点,就是节点i{ }
}
接下来就是将 选中的x所指向的节点,加入到 单一路径来
path.push_back(i); // 遍历到的节点加入到路径中来
进入下一层递归
dfs(graph, i, n); // 进入下一层递归
最后就是回溯的过程,撤销本次添加节点的操作
path.pop_back(); // 回溯,撤销本节点
该过程整体代码:
for (int i = 1; i <= n; i++) // 遍历节点x链接的所有节点
{ if (graph[x][i] == 1) // 找到 x链接的节点{path.push_back(i); // 遍历到的节点加入到路径中来dfs(graph, i, n); // 进入下一层递归path.pop_back(); // 回溯,撤销本节点}
}
程序实现:
#include <iostream>
#include <vector>
#include <algorithm>
#include <queue>using namespace std;vector<vector<int>> result; // 手机符合条件的路径
vector<int> path; //0节点到终点的路径
// graph:存当前的图
// x:目前遍历的节点
// n:终点
void dfs(const vector<vector<int>> graph, int x, int n)
{// 当前遍历的节点x 到达节点n if(x == n){result.push_back(path);return;}// 遍历节点x链接的所有节点for(int i = 1; i <= n; i++){// 找到 x指向的节点,就是节点iif(graph[x][i] == 1){// 将选中的x所指向的节点,加入到 单一路径来。path.push_back(i);// 进入下一层递归dfs(graph,i,n);// 回溯的过程,撤销本次添加节点的操作path.pop_back();}}
}int main()
{// m条边 n个节点 // graph[s][t] = 1表示节点s可以指向tint m,n,s,t;cin >> n >> m;vector<vector<int>> graph(n+1, vector<int>(n+1,0));while(m--){cin >> s >> t;// 使用邻接矩阵 表示无线图,1 表示 s 与 t 是相连的graph[s][t] = 1;}// 任何路径都是从节点1开始path.push_back(1);// 开始遍历dfs(graph,1,n);// 打印结果if(result.size() == 0)cout << -1 << endl;for(int i = 0; i < result.size(); i++){for(int j = 0; j < result[i].size() - 1; j++){cout << result[i][j] << " ";}cout << result[i][result[i].size() - 1] << endl;}return 0;
}
邻接表存储
用邻接表存储和邻接矩阵存储的区别只需要修改图的定义存储、dfs函数内的参数以及对链表的遍历,核心框架、思路均不变。
程序实现:
//邻接表法
vector<vector<int>> result; // 手机符合条件的路径
vector<int> path; //0节点到终点的路径
// graph:存当前的图
// x:目前遍历的节点
// n:终点
void dfs(const vector<list<int>> graph, int x, int n)
{// 当前遍历的节点x 到达节点n if(x == n){result.push_back(path);return;}// 遍历节点x链接的所有节点for(int node: graph[x]){// 将选中的x所指向的节点,加入到 单一路径来。path.push_back(node);// 进入下一层递归dfs(graph,node,n);// 回溯的过程,撤销本次添加节点的操作path.pop_back();}
}int main()
{// m条边 n个节点 // graph[s][t] = 1表示节点s可以指向tint m,n,s,t;cin >> n >> m;vector<list<int>> graph(n+1);while(m--){cin >> s >> t;// 使用邻接矩阵 表示无线图,1 表示 s 与 t 是相连的graph[s].push_back(t);}// 任何路径都是从节点1开始path.push_back(1);// 开始遍历dfs(graph,1,n);// 打印结果if(result.size() == 0)cout << -1 << endl;for(int i = 0; i < result.size();i++){for(int j = 0; j < result[i].size() - 1; j++){cout << result[i][j] << " ";}cout << result[i][result[i].size() - 1] << endl;}return 0;
}
字符串接龙
卡码网题目链接(ACM模式)
题目描述:
字典 strList 中从字符串 beginStr 和 endStr 的转换序列是一个按下述规格形成的序列:
- 序列中第一个字符串是
beginStr。 - 序列中最后一个字符串是
endStr。 - 每次转换只能改变一个字符。
- 转换过程中的中间字符串必须是字典 strList 中的字符串。
给你两个字符串 beginStr 和 endStr 和一个字典 strList,找到从 beginStr 到 endStr 的最短转换序列中的字符串数目。如果不存在这样的转换序列,返回 0。
输入描述:
第一行包含一个整数 N,表示字典 strList 中的字符串数量。 第二行包含两个字符串,用空格隔开,分别代表 beginStr 和 endStr。 后续 N 行,每行一个字符串,代表 strList 中的字符串。
输出描述:
输出一个整数,代表从 beginStr 转换到 endStr 需要的最短转换序列中的字符串数量。如果不存在这样的转换序列,则输出 0。
输入示例:
6
abc def
efc
dbc
ebc
dec
dfc
yhn
输出示例:
4
提示信息: 从 startStr 到 endStr,在 strList 中最短的路径为 abc -> dbc -> dec -> def,所以输出结果为 4

本题只需要求出最短路径的长度就可以了,不用找出具体路径。
所以这道题要解决两个问题:
- 图中的线是如何连在一起的
- 起点和终点的最短路径长度
首先题目中并没有给出点与点之间的连线,而是要我们自己去连,条件是字符只能差一个。
所以判断点与点之间的关系,需要判断是不是差一个字符,如果差一个字符,那就是有链接。
然后就是求起点和终点的最短路径长度,这里无向图求最短路,广搜最为合适,广搜只要搜到了终点,那么一定是最短的路径。 因为广搜就是以起点中心向四周扩散的搜索。
本题如果用深搜,会比较麻烦,要在到达终点的不同路径中选则一条最短路。 而广搜只要达到终点,一定是最短路。
另外需要有一个注意点:
- 本题是一个无向图,需要用标记位,标记着节点是否走过,否则就会死循环!
- 使用set来检查字符串是否出现在字符串集合里更快一些
程序实现:
#include <iostream>
#include <string>
#include <queue>
#include <unordered_set>
#include <unordered_map>using namespace std;int main()
{int n;string beginStr;string endStr;string str;unordered_set<string> strSet; // 字典 存放每一个字符串cin >> n;cin >> beginStr >> endStr;for(int i = 0; i < n;i++){cin >> str;strSet.insert(str);}// 记录strSet里的字符串是否被访问过,同时记录路径长度unordered_map<string, int> visitMap; // <记录的字符串,路径长度>// 初始化队列queue<string> que;que.push(beginStr);// 加入队列即标记访问visitMap.insert(pair<string,int>(beginStr, 1));while(!que.empty()){// 获取队头字符串,拿出来string word = que.front();que.pop();// 这个字符串在路径中的长度为 visitMap[word]int path = visitMap[word];// 开始在这个str中,挨个字符去替换for(int i = 0; i < word.size(); i++){// 用一个新字符串替换str,因为每次要置换一个字符string newWord = word;// 遍历26的字母for(int j = 0; j < 26; j++){newWord[i] = j + 'a';// 发现替换字母后,字符串与终点字符串相同if(newWord == endStr){cout << path + 1 << endl; // 找到了路径 return 0;}// 字符串集合里出现了newWord,并且newWord没有被访问过if (strSet.find(newWord) != strSet.end() && visitMap.find(newWord) == visitMap.end()){// 添加访问信息,并将新字符串放到队列中visitMap.insert(pair<string, int>(newWord, path + 1));que.push(newWord);}}}}// 没找到输出0return 0;
}
有向图的完全可达性
卡码网题目链接(ACM模式)
题目描述:
给定一个有向图,包含 N 个节点,节点编号分别为 1,2,…,N。现从 1 号节点开始,如果可以从 1 号节点的边可以到达任何节点,则输出 1,否则输出 -1。
输入描述:
第一行包含两个正整数,表示节点数量 N 和边的数量 K。 后续 K 行,每行两个正整数 s 和 t,表示从 s 节点有一条边单向连接到 t 节点。
输出描述: 如果可以从 1 号节点的边可以到达任何节点,则输出 1,否则输出 -1。
输入示例:
4 4
1 2
2 1
1 3
2 4
输出示例:
1
提示信息:

思路
本题给我们是一个有向图, 因此路径是存在方向的
递归三部曲:
1. 确认递归函数,参数
需要传入地图,当前的节点数(到当前节点是通路),同时还需要一个数组,用来记录我们都走过了哪些节点,这样好知道最后有没有把所有房间都遍历的。
所以 递归函数参数如下:
// key 当前的节点数(到当前节点是通路)
// visited 记录访问过的房间
void dfs(const vector<list<int>>& graph, int key, vector<bool>& visited) {
2. 确认终止条件
遍历的时候,什么时候终止呢?这里有一个很重要的逻辑,就是在递归中,是处理当前访问的节点,还是处理下一个要访问的节点
如果我们是处理当前访问的节点,当前访问的节点如果是 true ,说明是访问过的节点,那就终止本层递归,如果不是true,我们就把它赋值为true,因为这是我们处理本层递归的节点。
代码就是这样的:
// 写法一:处理当前访问的节点
void dfs(const vector<list<int>>& graph, int key, vector<bool>& visited) {if (visited[key]) {return;}visited[key] = true;list<int> keys = graph[key]; // 获取当前节点连接的节点链表for (int key : keys) {// 深度优先搜索遍历dfs(graph, key, visited);}
}
如果我们是处理下一层访问的节点,而不是当前层。那么就要在 深搜三部曲中第三步:处理目前搜索节点出发的路径的时候对 节点进行处理。
这样的话,就不需要终止条件,而是在 搜索下一个节点的时候,直接判断 下一个节点是否是我们要搜的节点。
代码就是这样的:
// 写法二:处理下一个要访问的节点
void dfs(const vector<list<int>>& graph, int key, vector<bool>& visited) {list<int> keys = graph[key]; // 获取当前节点连接的节点链表for (int key : keys){// 确认下一个是没访问过的节点if(visited[key] == false) {visited[key] = true;dfs(graph, key, visited);}}
}
可以看出,如何看待 我们要访问的节点,直接决定了两种不一样的写法
上述程序中,好像没有发现回溯的逻辑。本题是需要判断 1节点 是否能到所有节点,那么我们就没有必要回溯去撤销操作了,只要遍历过的节点一律都标记上。
那什么时候需要回溯操作呢?
当我们需要搜索一条可行路径的时候,就需要回溯操作了,因为没有回溯,就没法“调头”,
程序实现:
#include <iostream>
#include <vector>
#include <list>using namespace std;// key 当前得到的可以
// visited 记录访问过的房间
void dfs(vector<list<int>>& graph, int key, vector<bool>& visited)
{list<int> keys = graph[key]; // 获取当前节点下挂的节点链表for(int key: keys){if(visited[key] == false) // 遍历每一个节点 并做dfs标记{visited[key] = true;dfs(graph,key,visited);}}
}int main()
{int n, m, s, t;cin >> n >> m;vector<list<int>> graph(n+1);while(m--){cin >> s >> t;graph[s].push_back(t);}vector<bool> visited(n + 1, false);visited[1] = true; // 节点1 预先处理dfs(graph, 1, visited); // dfs计算能到达的最远节点,能到达并做标记for(int i = 1; i <= n; i++){if(visited[i] == false){cout << -1 << endl; return 0;}}cout << 1 << endl; return 0;
}
相关文章:

【图论】(二)图论基础与路径问题
图论基础与路径问题 图的构造邻接矩阵邻接表 所有可达路径邻接矩阵存储邻接表存储 字符串接龙有向图的完全可达性 图的构造 这里仅对图论路径问题中图的构造做整理总结归纳,具体详细相关概念请参考代码随想录上的整理总结: 图论理论基础深度优先搜索理…...
)
Git常用命令(持续更新中)
mkdir one 在当前目录下创建一个名为one的文件夹 cd one 进入one 文件夹 git init 初始化git 仓库 touch README.md 创建一个后缀为.md的新文件README.md git add README.md 将README.md添加到git暂存区 git add * . * 将所有文件添加到暂存区 git add "E:/t…...
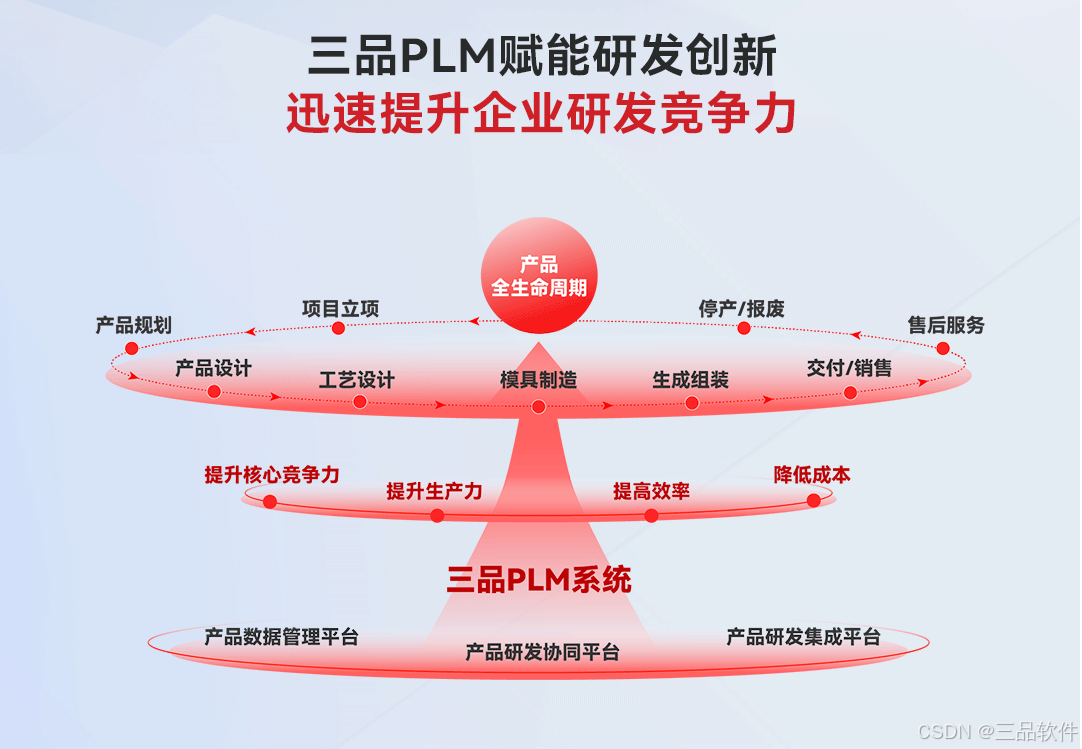
什么是PLM系统?PLM系统对制造业起到哪些作用?三品PLM系统对汽车制造业意义
在当今竞争激烈的制造业环境中,企业面临着来自市场、技术、客户需求等多方面的挑战。为了应对这些挑战,许多制造企业纷纷引入产品生命周期管理PLM系统,以实现更高效、更灵活的产品全生命周期管理。PLM系统以其独特的优势,在优化产…...

Pr 视频效果:元数据和时间码刻录
视频效果/视频/元数据和时间码刻录 Video/Metadata & Timecode Burn-in 元数据和时间码刻录 Metadata & Timecode Burn-in效果是一种在视频画面上叠加显示剪辑元数据或时间码的工具。它允许在导出视频时,将需用的元数据信息直接刻录在画面上,方便…...

前端MD5加密
1.导入包 npm install --save ts-md5 2.使用方式 import { Md5 } from ts-md5;//md5加密后的密码 const md5PwdMd5.hashStr("123456").toUpperCase(); 3. Vue解析token中携带的数据 3.1 安装插件 npm install jwt-decode --save 3.2 引入 import {jwtDecode} fro…...

仿IOS桌面悬浮球(支持拖拽、自动吸附、自动改变透明度与点击、兼容PC端与移动端)
使用 pointerdown/pointermove/pointerup 实现仿IOS桌面悬浮球效果,支持拖拽、指定拖拽选对容器,指定拖拽安全区、自动吸附、自动改变透明度与点击,兼容PC端与移动端。 效果展示 https://code.juejin.cn/pen/7423757568268304421 代码实现 …...
智谱开放平台API调用解析
一、什么是智谱AI 智谱AI成立于2019年,由清华大学计算机系知识工程实验室的技术成果转化而来,是一家致力于人工智能技术研发和应用的公司。智谱致力于打造新一代认知智能大模型,专注于做大模型的中国创新。 二、智谱开放平台API调用 官方文…...

Linux中定时删除10天前的日志文件
例如:删除/data/log/目录下所有10天前的.log文件 find /data/log/ -type f -name "*.log" -mtime 10 -exec rm -f {} \;只查看要删除的文件有哪些,不真正删除文件 logfiles$(find /data/log/ -type f -name "*.log" -mtime 10) ec…...

贝壳Android面试题及参考答案
详细说Final关键字 在编程语言中,final关键字具有重要的作用。以下为你详细介绍final关键字: 一、final关键字的主要作用 修饰变量 当final修饰基本数据类型变量时,该变量的值一旦被初始化就不能再被改变。例如:final int num = 10;num = 20; // 这会导致编译错误当final修…...
基于vue的酒店预订管理系统(源码+定制+开发)
博主介绍: ✌我是阿龙,一名专注于Java技术领域的程序员,全网拥有10W粉丝。作为CSDN特邀作者、博客专家、新星计划导师,我在计算机毕业设计开发方面积累了丰富的经验。同时,我也是掘金、华为云、阿里云、InfoQ等平台…...

FreeRTOS——TCB任务控制块、任务句柄、任务栈详解
任务控制块结构体 任务控制块是 FreeRTOS 中用于描述和管理任务的数据结构,包含了任务的状态、优先级、堆栈等信息。 TCB_t的全称为Task Control Block,也就是任务控制块,这个结构体包含了一个任务所有的信息,它的定义以及相关变…...

【STM32单片机_(HAL库)】4-5-2【定时器TIM】【感应开关盖垃圾桶项目】HC-SR04超声波模块实验
1.硬件 STM32单片机最小系统HC-SR04超声波模块 2.软件 hcsr04驱动文件添加main.c程序 #include "sys.h" #include "delay.h" #include "led.h" #include "uart1.h" #include "hcsr04.h"int main(void) {HAL_Init(); …...

安全网络架构
网络安全解决方案是指通过一系列技术和措施来保护网络系统和数据的安全。它涉及多个方面,包括网络设备的防护、数据的加密和备份、安全策略的制定和执行等。以下是一些常见的网络安全解决方案: 防火墙:防火墙是一种硬件或软件设备,…...

【万字长文】Word2Vec计算详解(二)Skip-gram模型
【万字长文】Word2Vec计算详解(二)Skip-gram模型 写在前面 本篇介绍Word2Vec中的第二个模型Skip-gram模型 【万字长文】Word2Vec计算详解(一)CBOW模型 markdown行 9000 【万字长文】Word2Vec计算详解(二)S…...

随机掉落的项目足迹:解决TypeError: Cannot read properties of undefined (reading ‘push‘)报错
问题引入 下面是request.js中请求拦截器相关的代码 但是运行时却出现了报错 问题解决 useRouter() 是 Vue Router 提供的组合式 API,它只能在 Vue 组件的 setup() 函数中有效。如果在其他地方(例如 Axios 的拦截器中)调用它,可…...

ChatTTS 本地安装和测试
Ubuntu 22服务器,3.9/3.10都可以,但是 3.11不可以 sudo apt install python3.10 apt install python3.10 python3.10-dev #ubuntu 22 安装python3.10对应的pip3.10 # 下载 get-pip.py curl -sS https://bootstrap.pypa.io/get-pip.py -o get-pip.py # 使…...

[Leetcode] 560 Subarray Sum Equals K
题意:给定一个数组求连续的子数组的和为k的有几个 Input: nums [1,1,1], k 2 Output: 2 https://leetcode.com/problems/subarray-sum-equals-k/description/ 首先思考1.因为是subarray sum前缀和很容易想到,那问题就转化成preSum[i] preSum[j] - k…...

TCL Android面试题大全及参考答案
能谈谈Jetpack组件吗? Jetpack 是一套用于 Android 开发的工具和组件库,它可以帮助开发者更高效地构建高质量的 Android 应用。 一、主要组件分类 架构组件: ViewModel:负责存储和管理与界面相关的数据,当屏幕旋转或配置发生变化时,ViewModel 可以帮助保存数据,避免数据…...

JVM错误:OutOfMemoryError: GC overhead limit exceeded
OutOfMemoryError: GC overhead limit exceeded 在Window服务器上跑一个项目,无意中出现服务访问不了,查看日志文档,第一次遇到了这个异常信息。 1. 错误含义 OutOfMemoryError: GC overhead limit exceeded 是 JVM 中的一种错误ÿ…...

Unity网络开发 - C#开源网络通信库PESocket的使用
概述 在现代多人在线游戏中,稳定且高效的网络通信是确保游戏体验的关键。本文将探讨如何利用C#开源网络通信库PESocket来构建一个简单的Unity客户端与.NET控制台服务器之间的实时消息传递系统。通过本例,读者不仅能够了解PESocket的基本用法,…...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...
Reasoning over Uncertain Text by Generative Large Language Models
https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829 1. 概述 文本中的不确定性在许多语境中传达,从日常对话到特定领域的文档(例如医学文档)(Heritage 2013;Landmark、Gulbrandsen 和 Svenevei…...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...

【Linux】Linux 系统默认的目录及作用说明
博主介绍:✌全网粉丝23W,CSDN博客专家、Java领域优质创作者,掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域✌ 技术范围:SpringBoot、SpringCloud、Vue、SSM、HTML、Nodejs、Python、MySQL、PostgreSQL、大数据、物…...
 + 力扣解决)
LRU 缓存机制详解与实现(Java版) + 力扣解决
📌 LRU 缓存机制详解与实现(Java版) 一、📖 问题背景 在日常开发中,我们经常会使用 缓存(Cache) 来提升性能。但由于内存有限,缓存不可能无限增长,于是需要策略决定&am…...

从面试角度回答Android中ContentProvider启动原理
Android中ContentProvider原理的面试角度解析,分为已启动和未启动两种场景: 一、ContentProvider已启动的情况 1. 核心流程 触发条件:当其他组件(如Activity、Service)通过ContentR…...

Elastic 获得 AWS 教育 ISV 合作伙伴资质,进一步增强教育解决方案产品组合
作者:来自 Elastic Udayasimha Theepireddy (Uday), Brian Bergholm, Marianna Jonsdottir 通过搜索 AI 和云创新推动教育领域的数字化转型。 我们非常高兴地宣布,Elastic 已获得 AWS 教育 ISV 合作伙伴资质。这一重要认证表明,Elastic 作为 …...

智能职业发展系统:AI驱动的职业规划平台技术解析
智能职业发展系统:AI驱动的职业规划平台技术解析 引言:数字时代的职业革命 在当今瞬息万变的就业市场中,传统的职业规划方法已无法满足个人和企业的需求。据统计,全球每年有超过2亿人面临职业转型困境,而企业也因此遭…...
