当前位置：首页 > news >正文

阿哈罗诺夫——玻姆效应（AB效应）

news 2025/11/10 4:32:14

规范变换

$\nabla \times (\nabla \times A)=\nabla(\nabla\cdot A)-\nabla^2A$

规范场是与物理规律的定域规范变换不变性相联系的物质场

$\oint A\,dl=\iint\nabla \times A\,dS$

$\nabla \times E=-\frac{\partial B}{\partial t}=-\frac{\partial (\nabla \times A)}{\partial t}=-\nabla\times \frac{\partial A}{\partial t}\Rightarrow \nabla\times(E+\frac{\partial A}{\partial t})=0$

纵场的旋度为零,横场的散度为零

$E+\frac{\partial A}{\partial t}=-\nabla \phi$

由于 $\nabla\times(\nabla g)=0$

因此 $B=\nabla\times A=\nabla\times(A+\nabla g)$

为了消除此影响，我们需要对标势场做规范
- 库伦规范(Coulomb gauge):使麦克斯韦方程组自然满足静电场的条件

$\nabla \cdot A=0$

- 洛伦兹规范（Lorentz gauge）:满足洛伦兹变换不变性

$\nabla \cdot A=-\frac{1}{c^2}\frac{\partial \phi}{\partial t}$

带电粒子在磁场中的总动量

电磁场的动量

$\vec{G_{e,m}}=\int_V\varepsilon _0(\vec{E}\times \vec{B})d\tau'= \int_V\varepsilon _0(\vec{E}\times (\nabla\times A))d\tau'$

稳定条件下， $\nabla\times E=0,\nabla\cdot A=0$

得到 $\vec{E}\times(\nabla\times A)=\nabla(\vec{A}\cdot \vec{E})-\nabla\cdot (\vec{A}\vec{E}+\vec{E}\vec{A})+\vec{A}(\nabla\cdot \vec{E})$

$\vec{G_{e,m}}=\varepsilon _{0}\left [ \int_V \vec{A}(\nabla \cdot\vec{E})d\tau' +\oint_S(\vec{A}\cdot\vec{E})dS' -\oint_S(\vec{A}\vec{E}+\vec{E}\vec{A})\cdot dS' \right ]=q\vec{A}$

因此，带电的运动粒子在外磁场中的总动量

$\vec{p}=m\vec{v}+q\vec{A}$

AB效应

量子力学中，电势与磁标势具有可观测的物理量的效应

AB实验装置

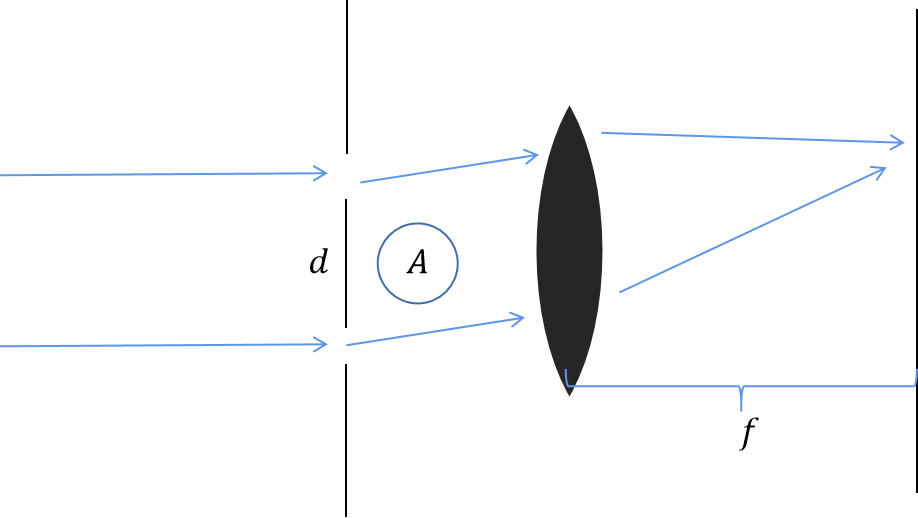
螺线管不通电时，电子波函数的相位是

$\phi = \int \vec{p}\cdot d\vec{r}$

通过两狭缝的电子波函数相位差

$\phi_1-\phi_2=kdsin\theta$

屏上暗纹的位置是

$y=f\,tan\theta\approx \frac{(2n+1)\pi}{k}\frac{f}{d}$

与电子速度共轭的正则动量为

$\vec{p}=m\vec{v}-e\vec{A}$

接通螺线管后

$\phi_1-\phi_2=kdsin\,\theta+\int_{c_1}-\frac{e\vec{A}}{\hbar}\cdot d \vec{r}-\int_{c_2}-\frac{e\vec{A}}{\hbar}\cdot d \vec{r}=kdsin\,\theta-\frac{e}{\hbar}\Phi$

因此，屏上干涉条纹位置为

$y'=ftan\,\theta\approx \left [ (2n+1)\pi+\frac{e}{\hbar}\Phi \right ]\frac{f}{kd}$

阿哈罗诺夫——玻姆效应（AB效应）

规范变换

带电粒子在磁场中的总动量

$\vec{p}=m\vec{v}+q\vec{A}$

AB效应

AB实验装置

相关文章：

阿哈罗诺夫——玻姆效应（AB效应）

sed使用

redhat9忘记root密码操作(普通用户也适用)

Android 五种启动模式小结

算法竞赛ICPC、CCPC、NIO、蓝桥杯、天梯赛

图像分割技术及经典实例分割网络Mask R-CNN（含基于Keras Python源码定义）

元宇宙和医疗保健

iOS_从相机或相册里扫描二维码或条形码

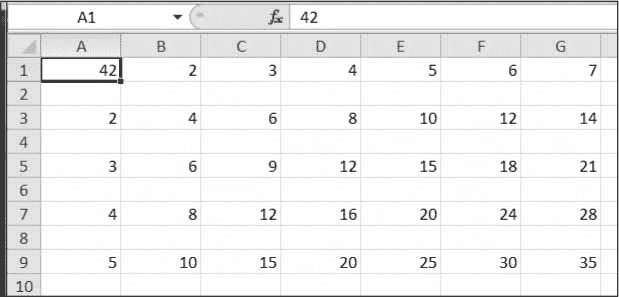
Python 自动化指南（繁琐工作自动化）第二版：十六、使用 CSV 文件和 JSON 数据

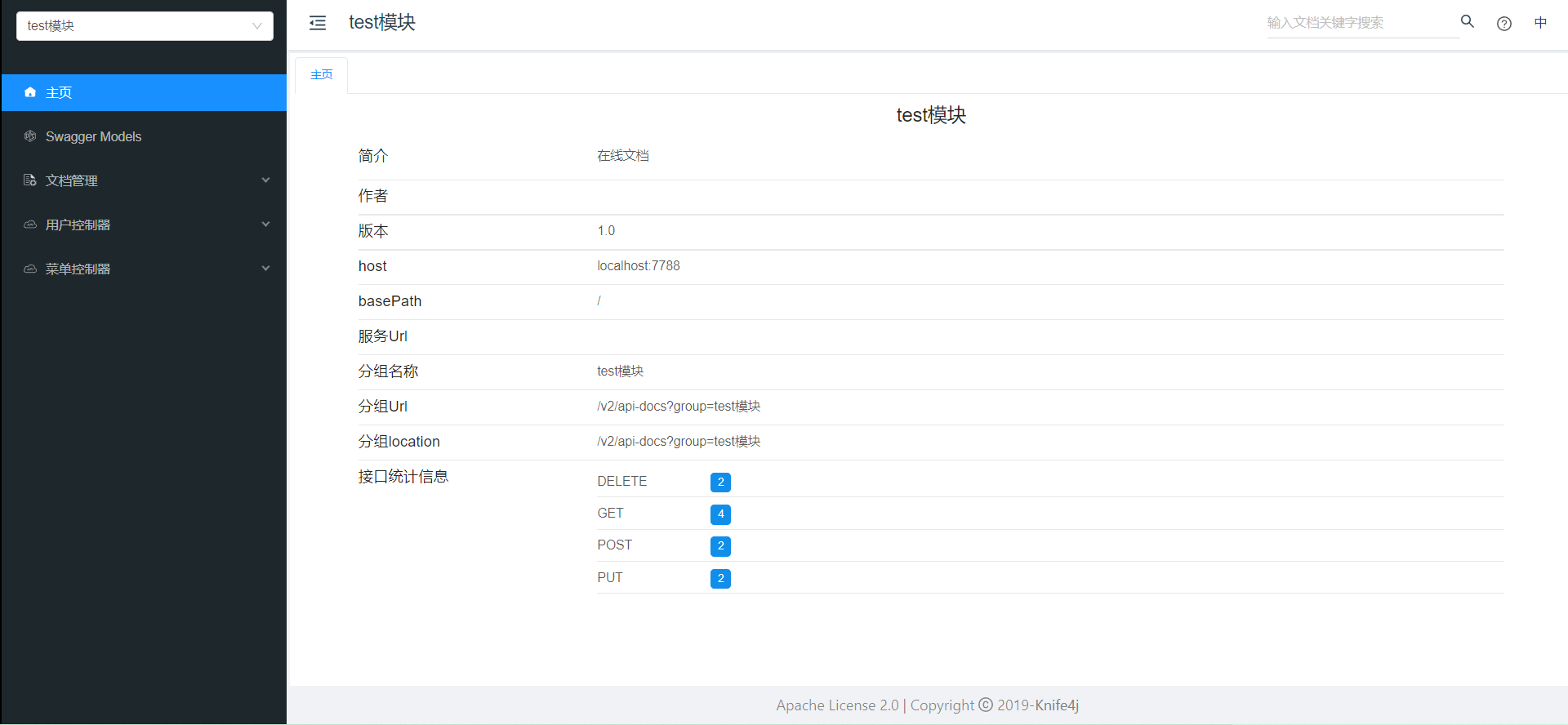
knife4j接口文档

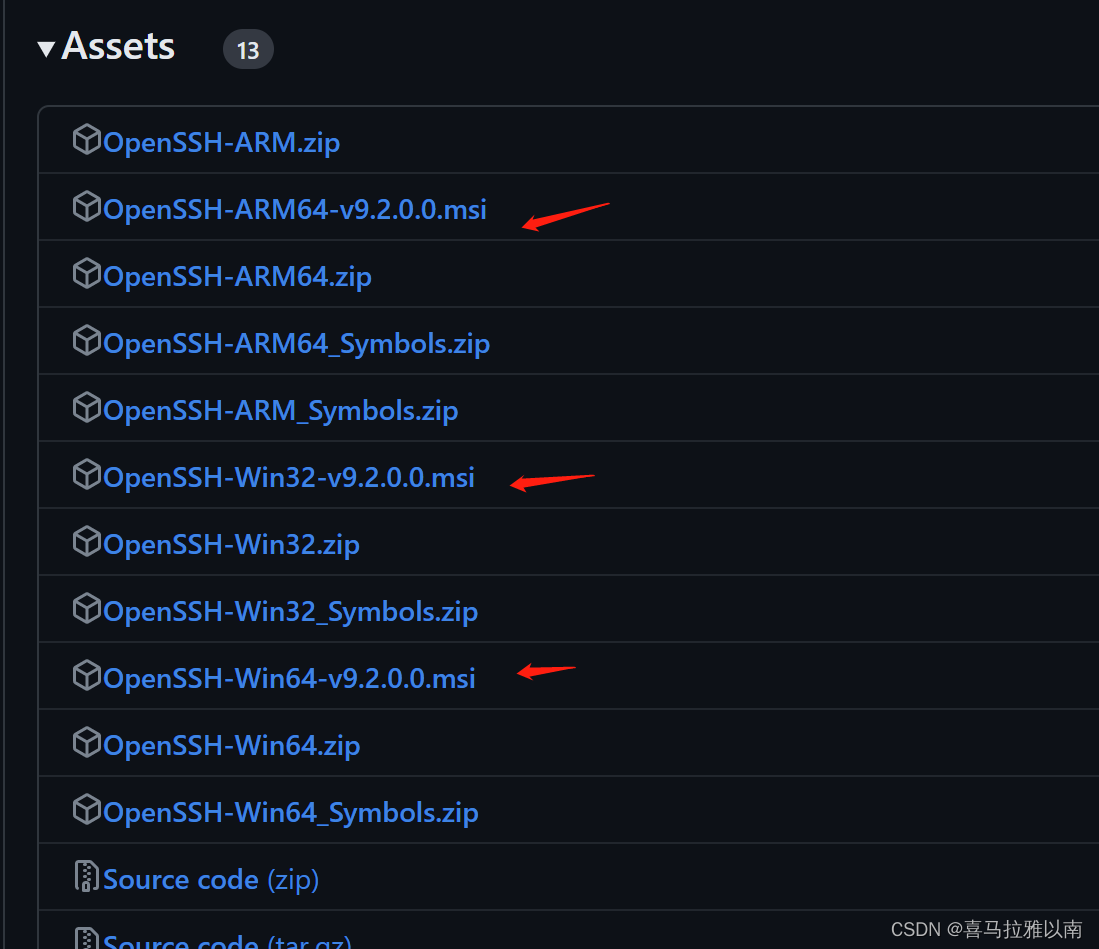
Windows机器安装SSH搭建，自己搞个局域网机房玩一玩

二叉树的前序遍历（力扣144）

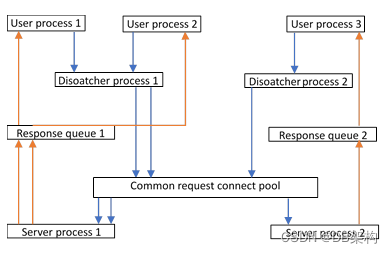
【数据库管理】①实例与数据库

vba：单元格的选择，查找，合并，批注，SpecialCells，图形插入

【内网安全】横向移动域控提权NetLogonADCSPACKDC永恒之蓝

将本地项目上传到远程仓库的步骤

selenium+opencv实现模拟登陆（滑块验证码）

辽宁申请互联网医院牌照流程

java实现布隆过滤器

gitlab部署及整合Jenkins持续构建（三）nexus私服的安装及实战、linux安装mysql

挑战杯推荐项目

【网络】每天掌握一个Linux命令 - iftop

【杂谈】-递归进化：人工智能的自我改进与监管挑战

docker详细操作--未完待续

模型参数、模型存储精度、参数与显存

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中，手势开发全攻略：

Swift 协议扩展精进之路：解决 CoreData 托管实体子类的类型不匹配问题（下）

vscode（仍待补充）

五年级数学知识边界总结思考-下册

JVM暂停（Stop-The-World，STW）的原因分类及对应排查方案