Windows机器安装SSH搭建,自己搞个局域网机房玩一玩
Windows机器安装SSH搭建
- 为啥要装SSH
- 安装OpenSSH
- 使用 Windows 设置来安装 OpenSSH
- ps脚本在线安装
- ps脚本离线安装
- 其他二进制安装包安装
为啥要装SSH
家里有多台Win机器,一台主机两个笔记本,本着不浪费的原则,打算把它们在平时的工作学习中利用起来。
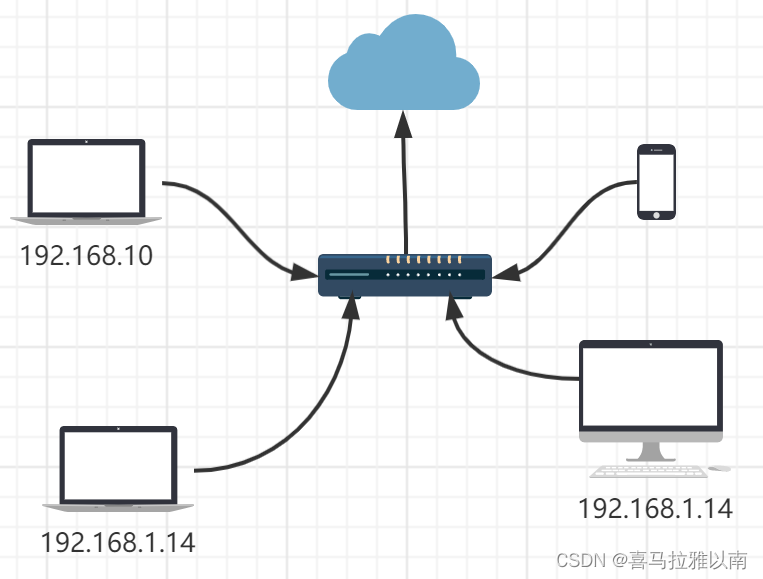
家里的三台电脑都链接了同一个路由器,所有设备都在同一个子网下面,那么只需要开启端口确定协议,那么所有设备均可以进行互通互联,包括Android手机也可以使用ADB工具进行控制,那就可以抱着笔记本Surface(一台非常轻的电脑)躺床上远程开发。
让我们梳理下目标:
- 使用笔记本连上台式机上远程开发
- 开发时提供集成环境(组件这些东西当然交给台式机啦)
- 控制Android手机进行一些自动化操作(需要将手机通过USB链接电脑并打开调试模式)
既然咱们目标确定了,那么来这些目标怎么实现呢,笔者以前操作linux比较多,那肯定毫无疑问,SSH协议通信必须是我最佳选择,再通过使用zsh、powershell、bash就能控制家里的所有设备了,嘻嘻,果然懒就是生产力。
安装OpenSSH
如果你有曾经有安装过git的话,那么指不定你的电脑可能已经存在ssh客户端了,客户端只能是让你的机器有了链接别人的能力。
下图就是ssh-client已安装并且已经配置到环境变量中。
使用CMD,或者powershell均可以执行ssh username@hostname,结合快捷键win+R食用更佳方便。
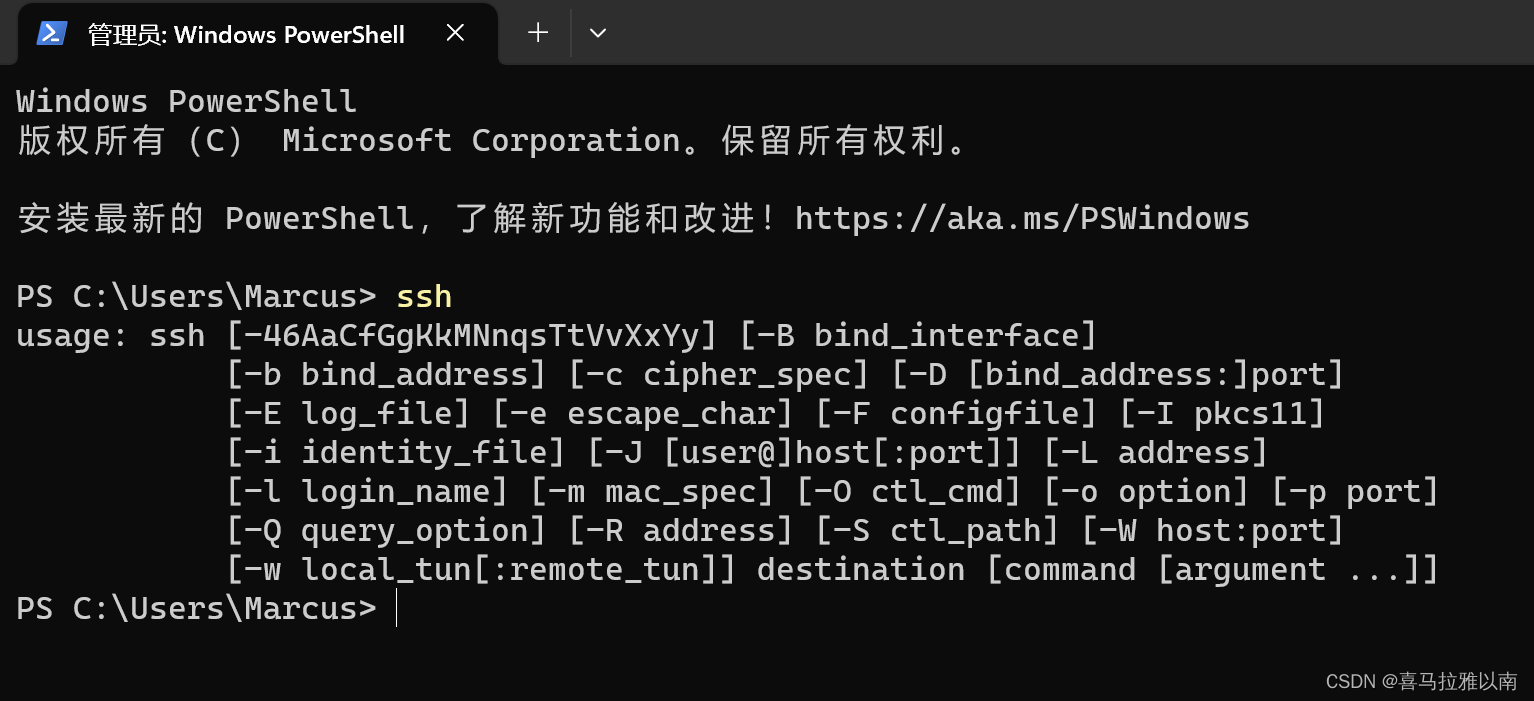
举个例子,你要约喜欢的女孩子去看电影,那么你得先要有时间+获取到电影票的能力,而你喜欢的女孩子没有时间,那就算你发起“请求”(邀约),也肯定不能约到的。

上图就是192.168.1.9这台机器不支持SSH协议链接,导致请求被拒(;´д`)ゞ
因此我们为了能链接上目标机器,需要给目标机器安装好能够接收到我们请求的服务端,即OpenSSH-Server。
接下来笔者会介绍三种安装OpenSSH的方法,更推荐脚本离线安装,又快又稳。
曾经笔者为了管理上百台windos服务器就是用的这个方法安装的,那服务器绝了,windowsXP、windows98 都有,这是没想到的。
使用 Windows 设置来安装 OpenSSH
可以使用 Windows Server 2019 和 Windows 10 设备上的 Windows 设置安装这两个 OpenSSH 组件。
- 打开“设置”,选择“应用” >“应用和功能”
- 然后选择“可选功能”,扫描列表,查看是否已安装 OpenSSH。
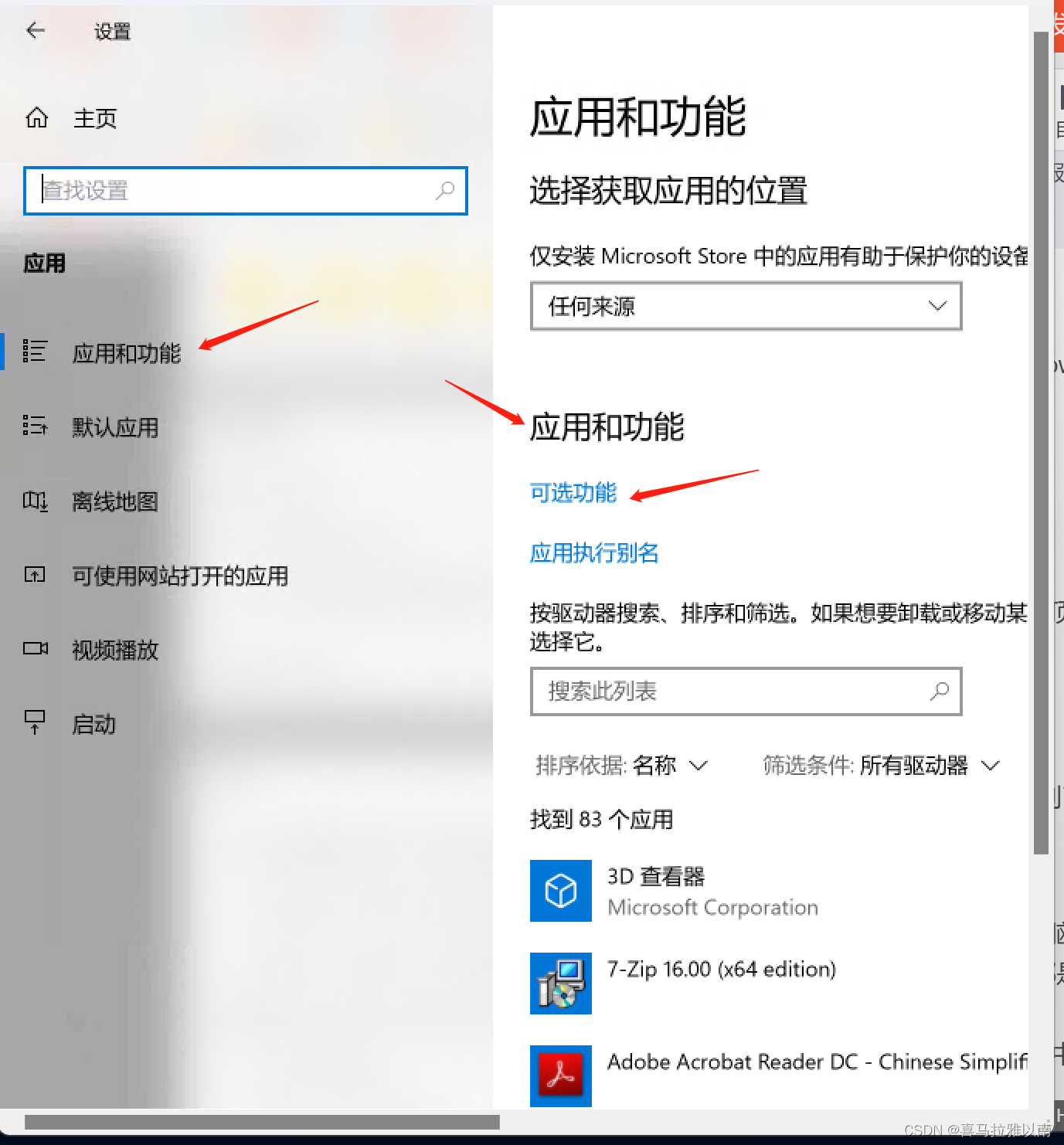
如果未安装,请在页面顶部选择“添加功能”,然后:
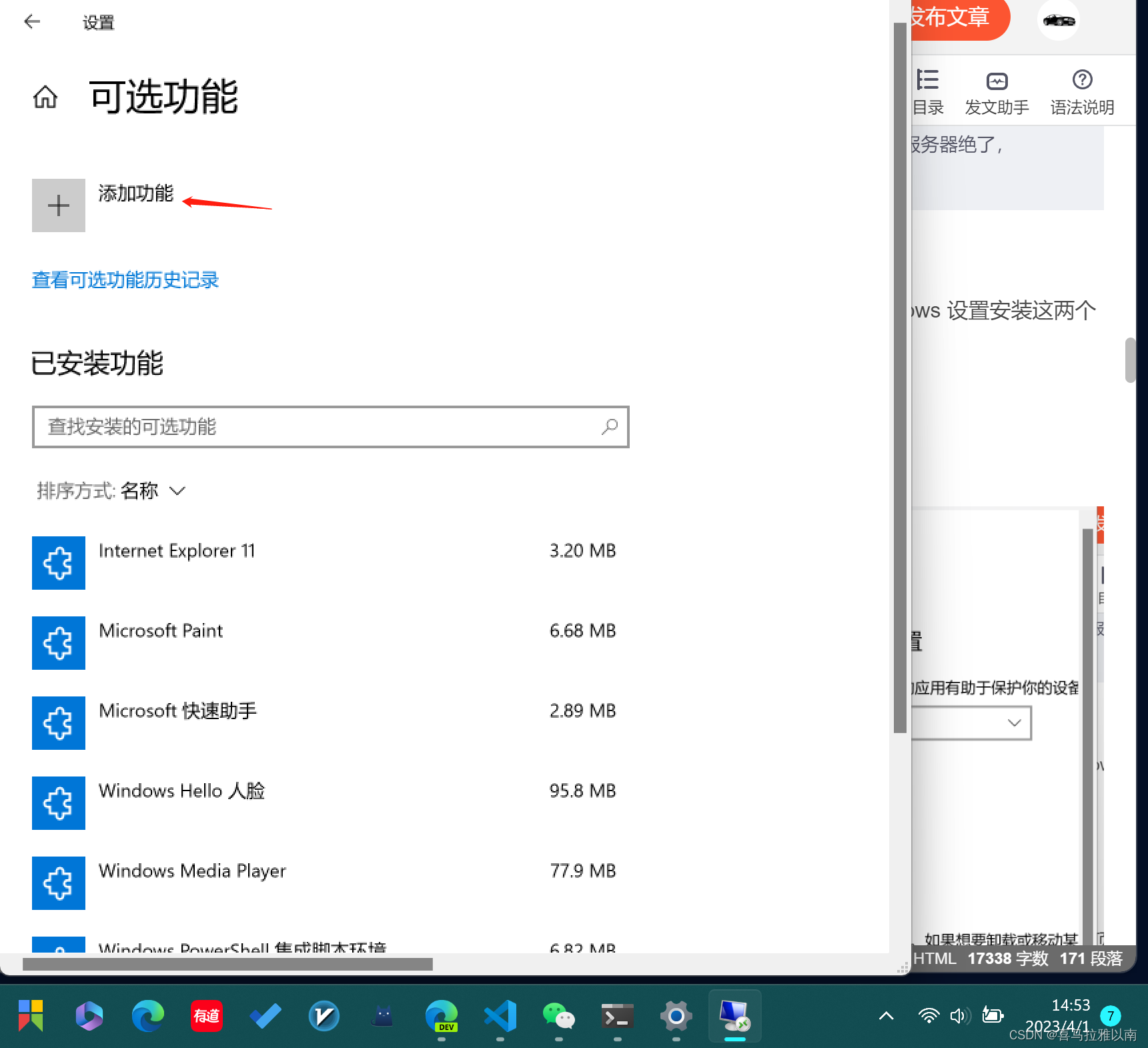
查找“OpenSSH 客户端”,再单击“安装”
查找“OpenSSH 服务器”,再单击“安装”
设置完成后,回到“应用”>“应用和功能”和“可选功能”,你应会看到已列出 OpenSSH
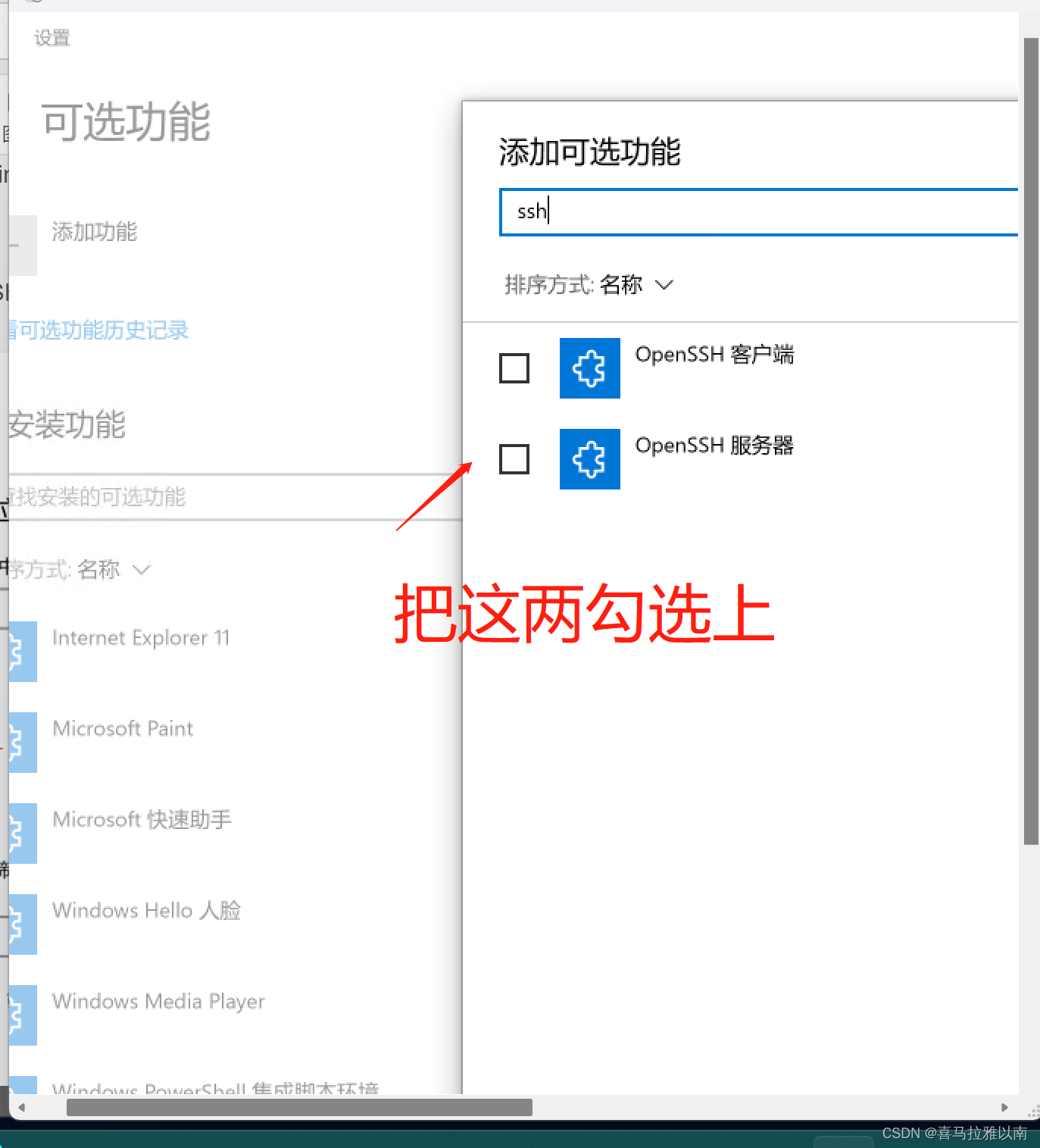
这种安装方法其实和ps脚本在线安装差不多,但这种安装貌似不支持同时安装sftp这种工具,并且安装可能还会失败(可能是受到网络限制)。
ps脚本在线安装
这个安装方式就很简单了,不过要使用这种安装方式必须检查电脑上是否支持Get-WindowsCapability这种powershell命令,一般Windows10机器都是支持的,问题不大,笔者是Win11必然没问题,就挺酷hhh
微软官方参考
打开Powershell,或者再CMD中执行一下下powershell,使终端中激活Powershell环境。
Get-WindowsCapability -Online | Where-Object Name -like 'OpenSSH*'
如果你客户端和服务端都没有安装,则会出现
Name : OpenSSH.Client~~~~0.0.1.0
State : NotPresentName : OpenSSH.Server~~~~0.0.1.0
State : NotPresent
然后,根据需要安装服务器或客户端组件:
# Install the OpenSSH Client
Add-WindowsCapability -Online -Name OpenSSH.Client~~~~0.0.1.0# Install the OpenSSH Server
Add-WindowsCapability -Online -Name OpenSSH.Server~~~~0.0.1.0
安装过程中会出现如下图的进度条,反正……慢的很
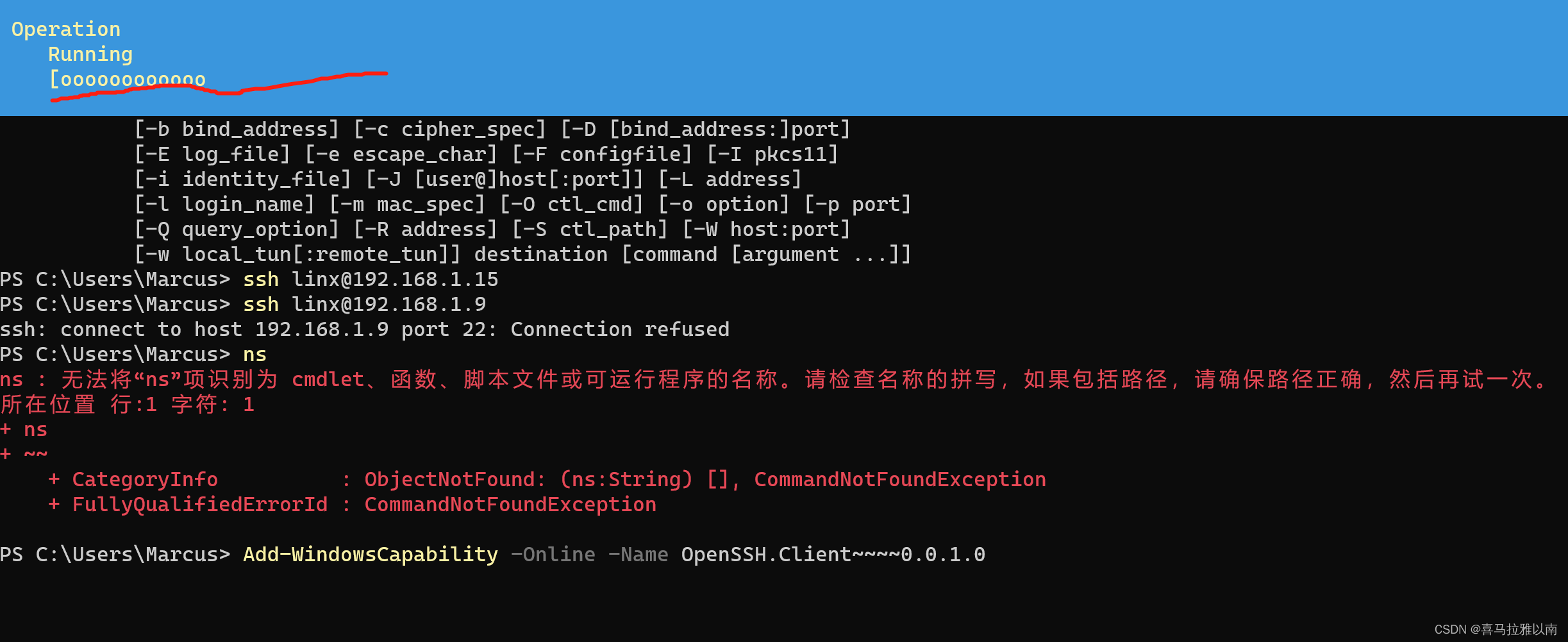
无论Client还是Server安装好后都会出现,这样就算安装好了。
Path :
Online : True
RestartNeeded : False
ps脚本离线安装
这个安装就需要先去github下载release的制品,点击右侧release
选择符合你版本的zip文件,我选择的是OpenSSH-Win64.zip
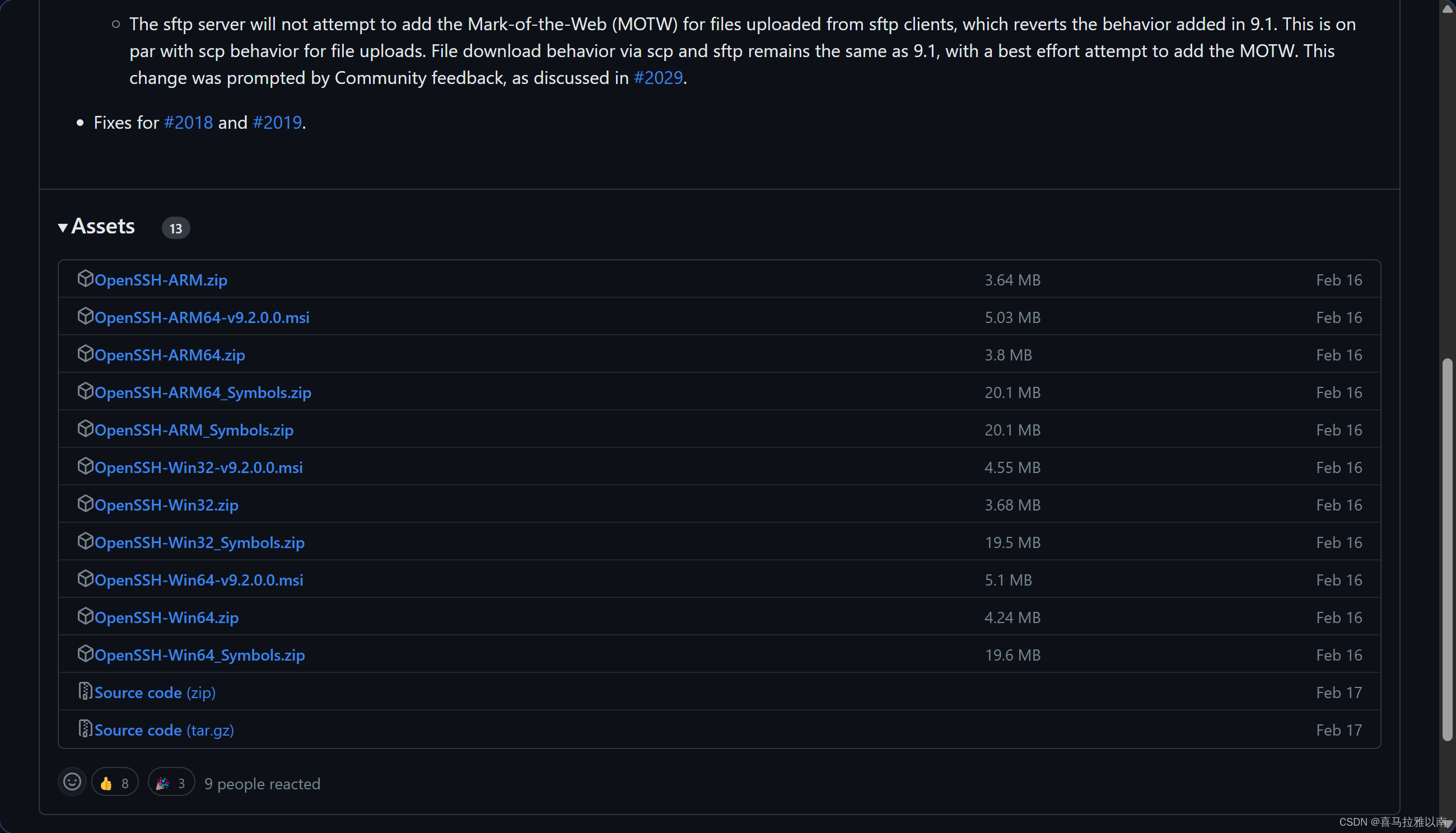
下载好后放到你期望的目录下解压,并进入Terminal。
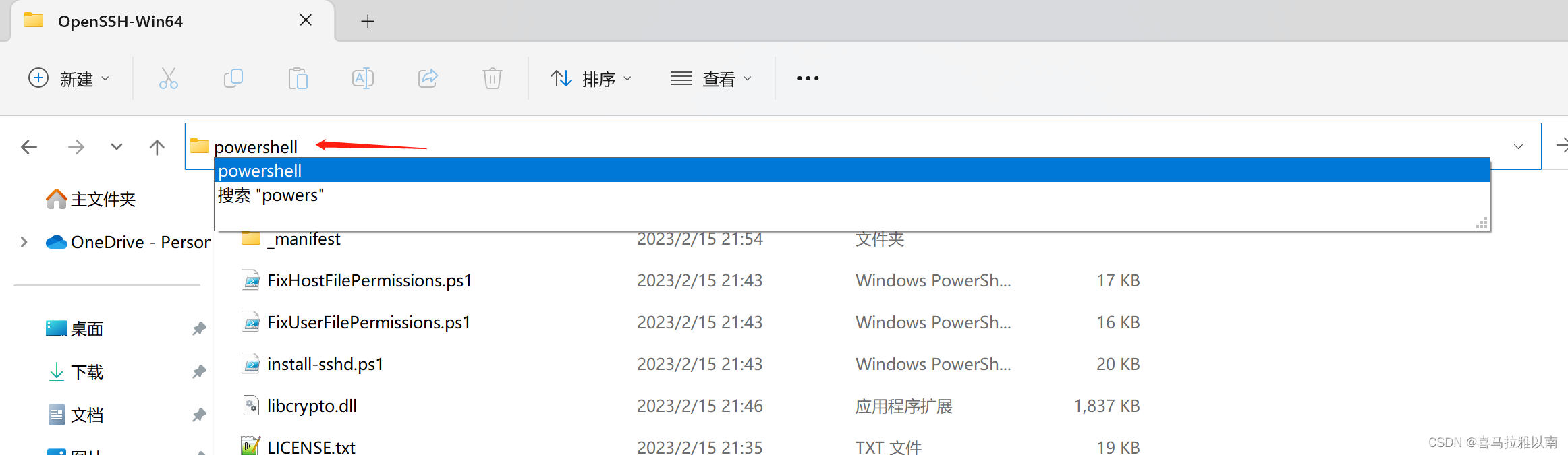
在终端执行install-sshd.ps1,执行安装脚本,此处执行一定要是管理员身份!!
打开install-sshd.ps1脚本我们就可以看到,其实是主要是将目录中的一些exe文件注册到了服务列表中,并将其添加到了机器变量中。
New-Service -Name sshd -DisplayName "OpenSSH SSH Server" -BinaryPathName "$sshdpath" -Description $sshdDesc -StartupType Manual | Out-Null
最后我们看到如下就算安装成功了
sshd and ssh-agent services successfully installed
如果需要在防火墙中添加入栈规则,执行如下命令,这样别人访问你机器的22端口就不会被拦截了
New-NetFirewallRule -Name sshd -DisplayName 'OpenSSH Server (sshd)' -Enabled True -Direction Inbound -Protocol TCP -Action Allow -LocalPort 22
其他二进制安装包安装
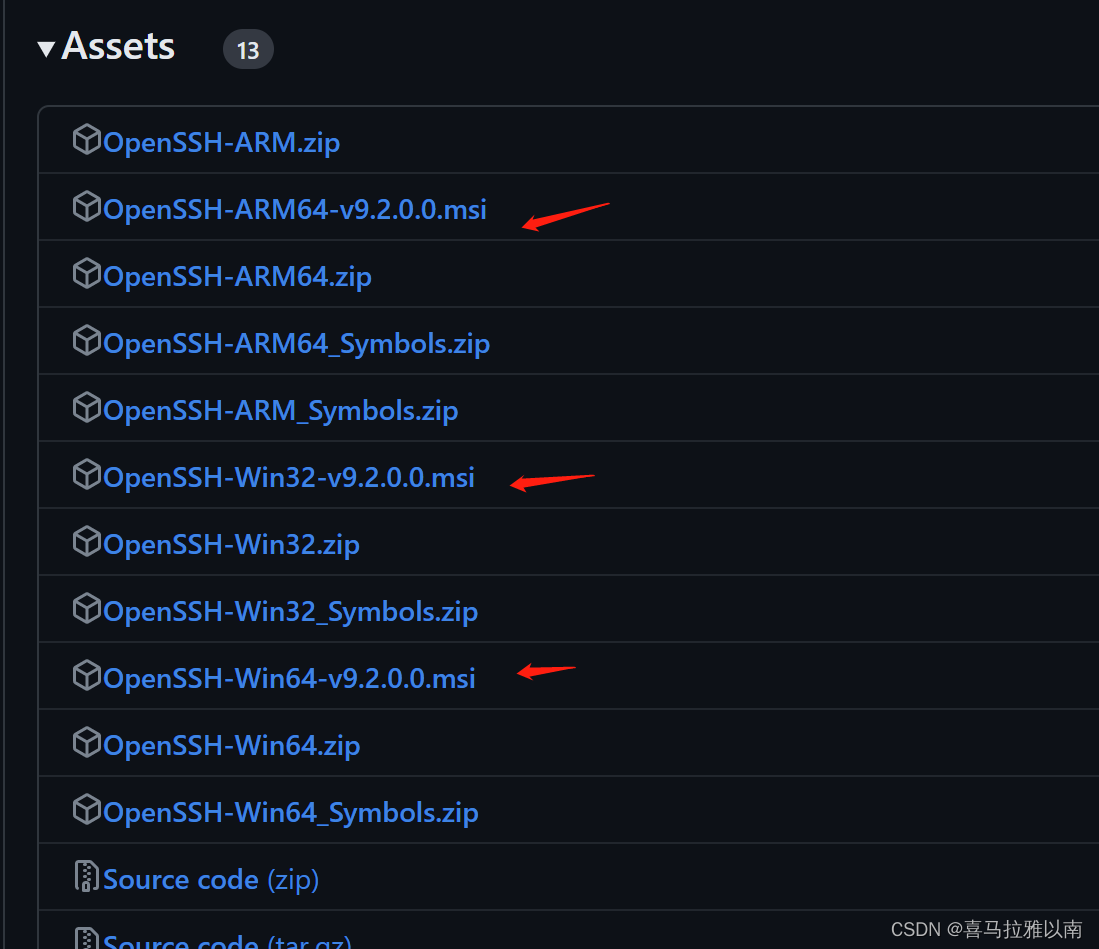
二进制安装就是指安装包一键安装,也是在GitHub下载,下载msi后缀的就可以了,根据自己电脑的cpu指令集架构下载就行。
相关文章:

Windows机器安装SSH搭建,自己搞个局域网机房玩一玩
Windows机器安装SSH搭建为啥要装SSH安装OpenSSH使用 Windows 设置来安装 OpenSSHps脚本在线安装ps脚本离线安装其他二进制安装包安装为啥要装SSH 家里有多台Win机器,一台主机两个笔记本,本着不浪费的原则,打算把它们在平时的工作学习中利用起…...
二叉树的前序遍历(力扣144)
目录 题目描述: 解法一:递归法 解法二:迭代法 解法三:Morris 遍历 二叉树的前序遍历 题目描述: 给你二叉树的根节点 root ,返回它节点值的 前序 遍历。 示例 1: 输入:root […...
【数据库管理】①实例与数据库
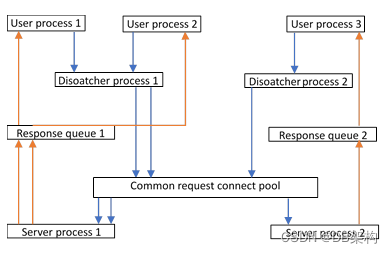
1.Oracle RDBMS 架构图 2. Oracle 体系结构 由此区分database和instance的区别 No.1.oracle serverdatabase instance2.databasedata file、control file、redo log file3.instancean instance accesses a database4.oracle memorySGA PGA(oracle的内存结构)5.instanceSGA …...
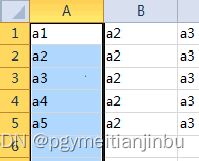
vba:单元格的选择,查找,合并,批注,SpecialCells,图形插入
一: 活动单元格:activecell,工作表中活动单元格只有一个 Sub activecells() a activecell.Address 取得活动单元格地址 Cells(2, 3).Activate 激活指定单元格 End Sub selection光标所选区域 Sub 光标所选区域() Selection 1 End Sub Sub …...
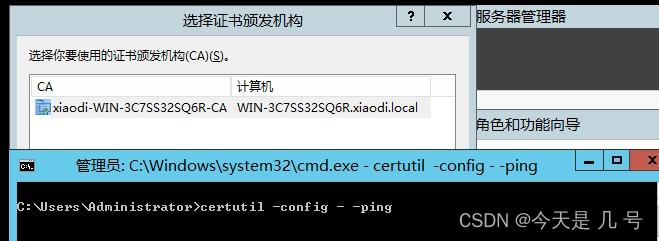
【内网安全】横向移动域控提权NetLogonADCSPACKDC永恒之蓝
文章目录章节点横向移动-系统漏洞-CVE-2017-0146(永恒之蓝)影响版本插件检测-横向移动CS联动MSF-检测&利用横向移动-域控提权-CVE-2014-6324横向移动-域控提权-CVE-2020-1472影响版本横向移动-域控提权-CVE-2021-42287前提条件影响版本python版本EXP利用过程C#版本EXP利用过…...
将本地项目上传到远程仓库的步骤
文章目录将本地项目上传到远程仓库的步骤1.进入想上传的项目文件夹2.初始化本地仓库3.添加该项目下的所有文件4.将文件添加到本地仓库中5.添加远程仓库6.将文件更新到远程仓库上7.将本地文件推送回到指定的远程仓库中将本地项目上传到远程仓库的步骤 1.进入想上传的项目文件夹…...

selenium+opencv实现模拟登陆(滑块验证码)
很多网站登录登陆时都要用到滑块验证码,在某些场景例如使用爬虫爬取信息时常常受到阻碍,想着用opencv的模板匹配试试能不能实现模拟登陆。本来觉得网上资料多应该还蛮容易,但实际上手还是搞了蛮久,在这里记录一下整个流程…...

辽宁申请互联网医院牌照流程
辽宁申请互联网医院牌照流程|沈阳市|大连市|鞍山市|抚顺市|本溪市|丹东市|锦州市|营口市|阜新市|辽阳市|盘锦市|铁岭市|朝阳市|葫芦岛市 很多的人对互联网医院都不是很了解,也不太清楚互联网医院牌照怎么申请,其实牌照申请每个地区都不太一样&#x…...

java实现布隆过滤器
什么是布隆过滤器 布隆过滤器(Bloom Filter)是1970年由布隆提出来的。 它实际上是由一个很长的二进制数组一系列hash算法映射函数,用于判断一个元素是否存在于集合中。 布隆过滤器可以用于检索一个元素是否在一个集合中。它的优点是空间效率和…...
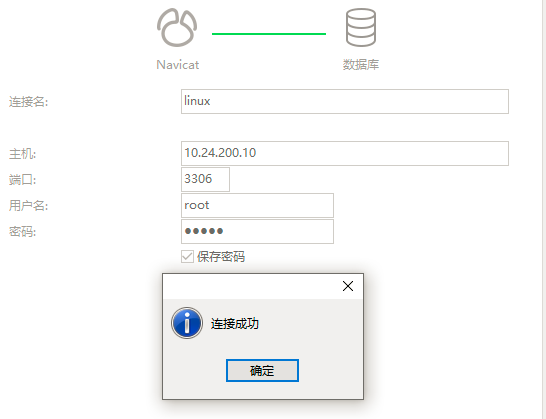
gitlab部署及整合Jenkins持续构建(三)nexus私服的安装及实战、linux安装mysql
文章目录敏捷持续集成是什么?linux安装jdk和maven安装jdk安装mavenlinux安装nexus3.xnexus私服的使用编译安装mysql可能遇到的问题使用cmake时报错敏捷持续集成是什么? 持续集成是一种软件开发实践,即团队开发成员经常集成他们的工作&#x…...
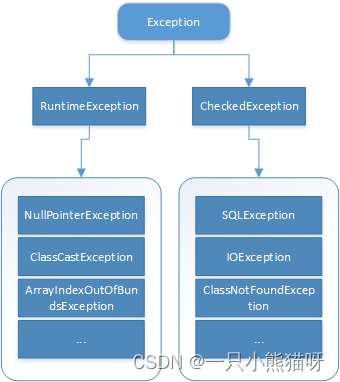
一、Java基础(2)
本章概要 异常的分类及处理 异常的概念异常的分类处理异常的方式 反射机制 动态语言的概念反射机制的概念反射的作用Java 的反射 API反射的过程创建对象的两种方式Method 的 invoke 方法 1.2 异常的分类及处理 1.2.1 异常的概念 异常指在方法不能按正常方式完成时…...

软件设计师重要知识点——第一章——计算机组成与体系结构
目录 1.1数据的表示 1.2数值表示范围 1.3浮点的运算 1.4计算机结构 1.5计算机体系结构分类——Flynn 1.6指令的基本概念 1.7寻址方式 1.8CISC与RISC 1.9流水线 1.10层次化存储结构 1.11Cache 1.12主存——编址与计算 1.13总线 1.14串联系统与并联系统 1.15N模混…...

编程学习心得
我来写一些,我关于编程的简单认识吧。 我觉得编程是一门艺术,也是一项技能,需要不断地学习和练习。无论是初学者还是有经验的开发人员,都需要耐心和恒心,才能够成为一名优秀的程序员。以下是一些关于编程学习的心得和…...

web获取媒体流
1. 下面例子演示了录屏和截图功能: <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta http-equiv"X-UA-Compatible" content"IEedge"><meta name"viewport"…...
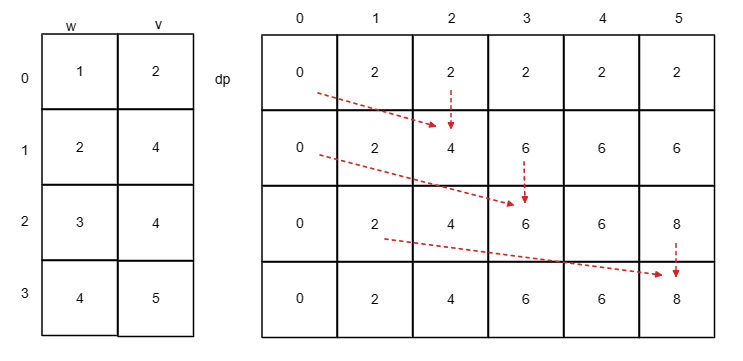
代码随想录算法训练营第四十二天 | 01背包问题,你该了解这些、01背包问题,你该了解这些 滚动数组、 416. 分割等和子集
打卡第42天,搞搞01背包。 今日任务 01背包问题,你该了解这些!01背包问题,你该了解这些! 滚动数组416.分割等和子集 背包问题1.0 :0-1 背包 有n件物品和一个最多能背重量为w 的背包。第i件物品的重量是weig…...

【Android】JNI静态与动态注册介绍
JNI的两种注册机制:静态注册和动态注册. 一、JNI介绍 JNI(Java Native Interface),即Java本地接口,JNI是Java调用Native 语言的一种特性。通过JNI可以使得Java与C/C机型交互. 方式: 静态注册动态注册:需要提供Java中…...

【算法题解】22. 接雨水
这是一道 困难 题 题目来自: https://leetcode.cn/problems/trapping-rain-water/ 题目 给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。 示例 1: 输入:height [0,…...
集合的遍历)
集合详解之(四)集合的遍历
文章目录🐒个人主页🏅JavaSE系列专栏📖前言:🎀ArrayList集合forEach()方法遍历🎀for循环遍历(针对List集合)🪅增强for循环(也支持Set集合)&#x…...
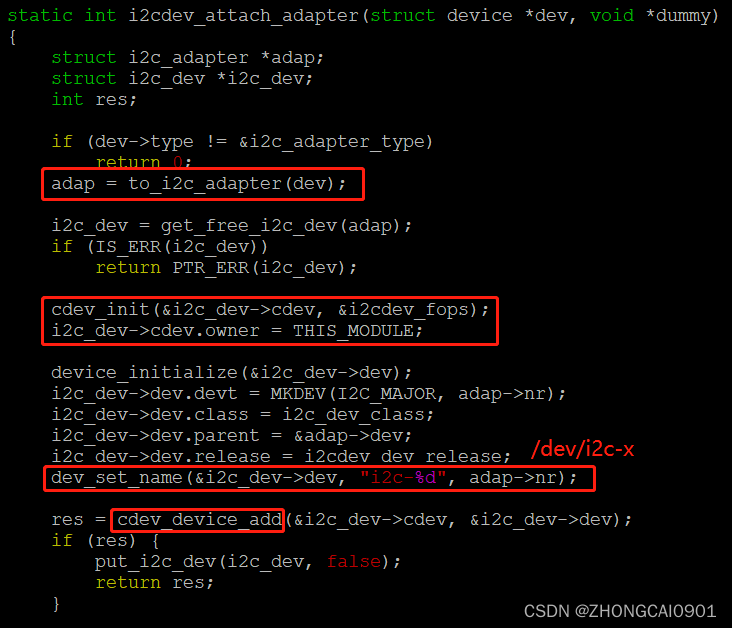
【I2C】通用驱动i2c-dev分析
文章目录1. 前言2. i2c-dev驱动的注册过程3. open_i2c_dev函数分析4. set_slave_addr函数分析5. i2c_read_bytes函数分析1. 前言 前面分析i2c-tool测试工具就是基于drivers/i2c/i2c-dev.c驱动来实现的。i2c-dev驱动在加载时会遍历所有的I2C总线(i2c_bus_type)上所有注册的adap…...

用GPT-4写代码不用翻墙了?Cursor告诉你:可以~~
目录 一、介绍 二、使用方法 三、其他实例 1.正则表达式 2.自动化测试脚本 3.聊聊技术 一、介绍 Cursor主要功能是根据用户的描述写代码或者进行对话,对话的范围仅限技术方面。优点是不用翻墙、不需要账号。Cursor基于GPT模型,具体什么版本不祥&#…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

CSS设置元素的宽度根据其内容自动调整
width: fit-content 是 CSS 中的一个属性值,用于设置元素的宽度根据其内容自动调整,确保宽度刚好容纳内容而不会超出。 效果对比 默认情况(width: auto): 块级元素(如 <div>)会占满父容器…...

Mysql中select查询语句的执行过程
目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析(Parser) 2.4、执行sql 1. 预处理(Preprocessor) 2. 查询优化器(Optimizer) 3. 执行器…...

C++:多态机制详解
目录 一. 多态的概念 1.静态多态(编译时多态) 二.动态多态的定义及实现 1.多态的构成条件 2.虚函数 3.虚函数的重写/覆盖 4.虚函数重写的一些其他问题 1).协变 2).析构函数的重写 5.override 和 final关键字 1&#…...

通过MicroSip配置自己的freeswitch服务器进行调试记录
之前用docker安装的freeswitch的,启动是正常的, 但用下面的Microsip连接不上 主要原因有可能一下几个 1、通过下面命令可以看 [rootlocalhost default]# docker exec -it freeswitch fs_cli -x "sofia status profile internal"Name …...

用鸿蒙HarmonyOS5实现中国象棋小游戏的过程
下面是一个基于鸿蒙OS (HarmonyOS) 的中国象棋小游戏的实现代码。这个实现使用Java语言和鸿蒙的Ability框架。 1. 项目结构 /src/main/java/com/example/chinesechess/├── MainAbilitySlice.java // 主界面逻辑├── ChessView.java // 游戏视图和逻辑├──…...

Visual Studio Code 扩展
Visual Studio Code 扩展 change-case 大小写转换EmmyLua for VSCode 调试插件Bookmarks 书签 change-case 大小写转换 https://marketplace.visualstudio.com/items?itemNamewmaurer.change-case 选中单词后,命令 changeCase.commands 可预览转换效果 EmmyLua…...

DAY 45 超大力王爱学Python
来自超大力王的友情提示:在用tensordoard的时候一定一定要用绝对位置,例如:tensorboard --logdir"D:\代码\archive (1)\runs\cifar10_mlp_experiment_2" 不然读取不了数据 知识点回顾: tensorboard的发展历史和原理tens…...
