二叉树的前序遍历(力扣144)
目录
题目描述:
解法一:递归法
解法二:迭代法
解法三:Morris 遍历
二叉树的前序遍历
题目描述:
给你二叉树的根节点 root ,返回它节点值的 前序 遍历。
示例 1:
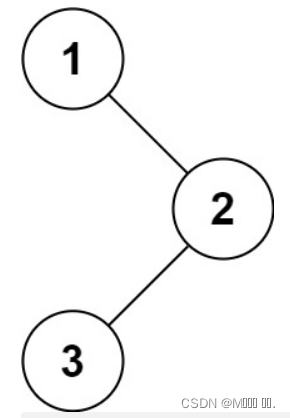
输入:root = [1,null,2,3] 输出:[1,2,3]
示例 2:
输入:root = [] 输出:[]
示例 3:
输入:root = [1] 输出:[1]
示例 4:
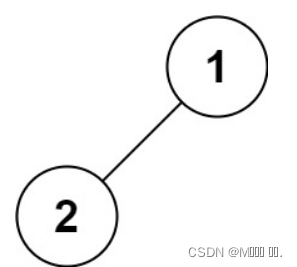
输入:root = [1,2] 输出:[1,2]
示例 5:
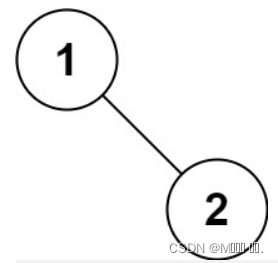
输入:root = [1,null,2] 输出:[1,2]
提示:
- 树中节点数目在范围
[0, 100]内 -100 <= Node.val <= 100
解法一:递归法
List<Integer> res = new ArrayList<>();public List<Integer> preorderTraversal(TreeNode root) {if(root == null){return res;}res.add(root.val);preorderTraversal(root.left);preorderTraversal(root.right);return res;}复杂度分析
- 时间复杂度:O(n)O(n),其中 nn 是二叉树的节点数。每一个节点恰好被遍历一次。
- 空间复杂度:O(n)O(n),为递归过程中栈的开销,平均情况下为 O(\log n)O(logn),最坏情况下树呈现链状,为 O(n)O(n)。
解法二:迭代法
public List<Integer> preorderTraversal(TreeNode root) {List<Integer> res = new ArrayList<>();if(root == null){return res;}Deque<TreeNode> stack = new ArrayDeque<>();stack.push(root);while(!stack.isEmpty()){TreeNode temp = stack.pop();res.add(temp.val);if(temp.right != null){stack.push(temp.right);}if(temp.left != null){stack.push(temp.left);}}return res;}复杂度分析
- 时间复杂度:O(n)O(n),其中 nn 是二叉树的节点数。每一个节点恰好被遍历一次。
- 空间复杂度:O(n)O(n),为迭代过程中显式栈的开销,平均情况下为 O(\log n)O(logn),最坏情况下树呈现链状,为 O(n)O(n)。
解法三:Morris 遍历
public List<Integer> preorderTraversal(TreeNode root) {List<Integer> res = new ArrayList<Integer>();if (root == null) {return res;}TreeNode p1 = root, p2 = null;while (p1 != null) {p2 = p1.left;if (p2 != null) {while (p2.right != null && p2.right != p1) {p2 = p2.right;}if (p2.right == null) {res.add(p1.val);p2.right = p1;p1 = p1.left;continue;} else {p2.right = null;}} else {res.add(p1.val);}p1 = p1.right;}return res;}
复杂度分析
- 时间复杂度:O(n)O(n),其中 nn 是二叉树的节点数。没有左子树的节点只被访问一次,有左子树的节点被访问两次。
- 空间复杂度:O(1)O(1)。只操作已经存在的指针(树的空闲指针),因此只需要常数的额外空间。
相关文章:

二叉树的前序遍历(力扣144)
目录 题目描述: 解法一:递归法 解法二:迭代法 解法三:Morris 遍历 二叉树的前序遍历 题目描述: 给你二叉树的根节点 root ,返回它节点值的 前序 遍历。 示例 1: 输入:root […...
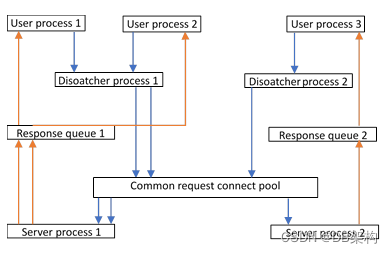
【数据库管理】①实例与数据库
1.Oracle RDBMS 架构图 2. Oracle 体系结构 由此区分database和instance的区别 No.1.oracle serverdatabase instance2.databasedata file、control file、redo log file3.instancean instance accesses a database4.oracle memorySGA PGA(oracle的内存结构)5.instanceSGA …...
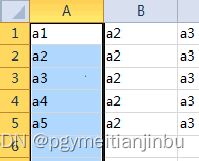
vba:单元格的选择,查找,合并,批注,SpecialCells,图形插入
一: 活动单元格:activecell,工作表中活动单元格只有一个 Sub activecells() a activecell.Address 取得活动单元格地址 Cells(2, 3).Activate 激活指定单元格 End Sub selection光标所选区域 Sub 光标所选区域() Selection 1 End Sub Sub …...
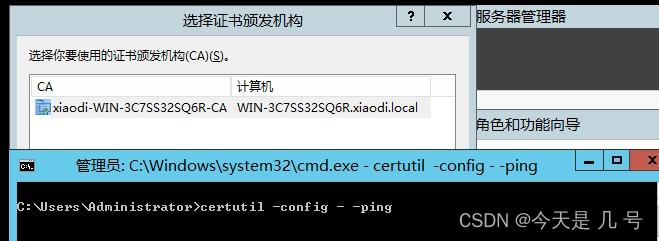
【内网安全】横向移动域控提权NetLogonADCSPACKDC永恒之蓝
文章目录章节点横向移动-系统漏洞-CVE-2017-0146(永恒之蓝)影响版本插件检测-横向移动CS联动MSF-检测&利用横向移动-域控提权-CVE-2014-6324横向移动-域控提权-CVE-2020-1472影响版本横向移动-域控提权-CVE-2021-42287前提条件影响版本python版本EXP利用过程C#版本EXP利用过…...
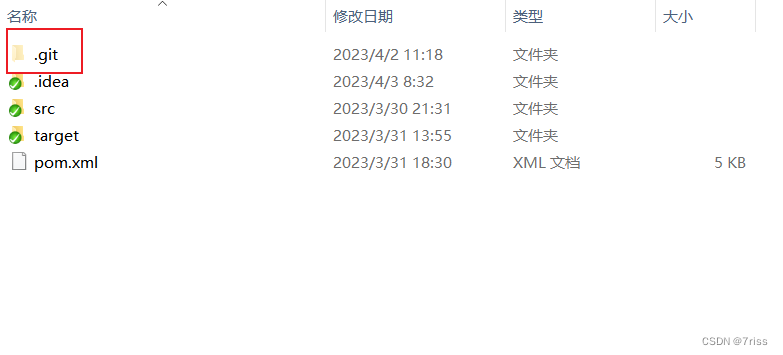
将本地项目上传到远程仓库的步骤
文章目录将本地项目上传到远程仓库的步骤1.进入想上传的项目文件夹2.初始化本地仓库3.添加该项目下的所有文件4.将文件添加到本地仓库中5.添加远程仓库6.将文件更新到远程仓库上7.将本地文件推送回到指定的远程仓库中将本地项目上传到远程仓库的步骤 1.进入想上传的项目文件夹…...

selenium+opencv实现模拟登陆(滑块验证码)
很多网站登录登陆时都要用到滑块验证码,在某些场景例如使用爬虫爬取信息时常常受到阻碍,想着用opencv的模板匹配试试能不能实现模拟登陆。本来觉得网上资料多应该还蛮容易,但实际上手还是搞了蛮久,在这里记录一下整个流程…...

辽宁申请互联网医院牌照流程
辽宁申请互联网医院牌照流程|沈阳市|大连市|鞍山市|抚顺市|本溪市|丹东市|锦州市|营口市|阜新市|辽阳市|盘锦市|铁岭市|朝阳市|葫芦岛市 很多的人对互联网医院都不是很了解,也不太清楚互联网医院牌照怎么申请,其实牌照申请每个地区都不太一样&#x…...

java实现布隆过滤器
什么是布隆过滤器 布隆过滤器(Bloom Filter)是1970年由布隆提出来的。 它实际上是由一个很长的二进制数组一系列hash算法映射函数,用于判断一个元素是否存在于集合中。 布隆过滤器可以用于检索一个元素是否在一个集合中。它的优点是空间效率和…...
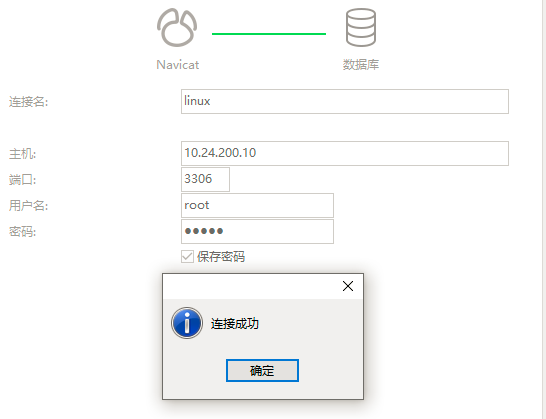
gitlab部署及整合Jenkins持续构建(三)nexus私服的安装及实战、linux安装mysql
文章目录敏捷持续集成是什么?linux安装jdk和maven安装jdk安装mavenlinux安装nexus3.xnexus私服的使用编译安装mysql可能遇到的问题使用cmake时报错敏捷持续集成是什么? 持续集成是一种软件开发实践,即团队开发成员经常集成他们的工作&#x…...
一、Java基础(2)
本章概要 异常的分类及处理 异常的概念异常的分类处理异常的方式 反射机制 动态语言的概念反射机制的概念反射的作用Java 的反射 API反射的过程创建对象的两种方式Method 的 invoke 方法 1.2 异常的分类及处理 1.2.1 异常的概念 异常指在方法不能按正常方式完成时…...

软件设计师重要知识点——第一章——计算机组成与体系结构
目录 1.1数据的表示 1.2数值表示范围 1.3浮点的运算 1.4计算机结构 1.5计算机体系结构分类——Flynn 1.6指令的基本概念 1.7寻址方式 1.8CISC与RISC 1.9流水线 1.10层次化存储结构 1.11Cache 1.12主存——编址与计算 1.13总线 1.14串联系统与并联系统 1.15N模混…...

编程学习心得
我来写一些,我关于编程的简单认识吧。 我觉得编程是一门艺术,也是一项技能,需要不断地学习和练习。无论是初学者还是有经验的开发人员,都需要耐心和恒心,才能够成为一名优秀的程序员。以下是一些关于编程学习的心得和…...

web获取媒体流
1. 下面例子演示了录屏和截图功能: <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta http-equiv"X-UA-Compatible" content"IEedge"><meta name"viewport"…...
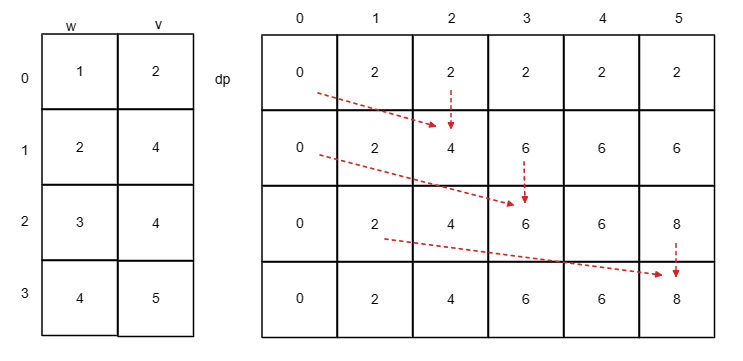
代码随想录算法训练营第四十二天 | 01背包问题,你该了解这些、01背包问题,你该了解这些 滚动数组、 416. 分割等和子集
打卡第42天,搞搞01背包。 今日任务 01背包问题,你该了解这些!01背包问题,你该了解这些! 滚动数组416.分割等和子集 背包问题1.0 :0-1 背包 有n件物品和一个最多能背重量为w 的背包。第i件物品的重量是weig…...

【Android】JNI静态与动态注册介绍
JNI的两种注册机制:静态注册和动态注册. 一、JNI介绍 JNI(Java Native Interface),即Java本地接口,JNI是Java调用Native 语言的一种特性。通过JNI可以使得Java与C/C机型交互. 方式: 静态注册动态注册:需要提供Java中…...

【算法题解】22. 接雨水
这是一道 困难 题 题目来自: https://leetcode.cn/problems/trapping-rain-water/ 题目 给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。 示例 1: 输入:height [0,…...
集合的遍历)
集合详解之(四)集合的遍历
文章目录🐒个人主页🏅JavaSE系列专栏📖前言:🎀ArrayList集合forEach()方法遍历🎀for循环遍历(针对List集合)🪅增强for循环(也支持Set集合)&#x…...
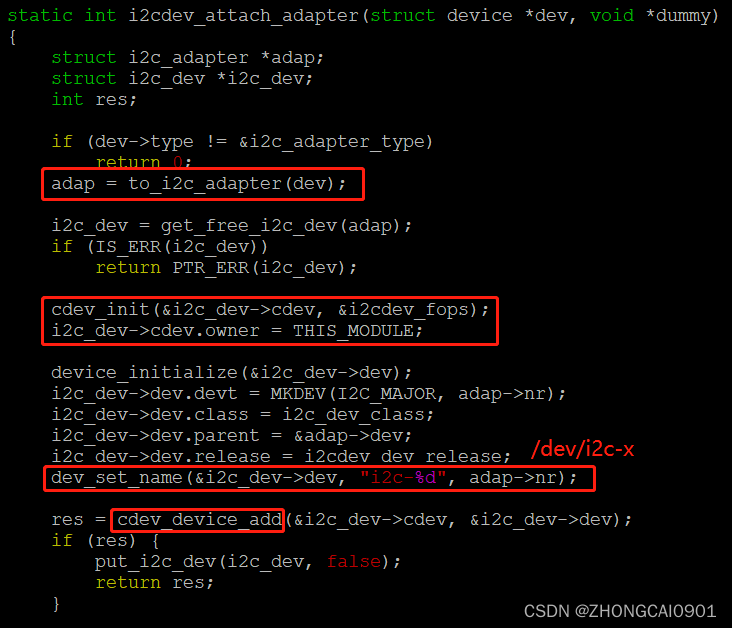
【I2C】通用驱动i2c-dev分析
文章目录1. 前言2. i2c-dev驱动的注册过程3. open_i2c_dev函数分析4. set_slave_addr函数分析5. i2c_read_bytes函数分析1. 前言 前面分析i2c-tool测试工具就是基于drivers/i2c/i2c-dev.c驱动来实现的。i2c-dev驱动在加载时会遍历所有的I2C总线(i2c_bus_type)上所有注册的adap…...

用GPT-4写代码不用翻墙了?Cursor告诉你:可以~~
目录 一、介绍 二、使用方法 三、其他实例 1.正则表达式 2.自动化测试脚本 3.聊聊技术 一、介绍 Cursor主要功能是根据用户的描述写代码或者进行对话,对话的范围仅限技术方面。优点是不用翻墙、不需要账号。Cursor基于GPT模型,具体什么版本不祥&#…...

硬件语言Verilog HDL牛客刷题day03 时序逻辑部分
1.VL21 根据状态转移表实现时序电路 1.题目: 某同步时序电路转换表如下,请使用D触发器和必要的逻辑门实现此同步时序电路,用Verilog语言描述。 2.解题思路 2.1 首先同步时序电路 , 时钟上升沿触发, 复位信号rst 低电…...

基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统,利用大模型实现智能 UI 自动化,结合计算机视觉和自然语言处理技术,实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法:netstat [选项] 功能:查看网络状态 常用选项: n 拒绝显示别名&#…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...

html-<abbr> 缩写或首字母缩略词
定义与作用 <abbr> 标签用于表示缩写或首字母缩略词,它可以帮助用户更好地理解缩写的含义,尤其是对于那些不熟悉该缩写的用户。 title 属性的内容提供了缩写的详细说明。当用户将鼠标悬停在缩写上时,会显示一个提示框。 示例&#x…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...

JS手写代码篇----使用Promise封装AJAX请求
15、使用Promise封装AJAX请求 promise就有reject和resolve了,就不必写成功和失败的回调函数了 const BASEURL ./手写ajax/test.jsonfunction promiseAjax() {return new Promise((resolve, reject) > {const xhr new XMLHttpRequest();xhr.open("get&quo…...
