代码随想录算法训练营第四十二天 | 01背包问题,你该了解这些、01背包问题,你该了解这些 滚动数组、 416. 分割等和子集
打卡第42天,搞搞01背包。
今日任务
- 01背包问题,你该了解这些!
- 01背包问题,你该了解这些! 滚动数组
- 416.分割等和子集
背包问题1.0 :0-1 背包
有n件物品和一个最多能背重量为w 的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。每件物品只能用一次,求解将哪些物品装入背包里物品价值总和最大。
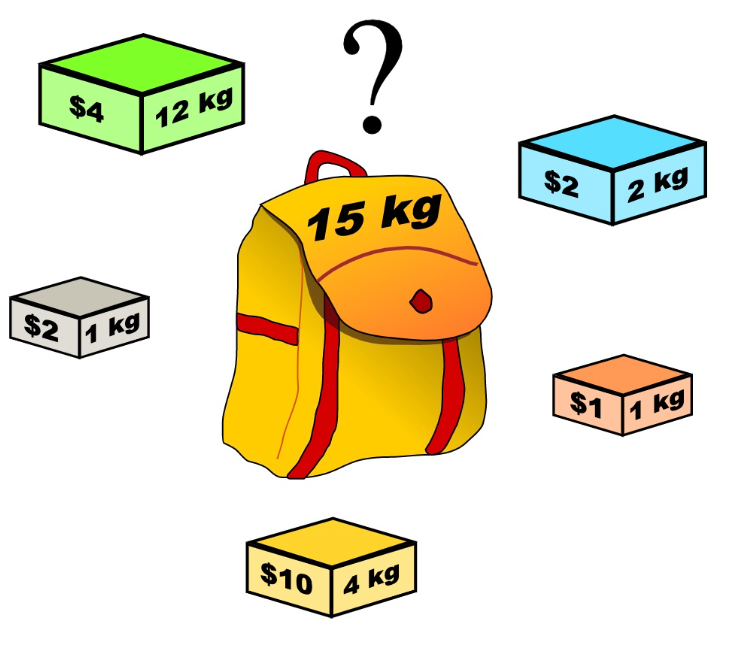
暴力的解法应该是怎么样的呢?
每一件物品其实只有两个状态,取或者不取,所以可以使用回溯法搜索出所有的情况,那么时间复杂度就是o(2n)o(2^n)o(2n),这里的n表示物品数量。
所以暴力的解法是指数级别的时间复杂度。进而才需要动态规划的解法来进行优化!
01背包
有 N 件物品和一个容量是 V 的背包。每件物品只能使用一次。
第 i 件物品的体积是 viv_ivi,价值是 wiw_iwi。
求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。
输出最大价值。
输入格式
第一行两个整数,N,V,用空格隔开,分别表示物品数量和背包容积。
接下来有 N 行,每行两个整数 viv_ivi,wiw_iwi,用空格隔开,分别表示第 i 件物品的体积和价值。
输出格式
输出一个整数,表示最大价值。
数据范围
0<N,V≤1000
0<viv_ivi,wiw_iwi≤1000
输入样例
4 5
1 2
2 4
3 4
4 5
输出样例:
8
代码随想录
-
确定 dp 以及下标定义
dp[i][j] 表示从下标为 [0-i] 的物品里任意取,放进容量为 j 的背包,价值总和最大是多少。
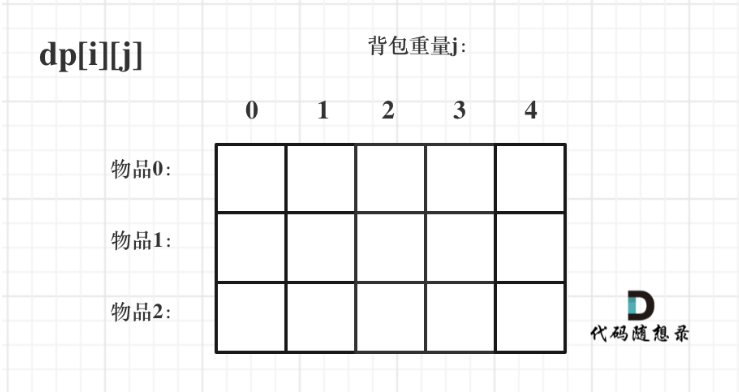
-
确定递推公式
两个方向推出来dp[i][j]不放物品i:由dp[i - 1][j]推出,即背包容量为j,里面不放物品i的最大价值,此时dp[i][j]就是dp[i - 1][j]。(其实就是当物品i的重量大于背包j的重量时,物品i无法放进背包中,所以被背包内的价值依然和前面相同。)
放物品i:由dp[i - 1][j - weight[i]]推出,dp[i - 1][j - weight[i]] 为背包容量为j - weight[i]的时候不放物品i的最大价值,那么dp[i - 1][j - weight[i]] + value[i] (物品i的价值),就是背包放物品i得到的最大价值
所以递归公式: dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
-
初始化
首先从dp[i][j]的定义出发,如果背包容量j为0的话,即dp[i][0],无论是选取哪些物品,背包价值总和一定为0。状态转移方程 dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]); 可以看出i 是由 i-1 推导出来,那么i为0的时候就一定要初始化。dp[0][j],即:i为0,存放编号0的物品的时候,各个容量的背包所能存放的最大价值。那么很明显当 j < weight[0]的时候,dp[0][j] 应该是 0,因为背包容量比编号0的物品重量还小。当j >= weight[0]时,dp[0][j] 应该是value[0],因为背包容量放足够放编号0物品。
-
确定遍历顺序
二维数组的情况下 先遍历背包跟先遍历重量都可以
一维数组的情况下 先遍历重量 -
推导
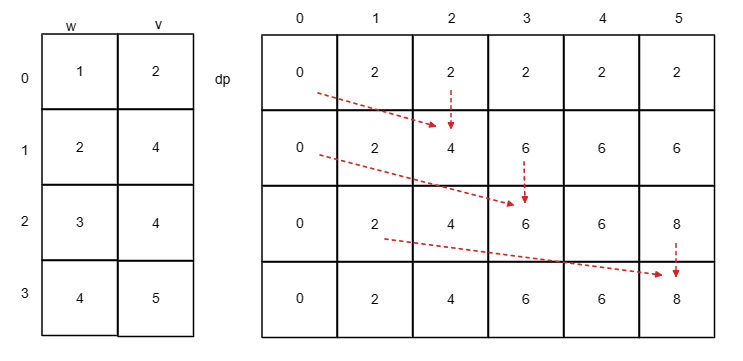
#include <bits/stdc++.h>using namespace std;int main() {int n, v;scanf("%d %d", &n, &v);vector<int> weight(n);vector<int> value(n);for(int i = 0; i < n; i++) {scanf("%d", &weight[i]);scanf("%d", &value[i]);}// 初始化vector<vector<int>> dp(n, vector<int>(v + 1, 0));for(int i = weight[0]; i <= v; i++) {dp[0][i] = value[0];}for(int i = 1; i < n; i++) {for(int j = 1; j <= v; j++) {if(j < weight[i]) dp[i][j] = dp[i - 1][j];else dp[i][j] = max(dp[i - 1][j - weight[i]] + value[i], dp[i - 1][j]);}}printf("%d", dp[n - 1][v]);return 0;
}
优化空间(滚动数组)
我们可以发现想知道dp[i][j] ,需要知道dp[i - 1][j - weight[i]] 和 dp[i - 1][j],都只是前一层的信息,所以我们可以用一个一维数组来保存信息,只不过我们的遍历顺序第一次遍历的是物品,第二层遍历的是背包,而且是从大到小遍历,因为想要知道大重量背包的最大价值总和,要知道前面的小重量背包的最大价值总和,而我们是用滚动数组保存,如果从小到大遍历,会改变小重量背包的最大价值总和。
#include <bits/stdc++.h>using namespace std;int main() {int n, v;scanf("%d %d", &n, &v);vector<int> weight(n);vector<int> value(n);for(int i = 0; i < n; i++) {scanf("%d", &weight[i]);scanf("%d", &value[i]);}// 初始化vector<int> dp(v + 1, 0);for(int i = weight[0]; i <= v; i++) {dp[i] = value[0];}for(int i = 1; i < n; i++) {for(int j = v; j >= 1; j--) {if(j < weight[i]) dp[j] = dp[j];else dp[j] = max(dp[j - weight[i]] + value[i], dp[j]);}}printf("%d", dp[v]);return 0;
}
416. 分割等和子集
给你一个 只包含正整数 的 非空 数组 nums 。请你判断是否可以将这个数组分割成两个子集,使得两个子集的元素和相等。
示例 1:
输入:nums = [1,5,11,5]
输出:true
解释:数组可以分割成 [1, 5, 5] 和 [11] 。
示例 2:
输入:nums = [1,2,3,5]
输出:false
解释:数组不能分割成两个元素和相等的子集。
提示:
1 <= nums.length <= 2001 <= nums[i] <= 100
我的题解
回溯暴力搜索,超时了哈哈哈
class Solution {
public:bool backtracking(vector<int>& nums, int sum, int starIndex) {if(sum == 0) return true;if(sum < 0) return false;for(int i = starIndex; i < nums.size(); i++) {sum -= nums[i];if(backtracking(nums, sum, i + 1)) return true;sum += nums[i];}return false;}bool canPartition(vector<int>& nums) {int sum = 0;for(int num : nums) sum += num;if(sum % 2 == 1) return false;sort(nums.begin(), nums.end());return backtracking(nums, sum / 2, 0);}
};
01背包做法,但是不是很理解。
class Solution {
public:bool canPartition(vector<int>& nums) {int sum = 0;for(int num : nums) sum += num;if(sum % 2 == 1) return false;vector<int> dp(sum / 2 + 1, 0);for(int i = nums[0]; i <= sum / 2; i++) dp[i] = nums[0]; // 初始化for(int i = 1; i < nums.size(); i++) {for(int j = sum / 2; j >= 1; j--) {if(j < nums[i]) dp[j] = dp[j];else dp[j] = max(dp[j - nums[i]] + nums[i], dp[j]);}}return dp[sum / 2] == sum / 2;}
};
代码随想录
class Solution {
public:bool canPartition(vector<int>& nums) {int sum = 0;// dp[i]中的i表示背包内总和// 题目中说:每个数组中的元素不会超过 100,数组的大小不会超过 200// 总和不会大于20000,背包最大只需要其中一半,所以10001大小就可以了vector<int> dp(10001, 0);for (int i = 0; i < nums.size(); i++) {sum += nums[i];}// 也可以使用库函数一步求和// int sum = accumulate(nums.begin(), nums.end(), 0);if (sum % 2 == 1) return false;int target = sum / 2;// 开始 01背包for(int i = 0; i < nums.size(); i++) {for(int j = target; j >= nums[i]; j--) { // 每一个元素一定是不可重复放入,所以从大到小遍历dp[j] = max(dp[j], dp[j - nums[i]] + nums[i]);}}// 集合中的元素正好可以凑成总和targetif (dp[target] == target) return true;return false;}
};
- 时间复杂度:O(n^2)
- 空间复杂度:O(n),虽然dp数组大小为一个常数,但是大常数
相关文章:

代码随想录算法训练营第四十二天 | 01背包问题,你该了解这些、01背包问题,你该了解这些 滚动数组、 416. 分割等和子集
打卡第42天,搞搞01背包。 今日任务 01背包问题,你该了解这些!01背包问题,你该了解这些! 滚动数组416.分割等和子集 背包问题1.0 :0-1 背包 有n件物品和一个最多能背重量为w 的背包。第i件物品的重量是weig…...

【Android】JNI静态与动态注册介绍
JNI的两种注册机制:静态注册和动态注册. 一、JNI介绍 JNI(Java Native Interface),即Java本地接口,JNI是Java调用Native 语言的一种特性。通过JNI可以使得Java与C/C机型交互. 方式: 静态注册动态注册:需要提供Java中…...

【算法题解】22. 接雨水
这是一道 困难 题 题目来自: https://leetcode.cn/problems/trapping-rain-water/ 题目 给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。 示例 1: 输入:height [0,…...
集合的遍历)
集合详解之(四)集合的遍历
文章目录🐒个人主页🏅JavaSE系列专栏📖前言:🎀ArrayList集合forEach()方法遍历🎀for循环遍历(针对List集合)🪅增强for循环(也支持Set集合)&#x…...
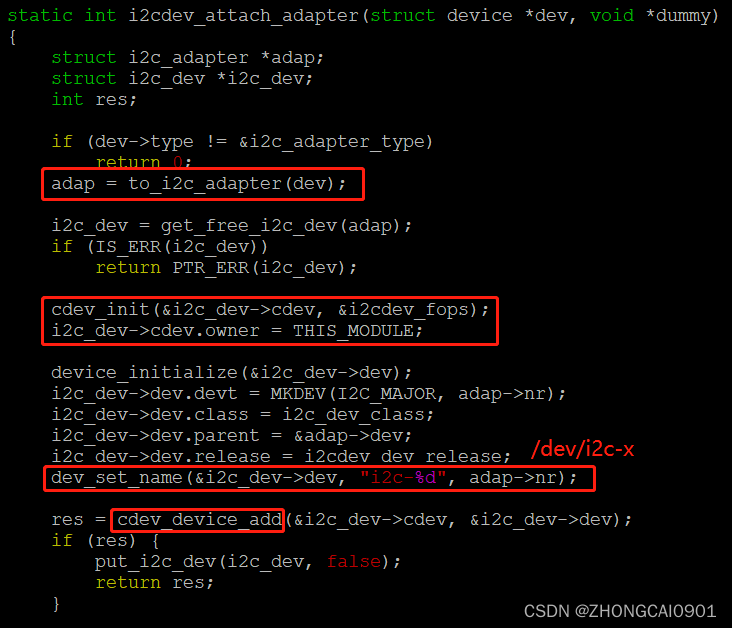
【I2C】通用驱动i2c-dev分析
文章目录1. 前言2. i2c-dev驱动的注册过程3. open_i2c_dev函数分析4. set_slave_addr函数分析5. i2c_read_bytes函数分析1. 前言 前面分析i2c-tool测试工具就是基于drivers/i2c/i2c-dev.c驱动来实现的。i2c-dev驱动在加载时会遍历所有的I2C总线(i2c_bus_type)上所有注册的adap…...

用GPT-4写代码不用翻墙了?Cursor告诉你:可以~~
目录 一、介绍 二、使用方法 三、其他实例 1.正则表达式 2.自动化测试脚本 3.聊聊技术 一、介绍 Cursor主要功能是根据用户的描述写代码或者进行对话,对话的范围仅限技术方面。优点是不用翻墙、不需要账号。Cursor基于GPT模型,具体什么版本不祥&#…...

硬件语言Verilog HDL牛客刷题day03 时序逻辑部分
1.VL21 根据状态转移表实现时序电路 1.题目: 某同步时序电路转换表如下,请使用D触发器和必要的逻辑门实现此同步时序电路,用Verilog语言描述。 2.解题思路 2.1 首先同步时序电路 , 时钟上升沿触发, 复位信号rst 低电…...

day31 ● 455.分发饼干 ● 376. 摆动序列 ● 53. 最大子序和
● 455.分发饼干 ● 376. 摆动序列 ● 53. 最大子序和 在本次的题目中,我们使用了贪心算法来解决三个问题:分发饼干、摆动序列、最大子序和。这三个问题都可以使用贪心算法来解决,而且贪心算法的时间复杂度相对较低,能够在较短的…...
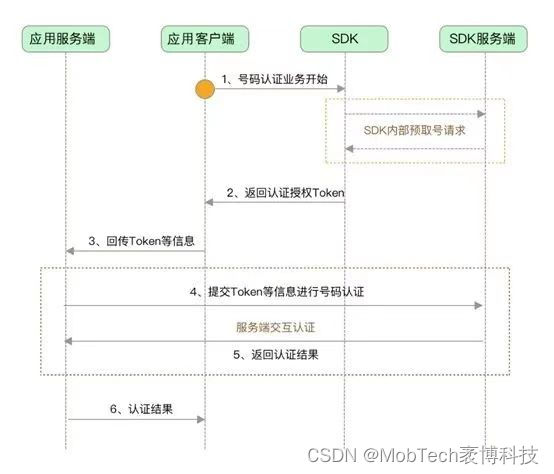
MobTech 秒验|本机号码一键登录会泄露隐私吗
本机号码一键登录是一种新型的应用登录方式,它可以利用运营商的数据网关认证能力,实现手机号免密登录,提高用户体验和转化率,降低验证成本和流失率。本机号码一键登录支持三大运营商号码认证,3秒内完成手机号验证&…...
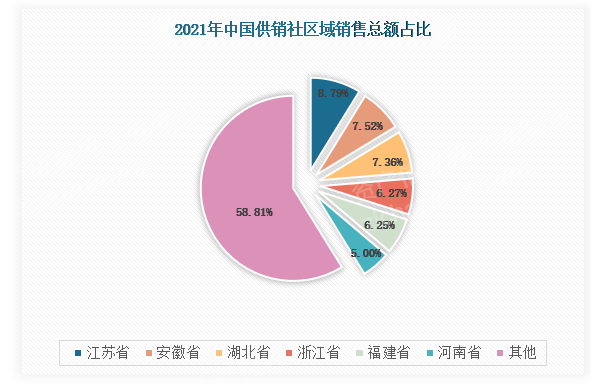
2023年供销合作社研究报告
第一章 行业概况 1.1 供销合作社概述 中华全国供销合作总社,是中华人民共和国全国供销合作社的联合组织。中华全国供销合作总社的前身可以追溯到1949年11月成立的中央合作事业管理局。在新中国成立初期,供销合作社就基本形成了自上而下、覆盖全国的组织…...
【ansible】实施任务控制
目录 实施任务控制 一,循环(迭代)--- loop 1,利用loop----item循环迭代任务 2,item---loop循环案例 1,定义item循环列表 2,通过变量应用列表格式 3,字典列表(迭代嵌套子…...

49天精通Java,第11天,java接口和抽象类的异同,default关键字
目录一、什么是接口二、接口的特点三、接口和类的区别四、接口和抽象类的区别五、接口的声明方式六、default默认方法大家好,我是哪吒。 一、什么是接口 Java接口是一系列方法的声明,是一些方法特征的集合,一个接口只有方法的特征没有方法的…...

JAVA练习99-逆波兰表达式求值
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 目录 前言 一、题目-逆波兰表达式求值 1.题目描述 2.思路与代码 2.1 思路 2.2 代码 总结 前言 提示:这里可以添加本文要记录的大概内容: 4月5…...
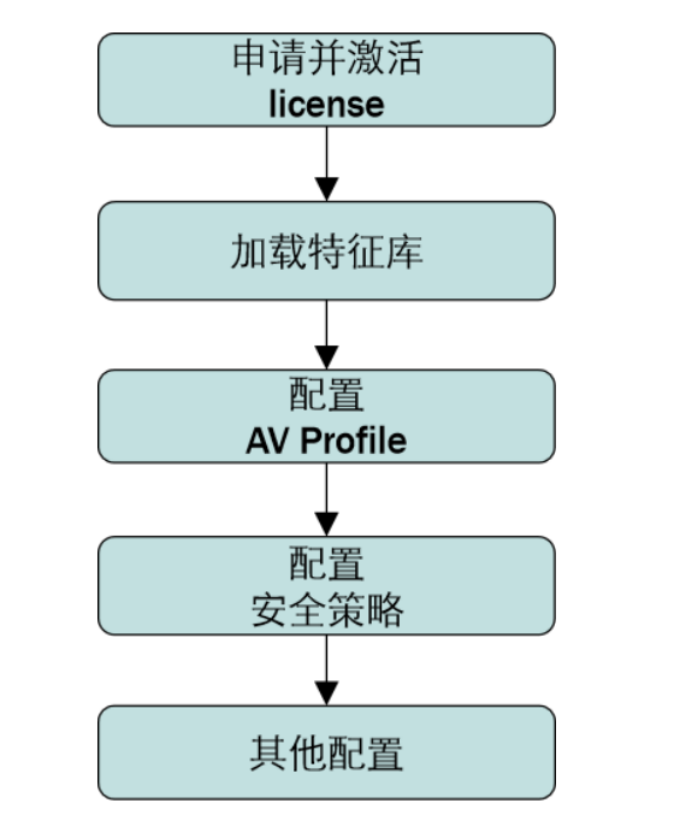
恶意软件、恶意软件反杀技术以及反病毒技术的详细介绍
1.恶意软件简单介绍恶意软件是指在计算机系统上执行恶意任务的病毒、蠕虫和特洛伊木马的程序,通过破坏软件进程来实施控制。腾讯移动安全实验室发布的数据显示,恶意软件由多种威胁组成,会不断弹出,所以需要采取多种方法和技术来进…...

【数据库运维】mysql备份恢复练习
目录 数据库备份,数据库为school,素材如下 1.创建student和score表 2.为student表和score表增加记录 3.备份数据库school到/backup目录 4.备份MySQL数据库为带删除表的格式,能够让该备份覆盖已有数据库而不需要手动删除原有数据库 5.直接将My…...

刷题30-对称的二叉树
对称的二叉树 思路:用递归,首先明白递归中止的条件是什么 搬用别人的看法: 做递归思考三步: 1.递归的函数要干什么? 函数的作用是判断传入的两个树是否镜像。 输入:TreeNode left, TreeNode right 输出…...

精选简历模板
1.应届生通用简历模板(.docx) 适用于应届生找工作的学生群体 https://download.csdn.net/download/weixin_43042683/87652099https://download.csdn.net/download/weixin_43042683/87652099 部分缩略图如下: 2.研究生通用简历模板(.docx)…...
蓝桥杯嵌入式第十三届客观题解析
文章目录 前言一、题目1二、题目2三、题目3四、题目4五、题目5六、题目6七、题目7八、题目8九、题目9十、题目10总结前言 本篇文章将带大家来学习蓝桥杯嵌入式的客观题了,蓝桥杯嵌入式的客观题涉及到模电,数电,单片机等知识,需要非常扎实的基础,客观题不能急于求成只能脚…...
【Redis】线程问题
文章目录单线程版本演化工作流程为什么逐渐又加入了多线程特性?影响Redis性能的主要因素->网络I/O多线程工作流程Unix网络编程中的五种I/O模型I/O多路复用工作原理:select、poll、epoll为什么Redis快单线程与多线程的比较配置文件开启多线程单线程 版本演化 Re…...

【算法题】2498. 青蛙过河 II
题目: 给你一个下标从 0 开始的整数数组 stones ,数组中的元素 严格递增 ,表示一条河中石头的位置。 一只青蛙一开始在第一块石头上,它想到达最后一块石头,然后回到第一块石头。同时每块石头 至多 到达 一次。 一次…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

今日学习:Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存
文章目录 优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义 使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因 常见解决方法更好的解决方法设计精妙之处 登录续期登录续期常见实现方式特…...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...

CVE-2020-17519源码分析与漏洞复现(Flink 任意文件读取)
漏洞概览 漏洞名称:Apache Flink REST API 任意文件读取漏洞CVE编号:CVE-2020-17519CVSS评分:7.5影响版本:Apache Flink 1.11.0、1.11.1、1.11.2修复版本:≥ 1.11.3 或 ≥ 1.12.0漏洞类型:路径遍历&#x…...
集成 Mybatis-Plus 和 Mybatis-Plus-Join)
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join 1、依赖1.1、依赖版本1.2、pom.xml 2、代码2.1、SqlSession 构造器2.2、MybatisPlus代码生成器2.3、获取 config.yml 配置2.3.1、config.yml2.3.2、项目配置类 2.4、ftl 模板2.4.1、…...
