23年408数据结构
第一题:
解析:
第一点,我们要知道顺序存储的特点:优点就是随用随取,就是你想要查询第几个元素可以直接查询出来,时间复杂度就是O(1),缺点就是不适合删除和插入,因为每次删除和插入一个元素之后都可能需要调整剩下的元素,因此时间复杂度不确定[最好情况下是O(1),最坏情况下是O(n),平均时间复杂度是O(n)]。由此可知,在顺序表中,查询(也就是获取)第i个元素的平均时间复杂度是O(1)。选项D对,且直接排除B,C,最后在来看一看A选项:在顺序表中查找一个指定值的元素,可能需要遍历整个数组,因此时间复杂度是O(n)。选项A错。
答案选D。
第二题:
解析:注意题目说的是一个双向链表,该题考察的是双向链表的插入,这种题就是要画图。
在执行题目给的语句之后,结点p(p指针所指向的结点简称结点p,后面的同理)的next指针指向结点s,结点s的next指针指向结点q。因为是双向链表,还缺一个结点s到结点p的指针,结点q到结点s的指针。因为链表有一个特点就是未知的结点我们要用已知的指针表示出来不能直接使用,就比如这个结点q,在执行语句中并没有出现q指针,因此结点q就是未知的,先看一下结点q怎么给它表示出来:s->next=q,下图就是执行完语句之后的样子。
1.此时还缺一条结点s指向结点p的指针,观察图:结点s是已知的,怎么找到结点p?因为此时只有图中的三根指针,想找到结点p只能s->next->prev=p,
结点s到结点p的指针:s->prev=p,而p=s->next->prev,合并一下:s->prev=s->next->prev。
2.因为此时结点q的前指针prev还指向的p,我们应该把这个指针调整成指向s。
因此结点q到结点s的指针:q->prev=s,而s->next=q,合并一下也就是s->next->prev=s。
这题不难,就是要注意是双向链表,以及要细心留意一下有哪些指针和怎么用已有的指针来表示出各种结点。这是结点s插入完成的样子,可以对比着看一下。
答案选C
第三题:
解析:这个题的话你要知道三元组表是什么,三元组表储存了矩阵中关键字所在的行,列已经具体的值。三元组表储存稀疏矩阵时是不储存0的,只储存非零常数。因此你并不需要保存M中包含非零元素的行列数,因为只储存非零常数,而行和列同样能看到,数一下就行了,我们只还需要知道M的行数和列数就能将稀疏矩阵M还原出来了,就给非零常数填上去,其他位置添0就完了。
答案选A。
第四题:
解析:考察加权平均长度的计算方法:加权平均长度=带权路径长度/所有结点频次之和
第一步:构造哈夫曼树:
第二步:计算哈夫曼树带权平均长度:就是在带权路径长度的基础上再除一个所有频次之和。
答案选B。
第五题:
解析:这种题就你看这个结点的序列顺序,然后依次把字母添上去就行,最后是这个样子:
,然后根据这个图把前序序列写出来就行。
答案选A。
第六题:
解析:这个考察单源最短路径算法,我们说单源最短路径就是求一个点到另一个点的最短路径。而单源最短路径包括BFS算法和迪杰斯特拉算法,这两个算法都没有出现在题目当中,再来看看1,2。1,2是用来构造最小生成树的,边都变少了,显然不能求某点到其余顶点的最短路径,下面来看看3,广度优先搜索算法是从点一层一层往外拓展然后进行搜索的,越往外的顶点距离该点的距离越远,所以3是对的。
答案选C。
第七题:
解析:这题很奇怪,把终端结点当成了叶子结点。
1:插入操作可能增加树的高度:考察B树的插入。1对。
2:若被删结点是叶结点,显然会导致叶结点的变化:若被删结点不是叶结点,则要先将被删结点和它的前驱或后继交换,最终转换为删除叶结点,还是会导致叶结点的变化,Ⅱ正确。
3:如果在非叶结点中查找到了给定关:键字,则不用向下继续查找,Ⅲ错误。
4:插入关键字的初始位置是最底层叶结点,但可能因结点分裂而被转移到父结点中,IV错误。
答案选B。
第八题:
解析:
第一次折半:300
第二次折半:150
第三次折半:75
第四次折半:38(37 1 37注意第38元素左边37个元素,右边37个元素,因此下次折半的个数是37+1=38)
第五次折半:19(9 1 9注意第10元素左边9个元素,右边9个元素,因此下次折半的个数是9+1=10)
第六次折半:10
第七次折半:5(2 1 2注意第3元素左边2个元素,右边2个元素,因此下次折半的个数是2+1=3)
第八次折半:3(1 1 1注意第2元素左边1个元素,右边1个元素,因此下次折半的个数是1+1=2)
第九次折半:2
第十次折半:1
最多十次
答案选B。
第九题:
解析:
第一步:计算散列函数,将关键字填上去:
最后是这个样子:
第二步:计算查找失败的平均查找长度,做这个题需要我们非常的细心。首先,我们要清楚逻辑删除的概念:当我们删除掉散列表中的一个数之后,这个位置并不是为空了,里面的值会变为-1,为什么会这样的呢,因为假设如果表中还存在一个关键字0,
,我们算出来和25的位置是冲突的,经过线性探测再散列法之后串到了0的位置,如果我们使用线性查找到4这个位置的值时,发现为空的话,就不会继续查找了,就会漏点这个0,因为0原本也是在4这个位置的,所以这里的位置不是空,而是-1,我们在查找H=4时,查到里面的关键字是-1,说明还没有完事,接着向后查找到0这个位置,发现是空的,这时候才算是查找失败,因此查找H=4时,是要查找两次的,这个要注意。
查找失败的平均查找长度:是从这个点开始到下一个空节点的长度÷所有结点的个数之和。
这题要注意的就是查找H=4,失败的次数是2次。
答案选C。
第十题:
解析:
这个题太简单了,我们正常的话都会记住稳定的算法:冒泡排序,归并排序,直接插入,基数排序,计数排序,排除掉这些就是不稳定的算法,直接排除A,B,D
答案选C。
第十一题:
解析:考察快速排序的演变过程。
每一次排序之后,都会确定枢轴元素在序列中最终的位置,且它的左边都是小于这个枢轴元素的,右边都是大于这个枢轴元素的。显然这个枢轴元素就是81.
答案选D。
相关文章:

23年408数据结构
第一题: 解析: 第一点,我们要知道顺序存储的特点:优点就是随用随取,就是你想要查询第几个元素可以直接查询出来,时间复杂度就是O(1),缺点就是不适合删除和插入,因为每次删除和插入一…...

vue3ElementPlu表格合并多行
// 单元格合并逻辑 const objectSpanMethod ({ row, rowIndex, columnIndex }) > { const previousMachineModelUniqueId rowIndex > 0 ? tableData.value[rowIndex - 1].machineModel : null; const currentMachineModelUniqueId row.machineModel; // 合并“机型”…...

MySQL数据库 - 索引(上)
目录 1 简介 1.1 索引是什么 1.2 为什么要使用索引 2 索引应该选择哪种数据结构 2.1 HASH 2.2 二叉搜索树 2.3 N叉树(B树) 2.4 B树 3 MySQL的页 3.1 为什么要使用页 3.2 页文件头和页文件尾 3.3 页主体 3.4 页目录 4 B树在MySQL索引中的应…...
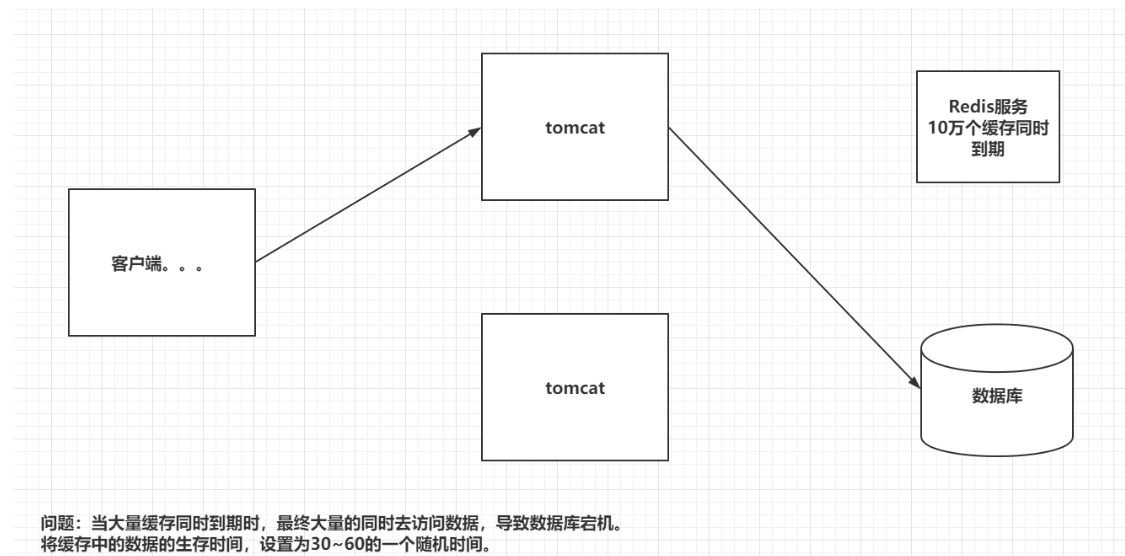
redis与springBoot整合
前提 要实现,使用Redis存储登录状态 需要一个完整的前端后端的项目 前端项目搭建 解压脚手架 安装依赖 配置请求代理 选做: 禁用EsLint语法检查 Vue Admin Template关闭eslint校验,lintOnSave:false设置无效解决办法_lintonsave: false-CSDN博客 …...

YoloV9改进策略:BackBone改进|CAFormer在YoloV9中的创新应用,显著提升目标检测性能
摘要 在目标检测领域,模型性能的提升一直是研究者和开发者们关注的重点。近期,我们尝试将CAFormer模块引入YoloV9模型中,以替换其原有的主干网络,这一创新性的改进带来了显著的性能提升。 CAFormer,作为MetaFormer框架下的一个变体,结合了深度可分离卷积和普通自注意力…...

消防应急物资仓库管理系统
集驰电子消防装备仓库管理系统(DW-S302系统)是一套成熟系统,依托3D技术、大数据、RFID技术、数据库技术、对装备器材进行统一管理,以RFID射频识别技术为核心,构建以物资综合管理为基础,智能分析定位为主要特色功能的装备器材库综合…...

【论文阅读】Semi-Supervised Few-shot Learning via Multi-Factor Clustering
通过多因素聚类的半监督小样本学习 引用:Ling J, Liao L, Yang M, et al. Semi-supervised few-shot learning via multi-factor clustering[C]//Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. 2022: 14564-14573. 论文地址…...

第十三章 RabbitMQ之消息幂等性
目录 一、引言 二、消息幂等解决方案 2.1. 方案一 2.2. 方案二 一、引言 幂等是一个数学概念,用函数表达式来描述是这样的:f(x) f(f(x)) 。在程序开发中,则是指同一个业务,执行一次或多次对业务状态的影响是一致的。有些业务…...
tpcms-master.zip
网盘:https://pan.notestore.cn/s.html?id34https://pan.notestore.cn/s.html?id34...

Spring国际化和Validation
SpringBoot国际化和Validation融合 场景 在应用交互时,可能需要根据客户端得语言来返回不同的语言数据。前端通过参数、请求头等往后端传入locale相关得参数,后端获取参数,根据不同得locale来获取不同得语言得文本信息返回给前端。 实现原…...
②EtherCAT转ModbusTCP, EtherCAT/Ethernet/IP/Profinet/ModbusTCP协议互转工业串口网关
EtherCAT/Ethernet/IP/Profinet/ModbusTCP协议互转工业串口网关https://item.taobao.com/item.htm?ftt&id822721028899 协议转换通信网关 EtherCAT 转 Modbus TCP (接上一章) GW系列型号 配置说明 上载 网线连接电脑到模块上的 WEB 网页设置网口&#…...

【华为HCIP实战课程八】OSPF网络类型及报文类型详解,网络工程师
一、点到点网络类型 1、两台路由器 2、支持广播、组播 P2P(PPP、HDLC、帧中继子接口) 我们需要三个维度考虑 A、是否自动通过组播发现邻居 B、时间(Hello和Dead) C、DR和BDR----多点接入网络需要用到(广播和NBMA) 点到点是组播自动发现邻居,Hello 10S,Dead 40S…...

信息安全工程师(28)机房安全分析与防护
前言 机房安全分析与防护是一个复杂而细致的过程,涉及到物理安全、环境控制、电力供应、数据安全、设备管理、人员管理以及紧急预案等多个方面。 一、机房安全分析 1. 物理安全威胁 非法入侵:未经授权的人员可能通过门窗、通风口等进入机房,…...

大数据处理从零开始————9.MapReduce编程实践之信息过滤之学生成绩统计demo
1.项目目标 1.1 需求概述 现在我们要统计某学校学生的成绩信息,筛选出成绩在60分及以上的学生。 1.2 业务分析 如果我们想实现该需求,可以通过编写一个MapReduce程序,来处理包含学生信息的文本文件,每行包含【学生的姓名&#x…...

自动化测试 | 窗口截图
driver.get_screenshot_as_file 是 Selenium WebDriver 的一个方法,它允许你将当前浏览器窗口(或标签页)的截图保存为文件。这个方法对于自动化测试中的截图验证非常有用,因为它可以帮助你捕获测试执行过程中的页面状态。 以下是…...

初中数学网上考试系统的设计与实现(论文+源码)_kaic
初中数学网上考试系统的设计与实现 学生: 指导教师: 摘 要:科技在人类的历史长流中愈洗愈精,不仅包括人们日常的生活起居,甚至还包括了考试的变化。之前的考试需要大量的时间和精力,组织者还需要挑选并考查…...

关系运算(3)
关系代数 昨天讲完附加关系代数运算,今天讲扩展关系代数运算。 扩展代数运算 正如其名,这种运算定义了前面基本和附加都没有的运算。 去重运算 可以将关系R中跟查询条件相关但是形成了重复的元组去除,只保留查询结果(简洁&…...

tp6的系统是如何上架的
TP6(ThinkPHP6)的系统上架过程,通常指的是将基于ThinkPHP6框架开发的应用程序部署到生产环境,并使其可以通过互联网访问。以下是一个大致的上架流程,包括准备工作、部署步骤以及后续维护等方面: 一、准备工…...

Vue:开发小技巧
目录 1. Table表格偏移 1. Table表格偏移 通过设置自小的宽度进行控制 :min-width <el-table-column label"操作" align"center" class-name"small-padding fixed-width" fixed"right" min-width"150px"><templa…...

力扣之1369.获取最近第二次的活动
题目: sql建表语句 Create table If Not Exists UserActivity (username varchar(30), activity varchar(30), startDate date, endDate date); Truncate table UserActivity; insert into UserActivity (username, activity, startDate, endDate) values (Alic…...

oracle与MySQL数据库之间数据同步的技术要点
Oracle与MySQL数据库之间的数据同步是一个涉及多个技术要点的复杂任务。由于Oracle和MySQL的架构差异,它们的数据同步要求既要保持数据的准确性和一致性,又要处理好性能问题。以下是一些主要的技术要点: 数据结构差异 数据类型差异ÿ…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...

数学建模-滑翔伞伞翼面积的设计,运动状态计算和优化 !
我们考虑滑翔伞的伞翼面积设计问题以及运动状态描述。滑翔伞的性能主要取决于伞翼面积、气动特性以及飞行员的重量。我们的目标是建立数学模型来描述滑翔伞的运动状态,并优化伞翼面积的设计。 一、问题分析 滑翔伞在飞行过程中受到重力、升力和阻力的作用。升力和阻力与伞翼面…...

Pydantic + Function Calling的结合
1、Pydantic Pydantic 是一个 Python 库,用于数据验证和设置管理,通过 Python 类型注解强制执行数据类型。它广泛用于 API 开发(如 FastAPI)、配置管理和数据解析,核心功能包括: 数据验证:通过…...

Spring Boot + MyBatis 集成支付宝支付流程
Spring Boot MyBatis 集成支付宝支付流程 核心流程 商户系统生成订单调用支付宝创建预支付订单用户跳转支付宝完成支付支付宝异步通知支付结果商户处理支付结果更新订单状态支付宝同步跳转回商户页面 代码实现示例(电脑网站支付) 1. 添加依赖 <!…...

LangChain【6】之输出解析器:结构化LLM响应的关键工具
文章目录 一 LangChain输出解析器概述1.1 什么是输出解析器?1.2 主要功能与工作原理1.3 常用解析器类型 二 主要输出解析器类型2.1 Pydantic/Json输出解析器2.2 结构化输出解析器2.3 列表解析器2.4 日期解析器2.5 Json输出解析器2.6 xml输出解析器 三 高级使用技巧3…...
)
背包问题双雄:01 背包与完全背包详解(Java 实现)
一、背包问题概述 背包问题是动态规划领域的经典问题,其核心在于如何在有限容量的背包中选择物品,使得总价值最大化。根据物品选择规则的不同,主要分为两类: 01 背包:每件物品最多选 1 次(选或不选&#…...

深入解析 ReentrantLock:原理、公平锁与非公平锁的较量
ReentrantLock 是 Java 中 java.util.concurrent.locks 包下的一个重要类,用于实现线程同步,支持可重入性,并且可以选择公平锁或非公平锁的实现方式。下面将详细介绍 ReentrantLock 的实现原理以及公平锁和非公平锁的区别。 ReentrantLock 实现原理 基本架构 ReentrantLo…...




















