10.11Python数学基础-多维随机变量及其分布
多维随机变量及其分布
1.二维随机变量及其分布
假设E是随机试验,Ω是样本空间,X、Y是Ω的两个变量;(X,Y)就叫做二维随机变量或二维随机向量。X、Y来自同一个样本空间。
联合分布函数
F ( x , y ) = P ( X ≤ x , Y ≤ y ) F(x,y)=P(X≤x,Y≤y) F(x,y)=P(X≤x,Y≤y)
几何意义表示对立体曲线的体积

用平面图形近似表示为:

即F(x,y)表示求(x,y)左下方的面积。
性质:
(1)0≤F(x,y) ≤1
(2)F(x,y) 不减,例如:y固定,x1<x2,F(x1,y)<F(x2,y)
(3)F(-∞,y)=F(x,-∞)=F(-∞,-∞)=0,F(+∞,+∞)=1
(4)F(x,y)分别关于x和y右连续
(5)
对于 x 1 < x 2 , y 1 < y 2 P ( x 1 < X ≤ x 2 , y 1 < Y ≤ y 2 ) = F ( x 2 , y 2 ) − F ( x 2 , y 1 ) − F ( x 1 , y 2 ) + F ( x 1 , y 1 ) 对于x_1<x_2,y_1<y_2\\ P(x_1<X≤x_2,y_1<Y≤y_2) = F(x_2,y_2) - F(x_2,y_1)-F(x_1,y_2)+F(x_1,y_1) 对于x1<x2,y1<y2P(x1<X≤x2,y1<Y≤y2)=F(x2,y2)−F(x2,y1)−F(x1,y2)+F(x1,y1)
图形解释:
P ( x 1 < X ≤ x 2 , y 1 < Y ≤ y 2 ) P(x_1<X≤x_2,y_1<Y≤y_2) P(x1<X≤x2,y1<Y≤y2)
表示求以下图形的面积:

等式右边的分布函数用如下图形表示:

F ( x 2 , y 2 ) F(x_2,y_2) F(x2,y2)
表示图中蓝色区域
F ( x 2 , y 1 ) F(x_2,y_1) F(x2,y1)
表示红色区域
F ( x 1 , y 2 ) F(x_1,y_2) F(x1,y2)
表示黄色色区域
所以
F ( x 2 , y 2 ) − F ( x 2 , y 1 ) − F ( x 1 , y 2 ) F(x_2,y_2) - F(x_2,y_1)-F(x_1,y_2) F(x2,y2)−F(x2,y1)−F(x1,y2)
就是只有蓝色的区域
但是
F ( x 1 , y 1 ) F(x_1,y_1) F(x1,y1)
的区域在减的过程中被减掉了两次,需要补回来一次,所以:
F ( x 2 , y 2 ) − F ( x 2 , y 1 ) − F ( x 1 , y 2 ) + F ( x 1 , y 1 ) F(x_2,y_2) - F(x_2,y_1)-F(x_1,y_2)+F(x_1,y_1) F(x2,y2)−F(x2,y1)−F(x1,y2)+F(x1,y1)
所表示的图形面积才是
P ( x 1 < X ≤ x 2 , y 1 < Y ≤ y 2 ) P(x_1<X≤x_2,y_1<Y≤y_2) P(x1<X≤x2,y1<Y≤y2)
所以:
对于 x 1 < x 2 , y 1 < y 2 P ( x 1 < X ≤ x 2 , y 1 < Y ≤ y 2 ) = F ( x 2 , y 2 ) − F ( x 2 , y 1 ) − F ( x 1 , y 2 ) + F ( x 1 , y 1 ) 对于x_1<x_2,y_1<y_2\\ P(x_1<X≤x_2,y_1<Y≤y_2) = F(x_2,y_2) - F(x_2,y_1)-F(x_1,y_2)+F(x_1,y_1) 对于x1<x2,y1<y2P(x1<X≤x2,y1<Y≤y2)=F(x2,y2)−F(x2,y1)−F(x1,y2)+F(x1,y1)
边缘分布
X的边缘分布:
F X ( x ) = P ( X ≤ x ) = F ( x , + ∞ ) = P ( X ≤ x , Y < + ∞ ) F_X(x) = P(X≤x) = F(x,+∞) = P(X≤x,Y<+∞) FX(x)=P(X≤x)=F(x,+∞)=P(X≤x,Y<+∞)
这表示在所有可能的 Y 值上,X 取值 x 的概率总和。从图形曲线上理解就是求小于x的所有点的面积,Y随意取值。
Y的边缘分布:
F Y ( y ) = P ( Y ≤ y ) = F ( + ∞ , y ) = P ( X < + ∞ , Y ≤ y ) F_Y(y) = P(Y≤y) = F(+∞,y) = P(X<+∞,Y≤y) FY(y)=P(Y≤y)=F(+∞,y)=P(X<+∞,Y≤y)
表示在所有可能的 X 值上,Y 取值 y的概率总和。从图形曲线上理解就是求小于y的所有点的面积,X随意取值。
2.二维离散型随机变量的联合分布和边缘分布
联合概率质量函数 P(X=x,Y=y) 描述了随机变量 X 和 Y 同时取特定值 x 和y 的概率。联合PMF满足以下性质:
-
非负性:对于所有的 x 和 y,有 P(X=x,Y=y)≥0。
-
归一性:所有可能的 x 和 y 值的概率之和等于1,即:
∑ x ∑ y P ( X = x , Y = y ) = 1 ∑_x∑_yP(X=x,Y=y)=1 x∑y∑P(X=x,Y=y)=1
概率分布表解释:
假设由一个概率分布表:
| X\Y | 1 | 2 | 3 |
|---|---|---|---|
| 1 | 0 | 1/2 | 1/8 |
| 2 | 1/8 | 1/8 | 1/8 |
非负性表示分布表中的所有概率都要大于等于0。例如:
P ( X = 1 , Y = 2 ) = 1 2 ≥ 0 P ( X = 2 , Y = 2 ) = 1 8 ≥ 0 P(X=1,Y=2)=\dfrac{1}{2}\geq 0\\ P(X=2,Y=2)=\dfrac{1}{8}\geq 0 P(X=1,Y=2)=21≥0P(X=2,Y=2)=81≥0
归一性表示分布表中所有概率之和等于1。
联合分布函数
F ( x , y ) = P ( X ≤ x , Y ≤ y ) = ∑ x i ≤ x ∑ y j ≤ y P ( X = x , Y = y ) F(x,y)=P(X\leq x,Y\leq y)=∑_{x_i\leq x}∑_{y_j\leq y}P(X=x,Y=y) F(x,y)=P(X≤x,Y≤y)=xi≤x∑yj≤y∑P(X=x,Y=y)
概率分布表解释:
F(x,y)的值就是在分布表中找到对应的(x,y)对应的位置,然后将其左上角的概率相加。
例如:
F ( 1 , 2 ) = P ( X ≤ 1 , Y ≤ 2 ) = P ( 1 , 1 ) + P ( 1 , 2 ) = 0 + 1 2 = 1 2 F ( 2 , 2 ) = P ( X ≤ 2 , Y ≤ 2 ) = P ( 1 , 1 ) + P ( 1 , 2 ) + P ( 2 , 1 ) + P ( 2 , 2 ) = 0 + 1 2 + 1 8 + 1 8 = 3 4 F(1,2)=P(X\leq 1,Y\leq 2)=P(1,1)+P(1,2)=0+\dfrac{1}{2}=\dfrac{1}{2}\\ F(2,2)=P(X\leq 2,Y\leq 2)=P(1,1)+P(1,2)+P(2,1)+P(2,2)=0+\dfrac{1}{2}+\dfrac{1}{8}+\dfrac{1}{8}=\dfrac{3}{4} F(1,2)=P(X≤1,Y≤2)=P(1,1)+P(1,2)=0+21=21F(2,2)=P(X≤2,Y≤2)=P(1,1)+P(1,2)+P(2,1)+P(2,2)=0+21+81+81=43
边缘分布
边缘概率质量函数可以通过对联合PMF的适当求和得到。
-
边缘PMF
P X ( x ) P_X(x) PX(x)
:表示随机变量 X 取特定值 x 的概率,不考虑 Y的值。计算方法为:
P X ( x ) = ∑ y P ( X = x , Y = y ) P_X(x)=∑_yP(X=x,Y=y) PX(x)=y∑P(X=x,Y=y)
其中,求和是对所有可能的 y 值进行。 -
边缘PMF
P Y ( y ) P_Y(y) PY(y)
:表示随机变量 Y取特定值 y 的概率,不考虑 X 的值。计算方法为:
P Y ( y ) = ∑ x P ( X = x , Y = y ) P_Y(y)=∑_xP(X=x,Y=y) PY(y)=x∑P(X=x,Y=y)
其中,求和是对所有可能的 x 值进行。
概率分布表解释:
对行求和,得到对X的边缘分布。
对列求和,得到对Y的边缘分布。
例如:
| X\Y | 1 | 2 | 3 |
|---|---|---|---|
| 1 | 0 | 1/2 | 1/8 |
| 2 | 1/8 | 1/8 | 1/8 |
求X的边缘分布:
| X | 1 | 2 |
|---|---|---|
| P | 5/8 | 3/8 |
当X=1时,求该行的概率之和,即:0+1/2+1/8=5/8
以此类推。
求Y的边缘分布:
| Y | 1 | 2 | 3 |
|---|---|---|---|
| P | 1/8 | 5/8 | 1/4 |
当Y=1时,求该列的概率之和,即0+1/8=1/8
以此类推。
3.二维连续随机变量的联合密度和边缘密度函数
对于二维连续随机变量 X 和 Y,其分布函数为:
F ( x , y ) = P ( X ≤ x , Y ≤ y ) = ∫ − ∞ x ∫ − ∞ y f ( s , t ) d s d t F(x,y) = P(X≤x,Y≤y) = ∫_{-∞}^x∫_{-∞}^yf(s,t)dsdt F(x,y)=P(X≤x,Y≤y)=∫−∞x∫−∞yf(s,t)dsdt
则F(x,y)是分布函数,f(x,y)是联合密度函数。
f(x,y)的性质:
-
非负性:对于所有的 x 和 y,有 f(x,y)≥0。
-
归一性:在整个 x 和 y 的取值范围上的积分等于1,即:
∫ − ∞ + ∞ ∫ − ∞ + ∞ f ( x , y ) d x d y = 1 ∫_{-\infty}^{+\infty}∫_{-\infty}^{+\infty}f(x,y) dxdy=1 ∫−∞+∞∫−∞+∞f(x,y) dxdy=1
这个积分是对所有可能的 x 和 y 值进行的。
例子
假设联合密度函数:
f ( x , y ) = { e − ( x + y ) , x > 0 , y > 0 0 , 其它 f(x,y)=\begin{cases} e^{-(x+y)}, & x>0,y>0\\ 0,& 其它 \end{cases} f(x,y)={e−(x+y),0,x>0,y>0其它
求分布函数F(x,y)
解:
根据分布函数可知:
F ( x , y ) = P ( X ≤ x , Y ≤ y ) = ∫ − ∞ x ∫ − ∞ y f ( s , t ) d s d t F(x,y) = P(X≤x,Y≤y) = ∫_{-∞}^x∫_{-∞}^yf(s,t)dsdt F(x,y)=P(X≤x,Y≤y)=∫−∞x∫−∞yf(s,t)dsdt
当x>0且y>0时
∫ − ∞ x ∫ − ∞ y f ( s , t ) d s d t = ∫ 0 x ∫ 0 y e − ( s + t ) d s d t = ∫ 0 x e − s d s ∫ 0 y e − t d t = ( 1 − e − x ) ( 1 − e − y ) ∫_{-∞}^x∫_{-∞}^yf(s,t)dsdt=∫_{0}^x∫_{0}^ye^{-(s+t)}dsdt=∫_{0}^xe^{-s}ds∫_{0}^ye^{-t}dt=(1-e^{-x})(1-e^{-y}) ∫−∞x∫−∞yf(s,t)dsdt=∫0x∫0ye−(s+t)dsdt=∫0xe−sds∫0ye−tdt=(1−e−x)(1−e−y)
当x,y有一个小于0时
F ( x , y ) = P ( X ≤ x , Y ≤ y ) = ∫ − ∞ x ∫ − ∞ y f ( s , t ) d s d t = 0 F(x,y) = P(X≤x,Y≤y) = ∫_{-∞}^x∫_{-∞}^yf(s,t)dsdt=0 F(x,y)=P(X≤x,Y≤y)=∫−∞x∫−∞yf(s,t)dsdt=0
所以
F ( x , y ) = { ( 1 − e − x ) ( 1 − e − y ) , x > 0 , y > 0 0 , 其它 F(x,y)=\begin{cases} (1-e^{-x})(1-e^{-y}), & x>0,y>0\\ 0,& 其它 \end{cases} F(x,y)={(1−e−x)(1−e−y),0,x>0,y>0其它
边缘密度函数
边缘分布函数:
F X ( x ) = F ( x , + ∞ ) = ∫ − ∞ x [ ∫ − ∞ + ∞ f ( s , t ) d t ] d s F_X(x)=F(x,+\infty)=\int _{-\infty}^x[\int _{-\infty}^{+\infty}f(s,t)dt]ds FX(x)=F(x,+∞)=∫−∞x[∫−∞+∞f(s,t)dt]ds
求导,得出边缘密度函数:
f X ( x ) = ∫ − ∞ + ∞ f ( x , t ) d t = ∫ − ∞ + ∞ f ( x , y ) d y f Y ( y ) = ∫ − ∞ + ∞ f ( s , y ) d s = ∫ − ∞ + ∞ f ( x , y ) d x f_X(x)=\int _{-\infty}^{+\infty}f(x,t)dt=\int _{-\infty}^{+\infty}f(x,y)dy\\ f_Y(y)=\int _{-\infty}^{+\infty}f(s,y)ds=\int _{-\infty}^{+\infty}f(x,y)dx fX(x)=∫−∞+∞f(x,t)dt=∫−∞+∞f(x,y)dyfY(y)=∫−∞+∞f(s,y)ds=∫−∞+∞f(x,y)dx
求X的边缘密度函数就是对y求积分,对Y的边缘密度函数就是对x求积分。
例子
假设联合密度函数:
f ( x , y ) = 1 π 2 ( 1 + x 2 ) ( 1 + y 2 ) f(x,y)=\dfrac{1}{\pi^2(1+x^2)(1+y^2)} f(x,y)=π2(1+x2)(1+y2)1
求边缘密度函数。
解:
对X的边缘密度函数:
f X ( x ) = ∫ − ∞ + ∞ f ( x , y ) d y = ∫ − ∞ + ∞ 1 π 2 ( 1 + x 2 ) ( 1 + y 2 ) d y = 1 π 2 ( 1 + x 2 ) ∫ − ∞ + ∞ 1 ( 1 + y 2 ) d y = 1 π 2 ( 1 + x 2 ) ∫ − ∞ + ∞ a r c t a n ( y ) ∣ − ∞ + ∞ = 1 π ( 1 + x 2 ) f_X(x)=\int _{-\infty}^{+\infty}f(x,y)dy=\int _{-\infty}^{+\infty}\dfrac{1}{\pi^2(1+x^2)(1+y^2)}dy\\ =\dfrac{1}{\pi^2(1+x^2)}\int _{-\infty}^{+\infty}\dfrac{1}{(1+y^2)}dy=\dfrac{1}{\pi^2(1+x^2)}\int _{-\infty}^{+\infty}arctan(y)|_{-\infty}^{+\infty}=\dfrac{1}{\pi(1+x^2)} fX(x)=∫−∞+∞f(x,y)dy=∫−∞+∞π2(1+x2)(1+y2)1dy=π2(1+x2)1∫−∞+∞(1+y2)1dy=π2(1+x2)1∫−∞+∞arctan(y)∣−∞+∞=π(1+x2)1
对Y的边缘密度函数:
f Y ( y ) = ∫ − ∞ + ∞ f ( x , y ) d y = 1 π ( 1 + y 2 ) f_Y(y)=\int _{-\infty}^{+\infty}f(x,y)dy=\dfrac{1}{\pi(1+y^2)} fY(y)=∫−∞+∞f(x,y)dy=π(1+y2)1
4.条件分布
条件分布是指在已知另一个随机变量或事件的条件下,该随机变量的概率分布。
F ( x ∣ A ) = P ( X ≤ x ∣ A ) F(x|A)=P(X\leq x | A) F(x∣A)=P(X≤x∣A)
例子
假设概率密度函数
f ( x ) = 1 π ( 1 + x 2 ) f(x)=\dfrac{1}{\pi(1+x^2)} f(x)=π(1+x2)1
求在X>1的条件下f(x)的条件分布函数
解:
F ( x ∣ X > 1 ) = P ( X ≤ x ∣ X > 1 ) F(x|X>1)=P(X\leq x|X>1) F(x∣X>1)=P(X≤x∣X>1)
当x≤1时:
不满足条件
F ( x ∣ X > 1 ) = 0 F(x|X>1)=0 F(x∣X>1)=0
当x>1时:
F ( x ∣ X > 1 ) = P ( X ≤ x ∣ X > 1 ) = P ( X ≤ x , X > 1 ) P ( X > 1 ) F(x|X>1)=P(X\leq x|X>1)=\dfrac{P(X\leq x,X>1)}{P(X>1)} F(x∣X>1)=P(X≤x∣X>1)=P(X>1)P(X≤x,X>1)
计算分子:
P ( X ≤ x , X > 1 ) = P ( 1 ≤ X ≤ x ) = ∫ 1 x 1 π ( 1 + x 2 ) d x = 1 π a r c t a n ( x ) ∣ 1 x = a r c t a n x π − 1 π . π 4 = a r c t a n x π − 1 4 P(X\leq x,X>1)=P(1\leq X\leq x)=\int _1^x\dfrac{1}{\pi(1+x^2)}dx=\dfrac{1}{\pi}arctan(x)|_1^x=\dfrac{arctanx}{\pi}-\dfrac{1}{\pi}.\dfrac{\pi}{4}=\dfrac{arctanx}{\pi}-\dfrac{1}{4} P(X≤x,X>1)=P(1≤X≤x)=∫1xπ(1+x2)1dx=π1arctan(x)∣1x=πarctanx−π1.4π=πarctanx−41
计算分母:
P ( X > 1 ) = ∫ 1 + ∞ 1 π ( 1 + x 2 ) d x = 1 π a r c t a n ( x ) ∣ 1 + ∞ = 1 π . ( π 2 − π 4 ) = 1 4 P(X>1)=\int _1^{+\infty}\dfrac{1}{\pi(1+x^2)}dx=\dfrac{1}{\pi}arctan(x)|_1^{+\infty}=\dfrac{1}{\pi}.(\dfrac{\pi}{2}-\dfrac{\pi}{4})=\dfrac{1}{4} P(X>1)=∫1+∞π(1+x2)1dx=π1arctan(x)∣1+∞=π1.(2π−4π)=41
则
F ( x ∣ X > 1 ) = P ( X ≤ x , X > 1 ) P ( X > 1 ) = 4 a r c t a n x π − 1 F(x|X>1)=\dfrac{P(X\leq x,X>1)}{P(X>1)}=\dfrac{4arctanx}{\pi}-1 F(x∣X>1)=P(X>1)P(X≤x,X>1)=π4arctanx−1
所以在X>1的条件下f(x)的条件分布函数
F ( x ∣ X > 1 ) = { 4 a r c t a n x π − 1 , x > 1 0 , x ≤ 1 F(x|X>1)=\begin{cases} \dfrac{4arctanx}{\pi}-1, & x>1\\ 0,& x≤1 \end{cases} F(x∣X>1)=⎩ ⎨ ⎧π4arctanx−1,0,x>1x≤1
5.离散型随机变量的条件分布
条件概率质量函数定义为:
P ( X = x ∣ Y = y ) = P ( X = x , Y = y ) P ( Y = y ) P(X=x∣Y=y)=\dfrac{P(X=x,Y=y)}{P(Y=y)} P(X=x∣Y=y)=P(Y=y)P(X=x,Y=y)
其中 P(X=x,Y=y)是 X 和 Y的联合概率质量函数,P(Y=y) 是 Y 的边缘概率质量函数。
从分布表来理解:
假设概率分布表:
| X\Y | 0 | 1 |
|---|---|---|
| 0 | 0.1 | 0.3 |
| 1 | 0.3 | 0.3 |
P(Y=y) 是 Y 的边缘概率质量函数,Y 的边缘概率质量函数是对列求和:
| Y | 0 | 1 |
|---|---|---|
| P | 0.4 | 0.6 |
那么在Y=1的条件下,假设x=0,X=x的概率为:
P ( X = 0 ∣ Y = 1 ) = P ( X = 0 , Y = 1 ) P ( Y = 1 ) = 0.3 0.6 = 0.5 P(X=0∣Y=1)=\dfrac{P(X=0,Y=1)}{P(Y=1)}=\dfrac{0.3}{0.6}=0.5 P(X=0∣Y=1)=P(Y=1)P(X=0,Y=1)=0.60.3=0.5
假设x=1,X=x的概率为:
P ( X = 1 ∣ Y = 1 ) = P ( X = 1 , Y = 1 ) P ( Y = 1 ) = 0.3 0.6 = 0.5 P(X=1∣Y=1)=\dfrac{P(X=1,Y=1)}{P(Y=1)}=\dfrac{0.3}{0.6}=0.5 P(X=1∣Y=1)=P(Y=1)P(X=1,Y=1)=0.60.3=0.5
则在Y=1的条件下,X的分布函数为:
| X | 0 | 1 |
|---|---|---|
| P(X|Y=1) | 0.3 | 0.3 |
其它情况如Y=0条件下X的分布函数、X=0及X=1条件下Y的分布函数同上。
6.连续型随机变量的条件分布
在Y=y条件下,条件概率密度函数为:
f ( x ∣ y ) = f ( x , y ) f Y ( y ) f(x∣y)=\dfrac{f(x,y)}{f_Y(y)} f(x∣y)=fY(y)f(x,y)
其中 f(x,y) 是 X 和 Y 的联合概率密度函数,
f Y ( y ) f_Y(y) fY(y)
是 Y的边缘概率密度函数。
同理,在X=x条件下,条件概率密度函数为:
f ( y ∣ x ) = f ( x , y ) f X ( x ) f(y∣x)=\dfrac{f(x,y)}{f_X(x)} f(y∣x)=fX(x)f(x,y)
其中 f(x,y) 是 X 和 Y 的联合概率密度函数,
f X ( x ) f_X(x) fX(x)
是 X的边缘概率密度函数。
在Y=y的条件下,X的条件分布函数:
F ( x ∣ y ) = ∫ − ∞ x f ( x ∣ y ) d x = ∫ − ∞ x f ( u , y ) f Y ( y ) d u F(x|y)=\int _{-\infty}^xf(x∣y)dx=\int _{-\infty}^x\dfrac{f(u,y)}{f_Y(y)}du F(x∣y)=∫−∞xf(x∣y)dx=∫−∞xfY(y)f(u,y)du
在X=x的条件下,Y的条件分布函数:
F ( y ∣ x ) = ∫ − ∞ y f ( y ∣ x ) d y = ∫ − ∞ y f ( x , v ) f X ( x ) d v F(y|x)=\int _{-\infty}^yf(y∣x)dy=\int _{-\infty}^y\dfrac{f(x,v)}{f_X(x)}dv F(y∣x)=∫−∞yf(y∣x)dy=∫−∞yfX(x)f(x,v)dv
例子
假设
f ( x , y ) = 1 π 2 ( 1 + x 2 ) ( 1 + y 2 ) , f X ( x ) = 1 π ( 1 + x 2 ) , f Y ( y ) = 1 π ( 1 + y 2 ) f(x,y)=\dfrac{1}{\pi^2(1+x^2)(1+y^2)},f_X(x)=\dfrac{1}{\pi(1+x^2)},f_Y(y)=\dfrac{1}{\pi(1+y^2)} f(x,y)=π2(1+x2)(1+y2)1,fX(x)=π(1+x2)1,fY(y)=π(1+y2)1
求
在Y=y的条件下,X的条件密度函数;在X=x的条件下,Y的条件密度函数。
解:
f ( x ∣ y ) = f ( x , y ) f Y ( y ) = π ( 1 + y 2 ) π 2 ( 1 + x 2 ) ( 1 + y 2 ) = 1 π ( 1 + x 2 ) f ( y ∣ x ) = f ( x , y ) f X ( x ) = π ( 1 + x 2 ) π 2 ( 1 + x 2 ) ( 1 + y 2 ) = 1 π ( 1 + y 2 ) f(x|y)=\dfrac{f(x,y)}{f_Y(y)}=\dfrac{\pi(1+y^2)}{\pi^2(1+x^2)(1+y^2)}=\dfrac{1}{\pi(1+x^2)}\\ f(y|x)=\dfrac{f(x,y)}{f_X(x)}=\dfrac{\pi(1+x^2)}{\pi^2(1+x^2)(1+y^2)}=\dfrac{1}{\pi(1+y^2)} f(x∣y)=fY(y)f(x,y)=π2(1+x2)(1+y2)π(1+y2)=π(1+x2)1f(y∣x)=fX(x)f(x,y)=π2(1+x2)(1+y2)π(1+x2)=π(1+y2)1
7.随机变量的独立性
定义
两个随机变量 XX 和 YY 被称为独立的,如果它们满足以下条件:
对于连续型随机变量:它们的联合概率密度函数f(x,y)可以表示为各自边缘概率密度函数的乘积:
f ( x , y ) = f X ( x ) ⋅ f Y ( y ) f(x,y)=f_X(x)⋅f_Y(y) f(x,y)=fX(x)⋅fY(y)
对于离散型随机变量:它们的联合概率质量函数P(X=x,Y=y)可以表示为各自边缘概率质量函数的乘积:
P ( X = x , Y = y ) = P ( X = x ) ⋅ P ( Y = y ) P(X=x,Y=y)=P(X=x)⋅P(Y=y) P(X=x,Y=y)=P(X=x)⋅P(Y=y)
例子
1.假设我们有两个公平的六面骰子,我们分别将它们记为骰子A和骰子B。
随机变量定义为:
让 X 表示骰子A的结果。
让 Y 表示骰子B的结果。
事件:
事件 A:“骰子A显示的数字大于3”。
事件 B:“骰子B显示的数字是偶数”。
问事件A和B是否独立。
解:
联合概率分布表:
| X\Y | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| 1 | 1\36 | 1\36 | 1\36 | 1\36 | 1\36 | 1\36 |
| 2 | 1\36 | 1\36 | 1\36 | 1\36 | 1\36 | 1\36 |
| 3 | 1\36 | 1\36 | 1\36 | 1\36 | 1\36 | 1\36 |
| 4 | 1\36 | 1\36 | 1\36 | 1\36 | 1\36 | 1\36 |
| 5 | 1\36 | 1\36 | 1\36 | 1\36 | 1\36 | 1\36 |
| 6 | 1\36 | 1\36 | 1\36 | 1\36 | 1\36 | 1\36 |
X的边缘概率分布表:
| X | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| P | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 |
Y的边缘概率分布表:
| Y | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| P | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 |
事件A的概率:
P ( A ) = P ( X > 3 ) = P ( X = 4 ) + P ( X = 5 ) + P ( X = 6 ) = 1 / 2 P(A)=P(X>3)=P(X=4)+P(X=5)+P(X=6)=1/2 P(A)=P(X>3)=P(X=4)+P(X=5)+P(X=6)=1/2
事件B的概率:
P ( B ) = P ( Y = 2 ) + P ( Y = 4 ) + P ( Y = 6 ) = 1 / 2 P(B)=P(Y=2)+P(Y=4)+P(Y=6)=1/2 P(B)=P(Y=2)+P(Y=4)+P(Y=6)=1/2
事件A和B的联合概率:
P ( A B ) = P ( X = 4 , Y = 2 ) + P ( X = 4 , Y = 4 ) + P ( X = 4 , Y = 6 ) + P ( X = 5 , Y = 2 ) + P ( X = 5 , Y = 4 ) + P ( X = 5 , Y = 6 ) + P ( X = 6 , Y = 2 ) + P ( X = 6 , Y = 4 ) + P ( X = 6 , Y = 6 ) = 1 / 4 P(AB)=P(X=4,Y=2)+P(X=4,Y=4)+P(X=4,Y=6)\\ +P(X=5,Y=2)+P(X=5,Y=4)+P(X=5,Y=6)\\ +P(X=6,Y=2)+P(X=6,Y=4)+P(X=6,Y=6)=1/4 P(AB)=P(X=4,Y=2)+P(X=4,Y=4)+P(X=4,Y=6)+P(X=5,Y=2)+P(X=5,Y=4)+P(X=5,Y=6)+P(X=6,Y=2)+P(X=6,Y=4)+P(X=6,Y=6)=1/4
所以
P ( A B ) = P ( A ) P ( B ) = 1 / 4 P(AB)=P(A)P(B)=1/4 P(AB)=P(A)P(B)=1/4
所以A、B事件是独立的。
2.假设经理8-12点到公司,秘书7-9点到公司,经理和秘书到公司的事件是独立的,求经理和秘书到公司的联合概率。
解:
设X是经理到公司的事件,Y为秘书到公司的事件,则:X、Y的密度函数服从均匀分布。
f ( x ) = { 1 4 , 8 < x < 12 0 , 其它 f(x)=\begin{cases} \dfrac{1}{4},& 8<x<12\\ 0, & 其它 \end{cases} f(x)=⎩ ⎨ ⎧41,0,8<x<12其它
f ( y ) = { 1 2 , 7 < y < 9 0 , 其它 f(y)=\begin{cases} \dfrac{1}{2},& 7<y<9\\ 0, & 其它 \end{cases} f(y)=⎩ ⎨ ⎧21,0,7<y<9其它
由于X、Y是独立的,则联合密度函数:
f ( x , y ) = f ( x ) f ( y ) = { 1 8 , 8 < x < 12 , 7 < y < 9 0 , 其它 f(x,y)=f(x)f(y)=\begin{cases} \dfrac{1}{8},& 8<x<12,7<y<9\\ 0, & 其它 \end{cases} f(x,y)=f(x)f(y)=⎩ ⎨ ⎧81,0,8<x<12,7<y<9其它
8.二维随机变量函数的分布
8.1 二维离散型随机变量函数的分布
二维离散型随机变量函数的分布指的是在给定两个离散型随机变量 X 和 Y的情况下,它们函数 Z=g(X,Y)的分布。这里
g(X,Y)是一个定义在 X和 Y取值范围内的函数。
要找到函数 Z 的分布,我们需要确定 Z 的每一个可能值的概率。具体步骤如下:
- 确定函数的输出值:列出函数 Z=g(X,Y)可能的所有输出值。
- 计算每个输出值的概率:对于每一个可能的输出值 z,计算 Z=z的概率。这通常涉及到对 X 和 Y的联合概率质量函数 P(X=x,Y=y)进行求和。
- 构建概率质量函数:构建函数 Z 的概率质量函数,即对于每一个可能的 z,确定 P(Z=z)。
例子
假设有两个离散型随机变量 XX 和 YY,它们的联合PMF如下表所示:
| X \ Y | 1 | 2 | 3 |
|---|---|---|---|
| 1 | 0.1 | 0.2 | 0.0 |
| 2 | 0.0 | 0.3 | 0.0 |
| 3 | 0.1 | 0.1 | 0.2 |
求函数 Z=X+Y。
解:
-
确定函数的输出值:列出所有可能的 X 和 Y组合的和。
1+1=2
1+2=3
1+3=4
2+2=4
2+3=5
3+3=6
所以,Z 可能的值是 2, 3, 4, 5, 6。
-
计算每个输出值的概率:
P(Z=2)=P(X=1,Y=1)=0.1
P(Z=3)=P(X=1,Y=2)+P(X=2,Y=1)=0.2
P(Z=4)=P(X=1,Y=3)+P(X=2,Y=2)+P(X=3,Y=1)=0.0+0.3+0.1=0.4
P(Z=5)=P(X=2,Y=3)+P(X=3,Y=2)=0.1
P(Z=6)=P(X=3,Y=3)=0.2
-
构建概率质量函数:
P(Z=2)=0.1
P(Z=3)=0.2
P(Z=4)=0.4
P(Z=5)=0.1
P(Z=6)=0.2
-
函数分布表为:
Z 2 3 4 5 6 P 0.1 0.2 0.4 0.1 0.2
以上的解法比较麻烦,可以根据分布表来计算。
1.根据Z=X+Y,将X的每行分别于Y的每列分别相加,得到Z的取值,再按X、Y在表格中对应的单元格中的值照抄过来,得到:
| Z | 2 | 3 | 4 | 3 | 4 | 5 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|---|---|
| P | 0.1 | 0.2 | 0.0 | 0.0 | 0.3 | 0.0 | 0.1 | 0.1 | 0.2 |
2.合并Z中重复的值及对应的概率,即概率相加:
| Z | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|
| P | 0.1 | 0.2 | 0.4 | 0.1 | 0.2 |
8.2 二维连续型随机变量函数的分布
二维连续型随机变量函数的分布是指由两个连续型随机变量 (X,Y)构成的联合分布,并通过某种函数关系 Z=g(X,Y)得到一个新的随机变量 Z
的分布。
假设 (X,Y)是一个二维连续型随机变量,其联合概率密度函数为 f(x,y)。设 Z=g(X,Y) 是一个函数关系,其中 g 是一个已知的函数。我们需要
找到 Z 的概率密度函数
f Z ( z ) f_Z(z) fZ(z)
具体步骤如下:
-
计算 Z的累积分布函数
F Z ( z ) F_Z(z) FZ(z)
:
F Z ( z ) = P ( Z ≤ z ) = P ( g ( X , Y ) ≤ z ) F_Z(z)=P(Z≤z)=P(g(X,Y)≤z) FZ(z)=P(Z≤z)=P(g(X,Y)≤z)这可以通过对联合分布函数进行积分得到:
F Z ( z ) = ∬ g ( x , y ) ≤ z f ( x , y ) d x d y F_Z(z)=∬_{g(x,y)≤z}f(x,y) dx dy FZ(z)=∬g(x,y)≤zf(x,y) dx dy -
求导得到概率密度函数
f Z ( z ) f_Z(z) fZ(z)
:
f Z ( z ) = d d z F Z ( z ) f_Z(z)=\dfrac{d}{dz}F_Z(z) fZ(z)=dzdFZ(z)
对于某些特定的函数 g(X,Y),可以直接求出 Z 的概率密度函数。例如,如果 g(X,Y)=X+Y,则可以通过以下步骤求出 Z 的概率密度函数:
-
确定 Z 的范围:
Z=X+Y
确定 Z 的可能取值范围。 -
计算 Z的概率密度函数:
f Z ( z ) = ∫ − ∞ ∞ f X ( x ) f Y ( z − x ) d x f_Z(z)=∫_{−∞}^∞f_X(x)f_Y(z−x)dx fZ(z)=∫−∞∞fX(x)fY(z−x)dx这称为卷积公式。
例子
假设 (X,Y) 的联合概率密度函数为:
f ( x , y ) = { 2 , 0 ≤ x ≤ 1 , 0 ≤ y ≤ 1 0 , otherwise f(x, y) = \begin{cases} 2, & 0 \leq x \leq 1, 0 \leq y \leq 1 \\ 0, & \text{otherwise} \end{cases} f(x,y)={2,0,0≤x≤1,0≤y≤1otherwise
求Z*=*X+Y的分布
解:
确定Z的范围:
0 ≤ Z ≤ 2 0\leq Z \leq 2 0≤Z≤2
先求分布函数:
F Z ( z ) = P ( Z ≤ z ) = ∬ g ( x , y ) ≤ z f ( x , y ) d x d y F_Z(z)=P(Z≤z)=∬_{g(x,y)≤z}f(x,y) dx dy FZ(z)=P(Z≤z)=∬g(x,y)≤zf(x,y) dx dy
当z<0时,因为x、y都大于0,所以事件不可能发生
F Z ( z ) = 0 F_Z(z)=0 FZ(z)=0
当0≤z≤1时,画出图形:

根据图形可知
0 ≤ x ≤ z , 0 ≤ y ≤ z − x 0≤x≤z,0≤y≤z-x 0≤x≤z,0≤y≤z−x
F Z ( z ) = P ( Z ≤ z ) = ∬ g ( x , y ) ≤ z f ( x , y ) d x d y = ∫ 0 z d x ∫ 0 z − x 2 d y = 2 ∫ 0 z ( z − x ) d x = 2 ( z x − 1 2 x 2 ) ∣ 0 z = z 2 F_Z(z)=P(Z≤z)=∬_{g(x,y)≤z}f(x,y) dx dy=\int_0^zdx\int_0^{z-x}2dy=2\int_0^z(z-x)dx=2(zx-\dfrac{1}{2}x^2)|_0^z=z^2 FZ(z)=P(Z≤z)=∬g(x,y)≤zf(x,y) dx dy=∫0zdx∫0z−x2dy=2∫0z(z−x)dx=2(zx−21x2)∣0z=z2
当1≤z≤2时,画出图形:

根据图形可知:
所求面积=1-右上角三角形面积S
S = ( 2 − z ) 2 2 S=\dfrac{(2-z)^2}{2} S=2(2−z)2
F Z ( z ) = P ( Z ≤ z ) = ∬ g ( x , y ) ≤ z f ( x , y ) d x d y = 2 ( 1 − ( 2 − z ) 2 2 ) = 2 − ( 2 − z ) 2 F_Z(z)=P(Z≤z)=∬_{g(x,y)≤z}f(x,y) dx dy=2(1-\dfrac{(2-z)^2}{2})=2-(2-z)^2 FZ(z)=P(Z≤z)=∬g(x,y)≤zf(x,y) dx dy=2(1−2(2−z)2)=2−(2−z)2
当z>2时,超出x、y的取值范围,不可能发生
F Z ( z ) = 0 F_Z(z)=0 FZ(z)=0
所以:
F Z ( z ) = { z 2 , 0 ≤ z ≤ 1 1 − ( 2 − z ) 2 2 , 1 ≤ z ≤ 2 0 , 其它 F_Z(z)=\begin{cases} z^2,& 0\leq z\leq 1\\ 1-\dfrac{(2-z)^2}{2},& 1\leq z\leq 2\\ 0,& 其它 \end{cases} FZ(z)=⎩ ⎨ ⎧z2,1−2(2−z)2,0,0≤z≤11≤z≤2其它
求导:
f Z ( z ) = F z ′ ( z ) = { 2 z , 0 ≤ z ≤ 1 4 − 2 z , 1 ≤ z ≤ 2 0 , 其它 f_Z(z)=F_z'(z)=\begin{cases} 2z,& 0\leq z\leq 1\\ 4-2z,& 1\leq z\leq 2\\ 0,& 其它 \end{cases} fZ(z)=Fz′(z)=⎩ ⎨ ⎧2z,4−2z,0,0≤z≤11≤z≤2其它
相关文章:

10.11Python数学基础-多维随机变量及其分布
多维随机变量及其分布 1.二维随机变量及其分布 假设E是随机试验,Ω是样本空间,X、Y是Ω的两个变量;(X,Y)就叫做二维随机变量或二维随机向量。X、Y来自同一个样本空间。 联合分布函数 F ( x , y ) P ( X ≤ x , Y ≤ y ) F(x,y)P(X≤x,Y≤…...
Mysql 数据库备份恢复全攻略)
(四)Mysql 数据库备份恢复全攻略
一、数据库备份 数据库备份目的和数据库故障类型 目的: 当发生故障时,将损失降到最低。保证能够快速从备份数据中恢复,确保数据稳定运行。故障类型: 程序错误:Mysql 服务器端程序故障无法使用。人为误操作:…...

在MySQL 8.0中,如何更好地管理索引以节省空间和提高查询效率?
1. 索引选择与设计 选择合适的列:确保索引覆盖的列是经常用于查询条件、排序或连接操作的列。避免冗余索引:检查并移除重复或不必要的索引。例如,如果已经有一个 INDEX(a, b),那么单独的 INDEX(a) 可能是多余的。使用复合索引&am…...

图形化编程(013)——“面向鼠标指针”积木块
知识回顾 1、舞台和坐标的知识 2、使用坐标控制角色移动 一句俗语:大鱼吃小鱼,小鱼吃虾米,感觉挺有意思的。 这句话说明了自然界中的生存法则,本次分享我与大家共同做一个大鱼吃小鱼的作品。 案例解说: 点击绿旗…...
【Spring】Spring Boot项目创建和目录介绍
文章目录 1 Spring Boot 介绍2 Spring Boot 项目创建注意事项 3. 项目代码和目录介绍pom 文件父工程目录介绍 1 Spring Boot 介绍 Spring 让 Java 程序更加快速、简单和安全,Spring 对于速度、简单性和生产力的关注使其成为世界上最流行的 Java 框架 Spring 官方提…...

第十二章 RabbitMQ之失败消息处理策略
目录 一、引言 二、RepublishMessageRecoverer 实现 2.1. 实现步骤 2.2. 实现代码 2.2.1. 异常交换机队列回收期配置类 2.2.2. 常规交换机队列配置类 2.2.3. 消费者代码 2.2.4. 消费者yml配置 2.2.5. 生产者代码 2.2.6. 生产者yml配置 2.2.7. 运行效果 一、引言 …...

23年408数据结构
第一题: 解析: 第一点,我们要知道顺序存储的特点:优点就是随用随取,就是你想要查询第几个元素可以直接查询出来,时间复杂度就是O(1),缺点就是不适合删除和插入,因为每次删除和插入一…...

vue3ElementPlu表格合并多行
// 单元格合并逻辑 const objectSpanMethod ({ row, rowIndex, columnIndex }) > { const previousMachineModelUniqueId rowIndex > 0 ? tableData.value[rowIndex - 1].machineModel : null; const currentMachineModelUniqueId row.machineModel; // 合并“机型”…...

MySQL数据库 - 索引(上)
目录 1 简介 1.1 索引是什么 1.2 为什么要使用索引 2 索引应该选择哪种数据结构 2.1 HASH 2.2 二叉搜索树 2.3 N叉树(B树) 2.4 B树 3 MySQL的页 3.1 为什么要使用页 3.2 页文件头和页文件尾 3.3 页主体 3.4 页目录 4 B树在MySQL索引中的应…...
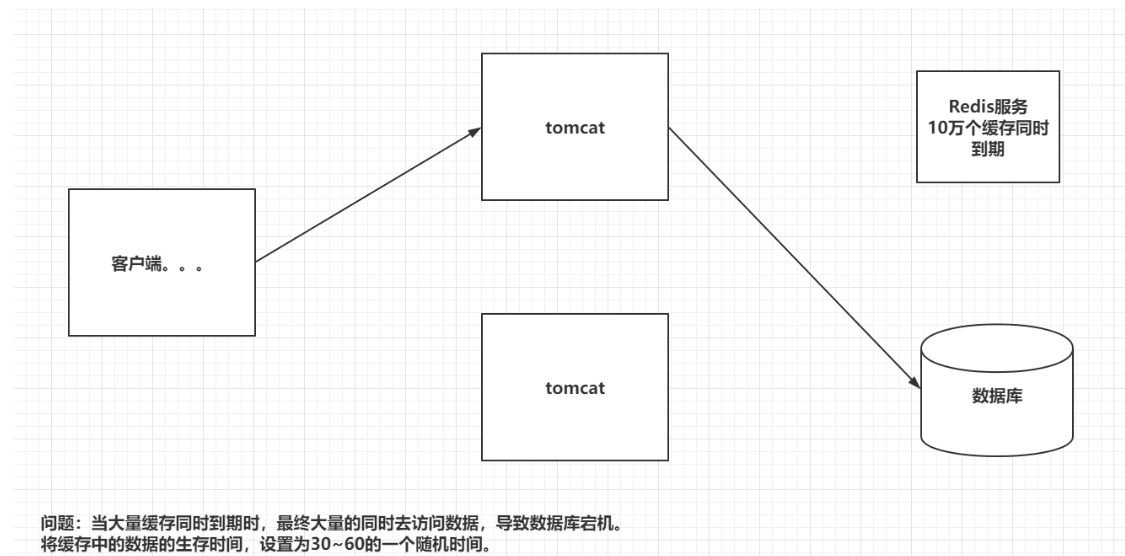
redis与springBoot整合
前提 要实现,使用Redis存储登录状态 需要一个完整的前端后端的项目 前端项目搭建 解压脚手架 安装依赖 配置请求代理 选做: 禁用EsLint语法检查 Vue Admin Template关闭eslint校验,lintOnSave:false设置无效解决办法_lintonsave: false-CSDN博客 …...

YoloV9改进策略:BackBone改进|CAFormer在YoloV9中的创新应用,显著提升目标检测性能
摘要 在目标检测领域,模型性能的提升一直是研究者和开发者们关注的重点。近期,我们尝试将CAFormer模块引入YoloV9模型中,以替换其原有的主干网络,这一创新性的改进带来了显著的性能提升。 CAFormer,作为MetaFormer框架下的一个变体,结合了深度可分离卷积和普通自注意力…...

消防应急物资仓库管理系统
集驰电子消防装备仓库管理系统(DW-S302系统)是一套成熟系统,依托3D技术、大数据、RFID技术、数据库技术、对装备器材进行统一管理,以RFID射频识别技术为核心,构建以物资综合管理为基础,智能分析定位为主要特色功能的装备器材库综合…...

【论文阅读】Semi-Supervised Few-shot Learning via Multi-Factor Clustering
通过多因素聚类的半监督小样本学习 引用:Ling J, Liao L, Yang M, et al. Semi-supervised few-shot learning via multi-factor clustering[C]//Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. 2022: 14564-14573. 论文地址…...

第十三章 RabbitMQ之消息幂等性
目录 一、引言 二、消息幂等解决方案 2.1. 方案一 2.2. 方案二 一、引言 幂等是一个数学概念,用函数表达式来描述是这样的:f(x) f(f(x)) 。在程序开发中,则是指同一个业务,执行一次或多次对业务状态的影响是一致的。有些业务…...
tpcms-master.zip
网盘:https://pan.notestore.cn/s.html?id34https://pan.notestore.cn/s.html?id34...

Spring国际化和Validation
SpringBoot国际化和Validation融合 场景 在应用交互时,可能需要根据客户端得语言来返回不同的语言数据。前端通过参数、请求头等往后端传入locale相关得参数,后端获取参数,根据不同得locale来获取不同得语言得文本信息返回给前端。 实现原…...
②EtherCAT转ModbusTCP, EtherCAT/Ethernet/IP/Profinet/ModbusTCP协议互转工业串口网关
EtherCAT/Ethernet/IP/Profinet/ModbusTCP协议互转工业串口网关https://item.taobao.com/item.htm?ftt&id822721028899 协议转换通信网关 EtherCAT 转 Modbus TCP (接上一章) GW系列型号 配置说明 上载 网线连接电脑到模块上的 WEB 网页设置网口&#…...

【华为HCIP实战课程八】OSPF网络类型及报文类型详解,网络工程师
一、点到点网络类型 1、两台路由器 2、支持广播、组播 P2P(PPP、HDLC、帧中继子接口) 我们需要三个维度考虑 A、是否自动通过组播发现邻居 B、时间(Hello和Dead) C、DR和BDR----多点接入网络需要用到(广播和NBMA) 点到点是组播自动发现邻居,Hello 10S,Dead 40S…...

信息安全工程师(28)机房安全分析与防护
前言 机房安全分析与防护是一个复杂而细致的过程,涉及到物理安全、环境控制、电力供应、数据安全、设备管理、人员管理以及紧急预案等多个方面。 一、机房安全分析 1. 物理安全威胁 非法入侵:未经授权的人员可能通过门窗、通风口等进入机房,…...

大数据处理从零开始————9.MapReduce编程实践之信息过滤之学生成绩统计demo
1.项目目标 1.1 需求概述 现在我们要统计某学校学生的成绩信息,筛选出成绩在60分及以上的学生。 1.2 业务分析 如果我们想实现该需求,可以通过编写一个MapReduce程序,来处理包含学生信息的文本文件,每行包含【学生的姓名&#x…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...

视觉slam十四讲实践部分记录——ch2、ch3
ch2 一、使用g++编译.cpp为可执行文件并运行(P30) g++ helloSLAM.cpp ./a.out运行 二、使用cmake编译 mkdir build cd build cmake .. makeCMakeCache.txt 文件仍然指向旧的目录。这表明在源代码目录中可能还存在旧的 CMakeCache.txt 文件,或者在构建过程中仍然引用了旧的路…...

如何应对敏捷转型中的团队阻力
应对敏捷转型中的团队阻力需要明确沟通敏捷转型目的、提升团队参与感、提供充分的培训与支持、逐步推进敏捷实践、建立清晰的奖励和反馈机制。其中,明确沟通敏捷转型目的尤为关键,团队成员只有清晰理解转型背后的原因和利益,才能降低对变化的…...

永磁同步电机无速度算法--基于卡尔曼滤波器的滑模观测器
一、原理介绍 传统滑模观测器采用如下结构: 传统SMO中LPF会带来相位延迟和幅值衰减,并且需要额外的相位补偿。 采用扩展卡尔曼滤波器代替常用低通滤波器(LPF),可以去除高次谐波,并且不用相位补偿就可以获得一个误差较小的转子位…...
