信息安全数学基础(29) x^2 + y^2 = p
前言
方程 x2+y2=p 是一个涉及整数解和素数 p 的二次方程。这个方程在数论和几何中都有重要的意义,特别是在研究圆的整数点和费马大定理的背景下。
一、定义与背景
方程 x2+y2=p 表示一个平面上的圆,其圆心在原点 (0,0),半径为 p(当 p>0 时)。然而,在这个上下文中,我们更关心的是方程的整数解,即 x 和 y 都是整数。
二、整数解的存在性
- 当 p 为素数时:
- 如果 p=2,则方程变为 x2+y2=2,其整数解为 (x,y)=(1,1),(1,−1),(−1,1),(−1,−1)。
- 如果 p 是形如 4k+1 的素数(其中 k 是整数),则方程有整数解。这是由费马小定理的一个推论得出的,即存在整数 a 和 b 使得 a2+b2=p。
- 如果 p 是形如 4k+3 的素数,则方程没有非零整数解。这是由模4的性质得出的,即任何形如 4k+3 的素数在模4下都余3,而两个整数的平方和不可能模4余3(只能是0, 1, 或2)。
- 当 p 不是素数时:
- 如果 p 是负数,则方程在实数范围内没有解,因为两个实数的平方和不能是负数。
- 如果 p 是正合数,则方程可能有也可能没有整数解,这取决于 p 的因数分解。例如,x2+y2=50 有整数解 (x,y)=(5,5),(5,−5),(−5,5),(−5,−5),(7,1),(7,−1),(−7,1),(−7,−1) 等,因为50可以分解为 5×10 或 2×25,而这些因数都有整数平方根。
三、几何意义
在几何上,方程 x2+y2=p 描述了一个以原点为中心,半径为 p 的圆(当 p>0 时)。然而,在这个问题中,我们更关心的是这个圆上的整数点,即满足方程的整数对 (x,y)。
四、数论意义
在数论中,方程 x2+y2=p 的整数解与费马大定理(Fermat's Last Theorem)有间接的联系。费马大定理断言,对于任何大于2的整数 n,方程 xn+yn=zn 没有正整数解。虽然 x2+y2=p 并不直接涉及 n>2 的情况,但研究这个方程有助于理解整数解在二次方程中的行为,并为更复杂的数论问题提供启示。
五、应用
方程 x2+y2=p 的整数解在密码学、编码理论和计算机科学中有应用。例如,在密码学中,某些加密算法利用了整数解的稀疏性来增强安全性。在编码理论中,整数解可以用于构建具有特定性质的码字。在计算机科学中,研究这个方程有助于开发更高效的算法来解决相关的计算问题。
总结
综上所述,方程 x2+y2=p 是一个涉及整数解和素数 p 的重要二次方程。它在数论、几何和应用数学中都有广泛的应用和深入的研究。
![]() 结语
结语
这个世界就这么不完美
你想得到些什么就不得不失去些什么
!!!

相关文章:

信息安全数学基础(29) x^2 + y^2 = p
前言 方程 x2y2p 是一个涉及整数解和素数 p 的二次方程。这个方程在数论和几何中都有重要的意义,特别是在研究圆的整数点和费马大定理的背景下。 一、定义与背景 方程 x2y2p 表示一个平面上的圆,其圆心在原点 (0,0),半径为 p(当…...

ChatGPT国内中文版镜像网站整理合集(2024/10/06)
一、GPT中文镜像站 ① yixiaai.com 支持GPT4、4o以及o1,支持MJ绘画 ② chat.lify.vip 支持通用全模型,支持文件读取、插件、绘画、AIPPT ③ AI Chat 支持GPT3.5/4,4o以及MJ绘画 1. 什么是镜像站 镜像站(Mirror Siteÿ…...

图文深入理解Oracle DB Scheduler
值此国庆佳节,深宅家中,闲来无事,就多写几篇博文。今天继续宅继续写。本篇图文深入介绍Oracle DB Scheduler。 Oracle为什么要使Scheduler? 答案就是6个字:简化管理任务。 • Scheduler(调度程序&#x…...
实时推送技术实现消息推送)
gin如何具体利用Server-Send-Events(SSE)实时推送技术实现消息推送
目录 业务场景 解决方案 1. 轮询 2. WebSocket 3. SSE(Server-Send-Events) 代码实现 总结 业务场景 在抖音、美团等APP中,我们经常会遇到APP内部的消息推送,如关注的人的动态消息推送、点赞评论互动消息推送以及算法推荐消息推送。这些场景都是…...

写端口-tcp udp不同方式发包和接包
最近一直在学习网络编程,今天把 socket部分做一个总结。 Python 的socket库可以实现不同协议不同地址的发包和收包,无奈资料很少,官方例子有限,大神博客很少提及, 经过一番尝试后,总结以下几点用法以便大家…...

计算机的错误计算(一百二十)
摘要 探讨在许多应用中出现的函数 的计算精度问题。 例1. 考虑在许多应用中出现的函数 计算 不妨在Python下计算: 若用下列Rust代码在线计算: fn f(x: f64) -> f64 {(x.exp() - 1.0) / x }fn main() {let result f(0.9e-13);println!("…...

Spring Boot 中使用 JSON Schema 来校验复杂 JSON 数据
博客主页: 南来_北往 系列专栏:Spring Boot实战 在现代软件开发中,尤其是构建 RESTful API 时,处理 JSON 数据已成为一项基本任务。JSON(JavaScript Object Notation)因其轻量级和易于人类阅读的特点ÿ…...

QT实现Opencv图像处理
案例 基于QT的人脸识别 pro文件需要加以下代码 INCLUDEPATH E:/opencv/opencv3.4-qt-intall/install/include INCLUDEPATH E:/opencv/opencv3.4-qt-intall/install/include/opencv INCLUDEPATH E:/opencv/opencv3.4-qt-intall/install/include/opencv2 LIBS E:/opencv/o…...
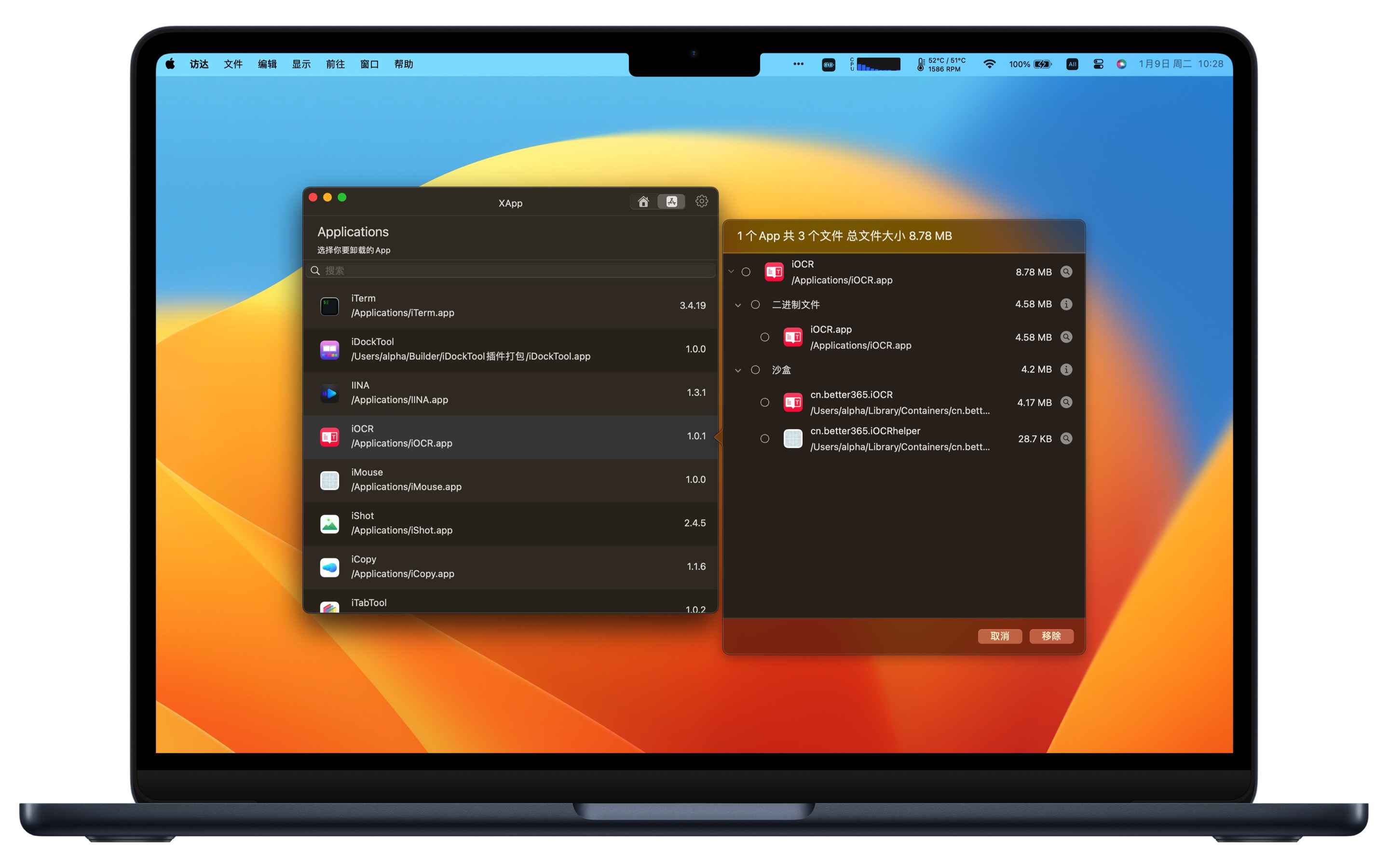
刚转Mac的新手如何卸载不需要的应用程序
最开始转Mac系统的时候很是苦恼,到底该怎么卸载App啊,App直接拖到废纸篓真的能卸载干净吗,卸载App时会不会留下一些文件残留,慢慢的会不会占满内存,于是我找到了一个免费的卸载工具——XApp。 这是一款Mac应用程序卸载…...

Unity 3d 继承MonoBahaviour的单例
在使用Unity3d开发游戏或做客户端项目时,单例是最常见的模式之一,他简单了类的创建,在代码中可以直接调用。下面是两个例子,代码两种不同类型的单例,一个是基本类的单例基类,不是unity MonoBehaviour的类都…...

grafana version 11.1.0 设置Y轴刻度为1
grafana 版本 # /usr/share/grafana/bin/grafana --version grafana version 11.1.0设置轴 Axis 搜索 Standard options 在"Decimals"中输入0,确保只显示整数...

Elasticsearch的安装与配置
注意:elasticsearch 禁止安装在/root路径下! 1、创建用户组 groupadd elastic 2、创建用户 useradd es -d /home/es -g elastic echo es | passwd es --stdin 3、给新创建的用户进行授权 chown -R es:elastic /home/es chmod -R 775 /home/es 4…...

win0删除 Windows.old
参考:https://blog.csdn.net/xitongzhijia_abc/article/details/126270452 win10如下所示: 打开 设置–>系统—>存储...

常见IDE及其编译器的讲解
IDE 意思是:集成开发环境 常见的IDE有哪些? eg. devC,VS2022,xcode,codeblocks,clion常见编译器有哪些? eg.msvc,gcc,clang微软的底层编译器是msvc苹果的底层编译器是clang IDE编译器特点devC集成了gcc小巧,工具简单&…...

用SQLyog连接mysql提示2058错误
1)在cmd下(必须是这个,不能是gitbash) // step1:修改下数据库 C:\Users\elex>mysql -uroot -p Enter password: **** Welcome to the MySQL monitor. Commands end with ; or \g. Your MySQL connection id is 97 Server version: 8.1.0 MySQL Community Server - GPLCopy…...

Web集群服务-Nginx
1. web服务 1. WEB服务:网站服务,部署并启动了这个服务,你就可以搭建一个网站 2. WEB中间件: 等同于WEB服务 3. 中间件:范围更加广泛,指的负载均衡之后的服务 4. 数据库中间件:数据库缓存,消息对列 2. 极速上手指南 nginx官网: nginx documentation 2.1 配置yum源 vim /etc/…...

获取时隔半个钟的三天
摘要: 今天遇到需求是配送时间,时隔半个钟的排线!所以需要拼接时间!例如2024-10-08 14:30,2024-10-08 15:00,2024-10-08 15:30 <el-form-item label"配送时间&a…...

构建可以ssh连接的容器镜像
构建可以ssh连接的容器镜像 构建可以通过ssh进行连接容器镜像,实现远程登录容器的目的。 ubuntu ssh容器镜像 你可以使用以下Dockerfile来构建一个可以SSH的容器镜像: FROM ubuntu:20.04MAINTAINER lldhsds# 配置apt国内源 COPY sources.list /etc/a…...

数据库中JOIN的用法?
在数据库中,JOIN 操作用于结合来自两个或多个表的数据,基于它们之间的相关列。JOIN 是关系数据库查询中一个非常重要的功能,允许你从多个表中提取相关的数据。以下是几种常见的 JOIN 类型及其用法: INNER JOIN: 返回两个表中匹配的…...

java项目之纺织品企业财务管理系统源码(springboot+vue+mysql)
风定落花生,歌声逐流水,大家好我是风歌,混迹在java圈的辛苦码农。今天要和大家聊的是一款基于springboot的纺织品企业财务管理系统。项目源码以及部署相关请联系风歌,文末附上联系信息 。 项目简介: 基于spring boot…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

HubSpot推出与ChatGPT的深度集成引发兴奋与担忧
上周三,HubSpot宣布已构建与ChatGPT的深度集成,这一消息在HubSpot用户和营销技术观察者中引发了极大的兴奋,但同时也存在一些关于数据安全的担忧。 许多网络声音声称,这对SaaS应用程序和人工智能而言是一场范式转变。 但向任何技…...

高防服务器价格高原因分析
高防服务器的价格较高,主要是由于其特殊的防御机制、硬件配置、运营维护等多方面的综合成本。以下从技术、资源和服务三个维度详细解析高防服务器昂贵的原因: 一、硬件与技术投入 大带宽需求 DDoS攻击通过占用大量带宽资源瘫痪目标服务器,因此…...

AxureRP-Pro-Beta-Setup_114413.exe (6.0.0.2887)
Name:3ddown Serial:FiCGEezgdGoYILo8U/2MFyCWj0jZoJc/sziRRj2/ENvtEq7w1RH97k5MWctqVHA 注册用户名:Axure 序列号:8t3Yk/zu4cX601/seX6wBZgYRVj/lkC2PICCdO4sFKCCLx8mcCnccoylVb40lP...

Linux安全加固:从攻防视角构建系统免疫
Linux安全加固:从攻防视角构建系统免疫 构建坚不可摧的数字堡垒 引言:攻防对抗的新纪元 在日益复杂的网络威胁环境中,Linux系统安全已从被动防御转向主动免疫。2023年全球网络安全报告显示,高级持续性威胁(APT)攻击同比增长65%,平均入侵停留时间缩短至48小时。本章将从…...

yaml读取写入常见错误 (‘cannot represent an object‘, 117)
错误一:yaml.representer.RepresenterError: (‘cannot represent an object’, 117) 出现这个问题一直没找到原因,后面把yaml.safe_dump直接替换成yaml.dump,确实能保存,但出现乱码: 放弃yaml.dump,又切…...

生信服务器 | 做生信为什么推荐使用Linux服务器?
原文链接:生信服务器 | 做生信为什么推荐使用Linux服务器? 一、 做生信为什么推荐使用服务器? 大家好,我是小杜。在做生信分析的同学,或是将接触学习生信分析的同学,<font style"color:rgb(53, 1…...

02-性能方案设计
需求分析与测试设计 根据具体的性能测试需求,确定测试类型,以及压测的模块(web/mysql/redis/系统整体)前期要与相关人员充分沟通,初步确定压测方案及具体的性能指标QA完成性能测试设计后,需产出测试方案文档发送邮件到项目组&…...
