矩阵等价、向量组等价、线性方程组同解与公共解的关系
矩阵等价
矩阵 A 、 B 等价 ⇔ 两矩阵秩相等 R ( A ) = R ( B ) ⇔ 每个矩阵的行秩等于列秩,两个矩阵的行秩与列秩分别相等 ⇔ 若行满秩则列向量组等价 ⇔ 若列满秩则行向量组等价 \begin{align} 矩阵A、B等价\\ &\Leftrightarrow 两矩阵秩相等R(A)=R(B)\\ &\Leftrightarrow 每个矩阵的行秩等于列秩,两个矩阵的行秩与列秩分别相等\\ &\Leftrightarrow 若行满秩则列向量组等价\\ &\Leftrightarrow 若列满秩则行向量组等价 \end{align} 矩阵A、B等价⇔两矩阵秩相等R(A)=R(B)⇔每个矩阵的行秩等于列秩,两个矩阵的行秩与列秩分别相等⇔若行满秩则列向量组等价⇔若列满秩则行向量组等价
向量组等价
向量组 A 、 B 等价 ⇔ A 与 B 可相互线性表示出(两个向量组不同秩一定不等价,同秩也不一定等价) ⇔ 行向量组等价即两个行向量组可以通过行初等变换相互转换 ⇔ 列向量组等价即两个列向量组可以通过列初等变换相互转换 \begin{align} 向量组A、B等价\\ &\Leftrightarrow A与B可相互线性表示出(两个向量组不同秩一定不等价,同秩也不一定等价)\\ &\Leftrightarrow 行向量组等价即两个行向量组可以通过行初等变换相互转换\\ &\Leftrightarrow 列向量组等价即两个列向量组可以通过列初等变换相互转换 \end{align} 向量组A、B等价⇔A与B可相互线性表示出(两个向量组不同秩一定不等价,同秩也不一定等价)⇔行向量组等价即两个行向量组可以通过行初等变换相互转换⇔列向量组等价即两个列向量组可以通过列初等变换相互转换
线性方程组公共解
线性方程组 A x = ξ 与 B x = η 的公共解即 { A x = ξ B x = η 的解 线性方程组Ax=\xi 与Bx=\eta的公共解即\begin{cases} Ax=\xi\\ Bx=\eta\\ \end{cases}的解 线性方程组Ax=ξ与Bx=η的公共解即{Ax=ξBx=η的解
线性方程组同解
线性方程组 A x = ξ 与 B x = η 同解 ⇔ ( A , ξ ) 可通过行初等变换变为 ( B , η ) ⇔ A 与 B 行向量组等价 ⇒ A 与 B 行等秩 ⇒ A 与 B 等价 \begin{align} 线性方程组Ax=\xi 与Bx=\eta同解\\ &\Leftrightarrow (A,\xi)可通过行初等变换变为(B,\eta)\\ &\Leftrightarrow A与B行向量组等价\\ &\Rightarrow A与B行等秩\\ &\Rightarrow A与B等价\end{align} 线性方程组Ax=ξ与Bx=η同解⇔(A,ξ)可通过行初等变换变为(B,η)⇔A与B行向量组等价⇒A与B行等秩⇒A与B等价
A T A x = 0 与 A x = 0 同解 A k x = 0 与 A x = 0 同解 A n + 1 x = 0 与 A n x = 0 同解 \begin{align} &A^TAx=0与Ax=0同解\\ &A^kx=0与Ax=0同解\\ &A^{n+1}x=0与A^nx=0同解\end{align} ATAx=0与Ax=0同解Akx=0与Ax=0同解An+1x=0与Anx=0同解
相关文章:

矩阵等价、向量组等价、线性方程组同解与公共解的关系
矩阵等价 矩阵 A 、 B 等价 ⇔ 两矩阵秩相等 R ( A ) R ( B ) ⇔ 每个矩阵的行秩等于列秩,两个矩阵的行秩与列秩分别相等 ⇔ 若行满秩则列向量组等价 ⇔ 若列满秩则行向量组等价 \begin{align} 矩阵A、B等价\\ &\Leftrightarrow 两矩阵秩相等R(A)R(B)\\ &\…...

[Linux] Linux 进程程序替换
标题:[Linux] Linux 进程程序替换 个人主页水墨不写bug (图片来源于网络) 目录 O、前言 一、进程程序替换的直观现象(什么是进程程序替换?) 二、进程程序替换的原理 三、进程程序替换的函数(…...

【Linux系统编程】第三十一弹---深入理解静态库:从零开始制作与高效使用的完全指南
✨个人主页: 熬夜学编程的小林 💗系列专栏: 【C语言详解】 【数据结构详解】【C详解】【Linux系统编程】 目录 1、静态库 1.1、怎么做静态库 1.2、怎么使用静态库 1、静态库 1.1、怎么做静态库 在Linux环境下,通常使用GCC&am…...
FFmpeg 简介及其下载安装步骤
目录 一、FFmpeg 简介 二、FFmpeg 安装步骤 2.1 打开官网 2.2 选择FFmpeg系统版本 2.3 下载FFmpeg压缩包 2.4 将下载好的压缩包进行解压 2.5 设置环境变量 2.5.1 在搜索栏中搜索【环境变量】,然后单击将其打开 2.5.2 找到系统变量中的【Path】,点…...

使用CSS+SVG实现加载动画
使用CSSSVG实现加载动画 效果展示 CSS知识点 SVG元素使用SVG相关CSS属性运用 整体页面布局 <section><div class"box"><div class"loader"><svg><circle cx"40" cy"40" r"40"></circl…...
的未来发展:智能互联时代的到来)
物联网(IoT)的未来发展:智能互联时代的到来
物联网(IoT)的未来发展:智能互联时代的到来 物联网(IoT)正在迅速改变我们与世界互动的方式。无论是智能家居、智慧城市,还是工业自动化,物联网技术通过设备互联、数据采集和智能控制࿰…...
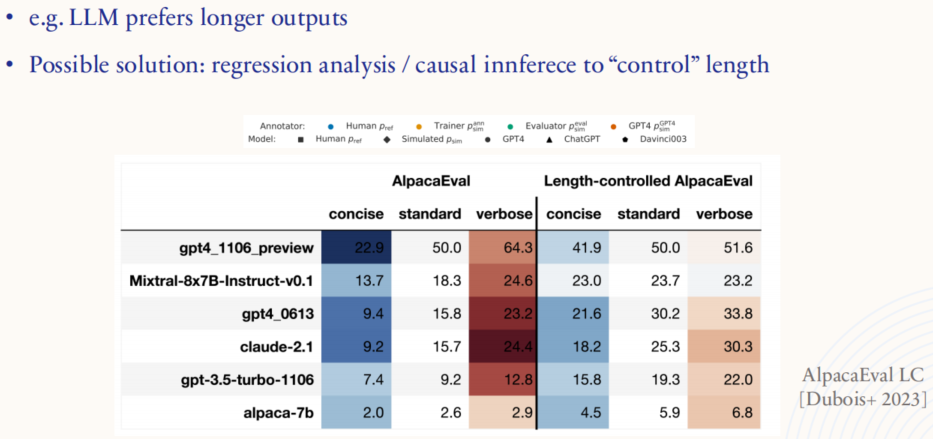
斯坦福 CS229 I 机器学习 I 构建大型语言模型 (LLMs)
1. Pretraining -> GPT3 1.1. Task & loss 1.1.1. 训练 LLMs 时的关键点 对于 LLMs 的训练来说,Architecture(架构)、Training algorithm/loss(训练算法/损失函数)、Data(数据)、Evalu…...

Java->排序
目录 一、排序 1.概念 2.常见的排序算法 二、常见排序算法的实现 1.插入排序 1.1直接插入排序 1.2希尔排序(缩小增量法) 1.3直接插入排序和希尔排序的耗时比较 2.选择排序 2.1直接选择排序 2.2堆排序 2.3直接选择排序与堆排序的耗时比较 3.交换排序 3.1冒泡排序…...

linux 大小写转换
var"TM_card_INFo" # 把变量中的第一个字符换成大写 echo ${var^} # 把变量中的所有小写字母,全部替换为大写 echo ${var^^} # 把变量中的第一个字符换成小写 echo ${var,} # 把变量中的所有大写字母,全部替换为小写 echo ${var,,} 参考…...

Linux——传输层协议
目录 一再谈端口号 1端口号范围划分 2两个问题 3理解进程与端口号的关系 二UDP协议 1格式 2特点 3进一步理解 3.1关于UDP报头 3.2关于报文 4基于UDP的应用层协议 三TCP协议 1格式 2TCP基本通信 2.1关于可靠性 2.2TCP通信模式 3超时重传 4连接管理 4.1建立…...

centos系列,yum部署jenkins2.479.1,2024年长期支持版本
centos系列,yum部署jenkins2.479.1,2024年长期支持版本 0、介绍 注意:jenkins建议安装LTS长期支持版本,而不是安装每周更新版本,jenkins安装指定版本 openjdk官网下载 Index of /jenkins/redhat-stable/ | 清华大学开…...

正则表达式-“三剑客”(grep、sed、awk)
1.3正则表达式 正则表达式描述了一种字符串匹配的模式,可以用来检查一个串是否含有某种子串,将匹配的子串替换或者从某个串中取出符号某个条件的子串等,在linux中代表自定义的模式模版,linux工具可以用正则表达式过滤文本。Linux…...

数智时代的新航向:The Open Group 2024生态系统架构·可持续发展年度大会邀您共筑AI数字新时代
在全球可持续发展和数字化转型双重驱动下,企业正面临着前所未有的挑战与机遇。如何在激烈的市场竞争中,实现业务增长的同时,履行社会责任,达成可持续发展的目标?The Open Group 2024生态系统架构可持续发展年度大会将于…...

TensorFlow 的核心概念
TensorFlow 是一个开源的机器学习框架,由 Google 开发和维护。它提供了一个强大的工具集,用于构建和训练各种机器学习模型。 TensorFlow 的核心概念是计算图(Computational Graph)。计算图由节点(Nodes)和…...

SpringBoot教程(二十四) | SpringBoot实现分布式定时任务之Quartz(动态新增、修改等操作)
SpringBoot教程(二十四) | SpringBoot实现分布式定时任务之Quartz(动态新增、修改等操作) 前言数据库脚本创建需要被调度的方法创建相关实体类创建业务层接口创建业务层实现类控制层类测试结果 前言 我这边的SpringBoot的版本为2…...

Matlab详细学习教程 MATLAB使用教程与知识点总结
Matlab语言教程 章节目录 一、Matlab简介与基础操作 二、变量与数据类型 三、矩阵与数组操作 四、基本数学运算与函数 五、图形绘制与数据可视化 六、控制流与逻辑运算 七、脚本与函数编写 八、数据导入与导出 九、Matlab应用实例分析 一、Matlab简介与基础操作 重点内容知识…...

【ELKB】Kibana使用
搭建好ELKB后访问地址:http://localhost:5601 输入账号密码登录以后 左侧导航有home、Analysis、Enterprise search 、Observability、Security、Management home:首页Analysis:工具来分析及可视化数据Enterprise search:企业级搜…...

ChatGPT免费使用:人工智能在现代社会中的作用
随着人工智能技术的不断发展,越来越多的应用程序和工具开始使用GPT作为其语言模型。但是,这些应用程序和工具是否收费?如果是免费的,那么他们是如何盈利的?在本文中,我们将探讨ChatGPT免费使用的背后原理&a…...
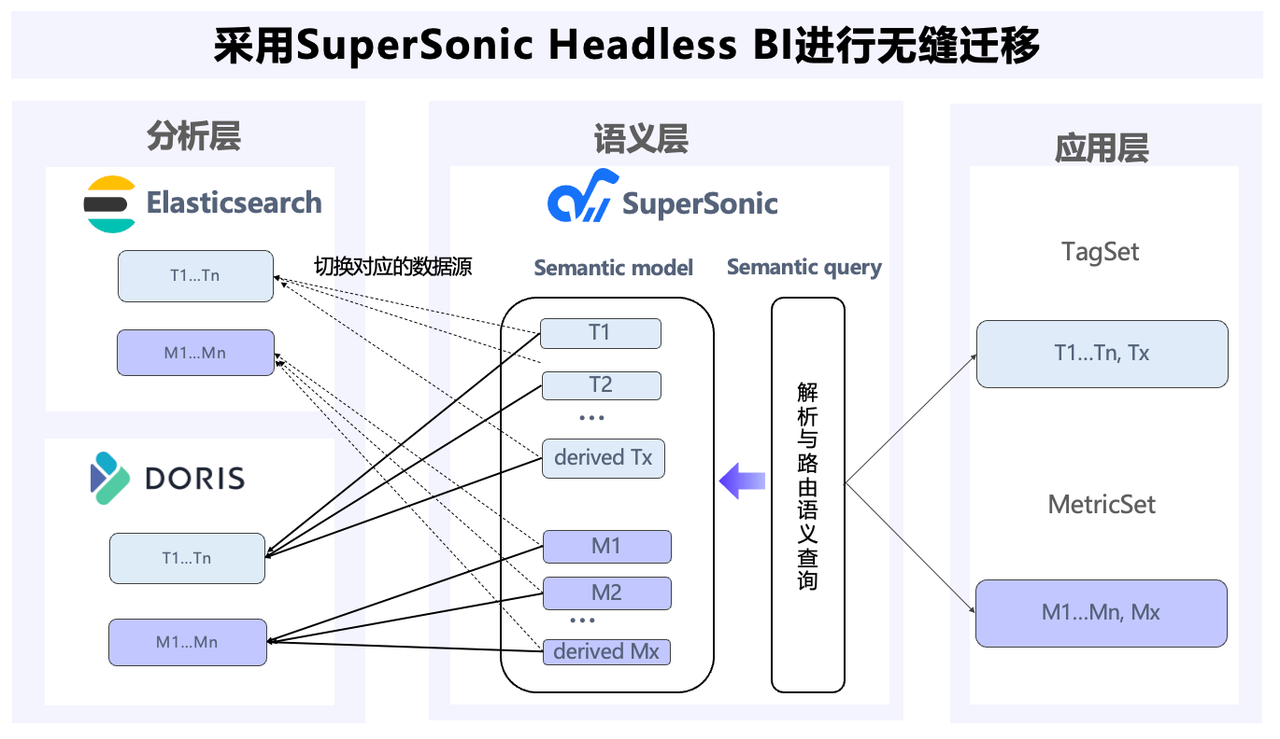
腾讯音乐:从 Elasticsearch 到 Apache Doris 内容库升级,统一搜索分析引擎,成本直降 80%
导读: 为满足更严苛数据分析的需求,腾讯音乐借助 Apache Doris 替代了 Elasticsearch 集群,统一了内容库数据平台的内容搜索和分析引擎。并基于 Doris 倒排索引和全文检索的能力,支持了复杂的自定义标签计算,实现秒级查…...

CubeMX的FreeRTOS学习
一、FreeRTOS的介绍 什么是FreeRTOS? Free即免费的,RTOS的全称是Real Time Operating system,中文就是实时操作系统。 注意:RTOS不是指某一个确定的系统,而是指一类的操作系统。比如:us/OS,FreeRTOS&…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...

python报错No module named ‘tensorflow.keras‘
是由于不同版本的tensorflow下的keras所在的路径不同,结合所安装的tensorflow的目录结构修改from语句即可。 原语句: from tensorflow.keras.layers import Conv1D, MaxPooling1D, LSTM, Dense 修改后: from tensorflow.python.keras.lay…...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...

return this;返回的是谁
一个审批系统的示例来演示责任链模式的实现。假设公司需要处理不同金额的采购申请,不同级别的经理有不同的审批权限: // 抽象处理者:审批者 abstract class Approver {protected Approver successor; // 下一个处理者// 设置下一个处理者pub…...
