C++——AVL树
文章目录
- 一、AVL树的概念
- 二、AVL树的实现
- 1. AVL树的结构
- 2. AVL树的插⼊
- 2.1 AVL树插⼊⼀个值的⼤概过程
- 2.2 平衡因⼦更新
- 更新原则
- 更新停止条件
- 2.3 插⼊结点及更新平衡因⼦的代码实现
- 3. 旋转
- 旋转的原则
- 右单旋
- 左单旋
- 左右双旋
- 右左双旋
- 4.高度
- 5.结点个数
- 6.判断是否是AVL树
- 7. 中序遍历
- 8.查找
- 三、源代码
- AVL.h
- test.cpp
一、AVL树的概念
AVL树是最先发明的自平衡⼆叉查找树,AVL是⼀颗空树,或者具备下列性质的⼆叉搜索树:
它的左右子树都是AV树,且左右子树的高度差的绝对值不超过1。
AVL树是⼀颗高度平衡搜索⼆叉树, 通过控制高度差去控制平衡。
- AVL树得名于它的发明者G. M. Adelson-Velsky和E. M. Landis是两个前苏联的科学家,他们在1962年的论文《An algorithm for the organization of information》中发表了它。
- AVL树实现这里我们引入⼀个平衡因子(balance factor)的概念,每个结点都有⼀个平衡因子,任何
结点的平衡因子等于右子树的高度减去左子树的高度,也就是说任何结点的平衡因子等于0/1/-1,
AVL树并不是必须要平衡因子,但是有了平衡因子可以更方便我们去进行观察和控制树是否平衡, 就像⼀个风向标⼀样。 - 思考⼀下为什么AVL树是高度平衡搜索⼆叉树,要求高度差不超过1,而不是高度差是0呢?0不是更好的平衡吗?画画图分析我们发现,不是不想这样设计,而是有些情况是做不到高度差是0的。⽐如⼀棵树是2个结点,4个结点等情况下,高度差最好就是1,无法作为高度差是0。
- AVL树整体结点数量和分布和完全⼆叉树类似,⾼度可以控制在logN ,那么增删查改的效率也可 以控制在O(logN) ,相⽐⼆叉搜索树有了本质的提升。


二、AVL树的实现
1. AVL树的结构
#pragma once
#include<iostream>
using namespace std;
template<class K, class V>
struct AVLTreeNode
{// 需要parent指针,后续更新平衡因子可以看到pair<K, V> _kv;AVLTreeNode<K, V>* _left;AVLTreeNode<K, V>* _right;AVLTreeNode<K, V>* _parent;int _bf; // balance factorAVLTreeNode(const pair<K, V>& kv):_kv(kv), _left(nullptr), _right(nullptr), _parent(nullptr), _bf(0){}
};
template<class K, class V>
class AVLTree
{typedef AVLTreeNode<K, V> Node;
public:
private:Node * _root = nullptr;
};
2. AVL树的插⼊
2.1 AVL树插⼊⼀个值的⼤概过程
- 插⼊⼀个值按⼆叉搜索树规则进⾏插⼊。
- 新增结点以后,只会影响祖先结点的⾼度,也就是可能会影响部分祖先结点的平衡因⼦,所以更新从新增结点->根结点路径上的平衡因⼦,实际中最坏情况下要更新到根,有些情况更新到中间就可以停⽌了,具体情况我们下⾯再详细分析。
- 更新平衡因⼦过程中没有出现问题,则插⼊结束。
- 更新平衡因⼦过程中出现不平衡,对不平衡⼦树旋转,旋转后本质调平衡的同时,本质降低了⼦树的⾼度,不会再影响上⼀层,所以插⼊结束。
2.2 平衡因⼦更新
更新原则
- 平衡因子 = 右子树高度-左子树高度
- 只有子树高度变化才会影响当前结点平衡因子
- 插入结点,会增加高度,所以新增结点在parent的右子树,parent的平衡因子++,新增结点在
parent的左子树,parent平衡因子 - - - parent所在子树的高度是否变化决定了是否会继续往上更新
更新停止条件
- 更新后parent的平衡因子等于0,更新中parent的平衡因子变化为-1->0 或者 1->0,说明更新前 parent子树⼀边高⼀边低,新增的结点插入在低的那边,插入后parent所在的子树高度不变,不会影响parent的父亲结点的平衡因子,更新结束。
- 更新后parent的平衡因子等于1 或 -1,更新前更新中parent的平衡因子变化为0->1 或者 0->-1,说明更新前parent子树两边⼀样高,新增的插入结点后,parent所在的子树⼀边高⼀边低,parent所在的子树符合平衡要求,但是高度增加了1,会影响parent的父亲结点的平衡因子,所以要继续向上 更新。
- 更新后parent的平衡因子等于2 或 -2,更新前更新中parent的平衡因子变化为1->2 或者 -1->-2,说明更新前parent子树⼀边高⼀边低,新增的插入结点在高的那边,parent所在的子树高的那边更高了,破坏了平衡,parent所在的子树不符合平衡要求,需要旋转处理,旋转的⽬标有两个:1、把parent子树旋转平衡。2、降低parent子树的高度,恢复到插入结点以前的高度。所以旋转后也不需要继续往上更新,插入结束。
更新到10结点,平衡因子为2,10所在的子树已经不平衡,需要旋转处理

更新到中间结点,3为根的子树高度不变,不会影响上⼀层,更新结束

最坏更新到根停⽌

2.3 插⼊结点及更新平衡因⼦的代码实现
bool Insert(const pair<K, V>& kv)
{if (_root == nullptr){_root = new Node(kv);return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(kv);if (parent->_kv.first < kv.first){parent->_right = cur;}else{parent->_left = cur;}cur->_parent = parent;while (parent){if (parent->_left == cur){parent->_bf--;}else{parent->_bf++;}if (parent->_bf == 0){break;}else if (parent->_bf == 1 || parent->_bf == -1){//继续向上更新cur = parent;parent = parent->_parent;}else if (parent->_bf == 2 || parent->_bf == -2){//旋转//右单旋if (parent->_bf == -2 && cur->_bf == -1){RotateR(parent);}//左单旋else if (parent->_bf == 2 && cur->_bf == 1){RotateL(parent);}else if (parent->_bf == -2 && cur->_bf == 1){//左右旋RotateLR(parent);}else if (parent->_bf == 2 && cur->_bf == -1){//右左旋RotateRL(parent);}else{assert(false);}break;}else{assert(false);}}return true;
}
3. 旋转
旋转的原则
- 保持搜索树的规则
- 让旋转的树从不满⾜变平衡,其次降低旋转树的⾼度
旋转总共分为四种,左单旋/右单旋/左右双旋/右左双旋
右单旋
- 本图1展⽰的是10为根的树,有a/b/c抽象为三棵高度为h的子树(h>=0),a/b/c均符合AVL树的要求。10可能是整棵树的根,也可能是⼀个整棵树中局部的子树的根。这里a/b/c是高度为h的子树,
是⼀种概括抽象表示,他代表了所有右单旋的场景,实际右单旋形态有很多种,具体图2/图3/图4/ 图5进行了详细描述。 - 在a子树中插入⼀个新结点,导致a子树的高度从h变成h+1,不断向上更新平衡因子,导致10的平
衡因子从-1变成-2,10为根的树左右高度差超过1,违反平衡规则。10为根的树左边太高了,需要 往右边旋转,控制两棵树的平衡。 - 旋转核心步骤,因为5 < b子树的值 < 10,将b变成10的左子树,10变成5的右子树,5变成这棵树新的根,符合搜索树的规则,控制了平衡,同时这棵的高度恢复到了插入之前的h+2,符合旋转原
则。如果插入之前10整棵树的⼀个局部子树,旋转后不会再影响上⼀层,插入结束了。





//右旋
void RotateR(Node* parent)
{Node* subL = parent->_left;Node* subLR = subL->_right;Node* Pparent = parent->_parent;if (subLR){subLR->_parent = parent;}subL->_right = parent;parent->_parent = subL;parent->_left = subLR;if (Pparent == nullptr){_root = subL;subL->_parent = nullptr;}else{if (Pparent->_left == parent){Pparent->_left = subL;}else{Pparent->_right = subL;}subL->_parent = Pparent;}parent->_bf = 0;subL->_bf = 0;}
左单旋
- 本图6展示的是10为根的树,有a/b/c抽象为三棵高度为h的子树(h>=0),a/b/c均符合AVL树的要
求。10可能是整棵树的根,也可能是⼀个整棵树中局部的子树的根。这里a/b/c是高度为h的子树,
是⼀种概括抽象表示,他代表了所有右单旋的场景,实际右单旋形态有很多种,具体跟上⾯左旋类似。 - 在a子树中插入⼀个新结点,导致a子树的高度从h变成h+1,不断向上更新平衡因子,导致10的平
衡因子从1变成2,10为根的树左右高度差超过1,违反平衡规则。10为根的树右边太高了,需要往 左边旋转,控制两棵树的平衡。 - 旋转核心步骤,因为10 < b子树的值 < 15,将b变成10的右子树,10变成15的左子树,15变成这棵树新的根,符合搜索树的规则,控制了平衡,同时这棵的高度恢复到了插入之前的h+2,符合旋转原则。如果插入之前10整棵树的⼀个局部子树,旋转后不会再影响上⼀层,插入结束了。

//左旋
void RotateL(Node* parent)
{Node* subR = parent->_right;Node* subRL = subR->_left;Node* Pparent = parent->_parent;if (subRL){subRL->_parent = parent;}subR->_left = parent;parent->_parent = subR;parent->_right = subRL;if (Pparent == nullptr){_root = subR;subR->_parent = nullptr;}else{if (Pparent->_left == parent){Pparent->_left = subR;}else{Pparent->_right = subR;}subR->_parent = Pparent;}parent->_bf = 0;subR->_bf = 0;
}
左右双旋
通过图7和图8可以看到,左边高时,如果插入位置不是在a子树,而是插入在b子树,b子树高度从h变成h+1,引发旋转,右单旋无法解决问题,右单旋后,我们的树依旧不平衡。右单旋解决的纯粹的左边高,但是插入在b子树中,10为跟的子树不再是单纯的左边高,对于10是左边高,但是对于5是右边高,需要用两次旋转才能解决,以5为旋转点进行⼀个左单旋,以10为旋转点进行⼀个右单旋,这棵树这棵树就平衡了。


图7和图8分别为左右双旋中h=0和h=1具体场景分析,下面我们将a/b/c子树抽象为高度h的AVL子树进行分析,另外我们需要把b子树的细节进⼀步展开为8和左子树高度为h-1的e和f子树,因为我们要对b的父亲5为旋转点进行左单旋,左单旋需要动b树中的左子树。b子树中新增结点的位置不同,平衡因子更新的细节也不同,通过观察8的平衡因子不同,这里我们要分三个场景讨论。
- 场景1:h >= 1时,新增结点插⼊在e子树,e子树高度从h-1变为h并不断更新8->5->10平衡因子,引发旋转,其中8的平衡因子为-1,旋转后8和5平衡因子为0,10平衡因子为1。
- 场景2:h >=1时,新增结点插⼊在f子树,f子树高度从h-1变为h并不断更新8->5->10平衡因子,引发旋转,其中8的平衡因子为1,旋转后8和10平衡因子为0,5平衡因子为-1。
- 场景3:h == 0时,a/b/c都是空树,b⾃⼰就是⼀个新增结点,不断更新5->10平衡因子,引发旋转,其中8的平衡因子为0,旋转后8和10和5平衡因子均为0。

//左右旋
void RotateLR(Node* parent)
{//subL subLR parentNode* subL = parent->_left;Node* subLR = subL->_right;int bf = subLR->_bf;RotateL(subL);RotateR(parent);if (bf == 0){subL->_bf = 0;subLR->_bf = 0;parent->_bf = 0;}else if (bf == 1){subL->_bf = -1;subLR->_bf = 0;parent->_bf = 0;}else if (bf == -1){subL->_bf = 0;subLR->_bf = 0;parent->_bf = 1;}else{assert(false);}
}
右左双旋
跟左右双旋类似,下⾯我们将a/b/c子树抽象为⾼度h的AVL子树进⾏分析,另外我们需要把b子树的细节进⼀步展开为12和左子树⾼度为h-1的e和f子树,因为我们要对b的⽗亲15为旋转点进⾏右单旋,右单旋需要动b树中的右子树。b子树中新增结点的位置不同,平衡因子更新的细节也不同,通过观察12的平衡因子不同,这⾥我们要分三个场景讨论。
- 场景1:h >=1时,新增结点插⼊在e子树,e子树⾼度从h-1变为h并不断更新12->15->10平衡因子,引发旋转,其中12的平衡因子为-1,旋转后10和12平衡因子为0,15平衡因子为1。
- 场景2:h >=1时,新增结点插⼊在f子树,f子树⾼度从h-1变为h并不断更新12->15->10平衡因子,引发旋转,其中12的平衡因子为1,旋转后15和12平衡因子为0,10平衡因子为-1。
- 场景3:h ==0时,a/b/c都是空树,b自己就是⼀个新增结点,不断更新15->10平衡因子,引发旋转,其中12的平衡因子为0,旋转后10和12和15平衡因子均为0。

//右左旋
void RotateRL(Node* parent)
{//parent subRL subRNode* subR = parent->_right;Node* subRL = subR->_left;int bf = subRL->_bf;RotateR(subR);RotateL(parent);if (bf == 0){subR->_bf = 0;subRL->_bf = 0;parent->_bf = 0;}else if (bf == 1){subR->_bf = 0;subRL->_bf = 0;parent->_bf = -1;}else if (bf == -1){subR->_bf = 1;subRL->_bf = 0;parent->_bf = 0;}else{assert(false);}
}4.高度
//高度
int _Height(Node* root)
{if (root == nullptr){return 0;}int left = _Height(root->_left);int right = _Height(root->_right);return left > right ? left + 1 : right + 1;
}
5.结点个数
//结点个数
int _Size(Node* root)
{if (root == nullptr){return 0;}return _Size(root->_left) + _Size(root->_right) + 1;
}
6.判断是否是AVL树
//判断
bool _IsBalanceTree(Node* root)
{//空树也是AVL树if (root == nullptr){return true;}int leftHeight = _Height(root->_left);int rightHeight = _Height(root->_right);int diff = rightHeight - leftHeight;if (abs(diff) >= 2){cout << root->_kv.first << "高度差异常" << endl;return false;}if (root->_bf != diff){cout << root->_kv.first << "平衡因子异常" << endl;return false;}return _IsBalanceTree(root->_left) && _IsBalanceTree(root->_right);
}
7. 中序遍历
//中序遍历
void _InOrder(Node* root)
{if (root == nullptr){return;}_InOrder(root->_left);cout << root->_kv.first << ":" << root->_kv.second << endl;_InOrder(root->_right);
}
8.查找
Node* Find(const K& key)
{Node* cur = _root;while (cur){if (cur->_kv.first < key){cur = cur->_right;}else if (cur->_kv.first > key){cur = cur->_left;}else{return cur;}}return nullptr;
}
三、源代码
AVL.h
#pragma once
#include <iostream>
#include <assert.h>
using namespace std;template<class K,class V>
struct AVLTreeNode
{AVLTreeNode<K,V>* _left;AVLTreeNode<K,V>* _right;AVLTreeNode<K,V>* _parent;pair<K,V> _kv;int _bf;//节点的平衡因子AVLTreeNode(const pair<K, V>& kv):_left(nullptr),_right(nullptr),_parent(nullptr),_kv(kv),_bf(0){}
};template<class K, class V>
class AVLTree
{typedef AVLTreeNode<K, V> Node;
public:bool Insert(const pair<K, V>& kv){if (_root == nullptr){_root = new Node(kv);return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(kv);if (parent->_kv.first < kv.first){parent->_right = cur;}else{parent->_left = cur;}cur->_parent = parent;while (parent){if (parent->_left == cur){parent->_bf--;}else{parent->_bf++;}if (parent->_bf == 0){break;}else if (parent->_bf == 1 || parent->_bf == -1){//继续向上更新cur = parent;parent = parent->_parent;}else if (parent->_bf == 2 || parent->_bf == -2){//旋转//右单旋if (parent->_bf == -2 && cur->_bf == -1){RotateR(parent);}//左单旋else if (parent->_bf == 2 && cur->_bf == 1){RotateL(parent);}else if (parent->_bf == -2 && cur->_bf == 1){//左右旋RotateLR(parent);}else if (parent->_bf == 2 && cur->_bf == -1){//右左旋RotateRL(parent);}else{assert(false);}break;}else{assert(false);}}return true;}//右旋void RotateR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;Node* Pparent = parent->_parent;if (subLR){subLR->_parent = parent;}subL->_right = parent;parent->_parent = subL;parent->_left = subLR;if (Pparent == nullptr){_root = subL;subL->_parent = nullptr;}else{if (Pparent->_left == parent){Pparent->_left = subL;}else{Pparent->_right = subL;}subL->_parent = Pparent;}parent->_bf = 0;subL->_bf = 0;}//左旋void RotateL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;Node* Pparent = parent->_parent;if (subRL){subRL->_parent = parent;}subR->_left = parent;parent->_parent = subR;parent->_right = subRL;if (Pparent == nullptr){_root = subR;subR->_parent = nullptr;}else{if (Pparent->_left == parent){Pparent->_left = subR;}else{Pparent->_right = subR;}subR->_parent = Pparent;}parent->_bf = 0;subR->_bf = 0;}//左右旋void RotateLR(Node* parent){//subL subLR parentNode* subL = parent->_left;Node* subLR = subL->_right;int bf = subLR->_bf;RotateL(subL);RotateR(parent);if (bf == 0){subL->_bf = 0;subLR->_bf = 0;parent->_bf = 0;}else if (bf == 1){subL->_bf = -1;subLR->_bf = 0;parent->_bf = 0;}else if (bf == -1){subL->_bf = 0;subLR->_bf = 0;parent->_bf = 1;}else{assert(false);}}//右左旋void RotateRL(Node* parent){//parent subRL subRNode* subR = parent->_right;Node* subRL = subR->_left;int bf = subRL->_bf;RotateR(subR);RotateL(parent);if (bf == 0){subR->_bf = 0;subRL->_bf = 0;parent->_bf = 0;}else if (bf == 1){subR->_bf = 0;subRL->_bf = 0;parent->_bf = -1;}else if (bf == -1){subR->_bf = 1;subRL->_bf = 0;parent->_bf = 0;}else{assert(false);}}int Height(){return _Height(_root);}int Size(){return _Size(_root);}bool IsBalanceTree(){return _IsBalanceTree(_root);}void InOrder(){_InOrder(_root);cout << endl;}Node* Find(const K& key){Node* cur = _root;while (cur){if (cur->_kv.first < key){cur = cur->_right;}else if (cur->_kv.first > key){cur = cur->_left;}else{return cur;}}return nullptr;}private://高度int _Height(Node* root){if (root == nullptr){return 0;}int left = _Height(root->_left);int right = _Height(root->_right);return left > right ? left + 1 : right + 1;}//结点个数int _Size(Node* root){if (root == nullptr){return 0;}return _Size(root->_left) + _Size(root->_right) + 1;}//判断bool _IsBalanceTree(Node* root){//空树也是AVL树if (root == nullptr){return true;}int leftHeight = _Height(root->_left);int rightHeight = _Height(root->_right);int diff = rightHeight - leftHeight;if (abs(diff) >= 2){cout << root->_kv.first << "高度差异常" << endl;return false;}if (root->_bf != diff){cout << root->_kv.first << "平衡因子异常" << endl;return false;}return _IsBalanceTree(root->_left) && _IsBalanceTree(root->_right);}//中序遍历void _InOrder(Node* root){if (root == nullptr){return;}_InOrder(root->_left);cout << root->_kv.first << ":" << root->_kv.second << endl;_InOrder(root->_right);}private:Node* _root = nullptr;
};test.cpp
//#include "a.h"
#include "AVL.h"
#include <vector>void test01()
{AVLTree<int, int> t;/*pair<int, int> p(1, 2);cout << p.first << " " << p.second << endl;t.Insert(p);t.Insert({1,1});*/int a[] = { 16, 3, 7, 11, 9, 26, 18, 14, 15 };//int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };for (auto e : a){t.Insert({ e, e });}t.InOrder();cout << t.Size() << endl;cout << t.Height() << endl;cout << t.IsBalanceTree() << endl;
}void test02()
{const int N = 1000000;vector<int> v;v.reserve(N);srand((unsigned)time(0));for (size_t i = 0; i < N; i++){v.push_back((int)(rand() + i));}size_t begin2 = clock();AVLTree<int, int> t;for (auto e : v){t.Insert(make_pair(e, e));}size_t end2 = clock();cout << "Insert:" << end2 - begin2 << endl;cout << t.IsBalanceTree() << endl;cout << "Height:" << t.Height() << endl;cout << "Size:" << t.Size() << endl;size_t begin1 = clock();// 确定在的值/*for (auto e : v){t.Find(e);}*/// 随机值for (size_t i = 0; i < N; i++){t.Find(((int)(rand() + i)));}size_t end1 = clock();cout << "Find:" << end1 - begin1 << endl;
}int main()
{//test01();test02();return 0;
}
相关文章:

C++——AVL树
文章目录 一、AVL树的概念二、AVL树的实现1. AVL树的结构2. AVL树的插⼊2.1 AVL树插⼊⼀个值的⼤概过程2.2 平衡因⼦更新更新原则更新停止条件 2.3 插⼊结点及更新平衡因⼦的代码实现 3. 旋转旋转的原则右单旋左单旋左右双旋右左双旋 4.高度5.结点个数6.判断是否是AVL树7. 中序…...

极市平台 | 无人机相关开源数据集资源汇总
本文来源公众号“极市平台”,仅用于学术分享,侵权删,干货满满。 原文链接:无人机相关开源数据集资源汇总 本文介绍几个无人机有关的开源数据集,内附下载链接。 UAV Delievery 无人机轨迹数据集 下载链接ÿ…...

React和Vue区别,以及注意事项
目录 一、语法和框架特性的差异 二、开发习惯和注意事项 三、特别注意事项 一、语法和框架特性的差异 模板语法: Vue使用了类似于传统HTML的模板语法,通过双大括号{{ }}进行插值,而React则使用了JSX语法。在Vue中,你可以直接在…...

光伏项目难管理的问题如何解决?
1.数字化管理平台的应用 数字化是当前解决光伏项目管理难题的关键手段之一。通过建立统一的数字化管理平台,可以实现对光伏电站的远程监控、数据分析、故障预警及运维调度等功能。这类平台通常集成有智能算法,能够实时分析电站运行数据,及时…...

图片美化SDK解决方案,赋能H5与小程序极致体验
无论是社交媒体分享、电商产品展示,还是个人日常生活的记录,一张经过精心美化的图片总能瞬间吸引眼球,传递出更加丰富和动人的信息。如何在不增加应用体积、不牺牲用户体验的前提下,为H5页面和小程序提供媲美原生APP的图片美化功能…...

Kron Reduction消去法如何操作,矩阵推导过程
三阶矩阵消去单节点 在电力系统中,母线上的电流注入始终为0,这样的节点可以通过一定的方法消除。以三节点为例,假设注入节点3的电流为0,则: [ I 1 I 2 I 3 ] = [ I 1 I 2 0 ] = [ Y 11 Y 12 Y 13 Y 21 Y 22 Y 23 Y 31 Y 32 Y 33 ] [ V 1 V 2 V 3 ] \left[\begin{array}{…...

实时开放词汇目标检测(论文复现)
实时开放词汇目标检测(论文复现) 本文所涉及所有资源均在传知代码平台可获取 文章目录 实时开放词汇目标检测(论文复现)概述模型框架使用方式配置环境训练和评估训练评估 演示效果Gradio Demo 概述 YOLO-World是由腾讯人工智能实验…...

陪诊小程序搭建:打造便利的陪诊环境
陪诊行业作为一个新兴行业,随着老龄化的严重,在近几年中需求量日益旺盛。陪诊师为大众的就医提供了极大的便利性,在看病难、医疗资源紧张方面发挥了积极作用。 在陪诊行业的快速发展下,陪诊小程序为行业带来了便捷的模式…...

Qt5.15.2静态编译 MinGW with static OpenSSL
如果想用VS2017编译,可参考:Qt5.15.2静态编译 VS2017 with static OpenSSL 一.环境 系统:Windows 10 专业版 64位 编译器:MinGW 8.1.0 第三方工具:perl,ruby和python PS:经验证,用MinGW 12.1.0来编译Qt5.15.2会报错 我用Phthon 2.7.18虽然可以编过,但是强烈建议Pyth…...

Linux Ubuntu dbus CAPI ---- #include<dbus.h>出现“无法打开源文件dbus/xxx.h“的问题
一、确保已安装dbus库和CAPI sudo apt-get install libdbus-1-dev 二、在c_cpp_properties.json的includePath中是否配置了dbus库依赖文件所在的路径 三、编译一个简单的dbus代码,在编译过程中只要出现.h文件找不到的情况,就使用下列命令找到.h文件路径…...

React01 开发环境搭建
React 开发环境搭建 一、创建 React 项目二、项目精简 一、创建 React 项目 执行下述命令创建 react 项目 blu-react-basis npx create-react-app blu-react-basis项目目录结构如下: 执行下述命令启动项目 npm run start启动效果如下: 二、项目精简 …...

数据结构之旅(顺序表)
前言: Hello,各位小伙伴们我们在过去的60天里学完了C语言基本语法,由于小编在准备数学竞赛,最近没有给大家更新,并且没有及时回复大家的私信,小编在这里和大家说一声对不起!,小编这几天会及时给大家更新初阶数据结构的内容,然后我们来学习今天的内容吧! 一. 顺序表的概念和结…...

掌握 C# 内存管理与垃圾回收机制
内存管理是每个开发者需要了解的关键部分,特别是在构建高性能应用时。在 C# 中,垃圾回收(Garbage Collection, GC) 机制自动管理内存分配和释放,大大简化了内存管理的复杂性。然而,理解值类型与引用类型的区…...

【JavaEE】——初始网络原理
阿华代码,不是逆风,就是我疯 你们的点赞收藏是我前进最大的动力!! 希望本文内容能够帮助到你!! 目录 一:局域网 1:概念 二:局域网的连接方式 1:网线直连 …...

Nginx和Lua配合使用
在NGINX中使用Lua进行开发时,可以通过不同的配置块来指定Lua脚本的执行位置。这些配置块被称为“phase hooks”,即阶段挂钩。每个阶段挂钩都有其特定的作用时间和目的。以下是NGINX Lua模块中常见的配置指令及其用途: 常见的Phase Hooks 1.a…...

程序化交易是什么,它有哪些优势,需要注意什么?
炒股自动化:申请官方API接口,散户也可以 python炒股自动化(0),申请券商API接口 python炒股自动化(1),量化交易接口区别 Python炒股自动化(2):获取…...

水库抽样算法(大数据算法作业)
时隔一个多月,终于想起来写大数据算法基础的实验报告,主要是快截止了,hh 这两天加急把这个报告写完了~ 接下来,写一写证明过程(参考书籍:高等教育出版社《数据科学与工程算法基础》)主要代码以…...
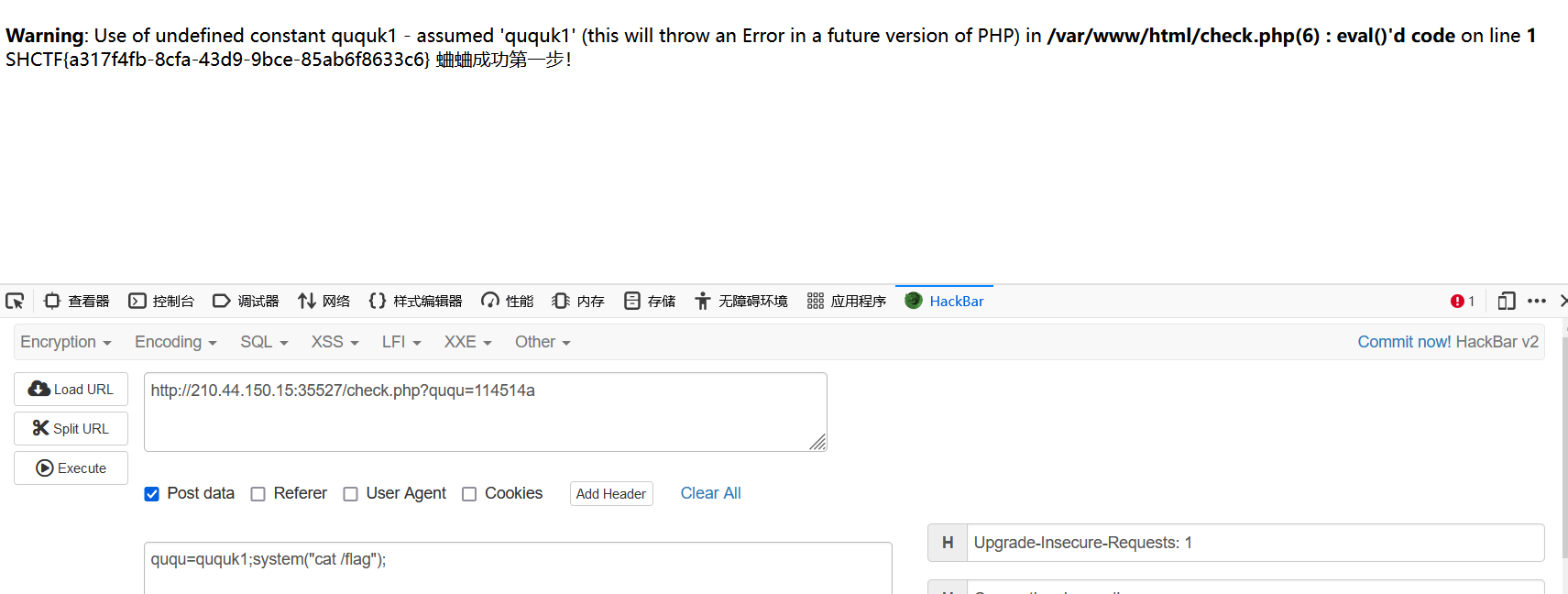
SHCTF-2024-week1-wp
文章目录 SHCTF 2024 week1 wpMisc[Week1]真真假假?遮遮掩掩![Week1]拜师之旅①[Week1]Rasterizing Traffic[Week1]有WiFi干嘛不用呢? web[Week1] 单身十八年的手速[Week1] MD5 Master[Week1] ez_gittt[Week1] jvav[Week1] poppopop[Week1] 蛐蛐?蛐蛐! SHCTF 2024…...

docker-comapose安装部署mysql
docker-comapose安装部署mysql version: "3.4" services:mysql:image: docker.das-security.cn/middleware/mysql:8.4.1container_name: mysqlenvironment:- MYSQL_ROOT_PASSWORD密码volumes:- /etc/localtime:/etc/localtime- ./configs/mysql/initdb:/docker-entr…...

C语言初阶-数据类型和变量【下】
紧接上期------------------------->>>C语言初阶-数据类型和变量【上】 全局变量和局部变量在内存中存储在哪⾥呢? ⼀般我们在学习C/C语⾔的时候,我们会关注内存中的三个区域: 栈区 、 堆区 、 静态区 。 内存的分配情况 局部变量是…...
。】2022-5-15)
【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15
缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下: struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...

ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上,你可以使用apt包管理器来安装NFS服务器。打开终端并运行: sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享,例如/shared: sudo mkdir /shared sud…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...
 自用)
css3笔记 (1) 自用
outline: none 用于移除元素获得焦点时默认的轮廓线 broder:0 用于移除边框 font-size:0 用于设置字体不显示 list-style: none 消除<li> 标签默认样式 margin: xx auto 版心居中 width:100% 通栏 vertical-align 作用于行内元素 / 表格单元格ÿ…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...

MySQL的pymysql操作
本章是MySQL的最后一章,MySQL到此完结,下一站Hadoop!!! 这章很简单,完整代码在最后,详细讲解之前python课程里面也有,感兴趣的可以往前找一下 一、查询操作 我们需要打开pycharm …...

JDK 17 序列化是怎么回事
如何序列化?其实很简单,就是根据每个类型,用工厂类调用。逐个完成。 没什么漂亮的代码,只有有效、稳定的代码。 代码中调用toJson toJson 代码 mapper.writeValueAsString ObjectMapper DefaultSerializerProvider 一堆实…...

P10909 [蓝桥杯 2024 国 B] 立定跳远
# P10909 [蓝桥杯 2024 国 B] 立定跳远 ## 题目描述 在运动会上,小明从数轴的原点开始向正方向立定跳远。项目设置了 $n$ 个检查点 $a_1, a_2, \cdots , a_n$ 且 $a_i \ge a_{i−1} > 0$。小明必须先后跳跃到每个检查点上且只能跳跃到检查点上。同时࿰…...
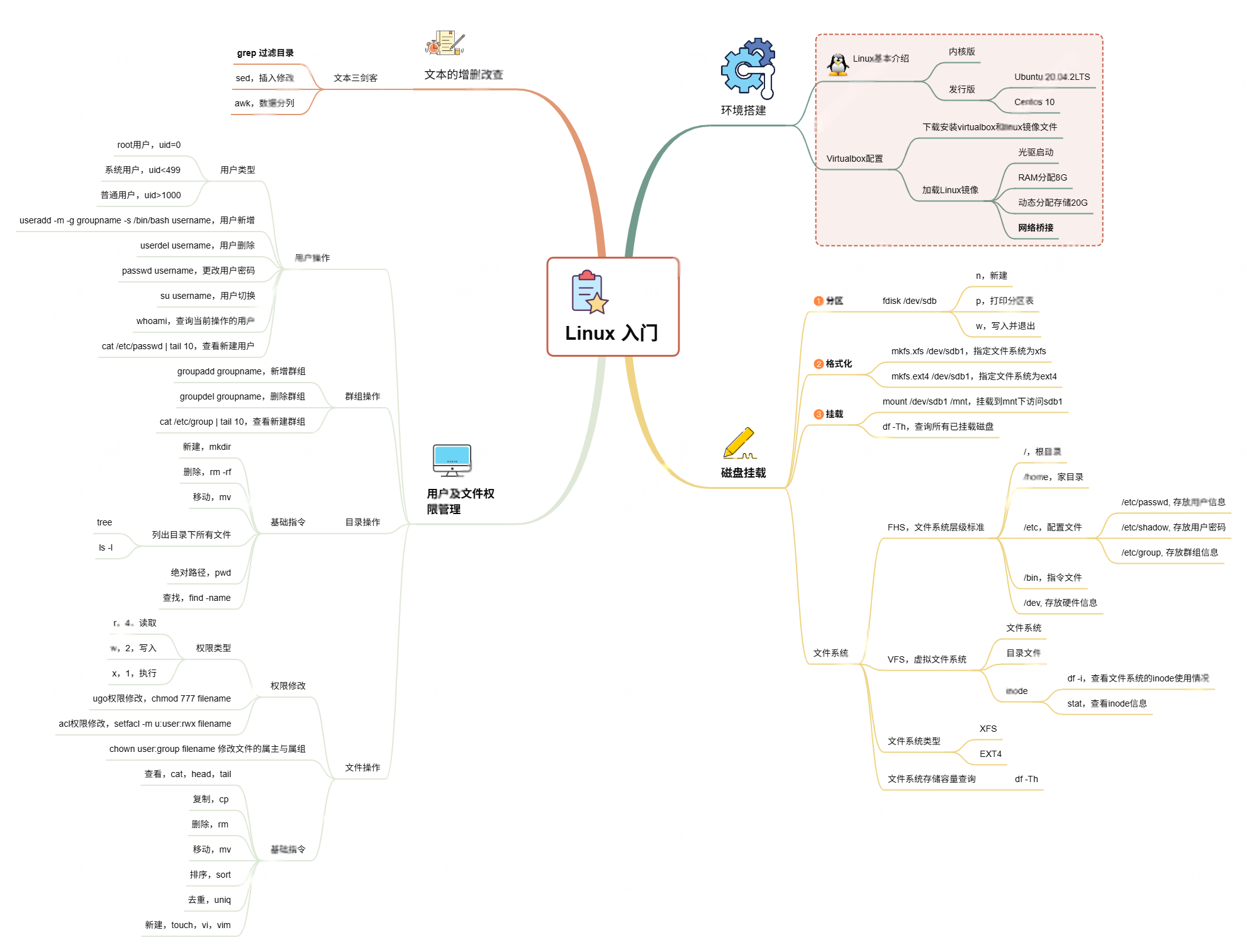
Linux入门课的思维导图
耗时两周,终于把慕课网上的Linux的基础入门课实操、总结完了! 第一次以Blog的形式做学习记录,过程很有意思,但也很耗时。 课程时长5h,涉及到很多专有名词,要去逐个查找,以前接触过的概念因为时…...
