第十五届蓝桥杯C++B组省赛

文章目录
- 1.握手问题
- 解题思路1(组合数学)
- 解题思路2(暴力枚举)
- 2.小球反弹
- 做题思路
- 3.好数
- 算法思路(暴力解法)---不会超时
- 4.R格式
- 算法思路
- 5.宝石组合
- 算法思路---唯一分解定理
- 6.数字接龙
- 算法思路----DFS
- 7.拔河
- 算法思路
1.握手问题
题目描述:

解题思路1(组合数学)
按照题目描述来说,会议有五十人,如果不加任何限制条件,这五十个人两两握手的次数是:
t o t a l = 49 + 48 + 47 + . . . . . . . . + 1 total=49+48+47+........+1 total=49+48+47+........+1
利用高斯求和的得出: t o t a l = 50 ∗ 49 / 2 total=50*49/2 total=50∗49/2
如果加上限制条件的话,题目给定的其中有七个人不会相互握手,需要用上面总的不加限制的减去七个人相互握手的次数。
c n t = 6 + 5 + . . . . . . + 1 = 7 ∗ 6 / 2 cnt=6+5+......+1=7*6/2 cnt=6+5+......+1=7∗6/2
上述两式作差即可
编写代码:
#include<iostream>
using namespace std;
int main()
{int total = 50 * 49 / 2;int cnt = 7 * 6 / 2;cout << total - cnt << endl;return 0;
}
解题思路2(暴力枚举)
将每个人握手的情况枚举出来即可。
#include<iostream>
using namespace std;
int main()
{int ans = 0;for (int i = 1;i <= 50;i++){for (int j = i + 1;j <= 50;j++){//排除掉七人的情况if (!(i >= 1 && i <= 7 && j >= 1 && j <= 7)){ans++;}}}cout << ans << endl;return 0;
}
2.小球反弹
问题描述:

做题思路
这道题我们肯定不能直接做的,这道题给定了 d x : d y dx:dy dx:dy的值说明这道题我们应该分解来做,将小球的反弹的路径分解为x方向和y方向来做。
我们首先假设x方向上经过了p个来回,y方向上经历了q个来回,因为是分解的缘故,所以两个分解方向上的时间是相同的。
所以可以得出两个等式:
d x ∗ t = 2 p x dx*t=2px dx∗t=2px(由于这里一半的路程是x,所以一个来回的路程是2x,乘以来回就是总路程)
d y ∗ t = 2 q x dy*t=2qx dy∗t=2qx
将这两个式子进行比例
d x d y = p x q y \frac{dx}{dy}=\frac{px}{qy} dydx=qypx
得到这个式子之后我们可以利用gcd对这个式子的左边进行约分。
可以得出: p = d x ∗ y p=dx*y p=dx∗y和 q = d y ∗ x q=dy*x q=dy∗x
算出q或者p之后可以利用公式计算t: t = 2 p x / d x t=2px/dx t=2px/dx
最后得出总路程: 总路程 = t ∗ ( s q r t ( 1 5 2 + 1 7 2 ) ) 总路程=t*(sqrt(15^2+17^2)) 总路程=t∗(sqrt(152+172))
编写代码:
//求最大公约数
int gcd(int a, int b)
{return b == 0 ? a : gcd(b, a % b);
}
int main()
{//给出x方向和y方向的速度 int dx = 15, dy = 17;//给出x方向和y方向上的距离int x = 343720, y = 233333;//求出多少来回int q = dy * x, p = dx * y;//求最大公约数int g = gcd(p, q);p /= g, q /= g;//计算时间int t = 2 * p * x / dx;//求路程double ans = t * sqrt(15 * 15 + 17 * 17);printf("%.2lf\n", ans);return 0;
}
3.好数
问题描述:

数据量:

算法思路(暴力解法)—不会超时
遍历1到n的数,然后写一个check函数判断每个数是否是好数,这里的时间复杂度是 n ∗ l o g n n*logn n∗logn
编写代码:
#include <iostream>
using namespace std;
int N,count;bool Check(int n)
{int i=1;while(n!=0){int tail=n%10;if(i%2==1){if(tail%2!=1)return false;}else{if(tail%2!=0)return false;}i++;n/=10;}return true;
}int main()
{// 请在此输入您的代码cin>>N;for(int i=1;i<N;i++){if(Check(i)){count++;}}cout<<count<<endl;return 0;
}
4.R格式
题目描述:

数据量:

可以看到这道题的数据量是很大的,涉及到了幂次,肯定不可能直接去算,这道题很显然是考察的是高精度算法(高精度*低精度)
算法思路
高精度模版题:
编写代码:
#include<iostream>
#include<algorithm>
#include<string>
#include<cmath>
using namespace std;//数组模拟高精度:高精度*低精度
const int N = 2e3 + 10;
string s;
int a[N];
int main()
{int n;cin >> n >> s;//反转操作reverse(s.begin(), s.end());//确定小数点的位置int pos = s.find(".");s.erase(pos, 1);//删除小数点,方便后续计算int len = s.size();for (int i = 0;i < len;i++) a[i + 1] = s[i] - '0';//高精度*低精度for (int i = 1;i <= n;i++){//顺序扫描,均*2for (int j = 1;j <= len;j++) a[j] *= 2;//处理大于10的位数for (int j = 1;j <= len;j++){if (a[j] >= 10){a[j + 1]++;a[j] %= 10;if (j == len) len++;}}}//处理小数点后的第一位,进行四舍五入if (a[pos] >= 5)a[pos + 1]++;for (int i = pos + 1;i <= len;i++){if (a[i] >= 10){a[i + 1]++;a[i] %= 10;if (i == len)len++;}}//打印的时候倒序打印for (int i = len;i >= pos + 1;i--) cout << a[i];return 0;
}
5.宝石组合
题目描述:

数据范围:

首先从数据量来看这道题是不能用暴力枚举的,因为暴力枚举三个数的时间复杂度是 O ( N 3 ) O(N^3) O(N3)了。
算法思路—唯一分解定理
首先我们要知道什么是唯一分解定理,简单来说唯一分解定理就是,任意一个大于1的正整数 ,都可以唯一地表示为若干个质数的乘积,且这些质数的顺序不影响分解的唯一性。
那么可以得出:
N 1 = p 1 a 1 ⋅ p 2 a 2 ⋅ … ⋅ p n a n N_1 = p_1^{a_1} \cdot p_2^{a_2} \cdot \ldots \cdot p_n^{a_n} N1=p1a1⋅p2a2⋅…⋅pnan
N 2 = p 1 b 1 ⋅ p 2 b 2 ⋅ … ⋅ p n b n N_2 = p_1^{b_1} \cdot p_2^{b_2} \cdot \ldots \cdot p_n^{b_n} N2=p1b1⋅p2b2⋅…⋅pnbn
从上面两个式子可以得出:
gcd ( N 1 , N 2 ) = p 1 min ( a 1 , b 1 ) ⋅ p 2 min ( a 2 , b 2 ) ⋅ … ⋅ p n min ( a n , b n ) \gcd(N_1,N_2) = p_1^{\min(a_1,b_1)} \cdot p_2^{\min(a_2,b_2)} \cdot \ldots \cdot p_n^{\min(a_n,b_n)} gcd(N1,N2)=p1min(a1,b1)⋅p2min(a2,b2)⋅…⋅pnmin(an,bn)
lcm ( N 1 , N 2 ) = p 1 max ( a 1 , b 1 ) ⋅ p 2 max ( a 2 , b 2 ) ⋅ … ⋅ p n max ( a n , b n ) \operatorname{lcm}(N_1,N_2) = p_1^{\max(a_1,b_1)} \cdot p_2^{\max(a_2,b_2)} \cdot \ldots \cdot p_n^{\max(a_n,b_n)} lcm(N1,N2)=p1max(a1,b1)⋅p2max(a2,b2)⋅…⋅pnmax(an,bn)
假设Ha,Hb,Hc的分解出来的相同的质数的幂次分别是x,y,z那么可以得出:

上面的式子可以转换为幂次是:
x + y + z + max ( x , y , z ) − max ( x , y ) − max ( x , z ) − max ( y , z ) x+y+z+\max(x,y,z)-\max(x,y)-\max(x,z)-\max(y,z) x+y+z+max(x,y,z)−max(x,y)−max(x,z)−max(y,z)
相当于我们只需要求出上面式子的最大值即可。
编写代码:
#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
const int N = 1e5 + 10;
int a[N];
//fac是存储因子的二维数组,s是求的最大值
vector<int> fac[N], s[N];
int main()
{//遍历数组for (int i = 1;i <= 1e5;i++){for (int j = i;j <= 1e5;j += i){//i是j的因子fac[j].push_back(i);}}//输入n个数int n;cin >> n;for (int i = 1;i <= n;i++)cin >> a[i];//保证字典序最小sort(a + 1, a + n + 1);for (int i = 1;i <= n;i++){//处理i的每个因子for (int j = 0;j < fac[a[i]].size();j++){//s[fac[a[i]][j]].push_back(a[i]);}}for (int i = 1e5;i >= 0;i--){if (s[i].size() >= 3){cout << s[i][0] << ' ' << s[i][1] << ' ' << s[i][2] << endl;break;}}return 0;
}
6.数字接龙
问题描述:


数据量:

根据数据量来看这道题考察的应该是DFS,但是在DFS中应该还涉及到回溯,因为当走到不满足条件的时候需要进行回溯。
算法思路----DFS
编写代码:
#include<iostream>
#include<string>
using namespace std;
const int N = 20;
int a[N][N];
bool vis[N][N];
int n, k;
//方向数组: 0 1 2 3 4 5 6 7
int dx[8] = { -1,-1,0,1,1,1,0,-1 };
int dy[8] = { 0,1,1,1,0,-1,-1,-1 };
string res;void dfs(int x, int y, int prev, string s, int dep)
{//当搜到终点的时候,且搜索深度是n的时候,意思就是每种情况都搜索完了if (x == n && y == n && dep == n * n) {if (res.empty())res = s;return;}for (int i = 0;i < 8;i++){//生成邻接点int bx = x + dx[i];int by = y + dy[i];//过滤越界节点if (bx<1 || bx>n || by<1 || by>n)continue;//过滤访问过的节点if (vis[bx][by] == true)continue;//防止交叉搜索if (i == 1 && vis[x - 1][y] && vis[x][y + 1])continue;if (i == 3 && vis[x + 1][y] && vis[x][y + 1])continue;if (i == 5 && vis[x + 1][y] && vis[x][y - 1])continue;if (i == 7 && vis[x - 1][y] && vis[x][y - 1])continue;//保证路径数值为0 1 2 3 .....k-1if ((a[bx][by] < k && a[bx][by] == prev + 1) || (prev + 1 == k && a[bx][by] == 0)){//可以搜索,将点标记为truevis[bx][by] = true;dfs(bx, by, a[bx][by], s + to_string(i), dep + 1);//最优性剪枝if (!res.empty())return;vis[bx][by] = false;//回溯}}
}int main()
{cin >> n >> k;for (int i = 1;i <= n;i++)for (int j = 1;j <= n;j++)cin >> a[i][j];string emp;//标记起点vis[1][1] = true;dfs(1, 1, 0, emp, 1);if (res.empty())cout << -1;else cout << res << endl;return 0;
}
7.拔河
问题描述:

数据量:

对于这种涉及到区间和的题来说,大概率都是用前缀和算法解决
算法思路
编写代码:
#include<iostream>
#include<set>
#include<climits>
using namespace std;#define ll long longconst int N = 1e3 + 10;
int a[N], s[N];//前缀和和数组
multiset<int> ms;int main()
{int n;cin >> n;for (int i = 1;i <= n;i++){cin >> a[i];//前缀和s[i] = s[i - 1] + a[i];}//用set去维护所有的区间和for (int i = 1;i <= n;i++){for (int j = 1;j <= n;j++){//维护区间和ms.insert(s[j] - s[i - 1]);}}int ans = LONG_MAX;for (int i = 1;i <= n;i++){for (int j = 1;j < i;j++){//枚举以i结尾的区间,因为这里i-1只会有一个人,所以应该是j-1int sum = s[i] - s[j - 1];//找到与该区间和sum相似的区间和auto it = ms.lower_bound(sum);if (it != ms.end()){ans = min(ans, abs(*it - sum));}if (it != ms.begin()){it--;ans = min(ans, abs(*it - sum));}}//删除以i开头且以j结尾的区间,防止后续查询区间的时候出现区间重叠/交叉问题for (int j = i;j <= n;j++) ms.erase(ms.find(s[j] - s[i - 1]));}cout << ans << endl;return 0;
}
相关文章:

第十五届蓝桥杯C++B组省赛
文章目录 1.握手问题解题思路1(组合数学)解题思路2(暴力枚举) 2.小球反弹做题思路 3.好数算法思路(暴力解法)---不会超时 4.R格式算法思路 5.宝石组合算法思路---唯一分解定理 6.数字接龙算法思路----DFS 7…...

线程 vs 虚拟线程:深入理解及区别
Java 提供了两种线程机制:普通线程(平台线程)和 虚拟线程。普通线程是 Java 中经典的并发处理方式,而虚拟线程是随着 Java 21 引入的新特性,旨在提升并发性能和开发体验。本文将详细探讨它们的区别,并帮助你…...

【WEB应用安全测试指南–蓝队安全测试2】--超详细-可直接进行实战!!!亲测-可进行安全及渗透测试
安全基础理论入门知识参考上一篇《WEB应用安全测试指南蓝队安全测试1》 WEB应用安全测试指南2 一、文件 I/O 类1.1、任意文件上传1.2、任意文件下载1.3、文件包含 二、接口安全类2.1、短信炸弹2.2、邮件炸弹2.3、短信内容可控2.4、邮件内容可控 三、逻辑流程类3.1、越权3.2、未…...

使用HTML、CSS和JavaScript创建滚动弹幕效果
使用HTML、CSS和JavaScript创建滚动弹幕效果 在现代网页设计中,滚动文本是一种常见的动态效果,可以吸引用户的注意力并增强交互体验。在这篇博客文章中,我们将详细介绍如何使用HTML、CSS和JavaScript实现滚动文本效果。 效果 步骤1…...

【C语言】--数组
😊个人主页: 起名字真南 😋个人专栏:【数据结构初阶】 【C语言】 【C】 目录 1 数组的概念2 一维数组的创建和初始化2.2 数组的初始化2.3 数组类型 3 一维数组的使用3.1 数组下标3.2 数组的输入 4 一维数组在内存中的存储5 sizeof计算数组中的元素6 二维…...

面向B2B市场的Spring Boot医疗病历系统开发
第1章绪论 计算机已经从科研院所,大中型企业,走进了平常百姓家,Internet遍及世界各地,在网上能够用计算机进行文字草拟、修改、打印清样、文件登陆、检索、综合统计、分类、数据库管理等,用科学的方法将无序的信息进行…...
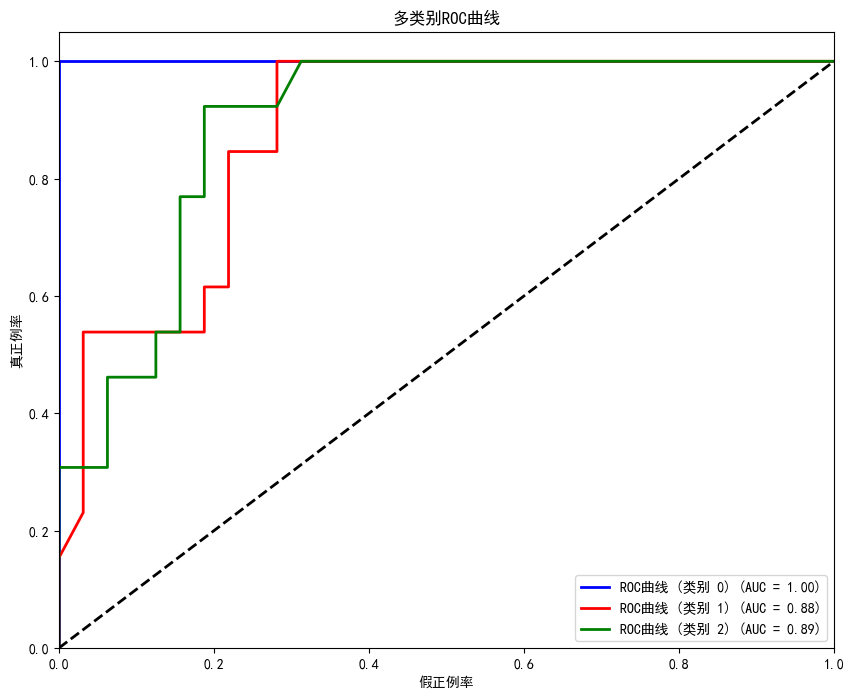
闭着眼学机器学习——支持向量机分类
引言: 在正文开始之前,首先给大家介绍一个不错的人工智能学习教程:https://www.captainbed.cn/bbs。其中包含了机器学习、深度学习、强化学习等系列教程,感兴趣的读者可以自行查阅。 1. 算法介绍 支持向量机(Support Vector Mach…...

今日指数项目day8实战权限管理器(上)
3.权限管理器 3.1 权限列表展示功能 1)原型效果 2)接口说明 功能描述: 查询所有权限集合 服务路径: /api/permissions 服务方法:Get 请求参数:无响应数据格式: {"code": 1,"data":…...
《机器学习与数据挖掘综合实践》实训课程教学解决方案
一、引言 随着信息技术的飞速发展,人工智能已成为推动社会进步的重要力量。作为人工智能的核心技术之一,机器学习与数据挖掘在各行各业的应用日益广泛。本方案旨在通过系统的理论教学、丰富的实践案例和先进的实训平台,帮助学生掌握机器学习…...

linux中软连接和硬链接的区别
定义与概念 硬链接(Hard Link):硬链接是文件系统中的一个概念,它直接指向文件系统中的物理数据块。可以把硬链接看作是原始文件的一个别名,它们共享相同的inode(索引节点)编号。在Linux文件系统…...

#Swift 对比 Static 在Swift 和 OC中的用法
在 Objective-C 和 Swift 中,static 关键字都用于定义类型级别的成员,但它们的用法和行为在两个语言中有所不同。让我们来详细对比一下 Objective-C 和 Swift 中 static 的使用方式和特性。 1. Objective-C 中的 static 在 Objective-C 中,…...

yakit使用教程(三,端口探测和指纹扫描)
本文仅作为学习参考使用,本文作者对任何使用本文进行渗透攻击破坏不负任何责任。 前言: 前文链接:yakit下载安装教程。 1.端口扫描的作用。 对目标端口进行扫描可以知道目标服务器开启了什么服务,以便于针对其所存在的服务展开…...

一维数组的引用
#define SIZE 5 int main(void) { int i 0; int arr[SIZE] { 86,85,85,896,45 };//同理五个数据只是偶然,可能会更多 //输入 for (i 0;i < SIZE;i) { printf("请输入你的第%d个值:",i1); scanf_s(&…...

Vue3 watch 监视属性
作用:监视数据的变化(和Vue2中的watch作用一致)特点:Vue3中的watch只能监视以下四种数据: ref定义的数据。reactive定义的数据。函数返回一个值(getter函数)。一个包含上述内容的数组。 我们在V…...

大数据-158 Apache Kylin 安装配置详解 集群模式启动
点一下关注吧!!!非常感谢!!持续更新!!! 目前已经更新到了: Hadoop(已更完)HDFS(已更完)MapReduce(已更完&am…...
PHP商会招商项目系统一站式服务助力企业腾飞
商会招商项目系统——一站式服务,助力企业腾飞 🚀💼 🚀 开篇:企业成长的加速器,商会招商项目系统来袭 在竞争激烈的市场环境中,企业如何快速找到适合自己的发展路径,实现腾飞&…...

pnpm 和 npm
pnpm 和 npm 是 JavaScript 生态系统中常用的包管理工具,它们各自有不同的特性和优缺点。下面是这两者的详细比较: 1. 基本概念 npm (Node Package Manager): 是 Node.js 的默认包管理器,提供安装、更新、卸载 JavaScript 包的功…...

笔试算法总结
文章目录 题目1题目2题目3题目4 题目1 使用 StringBuilder 模拟栈的行为,通过判断相邻2个字符是否相同,如果相同就进行删除 public class Main {public static String fun(String s) {if (s null || s.length() < 1) return s;StringBuilder builde…...

mybatisPlus对于pgSQL中UUID和UUID[]类型的交互
在PGSQL中,有的类型是UUID和UUID[]这种类型,在mybatis和这些类型交互的时候需要手动设置类型处理器才可以,这里记录一下类型处理器的设置 /*** UUID类型处理器*/ public class UUIDTypeHandler extends BaseTypeHandler<UUID> {/*** 获…...

vue3 高德地图标注(飞线,呼吸点)效果
装下这两个 npm 忘了具体命令了,百度一下就行 “loca”: “^1.0.1”, “amap/amap-jsapi-loader”: “^1.0.1”, <template><div id"map" style"width: 100%;height: 100%;"></div> </template><script setup> …...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

Linux系统部署KES
1、安装准备 1.版本说明V008R006C009B0014 V008:是version产品的大版本。 R006:是release产品特性版本。 C009:是通用版 B0014:是build开发过程中的构建版本2.硬件要求 #安全版和企业版 内存:1GB 以上 硬盘…...

实战三:开发网页端界面完成黑白视频转为彩色视频
一、需求描述 设计一个简单的视频上色应用,用户可以通过网页界面上传黑白视频,系统会自动将其转换为彩色视频。整个过程对用户来说非常简单直观,不需要了解技术细节。 效果图 二、实现思路 总体思路: 用户通过Gradio界面上…...
