【动态规划】子数组系列（下）

1. 等差数列划分

413. 等差数列划分

状态表示：以 i 位置为结尾时的等差数列的个数

状态转移方程：由于至少需要三个元素才符合题目中等差数列的要求，所以需要判断 i - 2，i - 1，i 三个元素，当这三个元素符合等差数列时，那么以 i - 1 为结尾的等差数列再加上 i 也是等差数列，等差数列的个数就 + 1，如果说这三个元素不符合等差数列，那么以 i 为结尾的等差数列个数就是 0

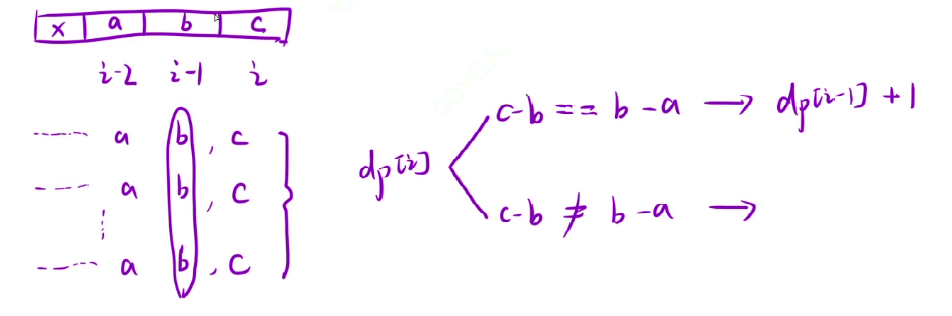
初始化：由于三个元素才能进行等差数列的判断，所以 dp[0]，dp[1] 初始化为 0

返回值：如果数组长度小于 3 直接返回 0，大于等于 3 就返回 dp 数组的和

class Solution {public int numberOfArithmeticSlices(int[] nums) {int n = nums.length;int[] dp = new int[n];int ret = 0;if(n < 3) return 0;for(int i = 2;i < n;i++){dp[i] = (nums[i] - nums[i - 1]) == (nums[i - 1] - nums[i - 2]) ? dp[i - 1] + 1:0; ret += dp[i];}return ret;}
}

2. 最长湍流子数组

978. 最长湍流子数组

状态表示：先用 dp[i] 来表示以第 i 个位置为结尾时的最长湍流数组的长度

f[i]：表示以第 i 个位置为结尾时表示上升状态的最长湍流数组的长度

f[i]：表示以第 i 个位置为结尾时表示下降状态的最长湍流数组的长度

状态转移方程：

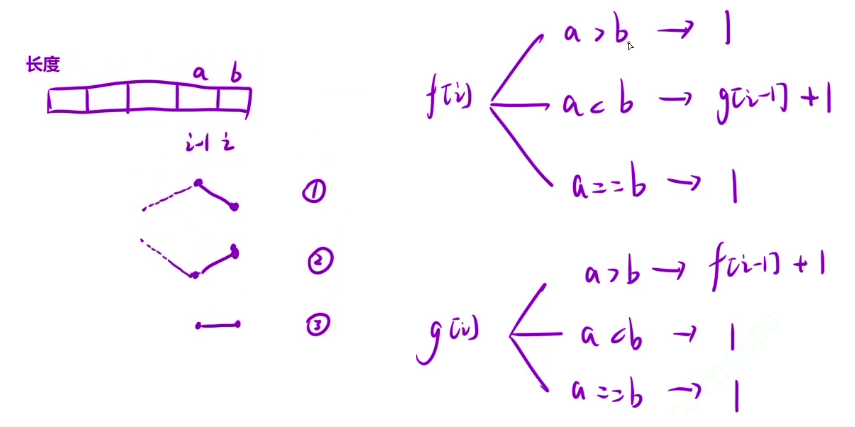
第 i - 1 和 i 位置的状态可能会有下降，上升，相等三种状态，所以定义一个 dp 状态就不够了，需要定义一个上升状态和一个下降状态，当 i - 1 到 i 处于下降状态时，之前应该是处于上升状态的，也就是 f[i - 1]，再加上 1 就是以第 i 个位置为结尾时处于下降状态的最长数组长度，上升也是一样的道理，需要在第 i - 1 位置处于下降状态，就是 g[i - 1] + 1，相等时等于 1 即可

初始化：由于 1 个元素也可以称为湍急子数组，所以可以把 0 下标初始化为 1，又因为状态转移方程中的其他情况是 1 ，为了方便，可以把初始的两个 dp 表都初始化为 1

填表顺序：从左到右

返回值：下降和上升状态的最大值

class Solution {public int maxTurbulenceSize(int[] arr) {int n = arr.length;int[] f = new int[n];int[] g = new int[n];for(int i = 0;i < n;i++){f[i] = g[i] = 1;}int ret = 1;for(int i = 1;i < n;i++){if(arr[i] > arr[i - 1]){g[i] = f[i - 1] + 1;}else if(arr[i] < arr[i - 1]){f[i] = g[i - 1] + 1;}ret = Math.max(Math.max(ret,g[i]),f[i]);}return ret;}
}

3. 单词拆分

139. 单词拆分

状态表示：dp[i] 表示以 i 为结尾时，区间 [0 , i] 之间内能否被字典中的单词拼接而成

状态转移方程：

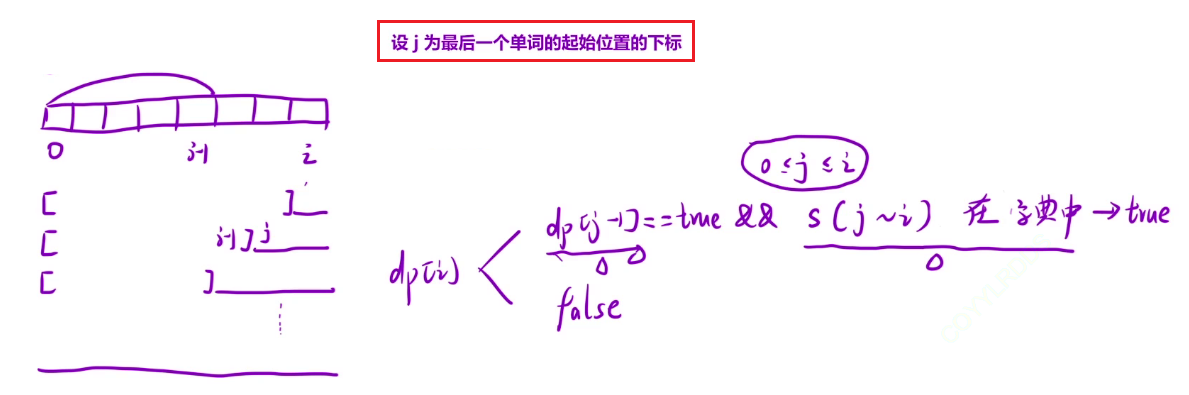
可以把区间分为两段，设 j 为最后一个单词的起始位置的下标，如果 [0 , j - 1] 区间内能够被字典中的单词拼接而成，也就是 dp[j - 1]，再加上 j ~ i 区间的单词在数组中，那么就说明 0 ~ i 区间可以被字典中的单词拼接而成

初始化：为了方便表示 ,dp 数组还是开 n + 1（n 为所给字符串的长度），此时 dp[0] 需要设置为 true 才能不影响后续的判断，如果是 false 的话，那么后面区间就一直都不可以被拼接，dp 数组长度 + 1 之后，为了更方便的表示下标的映射关系，可以把原来的字符串 s 最前面加一个长度为 1 的占位符，这样字符串的下标也对应着 dp 表的下标

填表顺序：从左到右

返回值：dp[n]

为了便于查找 j ~ i 的字符串是否在字典中，可以把题中的字典映射到哈希表中

class Solution {public boolean wordBreak(String s, List<String> wordDict) {int n = s.length();boolean[] dp = new boolean[n + 1];dp[0] = true;s = " " + s;Set<String> hash = new HashSet(wordDict);for(int i = 1;i <= n;i++){//字符串长度 + 1，对应的 j 最小就是 1 下标for(int j = i;j >= 1;j--){//substring 前闭后开 ，所以 i + 1if(dp[j - 1] && hash.contains(s.substring(j,i + 1))){dp[i] = true;//如果找到一种再往前就不用找了break;}}   }return dp[n];}
}

4. 环绕字符串中唯一的子字符串

467. 环绕字符串中唯一的子字符串

状态表示：dp[i] 表示以 i 位置为结尾时，有多少子串出现

状态转移方程：

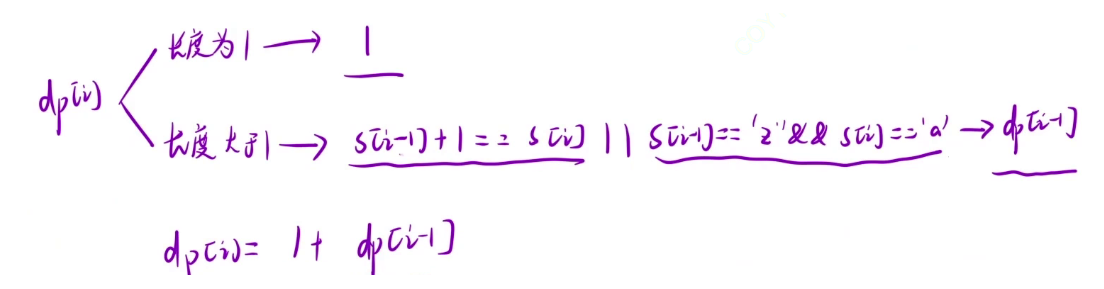
和上一题其实差不多，可以分为长度为 1 和长度大于 1 的，只需要判断是否是连续的，前一个是“z”后一个是 "a" 也算是连续的

初始化：由于长度为 1 时可以算出现一次，长度大于 1 就是找到以 i - 1 为结尾的子串再加上 s[i] ，整体的数量还是 dp[i - 1]，dp[i] 就是把长度为 1 和长度大于 1 的两种情况加起来，所以可以把整个 dp 表初始化为 1 ，然后就只需要判断长度大于 1 时的情况直接相加就行

填表顺序：从左到右

返回值：由于 dp[i] 中存储的是以 i 为结尾时的子串出现的次数，这就可能出现多次，例如“cac”

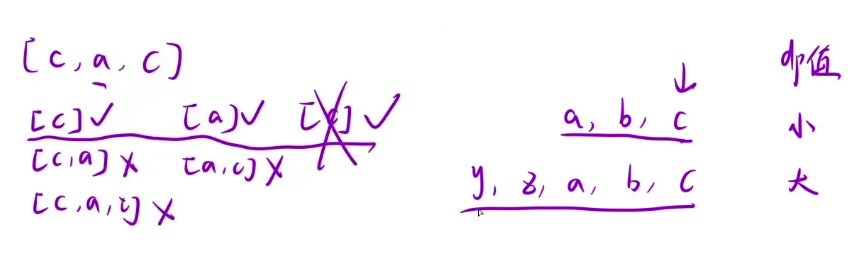
相同的子串只能统计一次，并且可以发现，以同一个字符结尾的子串只需要统计最长的即可，短的情况就包含在了长的情况，所以可以额外定义一个 hash 表来存储最终的答案，最后只需返回 hash 表中的所有和即可

class Solution {public int findSubstringInWraproundString(String s) {int n = s.length();int[] dp = new int[n];Arrays.fill(dp, 1);//表示 26 个字母int[] hash = new int[26];char[] chars = s.toCharArray();for(int i = 1;i < n;i++){if((chars[i] == (chars[i - 1] + 1)) || (chars[i] == 'a'&&chars[i - 1] == 'z')){dp[i] += dp[i - 1];}}int ret = 0;for(int i = 0;i < n;i++){//更新为以当前字符为结尾最长子串的数量hash[chars[i] - 'a'] = Math.max(hash[chars[i] - 'a'],dp[i]);}for(int x : hash) ret += x;return ret;}
}