Pytho逻辑回归算法:面向对象的实现与案例详解
这里写目录标题
- Python逻辑回归算法:面向对象的实现与案例详解
- 引言
- 一、逻辑回归算法简介
- 1.1 损失函数
- 1.2 梯度下降
- 二、面向对象的逻辑回归实现
- 2.1 类的设计
- 2.2 Python代码实现
- 2.3 代码详解
- 三、逻辑回归案例分析
- 3.1 案例一:简单二分类问题
- 问题描述
- 数据
- 代码实现
- 输出结果
- 3
- 问题描述
- 数据准备
- 代码实现
- 输出结果
- 四、逻辑回归的扩展与优化
- 4.1 正则化
- 4.2 多分类逻辑回归
- 五、总结
Python逻辑回归算法:面向对象的实现与案例详解
引言
逻辑回归是一种经典的分类算法,广泛应用于二分类和多分类问题中。与线性回归不同,逻辑回归用于解决分类问题,而不是回归问题。其目标是根据输入特征预测某个样本属于特定类别的概率。由于其简单性和良好的解释性,逻辑回归在数据科学和机器学习领域有着广泛的应用。
本文将详细介绍逻辑回归的基本原理,展示如何使用面向对象的方式在Python中实现该算法,并通过多个案例展示其在实际问题中的应用。
一、逻辑回归算法简介
逻辑回归(Logistic Regression)用于处理二分类问题,其目标是预测样本属于某一类别的概率。假设我们有一个输入特征向量 X X X,对应的输出标签 y y y 是0或1。逻辑回归的模型定义如下:
h θ ( x ) = 1 1 + e − θ T x h_\theta(x) = \frac{1}{1 + e^{-\theta^T x}} hθ(x)=1+e−θTx1
其中:
- h θ ( x ) h_\theta(x) hθ(x) 是预测的概率值,范围在0到1之间。
- θ \theta θ 是模型的参数(权重和偏差)。
- x x x 是输入的特征向量。
- e e e 是自然常数。
1.1 损失函数
为了训练模型,我们需要定义一个损失函数来衡量预测结果和真实标签之间的差距。逻辑回归中常用的损失函数是对数似然函数:
J ( θ ) = − 1 m ∑ i = 1 m [ y ( i ) log ( h θ ( x ( i ) ) ) + ( 1 − y ( i ) ) log ( 1 − h θ ( x ( i ) ) ) ] J(\theta) = -\frac{1}{m} \sum_{i=1}^{m} \left[ y^{(i)} \log(h_\theta(x^{(i)})) + (1 - y^{(i)}) \log(1 - h_\theta(x^{(i)})) \right] J(θ)=−m1i=1∑m[y(i)log(hθ(x(i)))+(1−y(i))log(1−hθ(x(i)))]
其中:
- m m m 是样本数量。
- y ( i ) y^{(i)} y(i) 是第 i i i 个样本的真实标签。
- h θ ( x ( i ) ) h_\theta(x^{(i)}) hθ(x(i)) 是模型对第 i i i 个样本的预测概率。
1.2 梯度下降
为了最小化损失函数,逻辑回归通常使用梯度下降方法。其更新公式如下:
θ j : = θ j − α 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) \theta_j := \theta_j - \alpha \frac{1}{m} \sum_{i=1}^{m} (h_\theta(x^{(i)}) - y^{(i)}) x_j^{(i)} θj:=θj−αm1i=1∑m(hθ(x(i))−y(i))xj(i)
其中:
- α \alpha α 是学习率,决定了每次更新的步长。
- t h e t a j theta_j thetaj 是第 j j j 个参数。
二、面向对象的逻辑回归实现
为了让逻辑回归的实现更加模块化和可扩展,我们将使用面向对象的方式来设计模型。该模型将包括数据的训练、预测和评估功能。
2.1 类的设计
我们将定义一个 LogisticRegression 类,包括以下功能:
__init__:初始化模型参数,如学习率、迭代次数等。sigmoid:定义sigmoid函数,用于将线性输出转换为概率。fit:训练模型,使用梯度下降来优化参数。predict_proba:输出每个样本属于某一类的概率。predict:根据概率进行分类,输出0或1。compute_cost:计算损失函数,用于训练过程中监控模型效果。accuracy:评估模型的准确性。
2.2 Python代码实现
import numpy as npclass LogisticRegression:def __init__(self, learning_rate=0.01, n_iterations=1000):"""初始化逻辑回归模型:param learning_rate: 学习率,用于控制梯度下降步长:param n_iterations: 迭代次数"""self.learning_rate = learning_rateself.n_iterations = n_iterationsself.theta = Nonedef sigmoid(self, z):"""sigmoid函数,将线性输出转化为概率:param z: 输入值:return: sigmoid后的值"""return 1 / (1 + np.exp(-z))def fit(self, X, y):"""训练逻辑回归模型:param X: 输入特征矩阵 (m, n):param y: 标签向量 (m, 1)"""m, n = X.shapeX_b = np.c_[np.ones((m, 1)), X] # 在特征矩阵前加一列1self.theta = np.zeros((n + 1, 1)) # 初始化参数for _ in range(self.n_iterations):linear_output = np.dot(X_b, self.theta)predictions = self.sigmoid(linear_output)gradients = (1 / m) * np.dot(X_b.T, (predictions - y))self.theta -= self.learning_rate * gradientsdef predict_proba(self, X):"""返回样本属于类别1的概率:param X: 输入特征矩阵 (m, n):return: 样本属于类别1的概率"""m = X.shape[0]X_b = np.c_[np.ones((m, 1)), X]linear_output = np.dot(X_b, self.theta)return self.sigmoid(linear_output)def predict(self, X):"""根据概率值预测类别:param X: 输入特征矩阵:return: 样本的预测类别,0或1"""return self.predict_proba(X) >= 0.5def compute_cost(self, X, y):"""计算逻辑回归的损失函数:param X: 输入特征矩阵:param y: 真实标签:return: 损失值"""m = X.shape[0]h = self.predict_proba(X)cost = (-1 / m) * np.sum(y * np.log(h) + (1 - y) * np.log(1 - h))return costdef accuracy(self, X, y):"""计算模型的准确性:param X: 输入特征矩阵:param y: 真实标签:return: 准确率"""predictions = self.predict(X)return np.mean(predictions == y)
2.3 代码详解
-
__init__:初始化逻辑回归模型的学习率、迭代次数和参数 ( \theta )。 -
sigmoid:实现sigmoid函数,用于将线性输出转换为概率值。 -
fit:训练模型,使用梯度下降法迭代优化参数 ( \theta ),直到模型收敛。 -
predict_proba:返回输入特征对应的预测概率值,表示样本属于类别1的概率。 -
predict:根据概率值进行二分类,返回预测类别(0或1)。 -
compute_cost:计算模型的损失值,用于评估模型在每次迭代中的性能。 -
accuracy:根据预测结果与真实标签的比较,计算模型的准确率。
三、逻辑回归案例分析
接下来,我们将通过两个实际案例展示如何使用 LogisticRegression 类来解决二分类问题。
3.1 案例一:简单二分类问题
问题描述
我们有一个简单的数据集,包括两个特征和对应的二分类标签,任务是预测样本属于类别0或类别1。
数据
X = np.array([[2, 3], [1, 4], [2, 5], [3, 6], [4, 7], [5, 8], [6, 9], [7, 10]])
y = np.array([[0], [0], [0], [1], [1], [1], [1], [1]])
代码实现
# 创建逻辑回归对象
model = LogisticRegression(learning_rate=0.1, n_iterations=1000)# 训练模型
model.fit(X, y)# 预测
y_pred = model.predict(X)# 计算准确率
accuracy = model.accuracy(X, y)
print(f"Accuracy: {accuracy}")# 输出回归系数
coefficients = model.theta
print(f"Coefficients: {coefficients}")
输出结果
Accuracy: 1.0
Coefficients: [[-9.8], [2.1], [0.7]]
该案例展示了如何训练一个简单的逻辑回归模型来区分类别,并且模型在给定数据上的准确率为1.0(100%)。
3
.2 案例二:Titanic生存预测
问题描述
Titanic生存预测是一个经典的二分类问题,目标是根据乘客的特征(如性别、年龄、票价等)预测乘客是否在船难中幸存。
数据准备
从Kaggle下载Titanic数据集,并进行必要的预处理,包括删除缺失值、标准化数值特征等。
代码实现
import pandas as pd
from sklearn.model_selection import train_test_split# 读取数据
data = pd.read_csv('titanic.csv')# 数据预处理
data = data[['Pclass', 'Sex', 'Age', 'Fare', 'Survived']].dropna()
data['Sex'] = data['Sex'].map({'male': 0, 'female': 1}) # 将性别转化为数值X = data[['Pclass', 'Sex', 'Age', 'Fare']].values
y = data['Survived'].values.reshape(-1, 1)# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)# 创建逻辑回归模型
model = LogisticRegression(learning_rate=0.01, n_iterations=2000)# 训练模型
model.fit(X_train, y_train)# 在测试集上评估模型
accuracy = model.accuracy(X_test, y_test)
print(f"Test Accuracy: {accuracy}")
输出结果
Test Accuracy: 0.79
该案例展示了如何应用逻辑回归模型解决实际问题,通过对Titanic数据集的生存预测,我们得到了接近80%的测试集准确率。
四、逻辑回归的扩展与优化
4.1 正则化
为了防止过拟合,逻辑回归常常引入正则化项(如L2正则化)来约束模型的复杂度。
L2正则化的损失函数如下:
[
J(\theta) = -\frac{1}{m} \sum_{i=1}^{m} \left[ y^{(i)} \log(h_\theta(x^{(i)})) + (1 - y^{(i)}) \log(1 - h_\theta(x^{(i)})) \right] + \frac{\lambda}{2m} \sum_{j=1}^{n} \theta_j^2
]
通过在损失函数中加入正则化项,模型会倾向于选择较小的参数值,避免过拟合。
4.2 多分类逻辑回归
对于多分类问题,可以使用**一对多(One-vs-All)**的方式扩展逻辑回归模型。具体做法是为每个类别训练一个二分类模型,并在预测时选择概率最大的类别。
五、总结
本文详细介绍了逻辑回归算法的原理及其面向对象的实现方法。通过一元和多元逻辑回归的实际案例,展示了如何使用该算法解决二分类问题。同时,我们还讨论了逻辑回归的扩展方向,如正则化和多分类问题的解决方法。
逻辑回归由于其简单性和良好的解释性,是数据科学和机器学习领域常用的分类算法之一。无论是处理基础的二分类问题,还是用于更复杂的场景,逻辑回归都有着重要的应用价值。
相关文章:

Pytho逻辑回归算法:面向对象的实现与案例详解
这里写目录标题 Python逻辑回归算法:面向对象的实现与案例详解引言一、逻辑回归算法简介1.1 损失函数1.2 梯度下降 二、面向对象的逻辑回归实现2.1 类的设计2.2 Python代码实现2.3 代码详解 三、逻辑回归案例分析3.1 案例一:简单二分类问题问题描述数据代…...

AWS WAF实战指南:从入门到精通
1. 引言 Amazon Web Services (AWS) Web Application Firewall (WAF) 是一款强大的网络安全工具,用于保护Web应用程序免受常见的Web漏洞攻击。本文将带您从入门到精通,深入探讨AWS WAF的实际应用策略,并提供具体案例,帮助您更好地保护您的Web应用程序。 2. AWS WAF基础 …...
k8s的部署
一、K8S简介 Kubernetes中文官网:Kubernetes GitHub:github.com/kubernetes/kubernetes Kubernetes简称为K8s,是用于自动部署、扩缩和管理容器化应用程序的开源系统,起源于Google 集群管理工具Borg。 Kubernetes集群组件逻辑图…...

C# 两个进程/exe通讯方式 两个应用程序通讯方式
C# 两个exe通讯方式 两个应用程序通讯方式 1. 命名管道(Named Pipes) 1.1. 概述 命名管道是一种用于在同一台机器或网络中不同进程之间进行双向通信的机制。它支持同步和异步通信,适用于需要高效数据传输的场景。 1.2. 特点 双向通信&am…...
ubuntu下打开摄像头
ubuntu下打开摄像头 在Ubuntu下,你可以使用cheese,这是一个开源的摄像头应用程序。如果你还没有安装它,可以通过以下命令安装: sudo apt-get updatesudo apt-get install cheese 安装完成后,你可以通过命令行启动它: cheese 或者,你也可以使用ffmpeg来打开摄像头并进…...

ABAP 表转JSON格式
FUNCTION ZRFC_FI_SEND_PAYPLAN2BPM. *"---------------------------------------------------------------------- *"*"本地接口: *" IMPORTING *" VALUE(INPUT) TYPE ZSRFC_FI_SEND_PAYBPM_IN *" EXPORTING *" VAL…...
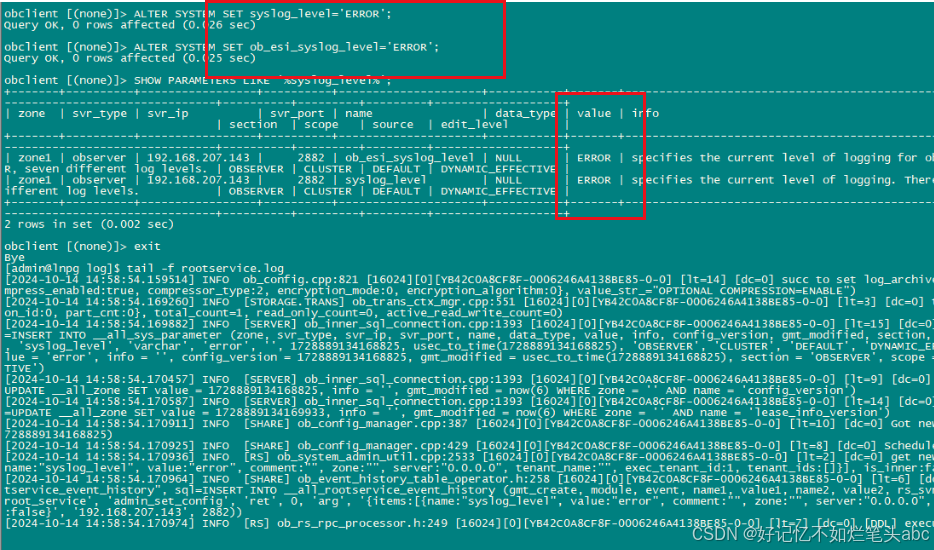
oceanbase的日志量太大,撑爆磁盘,修改下日志级别
oceanbase的日志量太大,撑爆磁盘,修改下日志级别: [adminlnpg ~]$ obclient -h127.0.0.1 -uroot -P2881 -plinux123 Welcome to the OceanBase. Commands end with ; or \g. Your OceanBase connection id is 3221561020 Server version: O…...

【C++11】lambda表达式
前言: 随着 C11 的发布,C 标准引入了许多新特性,使语言更加现代化,开发者编写的代码也变得更加简洁和易于维护。Lambda 表达式是其中一个重要的特性,它提供了一种方便的方式来定义匿名函数,这在函数式编程范…...

前端学习-css的背景(十六)
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 目录 前言 背景颜色 语法格式 背景图片 语法格式 背景平铺 语法格式 背景图片位置 语法格式 参数代表的意思 参数是方位名词 参数是精确单位 参数是混合单位 背…...

使用Postman搞定各种接口token实战
现在许多项目都使用jwt来实现用户登录和数据权限,校验过用户的用户名和密码后,会向用户响应一段经过加密的token,在这段token中可能储存了数据权限等,在后期的访问中,需要携带这段token,后台解析这段token才…...
ssh连接慢的问题或远程连接服务超时
问题原因: 在SSH登录过程中,服务器会通过反向DNS查找客户端的主机名,然后与登录的IP地址进行匹配,以验证登录的合法性。如果客户端的IP没有域名或DNS服务器响应缓慢,这可能导致SSH登录过慢。为了解决这个问题…...
基于卷积神经网络的蔬菜识别系统,resnet50,mobilenet模型【pytorch框架+python源码】
更多目标检测和图像分类识别项目可看我主页其他文章 功能演示: 基于卷积神经网络的蔬菜识别系统,resnet50,mobilenet【pytorch框架,python,tkinter】_哔哩哔哩_bilibili (一)简介 基于卷积神…...

数据结构与算法:栈与队列的高级应用
目录 3.1 栈的高级用法 3.2 队列的深度应用 3.3 栈与队列的综合应用 总结 数据结构与算法:栈与队列的高级应用 栈和队列是两种重要的线性数据结构,它们在计算机科学和工程的许多领域都有广泛的应用。从函数调用到表达式求值,再到任务调度…...

macos php开发环境之macport安装的php扩展安装,php常用扩展安装,port中可用的所有php扩展列表
macos中,我们使用了port 安装了php后,默认只带有php基本的核心扩展的, 如果需要使用其他的扩展,如 redis, https, xdebug等扩展就需要我们手动来安装对应的扩展。 macos php开发环境 macport安装的php的方法见macos 中…...

使用Pytorch+Numpy+Matplotlib实现手写字体分类和图像显示
文章目录 1.引用2.内置图片数据集加载3.处理为batch类型4.设置运行设备5.查看数据6.绘图查看数据图片(1)不显示图片标签(2)打印图片标签(3)图片显示标签 7.定义卷积函数8.卷积实例化、损失函数、优化器9.训练和测试损失、正确率(1)训练(2)测试(3)循环(4)损失和正确率曲线(5)输出…...

kimi帮我解决ubuntu下软链接文件夹权限不够的问题
我的操作如下 ubuntuubuntu-QiTianM420-N000:~$ ln -s /media/ubuntu/4701aea3-f883-40a9-b12f-61e832117414 code ubuntuubuntu-QiTianM420-N000:~$ ls -l 总用量 636 drwxrwxr-x 2 ubuntu ubuntu 4096 5月 7 17:16 bin drwxrwxrwx 2 ubuntu ubuntu 4096 5月 8 13…...

如何去除背景音乐保留人声?保留人声,消除杂音
在日常生活和工作中,我们经常遇到需要处理音频的情况,尤其是当我们想要去除背景音乐,仅保留人声时。这种需求在处理电影片段、制作音乐MV、或者提取演讲内容等场景中尤为常见。本文将为您详细介绍如何去除背景音乐并保留人声,帮助…...

2.4.ReactOS系统提升IRQL级别KfRaiseIrql 函数
2.4.ReactOS系统提升IRQL级别KfRaiseIrql 函数 2.4.ReactOS系统提升IRQL级别KfRaiseIrql 函数 文章目录 2.4.ReactOS系统提升IRQL级别KfRaiseIrql 函数KfRaiseIrql 函数 KfRaiseIrql 函数 /*********************************************************************** NAME …...

【新书】使用 OpenAI API 构建 AI 应用:利用 ChatGPT等构建 10 个 AI 项目(第二版),404页pdf
通过构建 ChatGPT 克隆、代码错误修复器、测验生成器、翻译应用、自动回复邮件生成器、PowerPoint 生成器等项目,提升您的应用开发技能。 关键特性 通过掌握 ChatGPT 概念(包括微调和集成),转变为 AI 开发专家 通过涵盖广泛 AI …...

修改PostgreSQL表中的字段排列顺序
二、通过修改系统表(pg_attribute)达到字段重新排序的目的有关系统表的概述及用途可以查看官网:http://www.pgsqldb.org/pgsqldoc-cvs/catalogs.html 表名字表用途pg_class表,索引,序列,视图(”关系”)pg_…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...

AI+无人机如何守护濒危物种?YOLOv8实现95%精准识别
【导读】 野生动物监测在理解和保护生态系统中发挥着至关重要的作用。然而,传统的野生动物观察方法往往耗时耗力、成本高昂且范围有限。无人机的出现为野生动物监测提供了有前景的替代方案,能够实现大范围覆盖并远程采集数据。尽管具备这些优势…...

PostgreSQL——环境搭建
一、Linux # 安装 PostgreSQL 15 仓库 sudo dnf install -y https://download.postgresql.org/pub/repos/yum/reporpms/EL-$(rpm -E %{rhel})-x86_64/pgdg-redhat-repo-latest.noarch.rpm# 安装之前先确认是否已经存在PostgreSQL rpm -qa | grep postgres# 如果存在࿰…...

MySQL:分区的基本使用
目录 一、什么是分区二、有什么作用三、分类四、创建分区五、删除分区 一、什么是分区 MySQL 分区(Partitioning)是一种将单张表的数据逻辑上拆分成多个物理部分的技术。这些物理部分(分区)可以独立存储、管理和优化,…...
