如何去除背景音乐保留人声？保留人声，消除杂音

在日常生活和工作中，我们经常遇到需要处理音频的情况，尤其是当我们想要去除背景音乐，仅保留人声时。这种需求在处理电影片段、制作音乐MV、或者提取演讲内容等场景中尤为常见。本文将为您详细介绍如何去除背景音乐并保留人声，帮助您轻松应对各种音频处理挑战。

一、使用专业音频编辑软件

专业的音频编辑软件，如Audacity、Adobe Audition等，是处理这类问题的首选工具。这些软件配备了频谱分析、噪音消除等高级功能，能够精确地识别和分离人声与背景音乐。

1.导入音频：首先，将您的音频文件导入到软件中。

2.频谱分析：利用频谱分析工具观察音频的波形和频率分布，这有助于您更准确地识别人声和背景音乐的差异。

3.噪音消除或声音分离：应用噪音消除功能或声音分离插件，通过调整参数来减少或消除背景音乐，同时尽量保持人声的清晰。

4.预览与导出：在处理过程中不断预览效果，直到满意为止。最后，导出处理后的音频文件。

二、借助智能音频处理工具

随着AI技术的不断进步，市面上已经出现了许多智能音频处理工具。这些工具能够自动识别音频中的人声和背景音乐，并提供一键式的分离功能。例如，易我人声分离就是一款免费的AI在线音频处理工具，操作简单便捷。

以下是这款工具的具体使用方法：

步骤1.访问并登录易我人声分离官网页面，选择“人声分离”功能。

步骤2.点击“选择文件”，把音频或者视频文件上传到网页窗口中(或者直接拖拽文件到窗口中)，等待AI处理。

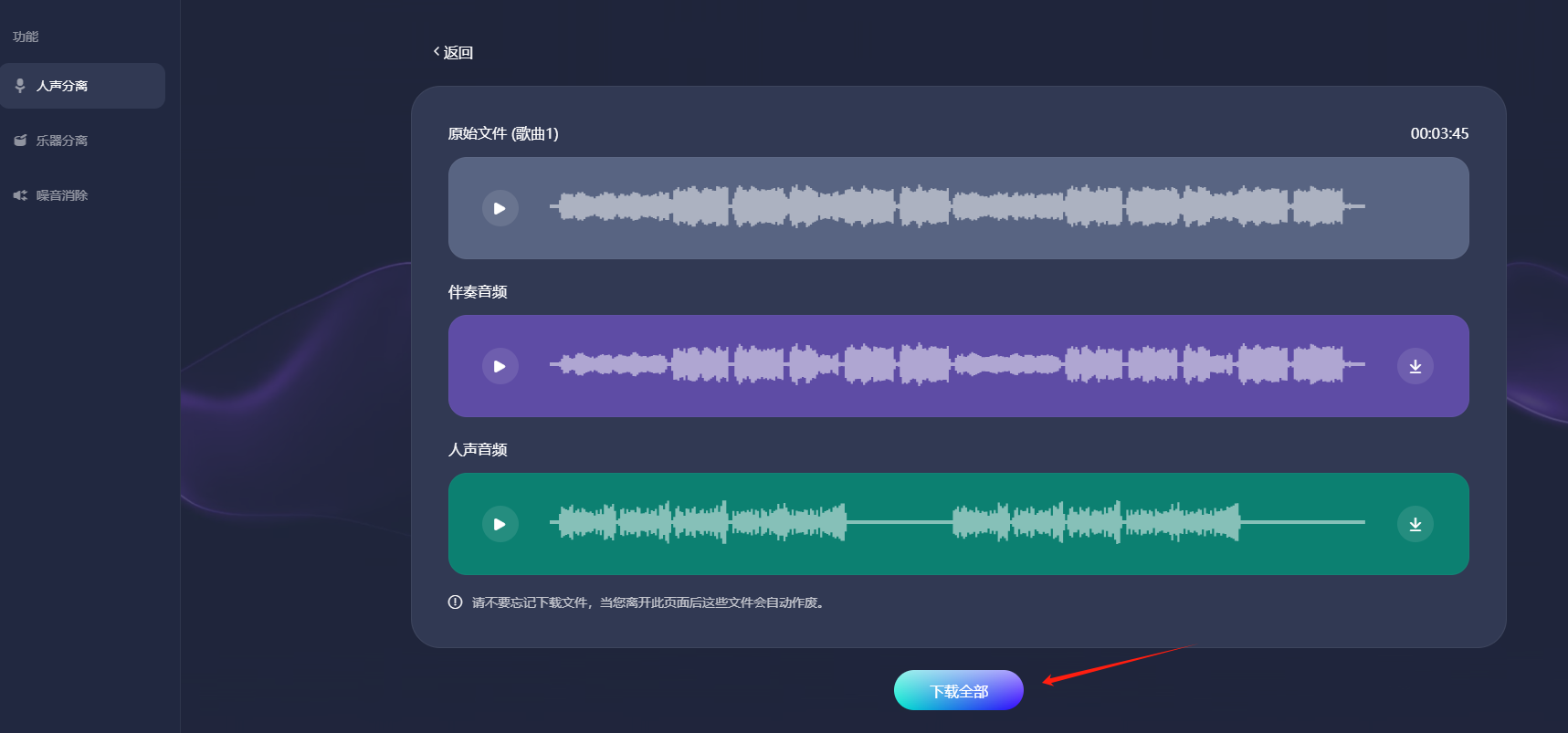
步骤3.AI处理完成后，会生成伴奏音频和人声音频，点击“下载全部”即可把音频下载到您的电脑上。

注意：请不要忘记下载文件，当您离开此页面后这些文件会自动作废。

三、寻求专业音频处理服务

如果您对音频处理的要求非常高，或者自己没有时间和精力去处理这些复杂的编辑工作，那么寻求专业的音频处理服务可能是一个更好的选择。许多专业的音频工作室或在线平台都提供音频分离、噪音消除等高级服务，他们拥有丰富的经验和专业的设备，能够确保您得到满意的处理结果。

四、注意事项

在处理音频时，有几点需要注意：

1.选择高质量的原始音频文件：高质量的音频文件更容易得到好的处理效果。

2.保持耐心并不断尝试：音频处理可能需要反复尝试和调整参数，以达到最佳效果。

3.控制背景音乐的音量：在录制音频时，尽量控制好背景音乐的音量，以减少后期处理的难度。

五、结语

去除背景音乐并保留人声是音频处理中的一项重要技能。无论是专业音频编辑软件、智能音频处理工具，还是专业音频处理服务，都能帮助您实现这一目标。

选择适合自己的方法和工具，您将能够轻松应对各种音频处理挑战，提升您的音频编辑能力。希望本文介绍的方法能对您有所帮助!