22年408数据结构
第一题:
解析:
观察一下这个程序:我们注意到最外层的循环是从i=1开始的,每次i=i*2,直到i<n为止,假设程序总共执行k次执行,则有2^(k+1)>=n。则k+1>=log(2)n这里是以2为底n的对数,
k>=log(2)n -1
我们再来看内层循环的特点:
i=1时 i=2时 i=4时 。。。 i=2^k
j=1 j=1 j=1 。。。 j=1
j=2 j=2 。。。 j=2
j=3 。。。 j=3
j=4 。。。 j=4
。。。 。。。
。。。 j=2^k
我们来试着算一下内层循环一共执行了多少次:
(这显然是一个等比数列,我们可以使用等比数列求和公式
)
,把k的值log(2)n -1带入进去。
,结果是一个线性的表达式,选项B最接近。
答案选B。
第二题:
解析:
A B明显错,我们做了这么多道推出栈顺序和入栈顺序的题了,看CD,如果入栈序列是abc
那么出栈序列也有可能是abc,只需要符号abc在入栈之后立刻出栈就好了,我们都知道栈有个特点是先进后出,输出的是栈顶元素,如果入栈序列是abc,依次将栈顶元素输出后的序列是cba。是逆序,显然D对
答案选D。
第三题:
解析:中序序列是左根右,题目要求p在q之前。
第一句:q是p的双亲,也就是说q是根结点,p是q的子结点,而且要求p在q之前,根据左根右可知,当p是q的左子树时满足条件。
第二句:q是p的右孩子,p是根结点,根据左根右,q一定在p的后面,满足条件。
第三句:根据左根右,左子树先被遍历,接着是根结点,然后才是q结点,因此在q前面的是根结点,不满足条件。
第四句:当p是q的左子树的右子树时满足条件。
答案选A。
第四题:
解析:
这就是一个简单的计算题,我们直接设这个三叉树的高度是h,题目要树的高度最少是多少,就是要让每一层的结点尽可能的最多,也就是满三叉树。那这样我们直接算高度为h的慢三叉树的结点个数是多少,
(这显然是一个等比数列求和问题),直接把选项往里一带:
高度为8的满三叉树结点个数有:3280,
高度为7的满三叉树结点个数有:1093,
高度为6的满三叉树结点个数有:364,
高度为5的满三叉树结点个数有:121,
本题说该三叉树结点个数244,在121和364之间。
也就是说该三叉树是高度为6的非满三叉树。高度至少是6.
答案选C。
第五题:
解析:这种题就是举例子。
以1,2,3为例,画一个哈夫曼树:
对于一个定长编码,它的字符都是处于同一层才能使编码长度一致。
观察两幅图可知,两颗二叉树结点的个数显然不一致,A错。
两颗二叉树的高度显然是一致的,B错。
显然a和b是出于同一层的,C错。
对于一个定长编码,它的字符显然是处于同一层的,D对。
答案选D。
第六题:
解析:|V|指的是顶点数,|E|指的是边。
A显然不正确,当顶点数是100个,而边只有一个显然不是连通图。
B举例:
,边有6条,而顶点只有5个,而且不是连通图。
C我们说要想让一个图是连通的,边的数量至少是顶点的个数减一,而选项中边的个数甚至比顶点的个数还多一个,显然想要连通是错错有余的,C正确
D选项,边的个数至少要比顶点的个数少一个才能连通,而此时|E|<|V|-1,连最低的边的个数都达不到,D错误。
答案选C。
第七题:
解析:
答案选B。
第八题:
解析:
在5阶B树中,根结点的关键字个数最少是1个,最多是5-1=4个。
在除叶子结点以外的非根结点中,关键字个数最少是[5/2]向上取整-1=2个,最多是5-1=4个
在B树中,删除一个节点,如果关键字中的个数不符合B树的定义的话就需要调整,符合个数也可以调整,具体的调整方法,可以把该点的前驱,或者后继添补上这个空缺。
选项A:选择260的后继结点280来填补空缺,但是这样的话,右子树中的关键字个数只剩下了300,而我们说非叶子结点关键字个数最少是2个(注意下面一层是终端结点,不是叶子结点不要误会了。),我们就将300的后继结点350从根结点上移下来,与300,400,500一起合并成一个结点:
选项B:把260删除后,直接将100,110,280,300合并成了一个结点,且符合B树的定义。
选项C:
显然是对的。
选项D:90和110之间只有一个100,不符合最少2个关键字的设定,所以D错。
答案选B。
第九题:
解析:
1.装填因子越大,代表散列表中装填的个数越多,冲突的可能性越大,查找次数就会越大,所以第一句对,
2.散列函数以这两个为例:
显然对3取余比对7取余的更容易发生冲突,第二句也对。
3. 线性探测法很容易造成同义词,非同义词的聚集堆积现象,严重影响查找效率,就拿线性探测法和平方探测法来比较说,显然线性探测法的查找效率差,自然影响平均查找长度。
下表是不同方式处理冲突时的平均查找长度。
答案选D。
第十题:
解析:
将两个有序表合并成一个新的有序表:
答案选A。
第十一题:
解析:该题考察直接插入排序和快速排序的比较。
1.对于一个大部分有序的序列,不适合采用快速排序,这是一个老生常谈的问题了,所以第一句是对的。2.对于一个元素数量很少的序列,好像使用直接插入排序还是快速排序好像都挺快的,先放着,不过直接插入排序要更简单直接一点。3.直接插入排序是原地进行的,空间复杂度是O(1),快速排序空间复杂度最好log(2)n,最坏O(n),第三句正确,直接插入排序是稳定的。第四句对,科普一下:稳定的排序算法有:冒泡排序,归并排序,插入排序,基数排序,计数排序(未出现过)。
包括1和3的只有D。
答案选D。
相关文章:

22年408数据结构
第一题: 解析: 观察一下这个程序:我们注意到最外层的循环是从i1开始的,每次ii*2,直到i<n为止,假设程序总共执行k次执行,则有2^(k1)>n。则k1>log(2)n这里是以2为底n的对数, k>log(2)…...
ubuntu 虚拟机将linux文件夹映射为windows网络位置
在使用虚拟机时可以选择将windows的文件夹设置为共享文件夹方便在虚拟机中访问windows中的文件,同理,也可以将linux的文件夹共享为一个网络文件夹,通过windows的添加一个网络位置功能,将linux的文件夹映射到windows本地,方便windows访问使用linux的文件夹 参照如下:https://blo…...

Pytho逻辑回归算法:面向对象的实现与案例详解
这里写目录标题 Python逻辑回归算法:面向对象的实现与案例详解引言一、逻辑回归算法简介1.1 损失函数1.2 梯度下降 二、面向对象的逻辑回归实现2.1 类的设计2.2 Python代码实现2.3 代码详解 三、逻辑回归案例分析3.1 案例一:简单二分类问题问题描述数据代…...

AWS WAF实战指南:从入门到精通
1. 引言 Amazon Web Services (AWS) Web Application Firewall (WAF) 是一款强大的网络安全工具,用于保护Web应用程序免受常见的Web漏洞攻击。本文将带您从入门到精通,深入探讨AWS WAF的实际应用策略,并提供具体案例,帮助您更好地保护您的Web应用程序。 2. AWS WAF基础 …...
k8s的部署
一、K8S简介 Kubernetes中文官网:Kubernetes GitHub:github.com/kubernetes/kubernetes Kubernetes简称为K8s,是用于自动部署、扩缩和管理容器化应用程序的开源系统,起源于Google 集群管理工具Borg。 Kubernetes集群组件逻辑图…...

C# 两个进程/exe通讯方式 两个应用程序通讯方式
C# 两个exe通讯方式 两个应用程序通讯方式 1. 命名管道(Named Pipes) 1.1. 概述 命名管道是一种用于在同一台机器或网络中不同进程之间进行双向通信的机制。它支持同步和异步通信,适用于需要高效数据传输的场景。 1.2. 特点 双向通信&am…...
ubuntu下打开摄像头
ubuntu下打开摄像头 在Ubuntu下,你可以使用cheese,这是一个开源的摄像头应用程序。如果你还没有安装它,可以通过以下命令安装: sudo apt-get updatesudo apt-get install cheese 安装完成后,你可以通过命令行启动它: cheese 或者,你也可以使用ffmpeg来打开摄像头并进…...

ABAP 表转JSON格式
FUNCTION ZRFC_FI_SEND_PAYPLAN2BPM. *"---------------------------------------------------------------------- *"*"本地接口: *" IMPORTING *" VALUE(INPUT) TYPE ZSRFC_FI_SEND_PAYBPM_IN *" EXPORTING *" VAL…...
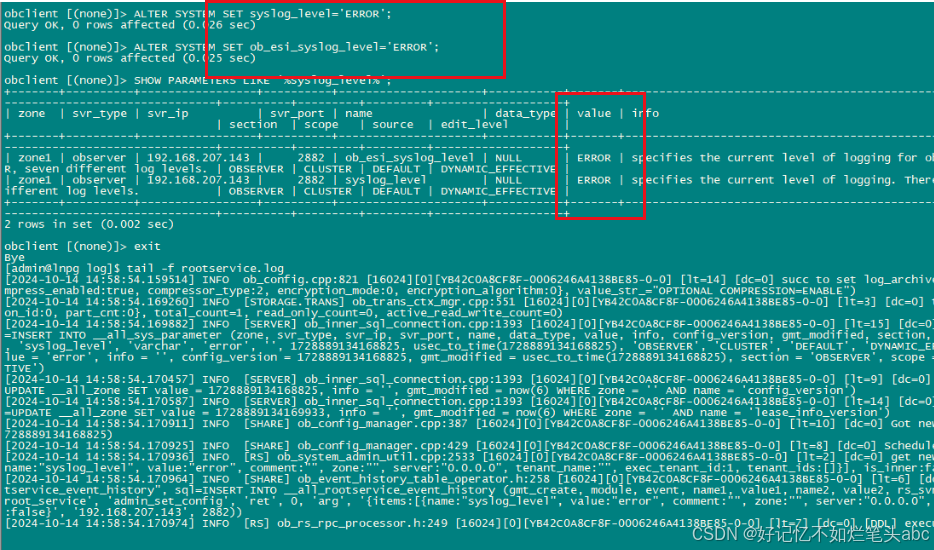
oceanbase的日志量太大,撑爆磁盘,修改下日志级别
oceanbase的日志量太大,撑爆磁盘,修改下日志级别: [adminlnpg ~]$ obclient -h127.0.0.1 -uroot -P2881 -plinux123 Welcome to the OceanBase. Commands end with ; or \g. Your OceanBase connection id is 3221561020 Server version: O…...

【C++11】lambda表达式
前言: 随着 C11 的发布,C 标准引入了许多新特性,使语言更加现代化,开发者编写的代码也变得更加简洁和易于维护。Lambda 表达式是其中一个重要的特性,它提供了一种方便的方式来定义匿名函数,这在函数式编程范…...

前端学习-css的背景(十六)
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 目录 前言 背景颜色 语法格式 背景图片 语法格式 背景平铺 语法格式 背景图片位置 语法格式 参数代表的意思 参数是方位名词 参数是精确单位 参数是混合单位 背…...

使用Postman搞定各种接口token实战
现在许多项目都使用jwt来实现用户登录和数据权限,校验过用户的用户名和密码后,会向用户响应一段经过加密的token,在这段token中可能储存了数据权限等,在后期的访问中,需要携带这段token,后台解析这段token才…...
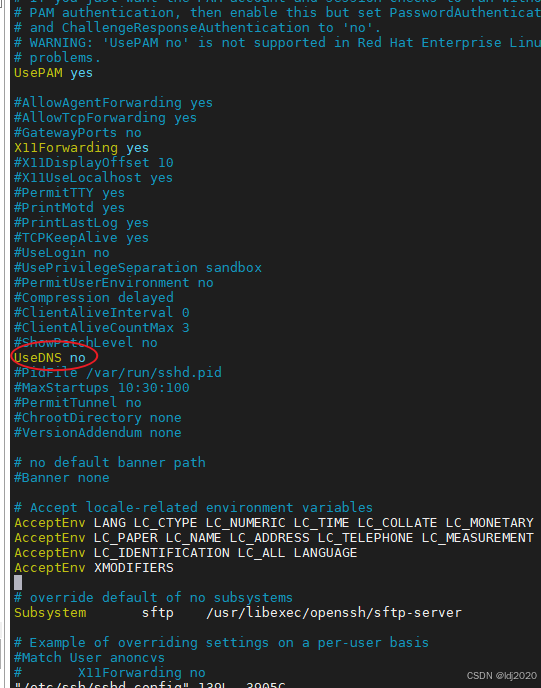
ssh连接慢的问题或远程连接服务超时
问题原因: 在SSH登录过程中,服务器会通过反向DNS查找客户端的主机名,然后与登录的IP地址进行匹配,以验证登录的合法性。如果客户端的IP没有域名或DNS服务器响应缓慢,这可能导致SSH登录过慢。为了解决这个问题…...
基于卷积神经网络的蔬菜识别系统,resnet50,mobilenet模型【pytorch框架+python源码】
更多目标检测和图像分类识别项目可看我主页其他文章 功能演示: 基于卷积神经网络的蔬菜识别系统,resnet50,mobilenet【pytorch框架,python,tkinter】_哔哩哔哩_bilibili (一)简介 基于卷积神…...

数据结构与算法:栈与队列的高级应用
目录 3.1 栈的高级用法 3.2 队列的深度应用 3.3 栈与队列的综合应用 总结 数据结构与算法:栈与队列的高级应用 栈和队列是两种重要的线性数据结构,它们在计算机科学和工程的许多领域都有广泛的应用。从函数调用到表达式求值,再到任务调度…...

macos php开发环境之macport安装的php扩展安装,php常用扩展安装,port中可用的所有php扩展列表
macos中,我们使用了port 安装了php后,默认只带有php基本的核心扩展的, 如果需要使用其他的扩展,如 redis, https, xdebug等扩展就需要我们手动来安装对应的扩展。 macos php开发环境 macport安装的php的方法见macos 中…...

使用Pytorch+Numpy+Matplotlib实现手写字体分类和图像显示
文章目录 1.引用2.内置图片数据集加载3.处理为batch类型4.设置运行设备5.查看数据6.绘图查看数据图片(1)不显示图片标签(2)打印图片标签(3)图片显示标签 7.定义卷积函数8.卷积实例化、损失函数、优化器9.训练和测试损失、正确率(1)训练(2)测试(3)循环(4)损失和正确率曲线(5)输出…...

kimi帮我解决ubuntu下软链接文件夹权限不够的问题
我的操作如下 ubuntuubuntu-QiTianM420-N000:~$ ln -s /media/ubuntu/4701aea3-f883-40a9-b12f-61e832117414 code ubuntuubuntu-QiTianM420-N000:~$ ls -l 总用量 636 drwxrwxr-x 2 ubuntu ubuntu 4096 5月 7 17:16 bin drwxrwxrwx 2 ubuntu ubuntu 4096 5月 8 13…...

如何去除背景音乐保留人声?保留人声,消除杂音
在日常生活和工作中,我们经常遇到需要处理音频的情况,尤其是当我们想要去除背景音乐,仅保留人声时。这种需求在处理电影片段、制作音乐MV、或者提取演讲内容等场景中尤为常见。本文将为您详细介绍如何去除背景音乐并保留人声,帮助…...

2.4.ReactOS系统提升IRQL级别KfRaiseIrql 函数
2.4.ReactOS系统提升IRQL级别KfRaiseIrql 函数 2.4.ReactOS系统提升IRQL级别KfRaiseIrql 函数 文章目录 2.4.ReactOS系统提升IRQL级别KfRaiseIrql 函数KfRaiseIrql 函数 KfRaiseIrql 函数 /*********************************************************************** NAME …...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...

10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI,使用客户端或是内部自己搭建集成大模型的终端,加速与大型语言模型(LLM)的结合,同时使用检索增强生成(Retrieval Augmented Generation &#…...

python报错No module named ‘tensorflow.keras‘
是由于不同版本的tensorflow下的keras所在的路径不同,结合所安装的tensorflow的目录结构修改from语句即可。 原语句: from tensorflow.keras.layers import Conv1D, MaxPooling1D, LSTM, Dense 修改后: from tensorflow.python.keras.lay…...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...

return this;返回的是谁
一个审批系统的示例来演示责任链模式的实现。假设公司需要处理不同金额的采购申请,不同级别的经理有不同的审批权限: // 抽象处理者:审批者 abstract class Approver {protected Approver successor; // 下一个处理者// 设置下一个处理者pub…...

力扣热题100 k个一组反转链表题解
题目: 代码: func reverseKGroup(head *ListNode, k int) *ListNode {cur : headfor i : 0; i < k; i {if cur nil {return head}cur cur.Next}newHead : reverse(head, cur)head.Next reverseKGroup(cur, k)return newHead }func reverse(start, end *ListNode) *ListN…...

【Nginx】使用 Nginx+Lua 实现基于 IP 的访问频率限制
使用 NginxLua 实现基于 IP 的访问频率限制 在高并发场景下,限制某个 IP 的访问频率是非常重要的,可以有效防止恶意攻击或错误配置导致的服务宕机。以下是一个详细的实现方案,使用 Nginx 和 Lua 脚本结合 Redis 来实现基于 IP 的访问频率限制…...























