如何缩短微商城系统推广周期
前言
微商城系统的推广周期是企业关注的重点之一。为了缩短推广周期,企业需要采取一系列有效的策略和措施。以下是对如何缩短微商城系统推广周期的详细介绍:
一、明确目标用户群体
在推广之前,企业需要明确自己的目标用户群体是谁,了解他们的需求、兴趣和行为习惯,以便制定更有针对性的推广策略。通过深入了解目标用户,企业可以更精准地定位市场,提高推广效果。
二、制定详细的推广计划
根据目标用户群体的特点,企业需要制定详细的推广计划,包括推广渠道、时间安排、预算分配等。一个完善的推广计划可以帮助企业更好地组织和管理推广活动,确保推广工作的有序进行。
三、利用多种推广渠道
企业应充分利用各种推广渠道,如社交媒体、搜索引擎优化、广告投放等,扩大品牌曝光度,吸引更多潜在用户。同时,企业还可以考虑与其他相关企业或平台进行合作,共同开展推广活动,实现资源共享和互利共赢。
四、提供优质的产品和服务
优质的产品和服务是吸引用户的关键。企业需要注重产品质量和服务质量的提升,以满足用户的需求和期望。通过提供优质的服务和产品,企业可以赢得用户的信任和口碑传播,进一步推动微商城的发展。
五、加强用户互动和沟通
与用户进行互动和沟通是建立良好关系的重要手段。企业可以通过社交媒体、在线客服等方式与用户保持联系,及时回应用户的疑问和反馈,解决用户的问题。同时,企业还可以通过举办线上线下活动、发布优惠信息等方式增加用户的参与度和忠诚度。
六、持续优化和改进
推广工作是一个持续的过程,企业需要不断优化和改进推广策略和方法。通过数据分析和用户反馈收集,企业可以了解推广效果和用户需求的变化情况,及时调整推广策略和方法以适应市场变化。
七、利用数据分析工具
利用数据分析工具可以帮助企业更好地了解用户行为和需求变化情况。通过对用户数据的分析和挖掘,企业可以发现潜在的机会和问题点并及时进行调整和优化。同时,数据分析工具还可以帮助企业评估推广效果和ROI(投资回报率)为未来的推广决策提供有力支持。
八、建立品牌形象和口碑
品牌形象和口碑是吸引用户的重要因素之一。企业需要注重品牌形象的塑造和维护以及口碑的传播和积累。通过提供优质的产品和服务、加强用户互动和沟通等方式建立良好的品牌形象和口碑可以进一步提高用户的信任度和忠诚度促进微商城的发展。
九、创新推广方式
随着互联网技术的不断发展新的推广方式也不断涌现。企业可以尝试采用一些创新的推广方式如短视频营销、直播带货等来吸引年轻用户的关注并提高品牌曝光度和知名度。同时企业还可以结合线下活动和线上推广相结合的方式打造全方位的营销体验提升用户参与度和转化率。
十、合理控制预算
在推广过程中企业需要合理控制预算避免过度投入导致资源浪费。通过制定详细的预算计划和监控推广成本企业可以确保在有限的预算内实现最大的推广效果。同时企业还需要根据实际情况灵活调整预算分配以确保推广活动的顺利进行。
总结
综上所述,缩短微商城系统推广周期需要企业在多个方面下功夫。通过明确目标用户群体、制定详细的推广计划、利用多种推广渠道、提供优质的产品和服务、加强用户互动和沟通、持续优化和改进、利用数据分析工具、建立品牌形象和口碑、创新推广方式以及合理控制预算等措施的实施,企业可以有效缩短推广周期,提高推广效果,进一步推动微商城的发展。
相关文章:

如何缩短微商城系统推广周期
前言 微商城系统的推广周期是企业关注的重点之一。为了缩短推广周期,企业需要采取一系列有效的策略和措施。以下是对如何缩短微商城系统推广周期的详细介绍: 一、明确目标用户群体 在推广之前,企业需要明确自己的目标用户群体是谁…...

电脑如何清理重复文件?方法很简单!
清理重复文件能够有效释放存储空间,提高系统运行效率。长期堆积的重复文件会导致硬盘空间不足,从而影响系统性能。此外,清理文件还能帮助用户更好地管理和组织文件,避免因文件混乱而浪费时间。 常见的重复文件类型 重复文件可以是…...

【Linux】ioctl分析
简介 一个字符设备驱动通常会实现常规的open、release、read和write接口,但是如果需要扩展新的功能,通常以ioctl接口的方式实现。 #mermaid-svg-uY8EyPklf5e4ZMQo {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill…...

物联网通信会给人们的生活带来什么样的变化
物联网(IoT)通信的崛起正以前所未有的速度改变着人们的生活方式。从智能家居、智能交通到远程医疗、工业自动化,物联网技术的应用已经渗透到我们日常生活的方方面面。以下是对物联网通信如何具体影响并改变人们生活的详细探讨。 一、智能家居…...

Android 中获取当前 CPU 频率和占用率
最近在优化 App 的性能,需要获取当前 CPU视频频率和占用率,通过查询资料,大致思路如下: 目前没有标准的 API 来获取 CPU 的使用频率,只能通过读取指定 CPU 文件获取当前 CPU 频率,在某些机器或者特定版本中…...

pymobiledevice3使用介绍(安装、常用命令、访问iOS沙盒目录)
项目地址:https://github.com/doronz88/pymobiledevice3 首先先介绍一下pymobiledevice3, pymobiledevice3是用Python3 实现的,用于处理 iDevices(iPhone 等)。它可以跨平台使用,支持:windows…...

python 爬虫模拟登录
在使用 Python 编写爬虫时,模拟登录是一个非常常见的需求,尤其是当你需要爬取需要身份验证的数据时。模拟登录通常需要以下步骤: 分析登录页面:确定提交登录请求的 URL 和相关参数。发送登录请求:模拟用户发送登录表单…...

AOP基础、快速入门、进阶
一、概述 AOP:Aspect Oriented Programming(面向切面编程、面向方面编程),其实就是面向特定方法编程 那什么又是面向方法编程呢,为什么又需要面向方法编程呢?来我们举个例子做一个说明: 比如…...

哪款宠物空净运行吸毛好、噪音小?希喂、霍尼韦尔、安德迈测评!
作为宠物领域目前最火热的产品,宠物空气净化器的讨论度一直很高。身为铲屎官的我在产品刚出的时候就购入了一台,结果让我非常失望! 抛开产品效果不提,它运行起来的声音实在太大了!我家猫根本不愿意靠近,每…...

新兴的安全职业挑战
我们经常与安全专业人士交谈,他们希望在努力提升职业发展的同时提高自己的价值并克服组织内部的挑战。在这些谈话中,花费大量时间讨论公司未来将面临的安全问题并不罕见。 安全领导者希望为问题制定计划并获得领导层对其计划的支持。这通常意味着实施修…...
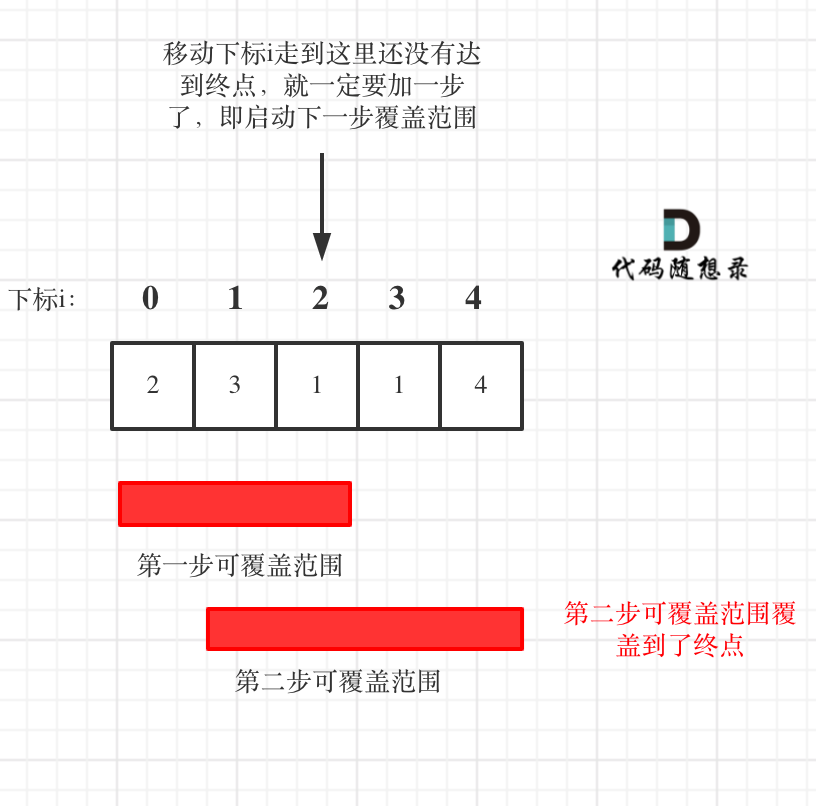
代码随想录算法训练营Day32 | 122.买卖股票的最佳时机Ⅱ、55.跳跃游戏、45.跳跃游戏Ⅱ、1005.K次取反后最大化的数组和
目录 122.买卖股票的最佳时机Ⅱ 55.跳跃游戏 45.跳跃游戏Ⅱ 1005.K次取反后最大化的数组和 122.买卖股票的最佳时机Ⅱ 题目 122. 买卖股票的最佳时机 II - 力扣(LeetCode) 给你一个整数数组 prices ,其中 prices[i] 表示某支股票第 i…...

3D Slicer 教程一
先了解一下什么是3D Slicer,这个是做什么,然后一步步了解功能,一起看看源码 一.初识 这块软件用来处理医学影像,是一款开源的软件. 里面涉及到一些 2d 常见的操作,图像处理,调窗,测量; 涉及到3d的一些常见重建,mpr,vr,cpr等, 还包括一些分割,变换等(越高级精确的一些通过插件…...

github pages + hugo 搭建静态博客网站
体验地址 1. 起因, 目的: 其实6年前,我就写过这个。 项目代码 博客地址 最近想改写一下。 github 推荐的主题是 Jekyll, 我当时用的就是这个,感觉很麻烦。尤其是文章命名。 新的主题 hugo 用起来还行。 2.过程: 过程记录&am…...

Python爬虫如何爬取并解析JSON数据
前言 Python爬虫是一种用于从互联网上获取数据的程序,而JSON(JavaScript Object Notation)是一种常用的数据交换格式。本文将介绍如何使用Python爬虫来爬取并解析JSON数据,同时还会讲解如何使用代理IP来提高爬取效率。 1. 什么是…...

【C++】精妙的哈希算法
🚀个人主页:小羊 🚀所属专栏:C 很荣幸您能阅读我的文章,诚请评论指点,欢迎欢迎 ~ 目录 一、哈希结构1、哈希概念2、哈希函数3、哈希冲突3.1 闭散列3.2 开散列 4、完整代码 一、哈希结构 1、哈希概念 A…...

智慧链动青春:国家区块链中心接待北京市十一学校青少年访学探索
以生动科学的方法点燃青少年科学探索欲望是构建未来科技人才梯队的基石。近期国家区块链技术创新中心接待北京市十一学校新生访学,以科普讲座、实操互动的方式让学生在深度思考中感受科学魅力、接触前沿科技,激发学生对区块链、隐私计算和芯片设计制造的…...

利用C++封装鼠标轨迹算法为DLL:游戏行为检测的利器
在现代软件开发中,鼠标轨迹模拟技术因其在自动化测试、游戏脚本编写等领域的广泛应用而备受青睐。本文将介绍如何使用C语言将鼠标轨迹算法封装为DLL(动态链接库),以便在多种编程环境中实现高效调用,同时探讨其在游戏行…...

Qt- QSS风格选择器常用属性选择器样式表盒子
1. 风格设置 Qt 提供了 3 种整体风格,使用 QStyleFactory::keys() 来获取 (windowsvista 、Windows 、Fusion) 可以在 main.cpp 中调用 setStyle 方法对应用程序进行全局风格的设置 int main(int argc, char *argv[]) {QApplication a(arg…...

粤智助自助一体机大厂浮出水面 OBOO鸥柏已成服务终端中坚力量
自助服务查询一体机作为操作自主化便民的重要窗口,OBOO鸥柏自助服务终端机以其显著的技术优化,通过触摸屏或其他交互界面,使用户能够自助服务完成各种操作,如支付、查询信息终端、办理业务,自助查档答应一体化等。为交…...

SpringBoot-application.properties配置
默认配置最终都是映射/关联到某个类 #SPRING CONFIG(ConfigFileApplicationListener) spring.config.name #配置文件名(默认 为 application ) spring.config.location #配置文件的位置 …...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...

MacOS下Homebrew国内镜像加速指南(2025最新国内镜像加速)
macos brew国内镜像加速方法 brew install 加速formula.jws.json下载慢加速 🍺 最新版brew安装慢到怀疑人生?别怕,教你轻松起飞! 最近Homebrew更新至最新版,每次执行 brew 命令时都会自动从官方地址 https://formulae.…...

前端中slice和splic的区别
1. slice slice 用于从数组中提取一部分元素,返回一个新的数组。 特点: 不修改原数组:slice 不会改变原数组,而是返回一个新的数组。提取数组的部分:slice 会根据指定的开始索引和结束索引提取数组的一部分。不包含…...

MySQL 主从同步异常处理
阅读原文:https://www.xiaozaoshu.top/articles/mysql-m-s-update-pk MySQL 做双主,遇到的这个错误: Could not execute Update_rows event on table ... Error_code: 1032是 MySQL 主从复制时的经典错误之一,通常表示ÿ…...
