集合论(ZFC)之良创关系(Well-Founded Relation)
定义在集合S中的一个二元关系(Binary Relation)记,<,有(S,<)。如果对于集合S的任意非空子集,都存在关系(<)下的最小元素,那么该关系(<)成为良创关系(Well_Founded Relation),集合S与关系(<),即(S,<),称为良创集。亦:
(s ⊂ S ∧ s ≠ ∅ → (a ∈ s → ¬(∃x∈s.(x < a)))) → Well_Founded(S)
可证,良序集(Well-Ordered Set)满足良创集的条件。即良序集为良创集。
另外,给定义一个良创集(S,<),可定义关系(<)的高度(height),同时,赋予集合S中的每个元素 x 一个序数,称该序数为对应元素 x 的关系(<)层级 ( Rank of x in < )。
那么,把这赋级规则看作是一函数 rank: S → Ordinal,其定义为
rank(x) = sup { rank(y) + 1: y < x } ( x ∈ S )
该函数 rank 是唯一存在的。其证明可通过对层级进行归纳,定义各层级集合,如
S₀ = ∅ ;
Sₙ₊₁ = {s ∈ S: ∀t(t < s → t ∈ Sₙ)};
Sₐ = ⋃ ᵢ<ₐ Sᵢ ( a 是极限序数(limit ordinal))
那么,有 S₀ ⊂ S₁ ⊂ ... ⊂ S。
令,r 为该集合的最高层级,有 Sᵣ = S。
如果 Sᵣ ≠ S,那么,(S - Sᵣ)⊂ S,而S为良创集,由此存在一个元素 a 是(S - Sᵣ)中,关系(<)下的最小元素,那么根据上述描述,a 存在于 Sᵣ₊₁ 中,与定义不符,因此,Sᵣ = S。
其中 r 为 良创集(S,<)的高度。
相关文章:
之良创关系(Well-Founded Relation))
集合论(ZFC)之良创关系(Well-Founded Relation)
定义在集合S中的一个二元关系(Binary Relation)记,<,有(S,<)。如果对于集合S的任意非空子集,都存在关系(<)下的最小元素,那么该关系&…...

centos 安装达梦数据库
一、环境准备 1.1、确认操作系统的版本和数据库的版本是否一致 ## 查看系统版本:cat /etc/redhat-release CentOS Linux release 7.5.1804 (Core)1.2、关闭防火墙和Selinux # 查看selinux是不是disabled / enforce cat /etc/selinux/config## 查看防火墙状态 fir…...

《Windows PE》6.4.1 无 DLL远程注入
本节我们将演示如何实现远程注入的两种不同方案。方案一选择远程注入代码和数据,方案二选择远程注入DLL。 本节必须掌握的知识点: 无DLL远程注入 远程注入DLL 6.4.1 无DLL远程注入 实验四十五:无DLL远程注入(C语言实现…...

浙大数据结构:10-排序6 Sort with Swap(0, i)
这道题用了数环的思想,MOOC最后视频中也有相关介绍,思想还是很巧妙的 机翻 1、思想 2、 主函数 先把数据存进来,然后从头开始遍历,如果该位置数不对则anwser,然后遍历整个环,一直加anwser,如…...

基于vue框架的的爱心捐赠物资信息系统85gsu(程序+源码+数据库+调试部署+开发环境)系统界面在最后面。
系统程序文件列表 项目功能:用户,爱心项目,捐赠类型,捐赠,积分兑换,兑换,捐赠名录,捐赠去向 开题报告内容 基于Vue框架的爱心捐赠物资信息系统开题报告 一、研究背景与意义 随着社会的发展和人们生活水平的提高,爱心捐赠活动逐渐成为连接捐赠者与受赠…...

AI对抗AI:如何应对自动化攻击新时代?
在当今这个生成式AI迅猛发展的时代,自动化攻击的威胁日益加剧。 在人工智能浪潮下,如何利用AI对抗AI,从而实现全方位的网络安全防护? 一、AI浪潮下,自动化攻击加剧 AI技术的发展既带来了前所未有的挑战,也…...

【微服务】微服务注册:构建灵活的服务管理机制
目录 引言一、什么是微服务注册?1.1 服务注册中心的作用1.2 服务注册中心的工作原理1.3 示意图 二、常见的微服务注册中心2.1 各注册中心详细对比 三、微服务注册的实现方式3.1 Spring Cloud Netflix Eureka3.2 Consul3.3 Zookeeper3.4 etcd 四、微服务注册的注意事…...

AsyncTask的工作原理和缺陷
AsyncTask的工作原理及其缺陷 AsyncTask是Android平台提供的一个轻量级的异步任务类,它允许开发者在后台线程中执行耗时操作,并在操作完成后将结果回调到主线程以更新UI。AsyncTask内部封装了线程池和Handler机制,简化了多线程编程的复杂性。…...

【React】事件绑定的方式
1. 内联函数绑定 这是最简单直接的方式,即在 JSX 语法中直接传递一个内联函数。这种方式每次渲染时都会创建新的函数实例,可能会导致不必要的性能开销。 class MyComponent extends React.Component {render() {return (<button onClick{() > th…...

Android ImageView scaleType使用
目录 一、src设置图片资源 二、scaleType设置图片缩放类型 三、scaleType具体表现 matrix: fitXY: fitStart: fitCenter: fitEnd: Center: centerCrop: centerInside: 控制ImageView和图片的大小保持一致…...

【PhpSpreadsheet】ThinkPHP5+PhpSpreadsheet实现批量导出数据
目录 前言 一、安装 二、API使用 三、完整实例 四、效果图 前言 为什么使用PhpSpreadsheet? 由于PHPExcel不再维护,所以建议使用PhpSpreadsheet来导出exlcel,但是PhpSpreadsheet由于是个新的类库,所以只支持PHP7.1及以上的版…...

Python剪辑视频
import os from moviepy.editor import VideoFileClipvideo_dir r"E:\学习\视频剪辑" s_video_file "1.mp4" d_video_file "剪辑片段1.mp4" s_video_path os.path.join(video_dir, s_video_file) # 原视频文件路径 d_video_path os.path…...
LabVIEW提高开发效率技巧----高效文件I/O
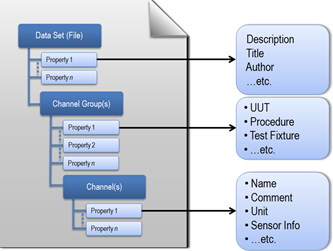
在LabVIEW开发中,文件I/O操作常常是性能瓶颈之一,特别是处理大数据时,如何高效地存储和读取数据显得尤为重要。本文将详细介绍如何利用TDMS Streaming来实现高效的文件I/O,并结合具体例子说明在实际开发中的应用技巧。 1. 什么是T…...

影刀RPA接口_查询应用主流程参数结构
影刀接口_查询应用主流程参数结构 链接 import requests from time import sleepaccessKeyId"XXX" accessKeySecret"XXX"#1.获取token def get_access_token():url"https://api.yingdao.com/oapi/token/v2/token/create"headers{"Content…...

2d实时数字人聊天语音对话使用案例,对接大模型
参看: https://github.com/wan-h/awesome-digital-human-live2d 电脑环境: ubuntu 1060ti 下载: git clone https://github.com/wan-h/awesome-digital-human-live2d.gitdocker部署; cd awesome-digital-human-live2d docker-compose -f docker-compose-quickStart.ya…...

LeetCode | 69.x的平方根
这道题很适合用二分来解决,算是二门入门的一个练手题吧思想就是首先设置两个指针,一个是0,一个是x,相当于在数轴上划定一个区域 [ 0 , x ]然后计算数轴中间值和我们想要找的值的大小关系,因为数轴是有序的,…...
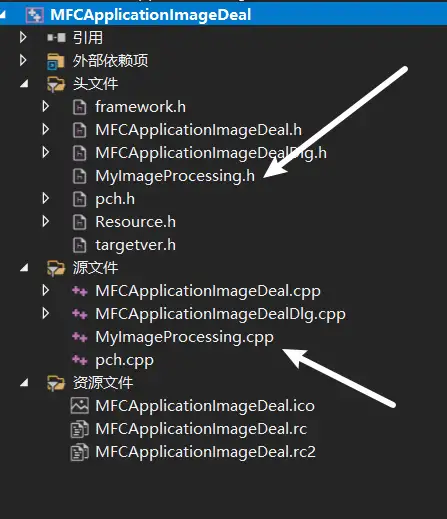
使用Windows创建一个MFC应用【带界面】
MFC使用教程【对初学者保姆型友好!】 目录 前提条件 1:创建MFC应用程序 2. 项目结构解读 引用 外部依赖项 头文件 源文件 资源文件 文件功能详解 项目的主要流程 步骤2:配置OpenCV 安装OpenCV 包含目录与库文件 步骤3࿱…...

springboot整合lombok
只需要引入lombok依赖 <dependency> <groupId>org.projectlombok</groupId> <artifactId>lombok</artifactId> <version>1.16.18</version></dependency> 然后application.yml配置文件中加上 logging: level: …...
使用Arcgis批量自动出图
操作方法如下: 1 2 3 4 5 6 7 设置好选项,开始打印。 8 生成pdf。 第一步:shp放到数据库中,标注转注记,然后编辑注记,符号样式设置好。准备出图:(转注记时候尽量压盖监测等选最…...

Web Worker加载外部文件实践
概述 在Web Worker 多线程编程一文中介绍了Web Worker的编程思想,碰巧最近工作中某个工程需要加载外部文件,最大的文件大小达到30MB,Web Worker无疑是不错的选择。 编程实现 不用 Web Worker 加载外部文件使用原生的fetch方法读取文件,其核心代码如下: function loadland…...
。】2022-5-15)
【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15
缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下: struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

【生成模型】视频生成论文调研
工作清单 上游应用方向:控制、速度、时长、高动态、多主体驱动 类型工作基础模型WAN / WAN-VACE / HunyuanVideo控制条件轨迹控制ATI~镜头控制ReCamMaster~多主体驱动Phantom~音频驱动Let Them Talk: Audio-Driven Multi-Person Conversational Video Generation速…...
的使用)
Go 并发编程基础:通道(Channel)的使用
在 Go 中,Channel 是 Goroutine 之间通信的核心机制。它提供了一个线程安全的通信方式,用于在多个 Goroutine 之间传递数据,从而实现高效的并发编程。 本章将介绍 Channel 的基本概念、用法、缓冲、关闭机制以及 select 的使用。 一、Channel…...

GitFlow 工作模式(详解)
今天再学项目的过程中遇到使用gitflow模式管理代码,因此进行学习并且发布关于gitflow的一些思考 Git与GitFlow模式 我们在写代码的时候通常会进行网上保存,无论是github还是gittee,都是一种基于git去保存代码的形式,这样保存代码…...

Git 3天2K星标:Datawhale 的 Happy-LLM 项目介绍(附教程)
引言 在人工智能飞速发展的今天,大语言模型(Large Language Models, LLMs)已成为技术领域的焦点。从智能写作到代码生成,LLM 的应用场景不断扩展,深刻改变了我们的工作和生活方式。然而,理解这些模型的内部…...

日常一水C
多态 言简意赅:就是一个对象面对同一事件时做出的不同反应 而之前的继承中说过,当子类和父类的函数名相同时,会隐藏父类的同名函数转而调用子类的同名函数,如果要调用父类的同名函数,那么就需要对父类进行引用&#…...
