数学建模算法与应用 第16章 优化与模拟方法
目录
16.1 线性规划
Matlab代码示例:线性规划求解
16.2 整数规划
Matlab代码示例:整数规划求解
16.3 非线性规划
Matlab代码示例:非线性规划求解
16.4 蒙特卡洛模拟
Matlab代码示例:蒙特卡洛模拟计算圆周率
习题 16
总结
优化与模拟方法是解决复杂系统中的资源配置、路径选择、风险分析等问题的重要工具。优化方法用于寻找系统中的最优解,而模拟方法则用于模拟和分析系统的行为,以帮助决策者理解系统的复杂性并进行有效的规划和管理。本章将介绍几种常用的优化与模拟方法,包括线性规划、整数规划、蒙特卡洛模拟以及它们在Matlab中的应用。
16.1 线性规划
线性规划是一种求解线性目标函数在一组线性约束条件下的最优化问题的方法,广泛应用于生产、物流、资源分配等领域。
-
标准形式:线性规划的目标是最大化或最小化线性目标函数,约束条件通常表示为线性等式或不等式。
-
可行解与最优解:在满足所有约束条件的解集中,找到使目标函数值达到最优的解。
Matlab代码示例:线性规划求解
% 定义目标函数系数(最小化问题)
f = [-2, -3, -4];% 定义不等式约束
A = [3, 2, 1; 2, 5, 3];
B = [10; 15];% 定义变量的下界
lb = zeros(3, 1);% 使用linprog函数求解线性规划
[x, fval] = linprog(f, A, B, [], [], lb);% 输出最优解和最优值
disp('最优解:');
disp(x);
disp('最优目标函数值:');
disp(-fval);在上述代码中,我们使用linprog函数求解了一个简单的线性规划问题,得到了最优解和最优目标函数值。
16.2 整数规划
整数规划是线性规划的一种特殊形式,要求决策变量必须是整数,适用于许多离散的优化问题,如设备选址、车辆路径规划等。
-
整数约束:在整数规划中,所有或部分决策变量必须是整数。
-
混合整数规划:包含整数变量和连续变量的优化问题称为混合整数规划。
Matlab代码示例:整数规划求解
% 定义目标函数系数(最大化问题)
f = [5, 7];% 定义不等式约束
A = [1, 0; 0, 2; 3, 2];
B = [16; 19; 36];% 定义变量的下界和整数约束
lb = zeros(2, 1);
intcon = 1:2;% 使用intlinprog函数求解整数规划
[x, fval] = intlinprog(-f, intcon, A, B, [], [], lb);% 输出最优解和最优目标函数值
disp('最优解:');
disp(x);
disp('最优目标函数值:');
disp(-fval);在该代码中,我们使用intlinprog函数求解了一个整数规划问题,得到了最优解和对应的目标函数值。
16.3 非线性规划
非线性规划用于求解目标函数或约束条件为非线性的优化问题,常用于生产过程优化、风险管理等领域。
-
目标函数和约束:非线性规划的目标函数和约束可以是任意的非线性表达式。
-
局部最优解:非线性规划可能存在多个局部最优解,求解时需要考虑初始值的影响。
Matlab代码示例:非线性规划求解
% 定义目标函数
objFun = @(x) x(1)^2 + x(2)^2 + x(3)^2;% 定义非线性约束
nonlcon = @(xdeal) deal([], x(1)^2 + x(2)^2 - 1);% 使用fmincon函数求解非线性规划
x0 = [0.5, 0.5, 0.5];
[x, fval] = fmincon(objFun, x0, [], [], [], [], [], [], nonlcon);% 输出最优解和目标函数值
disp('最优解:');
disp(x);
disp('目标函数值:');
disp(fval);在该代码中,我们定义了一个非线性目标函数和约束条件,并使用fmincon函数求解了该非线性规划问题。
16.4 蒙特卡洛模拟
蒙特卡洛模拟是一种基于随机抽样的数值模拟方法,广泛用于风险分析和决策支持。通过多次随机抽样,蒙特卡洛模拟能够估计系统在不确定性条件下的行为。
-
随机抽样:通过对输入变量进行随机抽样,计算输出结果的统计特性。
-
应用场景:广泛应用于金融、工程可靠性、运营管理等领域。
Matlab代码示例:蒙特卡洛模拟计算圆周率
% 蒙特卡洛模拟计算圆周率
nPoints = 1e6; % 模拟点数
x = rand(nPoints, 1);
y = rand(nPoints, 1);% 计算落入圆内的点数
nInside = sum(x.^2 + y.^2 <= 1);% 估计圆周率
pi_estimate = 4 * nInside / nPoints;% 输出估计的圆周率
disp('估计的圆周率:');
disp(pi_estimate);在该代码中,我们使用蒙特卡洛模拟方法通过随机投点的方式计算了圆周率的近似值。
习题 16
在第十六章结束后,提供了一些相关的习题,帮助读者深入理解优化与模拟方法的应用。习题16包括:
线性规划:使用线性规划求解一个资源分配问题,找出最优分配方案。
整数规划:对一个设备选址问题建立整数规划模型,并求解最优选址方案。
非线性规划:建立一个生产优化模型,目标函数和约束条件为非线性,使用Matlab求解最优解。
蒙特卡洛模拟:使用蒙特卡洛模拟对投资组合的收益进行风险分析,估计收益的期望值和方差。
通过这些习题,读者可以进一步掌握优化与模拟方法在实际中的应用,以及如何利用Matlab工具进行复杂问题的建模与求解。
总结
第十六章介绍了优化与模拟方法的基本概念和常用方法,包括线性规划、整数规划、非线性规划和蒙特卡洛模拟等。优化方法帮助我们在复杂系统中找到最优方案,而模拟方法则通过随机抽样来理解系统在不确定条件下的行为。通过本章的学习,读者可以掌握这些方法的基本原理,并利用Matlab进行各种优化与模拟分析,从而为实际问题提供科学有效的解决方案。

相关文章:

数学建模算法与应用 第16章 优化与模拟方法
目录 16.1 线性规划 Matlab代码示例:线性规划求解 16.2 整数规划 Matlab代码示例:整数规划求解 16.3 非线性规划 Matlab代码示例:非线性规划求解 16.4 蒙特卡洛模拟 Matlab代码示例:蒙特卡洛模拟计算圆周率 习题 16 总结…...
windows下安装、配置neo4j并服务化启动
第一步:下载Neo4j压缩包 官网下载地址:https://neo4j.com/download-center/ (官网下载真的非常慢,而且会自己中断,建议从以下链接下载) 百度网盘下载地址:链接:https://pan.baid…...

【JVM】—深入理解G1回收器—回收过程详解
深入理解G1回收器—回收过程详解 ⭐⭐⭐⭐⭐⭐ Github主页👉https://github.com/A-BigTree 笔记链接👉https://github.com/A-BigTree/Code_Learning ⭐⭐⭐⭐⭐⭐ 如果可以,麻烦各位看官顺手点个star~😊 文章目录 深入理解G1回收…...

2、CSS笔记
文章目录 二、CSS基础CSS简介CSS语法规范CSS代码风格CSS选择器CSS基础选择器标签选择器类选择器--最常用id选择器通配符选择器 CSS复合选择器交集选择器--重要并集选择器--重要后代选择器--最常用子代选择器--重要兄弟选择器相邻兄弟选择器通用兄弟选择器 属性选择器伪类选择器…...

使用XML实现MyBatis的基础操作
目录 前言 1.准备工作 1.1⽂件配置 1.2添加 mapper 接⼝ 2.增删改查操作 2.1增(Insert) 2.2删(Delete) 2.3改(Update) 2.4查(Select) 前言 接下来我们会使用的数据表如下: 对应的实体类为:UserInfo 所有的准备工作都在如下文章。 MyBatis 操作…...

智汇云舟亮相WAFI世界农业科技创新大会,并参编数字农业产业图谱
10月10日,2024WAFI世界农业科技创新大会农食行业创新与投资峰会在北京金海湖国际会展中心举行。中国农业大学MBA教育中心主任、教授付文阁、平谷区委常委、统战部部长刘堃、华为公共事业军团数字政府首席专家刘丹、荷兰瓦赫宁根大学前校长Aalt Dijkhuizen、牧原食品…...

昇思MindSpore进阶教程--数据处理性能优化(中)
大家好,我是刘明,明志科技创始人,华为昇思MindSpore布道师。 技术上主攻前端开发、鸿蒙开发和AI算法研究。 努力为大家带来持续的技术分享,如果你也喜欢我的文章,就点个关注吧 shuffle性能优化 shuffle操作主要是对有…...

Vivado - Aurora 8B/10B IP
目录 1. 简介 2. 设计调试 2.1 Physical Layer 2.2 Link Layer 2.3 Receiver 2.4 IP 接口 2.5 调试过程 2.5.1 Block Design 2.5.2 释放 gt_reset 2.5.3 观察数据 3. 实用技巧 3.1 GT 坐标与布局 3.1.1 选择器件并进行RTL分析 3.1.2 进入平面设计 3.1.3 收发器布…...

图(Java语言实现)
一、图的概念 顶点(Vertex):图中的数据元素,我们称之为顶点,图至少有一个顶点(非空有穷集合)。 边(Edge):顶点之间的关系用边表示。 1.图(Graph…...

GPT 生成绘画_Java语言例子_超详细
基于spring ai :简化Java AI开发,提升效率与维护性 过去在使用Java编写AI应用时,主要困境在于缺乏统一的标准化封装,开发者需要针对不同的AI服务提供商查阅各自独立的文档并进行接口对接,这不仅增加了开发的工作量&am…...

华为OD机试 - 小朋友分组最少调整次数 - 贪心算法(Python/JS/C/C++ 2024 E卷 100分)
华为OD机试 2024E卷题库疯狂收录中,刷题点这里 专栏导读 本专栏收录于《华为OD机试真题(Python/JS/C/C)》。 刷的越多,抽中的概率越大,私信哪吒,备注华为OD,加入华为OD刷题交流群,…...
数字农业与遥感监测平台
随着全球人口的增长和气候变化的挑战,农业的可持续发展变得尤为重要。数字农业作为现代农业发展的重要方向,正逐渐成为提高农业生产效率、保障粮食安全的关键手段。遥感技术作为数字农业的重要组成部分,通过监测作物生长状况、土壤湿度、病虫…...

2023年12月中国电子学会青少年软件编程(Python)等级考试试卷(一级)答案 + 解析
一、单选题 1、下列程序运行的结果是?( ) print(hello) print(world) A.helloworld B.hello world C.hello world D.helloworld 正确答案:B 答案解析:本题考察的 Python 编程基础,print 在打印时…...

【优选算法】——双指针(下篇)!
🌈个人主页:秋风起,再归来~ 🔥系列专栏:C刷题算法总结 🔖克心守己,律己则安 目录 1、有效三角形的个数 2、查找总价值为目标值的两个商品 3、三数之和 4、四数之和 5、完结散花 1、有…...

C#中函数重载的说明
一.函数重载的基本概念 C# 中的函数重载是指在同一个类中定义多个同名的函数,但这些函数的参数类型、参数个数、参数顺序等不同,以便适应不同的调用需求,增加代码的兼容性。 二.函数重载的作用 2.1定义多个相类似的函数,减少函…...
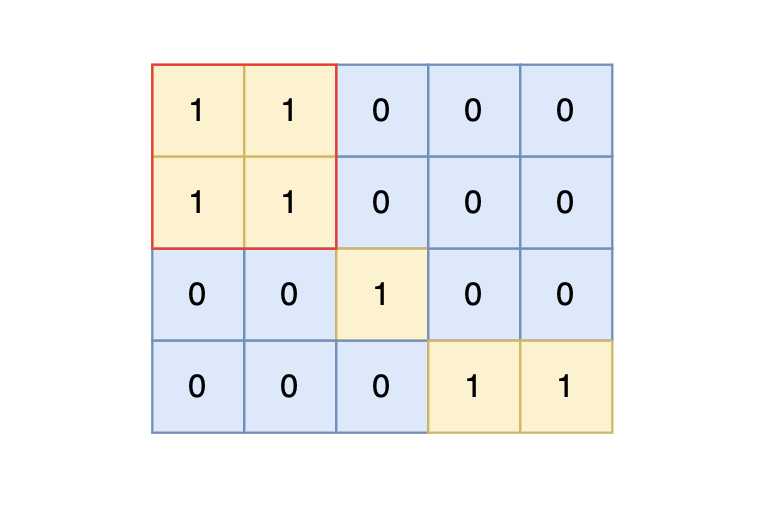
图论day56|广度优先搜索理论基础 、bfs与dfs的对比(思维导图)、 99.岛屿数量(卡码网)、100.岛屿的最大面积(卡码网)
图论day56|广度优先搜索理论基础 、bfs与dfs的对比(思维导图)、 99.岛屿数量(卡码网)、100.岛屿的最大面积(卡码网)) 广度优先搜索理论基础bfs与dfs的对比(思维导图)&…...

源码编译方式安装htppd软件
一.源码编译安装httpd软件 1.安装阿帕奇的依赖,安装apr软件,阿帕奇正常运行的环境这个环境就是apr。 2.安装apr-util软件,主要提供针对apr环境的管理工具, 3.安装阿帕奇软件即httpd软件。 如上图所示,就是三个软件的…...

MES制造执行系统原型图动端 Axure原型 交互设计 Axure实战项目
MES制造执行系统原型移动端 Manufacturing Execution System prototype MES制造执行系统原型图移动端是专门为制造执行系统设计的移动端是一个可视化的设计。用于展示和演示该系统在移动设备上的功能和界面。通过原型图,可以清晰地了解制造执行系统在移动端的各个…...

flutter 仿淘宝推荐二级分类效果
先看效果 一开始 用的PageView 做的, 然后重写PageScrollPhysics一顿魔改, 最后发现还是有一些小bug。 后面又想到pageview 能做,listview肯定也能做,最后用ListView加GridView 把功能实现了。 listview 实现pageview 的分页滑动…...

报错 - LangChain AgentExecutor - ‘function‘ object has no attribute ‘get‘
使用 AgentExecutor 调用了使用两个 tool 的agent,报一下错误: 如果 agent 只使用 一个tool,没有报错 File "/Users/xx/miniconda3/envs/env1/lib/python3.11/site-packages/pydantic/_internal/_validators.py", line 44, in sequ…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...

SpringTask-03.入门案例
一.入门案例 启动类: package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...

Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决
Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决 问题背景 在一个基于 Spring Cloud Gateway WebFlux 构建的微服务项目中,新增了一个本地验证码接口 /code,使用函数式路由(RouterFunction)和 Hutool 的 Circle…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信
文章目录 Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信前言一、网络通信基础概念二、服务端与客户端的完整流程图解三、每一步的详细讲解和代码示例1. 创建Socket(服务端和客户端都要)2. 绑定本地地址和端口&#x…...
