PDF 转 CAD 工具:实现文档格式高效转换的利器
如果你从事设计相关PDF和CAD作为两种常见且重要的文件格式,在不同的领域都有着广泛的应用。今天,我们就来介绍几个各具特色的PDF转换成CAD工具。
1.福昕PDF转换大师
链接一下>>https://www.pdf365.cn/pdf2word/
该工具在跨领域应用中表现出明确的功能性与直观简洁的操作界面,显著提高了我们的转换效率。它不仅能够灵活地将PDF文件转换成多种其他格式,还能轻松地将其他格式的文件转换为PDF,充分满足了用户多样化的文件转换需求。
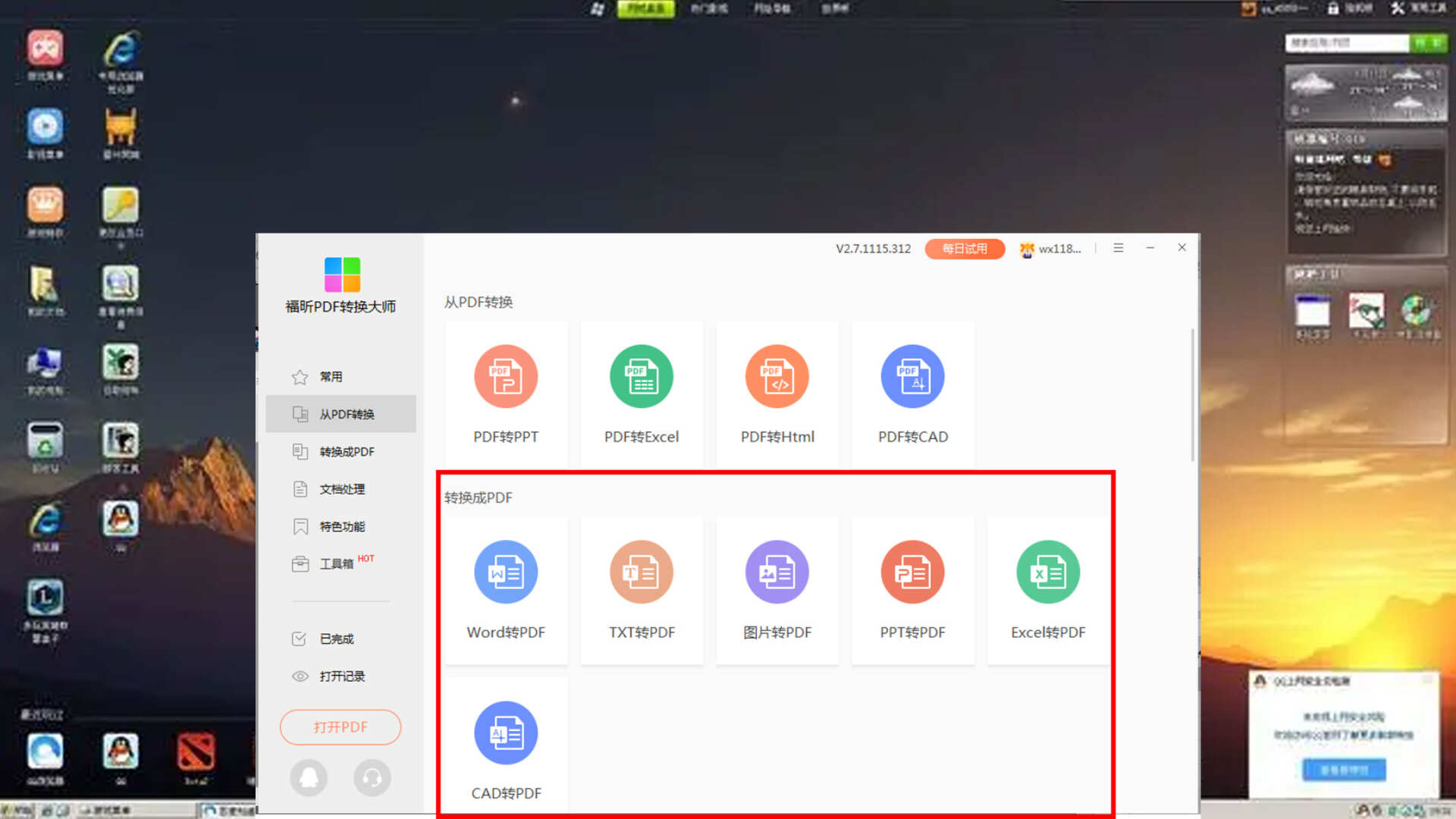
在软件的操作界面左侧,用户可以轻松找到“PDF转换”这一功能模块。进一步浏览至界面右侧,用户会惊喜地发现专门设置的“CAD转PDF”功能按钮。用户只需进入新的操作界面,上传待转换的CAD文件,设定好所需的导出参数,最后点击转换按钮,软件就能在极短的时间内高效完成转换任务。

2.PDF365在线转换
链接一下>>https://www.pdf365.cn/
这个网站是解决我们日常PDF文件处理难题的得力助手,尤其适合那些不想安装额外软件的用户,不妨将其加入收藏以备不时之需。它提供了丰富的功能,包括PDF格式转换、音频视频简单编辑,以及从图片、视频、音频中提取文字等,实用性极强。
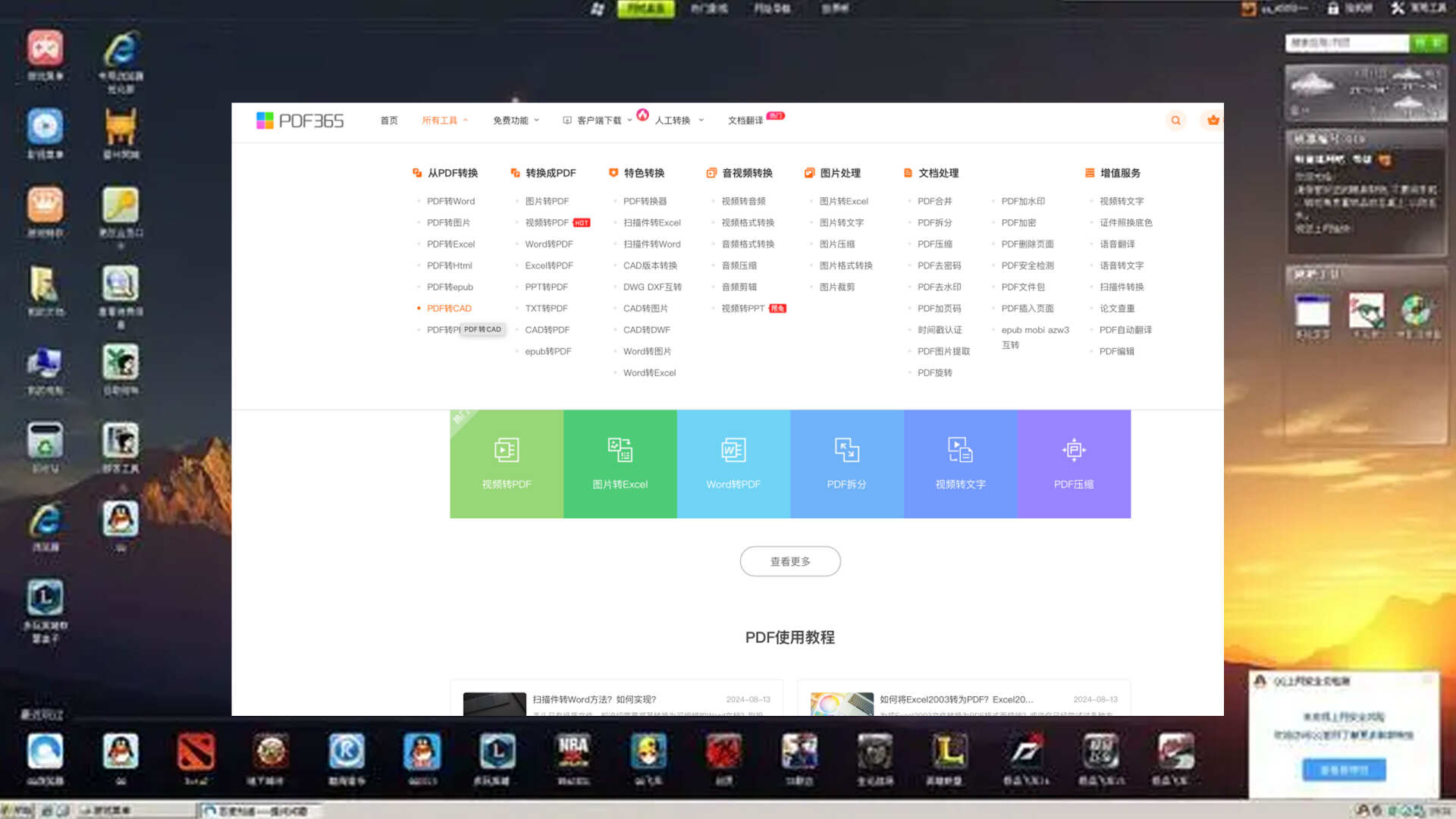
访问该网站后,只需在顶部导航栏的“所有工具”下拉菜单中轻松找到“CAD转PDF”选项。进入新界面后,用户只需在指定区域上传需要转换为PDF格式的CAD文件;待网站处理完毕后,即可下载转换后的PDF文件,从而轻松获得可编辑的CAD图纸。

3.福昕PDF编辑转换
链接一下>>https://editor.foxitsoftware.cn
这是一款专业的PDF编辑软件,能够全面支持对PDF文件的各类编辑操作,如增减内容、页面,设置权限及添加水印等,均能轻松应对。此外,它还广泛支持PDF文件与其他多种文件格式之间的转换。
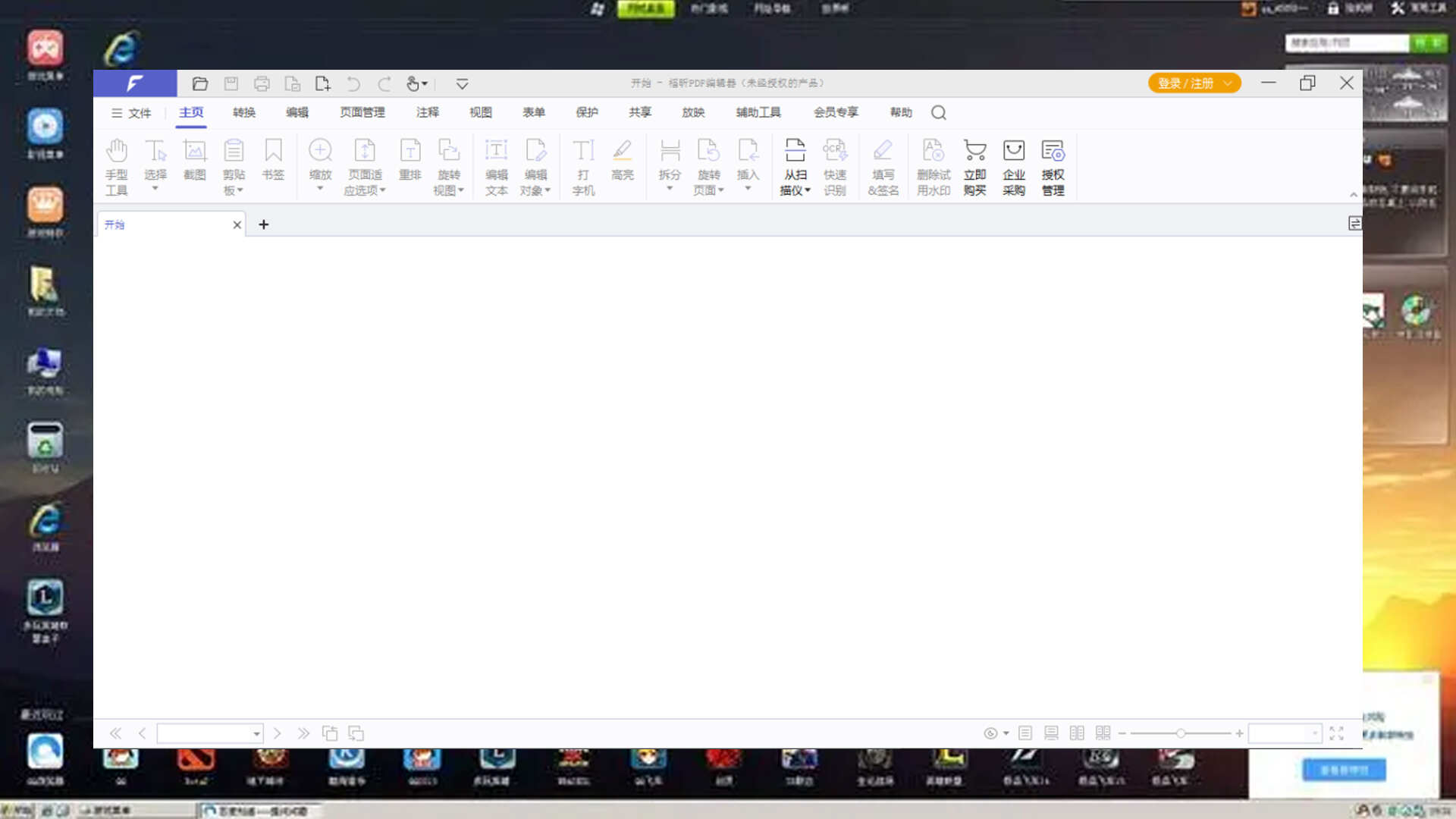
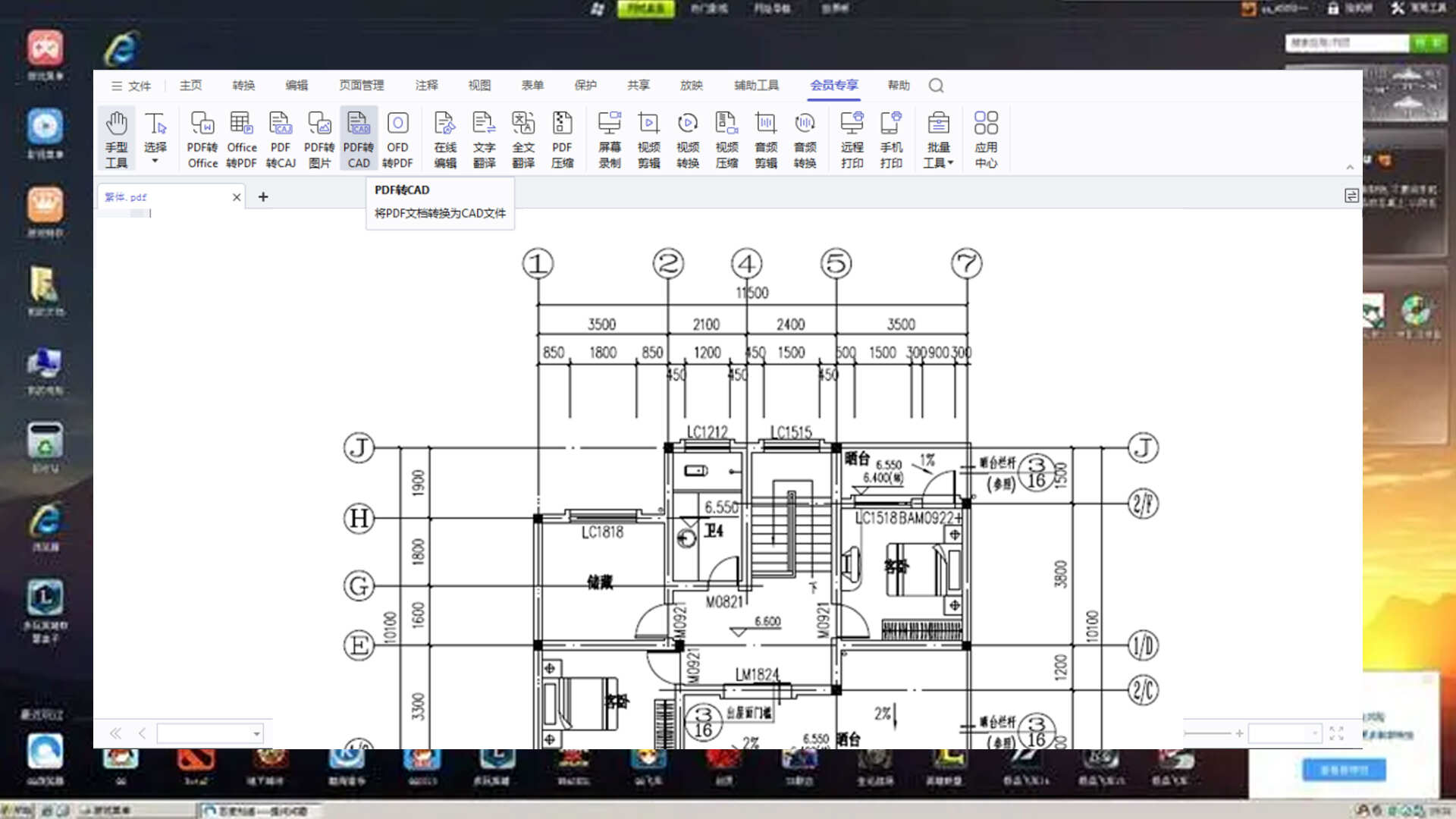
使用该软件打开PDF文件后,用户可在顶部的“会员专享”菜单下找到“PDF转CAD”的功能按钮。点击后,即可遵循界面提供的指引,将PDF图纸转换为CAD相关格式。在转换过程中,用户还可以根据界面窗口的提示,灵活设置图纸的尺寸、格式以及适配的软件版本等参数,从而确保转换出的建筑图纸更加贴合实际需求。
4.zamzar
链接一下>>www.zamzar.com/converters/cad/
这个工具是一个在线平台,因此无需下载,仅需通过网络即可便捷使用。其核心功能主要集中在与CAD相关的格式转换上。使用时,我们只需简单地上传PDF文件,选定CAD作为目标格式,然后耐心等待转换过程的完成。一旦转换完毕,您将会收到一封包含转换后CAD文件的电子邮件,只需查收邮件即可轻松获取所需文件。
这些不同的PDF转换成CAD工具都在各自的领域发挥着重要作用。它们以独特的功能和特点,满足了不同用户的需求。无论是对于专业的设计师,还是相关行业的从业者,都能从这些工具中找到适合自己的解决方案。
相关文章:

PDF 转 CAD 工具:实现文档格式高效转换的利器
如果你从事设计相关PDF和CAD作为两种常见且重要的文件格式,在不同的领域都有着广泛的应用。今天,我们就来介绍几个各具特色的PDF转换成CAD工具。 1.福昕PDF转换大师 链接一下>>https://www.pdf365.cn/pdf2word/ 该工具在跨领域应用中表现出明确…...

基于springboot的画师约稿系统的设计与实现
文章目录 项目介绍主要功能截图:部分代码展示设计总结项目获取方式🍅 作者主页:超级无敌暴龙战士塔塔开 🍅 简介:Java领域优质创作者🏆、 简历模板、学习资料、面试题库【关注我,都给你】 🍅文末获取源码联系🍅 项目介绍 基于springboot的画师约稿系统的设计与实…...

使用Python生成SVG图片
SVG(可缩放矢量图形)是一种基于XML的图像格式,它可以无损缩放且文件大小较小。在本文中,我们将探讨如何使用Python生成SVG图片。 为什么选择SVG? 可缩放:SVG图像可以无限放大而不失真。文件小:SVG文件通常比位图文件小。可编辑:SVG文件可以通过文本编辑器修改。 使用Python…...

hackmyvm-Hundred靶机
主机发现 sudo arp-scan -l 以sudo权限执行arp-scan -l 扫描并列出本地存在的机器,发现靶机ip为192.168.91.153 nmap扫描 端口发现 21/tcp open ftp 22/tcp open ssh 80/tcp open http web信息收集 我们先尝试一下ftp端口的匿名登录 FTP:是文件传输协议的端…...

多场景多任务建模(三): M2M(Multi-Scenario Multi-Task Meta Learning)
多场景建模: STAR(Star Topology Adaptive Recommender) 多场景建模(二): SAR-Net(Scenario-Aware Ranking Network) 前面两篇文章,讲述了关于多场景的建模方案,其中可以看到很多关于多任务学习的影子&…...

Day31 || 122.买卖股票的最佳时机 II、55. 跳跃游戏、 45.跳跃游戏II 、1005.K次取反后最大化的数组和
122.买卖股票的最佳时机 II 题目链接:力扣题目链接 思路:因为是求虽大利润完全可以假设知道第二天涨前一天买入即可,就是求两天只差大于0 的和。 55. 跳跃游戏 题目链接:力扣题目链接 思路:应该从后往前循环判断&…...

【uniapp】打包成H5并发布
目录 1、设置配置mainifest.sjon 1.1 页面标题 1.2 路由模式 1.3 运行的基础路径 2、打包 2.1 打包入口 2.2 打包成功 2.3 依据目录找到web目录 3、 将web目录整体拷贝出来 4、上传 4.1 登录uniapp官网注册免费空间 4.2 上传拷贝的目录 4.3 检查上传是否正确 5、…...

Position Embedding总结和Pytorch实现
文章目录 出现背景PE位置编码公式思路code 出现背景 自注意力机制处理数据,并不是采用类似RNN或者LSTM那种递归的结构,这使得模型虽然能够同时查看输入序列中的所有元素(即并行运算),但是也导致了没办法获取当前word在…...
【AIF-C01认证】亚马逊云科技生成式 AI 认证正式上线啦
文章目录 一、AIF-C01简介二、考试概览三、考试知识点3.1 AI 和 ML 基础知识3.2 生成式人工智能基础3.3 基础模型的应用3.4 负责任 AI 准则3.5 AI 解决方案的安全性、合规性和监管 四、备考课程4.1 「备考训练营」 在线直播课4.2 「SkillBuilder」学习课程 五、常见问题六、参考…...

C++ 素数的筛选法与穷举法
题目:素数大酬宾: 【问题描述】 某商场的仓库中有 n 种商品,每件商品按 1~n 依次编号。现在商场经理突发奇想,决定将编号为素数(质数)的所有商品拿出来搞优惠酬宾活动。请编程帮助仓库管理员将编号为素数的商品选出来…...

Spring Boot异步任务、任务调度与异步请求线程池的使用及原理
Spring Boot异步任务、任务调度与异步请求线程池的使用及原理 在Spring Boot应用程序中,异步任务、任务调度和异步请求线程池是提高系统性能和响应速度的重要工具。本文将详细讲解这些概念的使用及原理。 一、异步任务 异步任务是指可以在后台线程上执行的任务&a…...

Java爬虫之使用Selenium WebDriver 爬取数据
这里写自定义目录标题 Selenium WebDriver简介一、安装部署二、Java项目中使用1.引入依赖2.示例代码 三、WebDriver使用说明1.WebDriver定位器2.常用操作3.使用 cookie4.键盘与鼠标操作 Selenium WebDriver简介 Selenium WebDriver 是一种用于自动化测试 Web 应用程序的工具。…...

MyBatis 中updateByPrimaryKey和updateByPrimaryKeySelective区别
在 MyBatis 中,updateByPrimaryKey和updateByPrimaryKeySelective主要有以下区别: 一、功能 updateByPrimaryKey: 会根据传入的实体对象,将数据库表中对应主键的记录所有字段全部更新为实体对象中的值。即使实体对象中的某些字段…...

JavaScript下载文件(简单模式、跨域问题、文件压缩)
文章目录 简介简单文件下载通过模拟form表单提交通过XMLHttpRequest方式 跨域(oss)下载并压缩文件完整示例文件压缩跨域设置 简介 相信各位开发朋友都遇到过下载的文件的需求,有的非常简单,基本链接的形式就可以。 有的就比较复杂,涉及跨域…...

Django 定义使用模型,并添加数据
教材: Python web企业级项目开发教程(黑马程序员)第三章 模型 实验步骤: 1.创建项目和应用 前置步骤可看前文,进入到指定文件位置后创建 django-admin startproject mysite python manage.py startapp app01 2.注册…...
联名物料常泄漏?一端叠满“安全buff”
前段时间,一则关于爆火影视剧与知名茶饮品牌联名的消息在社交平台上迅速传播,宣传物料的照片也随之曝光——门店尚未上新,“小道消息”便已被疯传。但这种情况并非首次发生,让众多网友不禁猜想:这究竟是一场精心策划的…...

Flutter UI组件库(JUI)
Flutter UI组件库 (JUI) 介绍 您是否正在寻找一种方法来简化Flutter开发过程,并创建美观、一致的用户界面?您的搜索到此为止!我们的Flutter UI组件库(JUI)提供了广泛的预构建、可自定义组件,帮助您快速构建…...

国外电商系统开发-运维系统远程文件
设计初衷是为了让所有人都能方便的打开网页,就能查看Linux系统文件内容,而不再用cat、vim、more等命令去打开文件,这对于我们一个普通的研发或者是财务人员来说,显得太繁琐,因为他们很可能不会这些命令,其次…...

4. Node.js Path模块
2.3Path模块 2.3.1获取js文件的绝对路径 console.log(__dirname) //js文件所在的文件夹的绝对路径 console.log(__filename) //js文件的绝对路径输出: G:\py_project\nodejs_study G:\py_project\nodejs_study\file.js2.3.2拼接规范的绝对路径path.r…...

重构长方法之分解条件表达式
分解条件表达式 是一种重构长方法中常用的技术,它适用于复杂的条件逻辑。在方法中,条件分支(if-else 或 switch)有时会变得条件非常多,非常复杂,难以理解和维护。通过分解条件逻辑,可以让代码更…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

【笔记】WSL 中 Rust 安装与测试完整记录
#工作记录 WSL 中 Rust 安装与测试完整记录 1. 运行环境 系统:Ubuntu 24.04 LTS (WSL2)架构:x86_64 (GNU/Linux)Rust 版本:rustc 1.87.0 (2025-05-09)Cargo 版本:cargo 1.87.0 (2025-05-06) 2. 安装 Rust 2.1 使用 Rust 官方安…...

【Linux】自动化构建-Make/Makefile
前言 上文我们讲到了Linux中的编译器gcc/g 【Linux】编译器gcc/g及其库的详细介绍-CSDN博客 本来我们将一个对于编译来说很重要的工具:make/makfile 1.背景 在一个工程中源文件不计其数,其按类型、功能、模块分别放在若干个目录中,mak…...

图解JavaScript原型:原型链及其分析 | JavaScript图解
忽略该图的细节(如内存地址值没有用二进制) 以下是对该图进一步的理解和总结 1. JS 对象概念的辨析 对象是什么:保存在堆中一块区域,同时在栈中有一块区域保存其在堆中的地址(也就是我们通常说的该变量指向谁&…...

Java并发编程实战 Day 11:并发设计模式
【Java并发编程实战 Day 11】并发设计模式 开篇 这是"Java并发编程实战"系列的第11天,今天我们聚焦于并发设计模式。并发设计模式是解决多线程环境下常见问题的经典解决方案,它们不仅提供了优雅的设计思路,还能显著提升系统的性能…...
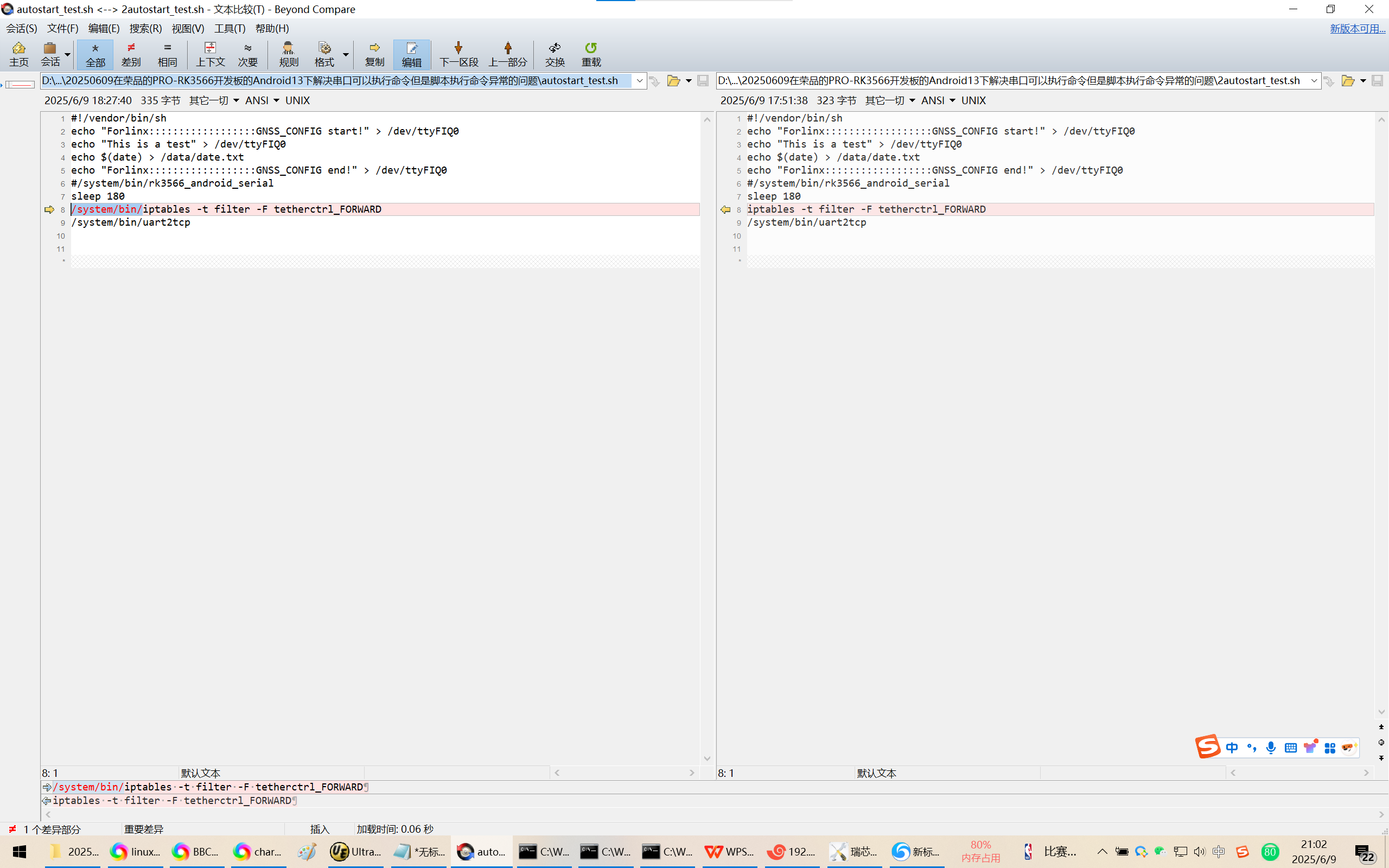
20250609在荣品的PRO-RK3566开发板的Android13下解决串口可以执行命令但是脚本执行命令异常的问题
20250609在荣品的PRO-RK3566开发板的Android13下解决串口可以执行命令但是脚本执行命令异常的问题 2025/6/9 20:54 缘起,为了跨网段推流,千辛万苦配置好了网络参数。 但是命令iptables -t filter -F tetherctrl_FORWARD可以在调试串口/DEBUG口正确执行。…...
