【C++刷题】力扣-#118-杨辉三角
题目描述
给定一个非负整数 numRows,生成杨辉三角的前 numRows 行。在杨辉三角中,每个数是它正上方两个数的和。
示例
示例 1:
输入: numRows = 5
输出: [[1],[1,1],[1,2,1],[1,3,3,1],[1,4,6,4,1]]
示例 2:
输入: numRows = 1
输出: [[1]]
题解
这个问题可以通过动态规划来解决。我们可以使用一个二维数组来存储杨辉三角的每一行,然后根据上一行计算下一行的值。
- 初始化:创建一个空列表 triangle 来存储杨辉三角的每一行。
- 特殊情况:如果 numRows 为 0,返回空列表;如果 numRows 为 1,返回只有一个元素 [1] 的列表。
- 构建杨辉三角:对于每一行 i(从 0 到 numRows - 1):
○ 创建一个列表 row,初始值为 [1],因为每一行的第一个和最后一个数字都是 1。
○ 如果当前行不是第一行,对于 row 中的每个位置 j(从 1 到 i - 1),计算 row[j] 的值为 triangle[i - 1][j - 1] + triangle[i - 1][j]。
○ 将计算好的行添加到 triangle 中。 - 返回结果:返回 triangle。
代码实现
vector<vector<int>> generate(int numRows) {vector<vector<int>> triangle;for (int i = 0; i < numRows; i++) {std::vector<int> row(i + 1, 1); // 初始化行,首尾为1if (i > 0) {for (int j = 1; j < i; j++) {row[j] = triangle[i - 1][j - 1] + triangle[i - 1][j];}}triangle.push_back(row);}return triangle;
}
复杂度分析
● 时间复杂度:O(numRows^2),因为我们需要计算每一行的每个数字,每个数字的计算时间是 O(1)。
● 空间复杂度:O(numRows^2),因为我们需要存储整个杨辉三角的前 numRows 行。
这个算法的优势在于它直接模拟了杨辉三角的构建过程,不需要额外的数学计算。
相关文章:

【C++刷题】力扣-#118-杨辉三角
题目描述 给定一个非负整数 numRows,生成杨辉三角的前 numRows 行。在杨辉三角中,每个数是它正上方两个数的和。 示例 示例 1: 输入: numRows 5 输出: [[1],[1,1],[1,2,1],[1,3,3,1],[1,4,6,4,1]]示例 2: 输入: numRows 1 输出: [[1]]题解 这个问题…...

Linux下的环境变量
目录 1.引言 1.1bash的部分工作 1.2main函数也有参数 1.3我们可以通过给main函数传入不同的参数,让同一份代码实现不同的功能 1.4先认识一个环境变量PATH,帮助Linux找到指令程序的地址 2.环境变量 2.1环境变量的概念 2.2见见其他的环境变量 2…...

Edge论文的创新点
创新点及其来源 1. 从灰度边缘重建RGB图像的方法(EdgRec) 基于的方法:传统的重建方法,如使用自动编码器或生成模型来重建正常样本的图像,并通过对原始图像和重建图像的比较来检测异常。 重建过程: 训练阶…...
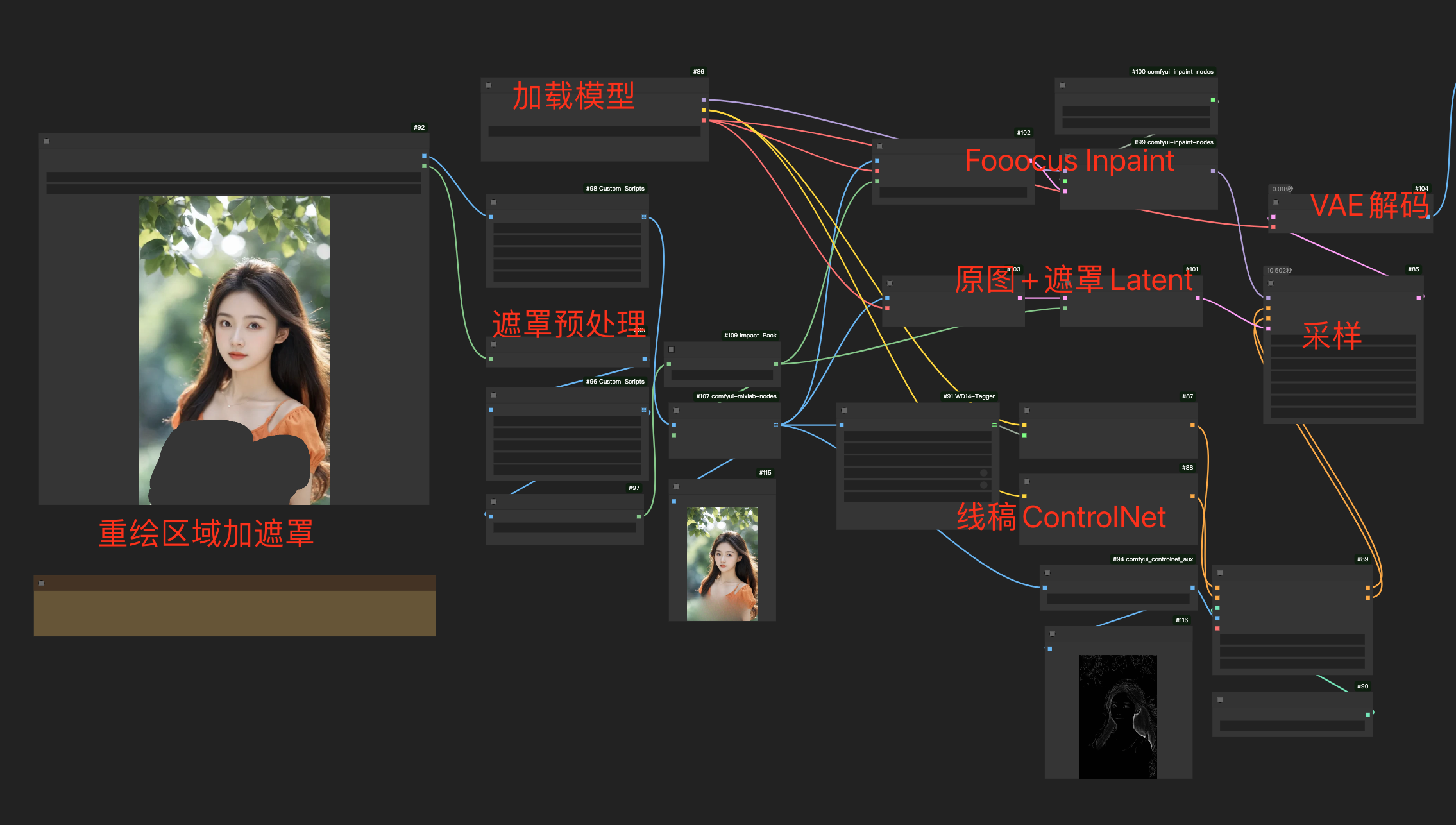
ComfyUI 高级实战:实现华为手机的AI消除功能
大家好,我是每天分享AI应用的萤火君! 不知道大家是否还记得华为 Pura 70的「AI消除」事件,当时使用 华为Pura 70 系列手机的智能消除功能时,该功能可以被用来消除照片中女性胸口处的衣物,这一功能曾引发广泛的关注和伦…...

我记得我曾喜欢过冬天
写在前面 1316 字 | 感触 | 世界 | 情感 | 体验 | 经历 | 想法 | 认知 正文 晚上出门,起电单车,很冷。冻得有些发抖。下车,我第一时间和珍发了消息。 我说,居然在四川感受到了哈尔滨的温度。 哈尔滨的夏天很热,但哈尔…...
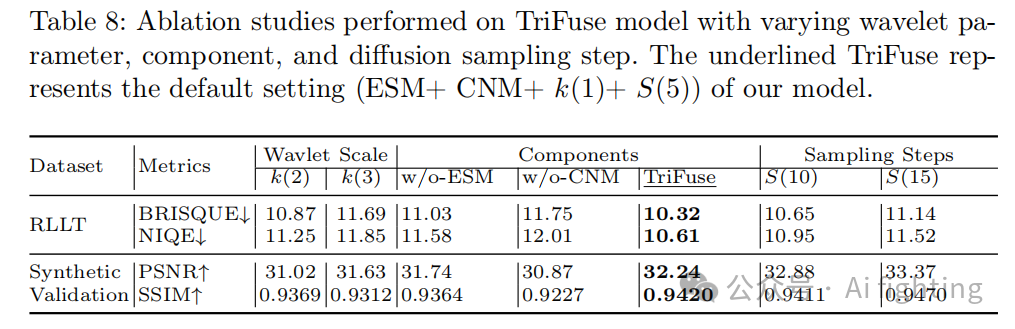
最新夜间数据集发布LoLI-Street: 33000帧数据,涵盖19000个目标
最新夜间数据集发布LoLI-Street: 33000帧数据,涵盖19000个目标 Abstract 低光照图像增强(LLIE)对于许多计算机视觉任务至关重要,包括目标检测、跟踪、分割和场景理解。尽管已有大量研究致力于提高在低光照条件下捕捉的低质量图像…...

反向传播算法与随机搜索算法的比较
反向传播算法与随机搜索算法的比较 在这篇文章中,我们将通过一个简单的线性回归问题来比较反向传播算法和随机搜索算法的性能。我们将使用Python代码来实现这两种算法,并可视化它们的梯度下降过程。 反向传播算法 反向传播算法是深度学习和神经网络训…...

【PDF文件】默认被某种软件打开,如何进行修改?
当有时下载某种软件后,电脑中的PDF文件就默认由该种软件打开,每次需要右键选择打开方式才能选择需要的其他软件打开。如下图所示。 修改方法: (1)点击电脑的“设置”,选择应用 (2)…...

Kaggle Python练习:字符串和字典(Exercise: Strings and Dictionaries)
文章目录 问题:搜索特定单词并定位思路代码实现官方代码代码解析 更进一步 问题:搜索特定单词并定位 一位研究人员收集了数千篇新闻文章。但她想将注意力集中在包含特定单词的文章上。完成以下功能以帮助她过滤文章列表。 您的函数应满足以下条件&…...

React(四) 事件总线,setState的原理,PureComponent优化React性能,ref获取类组件与函数组件
文章目录 一、全局事件总线二、setState的原理1. 为什么要使用setState修改数据2. setState的三种用法(1) 基本使用(2) 传入回调函数(3) setState是一个异步调用 3. setState为什么要设置成异步 二、PureComponent优化性能1. React的diff算法以及Key的优化(扩展)(1) diff算法(2…...
Java学习-JVM
目录 1. 基本常识 1.1 JVM是什么 1.2 JVM架构图 1.3 Java技术体系 1.4 Java与JVM的关系 2. 类加载系统 2.1 类加载器种类 2.2 执行顺序 2.3 类加载四个时机 2.4 生命周期 2.5 类加载途径 2.6 双亲委派模型 3. 运行时数据区 3.1 运行时数据区构成 3.2 堆 3.3 栈…...

leed认证分几个级别
LEED(Leadership in Energy and Environmental Design)认证是一个评估建筑项目可持续性的严格框架,其级别主要分为以下四个: LEED认证(Certified):这是最低级别的认证,要求建筑项目…...

3.C++经典实例-计算一个数的阶乘
阶乘(factorial)是基斯顿卡曼于1808年发明的运算符号,用于表示一个正整数n的所有小于及等于该数的正整数的积。自然数n的阶乘写作n!。例如,5的阶乘表示为5! 1 2 3 4 5 120。 阶乘在数学和计算机科学中有广泛的应用。例如…...

深入理解Qt中的QTableView、Model与Delegate机制
文章目录 显示效果QTableViewModel(模型)Delegate(委托)ITEM控件主函数调用项目下载在Qt中,视图(View)、模型(Model)和委托(Delegate)机制是一种非常强大的架构,它们实现了MVC(模型-视图-控制器)设计模式。这种架构分离了数据存储(模型)、数据展示(视图)和数据操作(委托),使…...

解读《ARM Cortex-M3 与Cortex-M4 权威指南》——第1章 ARM Cortex-M处理器简介
1. 三级流水线设计 解释:三级流水线设计意味着处理器在执行指令时可以同时处理多个步骤。这些步骤通常包括取指(Fetch)、译码(Decode)和执行(Execute)。好处:这种设计提高了指令的执行效率,使得处理器能够在每个时钟周期内完成更多的工作,从而提升整体性能。2. 哈佛总…...

java集合类的框架体系
1.集合的好处 相比数组,他可以存储多种类型的元素,并且可以动态新增; 2. 集合分类 3.Collection接口 3.1常用方法 3.2迭代器-遍历 collection接口继承了Interable接口,collection的子类可以使用迭代器; 注意事项…...
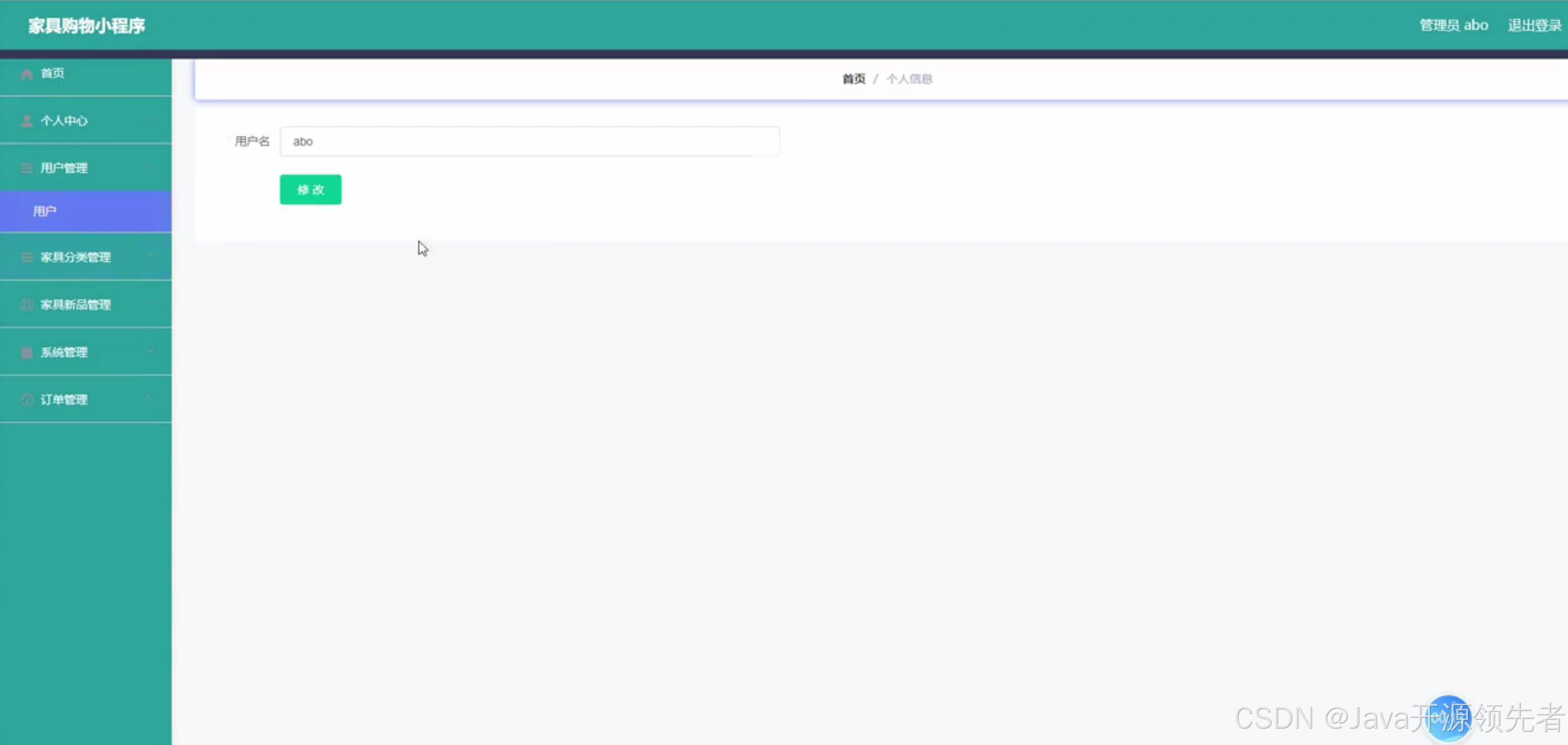
基于SpringBoot+Vue+Uniapp家具购物小程序的设计与实现
详细视频演示 请联系我获取更详细的演示视频 项目运行截图 技术框架 后端采用SpringBoot框架 Spring Boot 是一个用于快速开发基于 Spring 框架的应用程序的开源框架。它采用约定大于配置的理念,提供了一套默认的配置,让开发者可以更专注于业务逻辑而…...

什么是模糊测试?
近年来,随着信息技术的发展,各种新型自动化测试技术如雨后春笋般出现。其中,模糊测试(fuzz testing)技术开始受到行业关注,它尤其适用于发现未知的、隐蔽性较强的底层缺陷。这里,我们将结合AFL开…...

3.C++经典实例-奇数还是偶数
要判断一个数是奇数还是偶数,只需要判断这个数是否能被2整除即可,如果要判断是否能整除,则要判断当前数除以2的余数是否为0,在C中,余数,使用%号,因此,程序为: #include …...
真牛啊!全球人工智能标准教科书,斯坦福、麻省理工、加州大学等十多所顶尖机构为它点赞!!
这本《人工智能:计算代理基础》堪称全球人工智能标准教科书!它因其前沿的技术融合、丰富的实践案例以及理论深度与实践并重的特点而成为人工智能领域的热门书籍。 该书已经赢得了斯坦福大学、佐治亚理工学院、谷歌大脑、麻省理工学院、加州大学、微软研究…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建: 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建: File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...
