2010年国赛高教杯数学建模C题输油管的布置解题全过程文档及程序
2010年国赛高教杯数学建模
C题 输油管的布置
某油田计划在铁路线一侧建造两家炼油厂,同时在铁路线上增建一个车站,用来运送成品油。由于这种模式具有一定的普遍性,油田设计院希望建立管线建设费用最省的一般数学模型与方法。
1. 针对两炼油厂到铁路线距离和两炼油厂间距离的各种不同情形,提出你的设计方案。在方案设计时,若有共用管线,应考虑共用管线费用与非共用管线费用相同或不同的情形。
2. 设计院目前需对一更为复杂的情形进行具体的设计。两炼油厂的具体位置由附图所示,其中A厂位于郊区(图中的I区域),B厂位于城区(图中的II区域),两个区域的分界线用图中的虚线表示。图中各字母表示的距离(单位:千米)分别为a = 5,b = 8,c = 15,l = 20。

若所有管线的铺设费用均为每千米7.2万元。 铺设在城区的管线还需增加拆迁和工程补偿等附加费用,为对此项附加费用进行估计,聘请三家工程咨询公司(其中公司一具有甲级资质,公司二和公司三具有乙级资质)进行了估算。估算结果如下表所示:

请为设计院给出管线布置方案及相应的费用。
3. 在该实际问题中,为进一步节省费用,可以根据炼油厂的生产能力,选用相适应的油管。这时的管线铺设费用将分别降为输送A厂成品油的每千米5.6万元,输送B厂成品油的每千米6.0万元,共用管线费用为每千米7.2万元,拆迁等附加费用同上。请给出管线最佳布置方案及相应的费用。
整体求解过程概述(摘要)
“输油管的布置”数学建模的目的是设计最优化的路线,建立一条费用最省的输油管线路,但是不同于普遍的最短路径问题,该题需要考虑多种情况,例如,城区和郊区费用的不同,采用共用管线和非公用管线价格的不同等等。我们基于最短路径模型,对于题目实际情况进行研究和分析,对三个问题都设计了合适的数学模型做出了相应的解答和处理。
问题一:此问只需考虑两个加油站和铁路之间位置的关系,根据位置的不同设计相应的模型,我们基于光的传播原理,设计了一种改进的最短路径模型,在不考虑共用管线价格差异的情况下,只考虑如何设计最短的路线,因此只需一个未知变量便可以列出最短路径函数;在考虑到共用管线价格差异的情况下,则需要建立2个未知变量,如果带入已知常量,可以解出变量的值。
问题二:此问给出了两个加油站的具体位置,并且增加了城区和郊区的特殊情况,我们进一步改进数学模型,将输油管路线横跨两个不同的区域考虑为光在两种不同介质中传播的情况,输油管在城区和郊区的铺设将不会是直线方式,我们将其考虑为光在不同介质中传播发生了折射。在郊区的路线依然可以采用问题一的改进最短路径模型,基于该模型,我们只需设计2个变量就可以列出最低费用函数,利用Matlab和VC++ 都可以解出最小值,并且我们经过多次验证和求解,将路径精度控制到米,费用精度控制到元。
问题三:该问的解答方法和问题二类似,但是由于A管线、B管线、共用管线三者的价格均不一样,我们利用问题二中设计的数学模型,以铁路为横坐标,城郊交汇为纵坐标建立坐标轴,增加了一个变量,建立了最低费用函数,并且利用VC++解出了最低费用和路径坐标。
模型假设:
1、管道均以直线段铺设,不考虑地形影响。
2、不考虑管道的接头处费用。
3、不考虑施工之中的意外情况,所有工作均可顺利进行。
4、共用管线的价格如果和非公用管线不一致,则共用管线价格大于任意一条非公用管线价格,小于两条非公用管线价格之和。
问题分析:
问题一:要考虑有和没有共用管线,还要考虑共用管线与非共用管线费用相同和不同两种情况。同时还要考虑两个工厂是否在铁路的同一侧,如果两个工厂在铁路的同一侧那么一定没有共用管线。 不在铁路的同一侧那么就要考虑有和没有共用管线这个问题。计算共用管线的长度时,用光学原理,把一个工厂当作光源发射一束光经过一个平面的反射通过另一个工厂,这样能够保证路线最短。这个平面与铁路的距离即为共用管线的长度。同时与这个平面的交点就是两厂的管线的交点。当共用管线与非共用管线费用不相同时可以通过建立方程组来解答。
当共用管线与非共用管线费用不相同时要建立方程组来计算其最小费用从而来确定方案的可行性,共用管线与非共用管线长度作为变量来控制总费用,那么我们就可以列出一个方程组,从而在变量的约束条件下可以确定最小费用。
问题二:把这个问题分两部分来考虑,即市区和郊区分两个部分,火车站建立在郊区费用要小得多,郊区共用管线与非共用管线的费用相同所以可以用最短路径的方法来考虑,同时又要求费用最小,可以解出最低费用及对应的铺设线路。
问题三:通过建立坐标系设两个点的坐标,同时也是表达管线的长度,然后再与各自的费用之积确定总的费用,从而算出两点的坐标值。即确定了管线的路线。
模型的建立与求解整体论文缩略图

全部论文请见下方“ 只会建模 QQ名片” 点击QQ名片即可
部分程序代码:
%解方程组
syms x y b l a m n
[x,y]=solve('x/((x^2+(y-a)^2)^(1/2))+(x-l)/(((x-l)^2+(y-b)^2)^(1/2))=0','m*((y-a)/((x^2+(y-a)^2)^(1/2))+(y-b)/(((x-l)^2+(y-b)^2)^(1/2)))+n=0','x,y');
pretty(simple(x))
pretty(simple(y))
%铺设管路长度
syms m n a b l
x =-1/4/(-4*m^2+n^2)*(-8*a*m^2+8*b*m^2-2*n^2*b+2*n^2*a+2*(4*m^2*l^2*n^2-l^2*n^4)^(1/2))*l/(-1/2/(-4*m^2+n^2)*(-8*a*m^2+8*b*m^2-2*n^2*b+2*n^2*a+2*(4*m^2*l^2*n^2-l^2*n^4)^(1/2))+a-b)y =a-1/4/(-4*m^2+n^2)*(-8*a*m^2+8*b*m^2-2*n^2*b+2*n^2*a+2*(4*m^2*l^2*n^2-l^2*n^4)^(1/2))
d=(x^2+(a-y)^2)^(1/2)+((l-x)^2+(b-y)^2)^(1/2)+y
pretty(simple(d))
syms m n a b l
x=-1/4/(n^2-4*m^2)*(-8*m^2*a+8*m^2*b+2*n^2*a-2*n^2*b-2*(4*m^2*l^2*n^2-l^2*n^4)^(1/2))*l/(-1/2/(n^2-4*m^2)*(-8*m^2*a+8*m^2*b+2*n^2*a-2*n^2*b-2*(4*m^2*l^2*n^2-l^2*n^4)^(1/2))+a-b)y=a-1/4/(n^2-4*m^2)*(-8*m^2*a+8*m^2*b+2*n^2*a-2*n^2*b-2*(4*m^2*l^2*n^2-l^2*n^4)^(1/2))f=(x^2+(a-y)^2)^(1/2)+((l-x)^2+(b-y)^2)^(1/2)+ypretty(simple(f))
%铺设管路所需费用
syms m n a b l
x =-1/4/(-4*m^2+n^2)*(-8*a*m^2+8*b*m^2-2*n^2*b+2*n^2*a+2*(4*m^2*l^2*n^2-l^2*n^4)^(1/2))*l/(-1/2/(-4*m^2+n^2)*(-8*a*m^2+8*b*m^2-2*n^2*b+2*n^2*a+2*(4*m^2*l^2*n^2-l^2*n^4)^(1/2))+a-b)y =a-1/4/(-4*m^2+n^2)*(-8*a*m^2+8*b*m^2-2*n^2*b+2*n^2*a+2*(4*m^2*l^2*n^2-l^2*n^4)^(1/2))
e=m*(x^2+(a-y)^2)^(1/2)+m*((l-x)^2+(b-y)^2)^(1/2)+n*y
pretty(simple(e))
syms m a b lx=-1/4/(m^2-4*m^2)*(-8*m^2*a+8*m^2*b+2*m^2*a-2*m^2*b-2*(4*m^2*l^2*m^2-l^2*m^4)^(1/2))*l/(-1/2/(m^2-4*m^2)*(-8*m^2*a+8*m^2*b+2*m^2*a-2*m^2*b-2*(4*m^2*l^2*m^2-l^2*m^4)^(1/2))+a-b)y=a-1/4/(m^2-4*m^2)*(-8*m^2*a+8*m^2*b+2*m^2*a-2*m^2*b-2*(4*m^2*l^2*m^2-l^2*m^4)^(1/2))g=m*(x^2+(a-y)^2)^(1/2)+m*((l-x)^2+(b-y)^2)^(1/2)+n*ypretty(simple(g))
!目标函数Z最小;
min=7.2*(a+b+c+d)+21.424*d;
x1<15;
a^2=((x1)^2+(y1-5)^2);!a表示AP;
b^2=((x1-15)^2+(y1-y2)^2); !b表示PQ;
c=y1; !c表示CP;
d^2=((15-20)^2+(y2-8)^2); !d表示QB;LINGO9.0运行结果:
Local optimal solution found.Objective value: 282.3143Total solver iterations: 46Variable Value Reduced CostA 6.294130 -0.4507570E-08B 11.02638 0.000000C 1.852935 0.000000D 5.040020 0.2173971E-07X1 5.450877 0.000000Y1 1.852935 0.2237103E-07Y2 7.366124 0.000000Row Slack or Surplus Dual Price1 282.3143 -1.0000002 9.549123 0.0000003 0.000000 -0.57196154 0.000000 -0.32648985 0.000000 -7.2000006 0.000000 -2.839671
全部论文请见下方“ 只会建模 QQ名片” 点击QQ名片即可
相关文章:

2010年国赛高教杯数学建模C题输油管的布置解题全过程文档及程序
2010年国赛高教杯数学建模 C题 输油管的布置 某油田计划在铁路线一侧建造两家炼油厂,同时在铁路线上增建一个车站,用来运送成品油。由于这种模式具有一定的普遍性,油田设计院希望建立管线建设费用最省的一般数学模型与方法。 1. 针对两炼…...
datawhale大模型bot应用开发--task3:工作流
目录 一、介绍:Coze工作流 1.1工作流应用场景 1.2什么是工作流 1.3思考环节 二、各个工作流详情 2.1情感分类工作流 2.2 随机数工作流 2.3 必应搜索工作流 2.4 天气查询工作流 三、集合上面五个工作流的总工作流 一、介绍:Coze工作流 1.1工作…...

期货配资系统风控逻辑开发/完整源代码
期货配资系统风控逻辑的开发是确保系统安全、稳定、高效运行的关键环节。以下是对期货配资系统风控逻辑开发的详细分析: 一、风险识别与评估 风险来源分析: 市场风险:期货市场价格波动带来的风险。信用风险:投资者或配资方违约的…...

汽车免拆诊断案例 | 2023款零跑C01纯电车后备厢盖无法电动打开和关闭
故障现象 一辆2023款零跑C01纯电车,累计行驶里程约为2万km,车主进厂反映,后备厢盖无法电动打开和关闭。 故障诊断 接车后试车,操作后备厢盖外侧、驾驶人侧及遥控钥匙上的后备厢盖开启按钮,可以听到后备厢盖解锁的…...

分布式存储架构 与分布式一致性协议
分布式存储架构可以分为无中心节点架构和有中心节点架构。它们的设计在系统中的角色分配、数据管理、协调方式等方面有所不同。 1. 无中心节点架构(Decentralized/Peer-to-Peer Architecture) 在无中心节点的分布式存储架构中,所有节点都是…...
Unity Apple Vision Pro 保姆级开发教程 - Simulator 模拟器使用
教程视频 Apple VisionPro Simulator 模拟器使用教程 VsionOS Simulator 简介 visionOS Simulator 是一个用于开发和测试 visionOS 应用程序的工具。它模拟 Apple Vision Pro 的运行环境,帮助开发者在没有硬件设备的情况下创建、调试和优化他们的应用程序。VisionO…...

Vue 之 插件与组件的区别
在 Vue.js 中,插件(Plugin)和组件(Component)都是用来扩展 Vue 功能的重要工具,但它们的应用场景和使用方式有所不同。本文将通过对比的方式,帮助开发者更好地理解两者的区别,并通过…...

了解 ChatGPT 中的公平性问题
了解 ChatGPT 中的公平性问题 最近,OpenAI 又发布了一篇新的博客。他们谈论了一个有趣又重要的话题——用户的身份如何影响 ChatGPT 的回答。 这项研究揭示了一个鲜明的事实,那就是 AI 可能会无意间对人类产生刻板印象。很可能这些刻板印象源自 AI 训练过程中使用的数据,而这…...

【PHP】安装swoole时报错:No package ‘libbrotlienc‘ found
一、环境 Debian 11(bullseye) PHP 8.2.14 Swoole 5.1.4 二、过程 今天在安装Swoole 5.1.4的时候报错,错误信息如下: configure: error: Package requirements (libbrotlienc) were not met:No package libbrotlienc foundConsider adjusting the PK…...
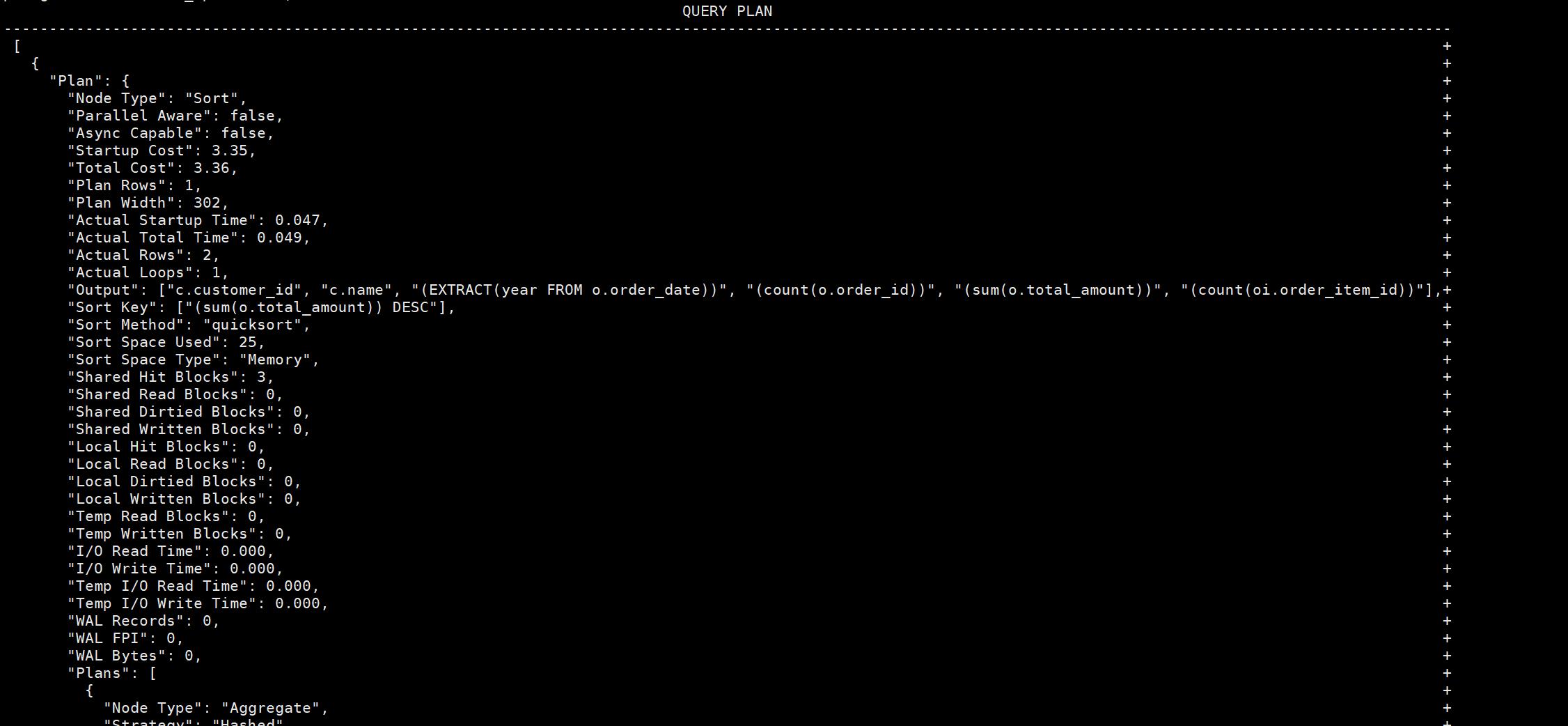
postgresql执行计划解读案例
简介 SQL优化中读懂执行计划尤其重要,以下举例说明在执行计划中常见的参数其所代表的含义。 创建测试数据 -- 创建测试表 drop table if exists customers ; drop table if exists orders ; drop table if exists order_items ; drop table if exists products ;…...
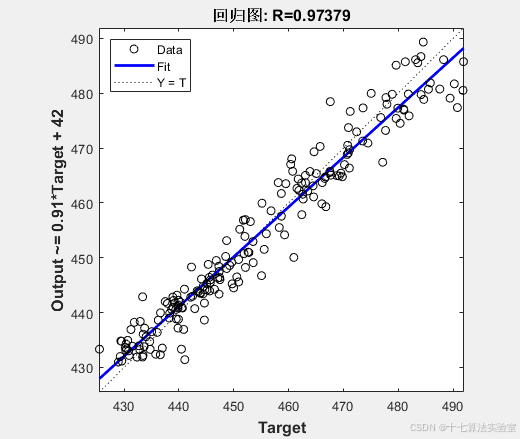
Matlab实现粒子群优化算法优化随机森林算法模型 (PSO-RF)(附源码)
目录 1.内容介绍 2.部分代码 3.实验结果 4.内容获取 1内容介绍 粒子群优化算法(PSO)是一种启发式搜索方法,灵感来源于鸟类群体觅食的行为。在PSO中,每个解都是搜索空间中的一个“粒子”,这些粒子以一定的速度飞行&am…...

使用 EasyExcel 相邻数据相同时行和列的合并,包括动态表头、数据
前言 在处理 Excel 文件时,经常会遇到需要对表格中的某些单元格进行合并的情况,例如合并相同的行或列。Apache POI 是一个强大的工具,但它使用起来相对复杂。相比之下,EasyExcel 是一个基于 Apache POI 的轻量级 Excel 处理库&am…...

985研一学习日记 - 2024.10.16
一个人内耗,说明他活在过去;一个人焦虑,说明他活在未来。只有当一个人平静时,他才活在现在。 日常 1、起床6:00√ 2、健身1个多小时 今天练了二头和背部,明天练胸和三头 3、LeetCode刷了3题 旋转图像:…...

安装mysql 5.5.62
1>先检查是否存在其他版本mysql rpm -qa|grep -i mariadb 存在则卸载 yum -y remove maria* 2>下载mysql 5.5.62 wget https://cdn.mysql.com/archives/mysql-5.5/mysql-5.5.62-linux-glibc2.12-x86_64.tar.gz 3>确认系统是否安装libaio库 yum -y install libai…...
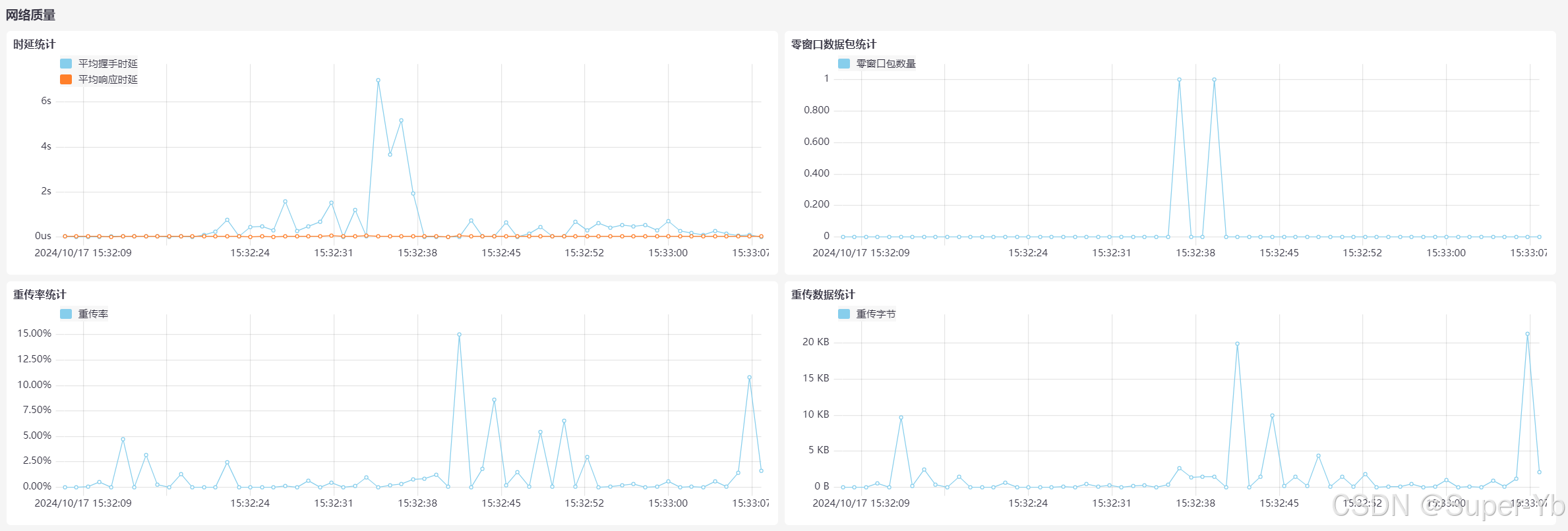
AnaTraf | 网络性能监控系统的价值
目录 1. IT运维工程师 2. 网络管理员 3. 安全团队(网络安全工程师) 4. 业务部门(应用开发人员、产品经理) 5. 管理层与决策者(CTO/CIO、IT经理) 6. 最终用户(普通员工) 总结&…...

决策树和集成学习的概念以及部分推导
一、决策树 1、概述 决策树是一种树形结构,树中每个内部节点表示一个特征上的判断,每个分支代表一个判断结果的输出,每个叶子节点代表一种分类结果 决策树的建立过程: 特征选择:选择有较强分类能力的特征决策树生成…...
servlet基础与环境搭建(idea版)
文章目录 环境变量配置安包装环境变量配置JDK 配置 静态网页动态网页(idea)给模块添加 web框架新版本 2023 之后的 idea,使用方法二idea 目录介绍建立前端代码启动配置 环境变量配置 tomcat 环境变量 安包装 环境变量配置 JDK 配置 静态网页…...

【10月最新】植物大战僵尸杂交版新僵尸预告(附最新版本下载链接)
【BOSS僵尸】埃德加二世 【新BOSS僵尸】埃德加二世 “埃德加博士的克隆体。驾驶着最新一代小型化机甲,致力于为戴夫博士扫清障碍。” -体型(模型大小)小于原版僵王的头 -血量120000(原版僵王复仇的2倍),免疫…...

网络编程-UDP以及数据库mysql
UDP通信流程 服务端客户端有一个邮箱socket()有一个邮箱socket()绑定地址bind()发送数据sendto接收数据recvfrom关闭close()关闭colse() //服务端 #include "head.h" // ./server 10001 int main(int argc,char *argv[]) {// 1、创建socket套接字// 参数1ÿ…...

ubuntu 20.04 安装ros1
步骤 1:设置系统 首先,确保系统环境是最新的: sudo apt update sudo apt upgrade 步骤 2:设置源和密钥 添加 ROS 软件源: 首先,确保 curl 和 gnupg 已安装: sudo apt install curl gnupg2…...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...

算法岗面试经验分享-大模型篇
文章目录 A 基础语言模型A.1 TransformerA.2 Bert B 大语言模型结构B.1 GPTB.2 LLamaB.3 ChatGLMB.4 Qwen C 大语言模型微调C.1 Fine-tuningC.2 Adapter-tuningC.3 Prefix-tuningC.4 P-tuningC.5 LoRA A 基础语言模型 A.1 Transformer (1)资源 论文&a…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...
