Leetcode 剑指 Offer II 098.不同路径
题目难度: 中等
原题链接
今天继续更新 Leetcode 的剑指 Offer(专项突击版)系列, 大家在公众号 算法精选 里回复
剑指offer2就能看到该系列当前连载的所有文章了, 记得关注哦~
题目描述
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。
问总共有多少条不同的路径?
示例 1:

- 输入:m = 3, n = 7
- 输出:28
示例 2:
- 输入:m = 3, n = 2
- 输出:3
- 解释:从左上角开始,总共有 3 条路径可以到达右下角。
- 向右 -> 向下 -> 向下
- 向下 -> 向下 -> 向右
- 向下 -> 向右 -> 向下
示例 3:
- 输入:m = 7, n = 3
- 输出:28
示例 4:
- 输入:m = 3, n = 3
- 输出:6
提示:
- 1 <= m, n <= 100
- 题目数据保证答案小于等于 2 * 10^9
题目思考
- 如何优化时间和空间复杂度?
解决方案
方法 1
- 分析题目, 机器人只能向下或向右移动, 我们可以利用这一点, 累加当前坐标的左边和上边相邻坐标的路径数来得到当前坐标的路径数
- 显然这就是动态规划的思路:
- 设
dp[r][c]代表坐标(r,c)的路径数 - 初始化
dp[0][0] = 1, 其他值全是 0, 表示开始时起点的路径数为 1 - 然后进行状态转移:
dp[r][c] = dp[r-1][c] + dp[r][c-1](如果 r 或 c 为 0, 则相应的 r-1 或 c-1 的 dp 值就是 0, 只能从另一个方向转移而来) - 最终右下角坐标的
dp[m-1][n-1]就代表总路径数
- 设
- 下面的代码有详细的注释, 方便大家理解
复杂度
- 时间复杂度
O(MN): 需要两重循环求 DP 值 - 空间复杂度
O(MN): 二维 DP 数组的空间消耗
代码
class Solution:def uniquePaths(self, m: int, n: int) -> int:dp = [[0] * n for _ in range(m)]for r in range(m):for c in range(n):if (r, c) == (0, 0):# 起点dp值初始化为1dp[r][c] = 1else:# 左侧邻居路径数, 不存在时为0ldp = 0 if c == 0 else dp[r][c - 1]# 上侧邻居路径数, 不存在时为0udp = 0 if r == 0 else dp[r - 1][c]# 累加两个邻居的路径数dp[r][c] = ldp + udp# 最终结果就是右下角路径数return dp[m - 1][n - 1]
方法 2
- 上面的 DP 做法固然可以解决这个问题, 那是否可以继续优化呢?
- 答案是肯定的, 我们从另一个角度来思考这个问题, 机器人一共移动 m+n-2 次, 然后每次移动要么向下, 要么向右, 一共向下移动 m-1 次, 向右移动 n-1 次
- 相当于从总移动次数 m+n-2 中选取 m-1 个, 我们可以利用数学求组合数的方法, 也即
C(m+n-2, m-1), 得到的值就是对应的总路径数 - 这里可以额外进行一些优化, 使用 m 和 n 中的较小值来计算组合数, 对应的时间复杂度也是两者的较小值
- 下面的代码有详细的注释, 方便大家理解
复杂度
- 时间复杂度
O(min(M,N)): 求组合数时需要累乘 M-1 或 N-1 次, 取两者较小值 - 空间复杂度
O(1): 没有使用额外变量
代码
class Solution:def uniquePaths(self, m: int, n: int) -> int:# 共有m+n-2次移动, 然后从中选择m-1次向下, 剩下n-1次向右# 所以总路径数就是组合数C(m+n-2,m-1) (也等于C(m+n-2,n-1))# 额外优化, 使用m和n的较小值来计算组合数mn = min(m, n)return math.comb(m + n - 2, mn - 1)
大家可以在下面这些地方找到我~😊
我的 GitHub
我的 Leetcode
我的 CSDN
我的知乎专栏
我的头条号
我的牛客网博客
我的公众号: 算法精选, 欢迎大家扫码关注~😊

相关文章:

Leetcode 剑指 Offer II 098.不同路径
题目难度: 中等 原题链接 今天继续更新 Leetcode 的剑指 Offer(专项突击版)系列, 大家在公众号 算法精选 里回复 剑指offer2 就能看到该系列当前连载的所有文章了, 记得关注哦~ 题目描述 一个机器人位于一个 m x n 网格的左上角 (起始点在下…...
LabVIEW智能螺杆空压机测试系统
基于LabVIEW软件开发的螺杆空压机测试系统利用虚拟仪器技术进行空压机的性能测试和监控。系统能够实现对螺杆空压机关键性能参数如压力、温度、流量、转速及功率的实时采集与分析,有效提高测试效率与准确性,同时减少人工操作,提升安全性。 项…...

在 Ubuntu 22.04 上安装 PHP 8.2
在 Ubuntu 22.04 上安装 PHP 8.2,可以按照以下步骤进行: 更新系统软件包: 首先,确保你的系统软件包是最新的。 sudo apt update sudo apt upgrade 安装 PHP PPA(Personal Package Archive): U…...

Java生死簿管理小系统(简单实现)
学习总结 1、掌握 JAVA入门到进阶知识(持续写作中……) 2、学会Oracle数据库入门到入土用法(创作中……) 3、手把手教你开发炫酷的vbs脚本制作(完善中……) 4、牛逼哄哄的 IDEA编程利器技巧(编写中……) 5、面经吐血整理的 面试技…...

【VoceChat】一个即时聊天(IM)软件,又是一个可以嵌入任何网页聊天系统
为什么要搭建私人聊天软件 在当今数字化时代,聊天软件已经成为人们日常沟通和协作的重要工具。市面上的公共聊天平台虽然方便,但也伴随着诸多隐私、安全、广告和功能限制的问题。对于那些注重数据安全、追求高效沟通的个人或团队来说,搭建一…...

【LeetCode】动态规划—96. 不同的二叉搜索树(附完整Python/C++代码)
动态规划—96. 不同的二叉搜索树 题目描述前言基本思路1. 问题定义2. 理解问题和递推关系二叉搜索树的性质:核心思路:状态定义:状态转移方程:边界条件: 3. 解决方法动态规划方法:伪代码: 4. 进一…...
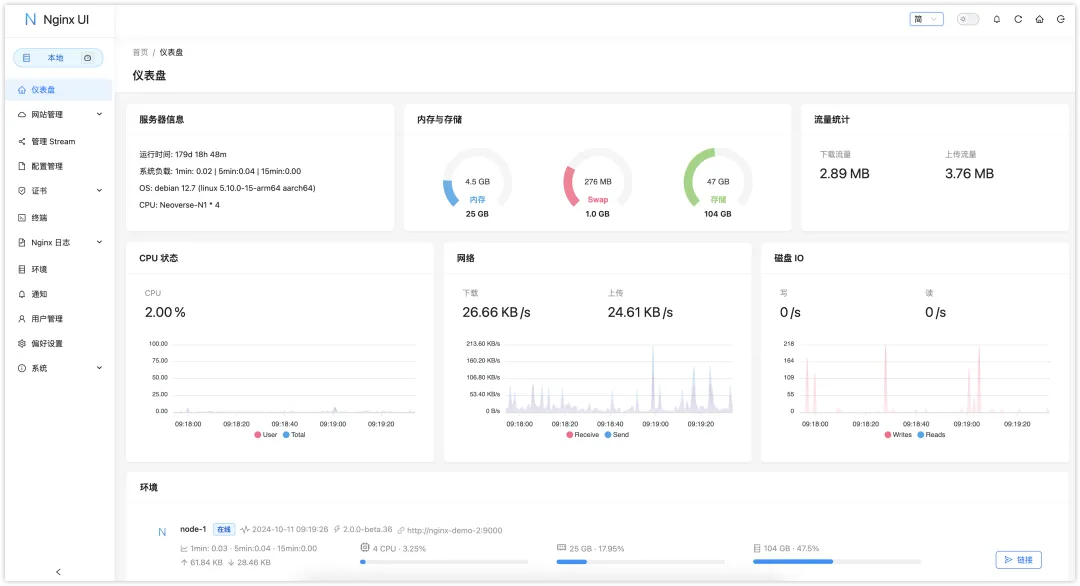
Nginx UI 一个可以管理Nginx的图形化界面工具
Nginx UI 是一个基于 Web 的图形界面管理工具,支持对 Nginx 的各项配置和状态进行直观的操作和监控。 Nginx UI 的功能非常丰富: 在线查看服务器 CPU、内存、系统负载、磁盘使用率等指标 在线 ChatGPT 助理 一键申请和自动续签 Let’s encrypt 证书 在…...

Vue向上滚动加载数据时防止内容闪动
目前的需求:当前组件向上滚动加载数据,dom加载完后,页面的元素位置不能发生变化 遇到的问题:加载完数据后,又把滚轮滚到之前记录的位置时,内容发生闪动 现在的方案: 加载数据之前记录整体滚动条…...

基于QT、ARM的智能停车管理系统+高分项目+源码
Parking-management-system 本系统基于QT、ARM开发板、Linux系统并对接百度AI 1.1 项目目的: 创建一个智能停车管理系统,能够停入车辆和取出车辆以及查询车辆停入停车场的状态并且计算车辆离开时收费情况。 1.2 项目意义: 实现停车场智能抬杆和智能收费系统&…...

1.6,unity动画Animator屏蔽某个部位,动画组合
动画组合 一边跑一边攻击 using System.Collections; using System.Collections.Generic; using UnityEngine;public class One : MonoBehaviour {private Animator anim;// Start is called before the first frame updatevoid Start(){anim GetComponent<Animator>();…...

发动机冷却系统排空气
发动机冷却系统排空气的几种常见方法 发动机冷却系统是汽车发动机的重要组成部分,它的主要作用是通过循环冷却液来吸收和散发发动机产生的热量,确保发动机在正常工作温度下运行。然而,在冷却系统的运行过程中,由于各种原因&#…...

三周精通FastAPI:1 第一步入门
FastAPI是一个非常棒的python web和api框架,准备用三周的时间“精通它” 学习流程参考FastAPI官网的用户教程:教程 - 用户指南 - FastAPI 学前提示 运行代码 所有代码片段都可以复制后直接使用(它们实际上是经过测试的 Python 文件&#x…...

RestTemplate基本使用之HTTP实现GET请求和POST请求
一、GET请求实例 public static TianQi getTianQi(String city) {RestTemplate restTemplate new RestTemplate();HashMap res restTemplate.getForObject("http://www.tianqiapi.com/api/?versionv6&appid15118158&appsecretgVNnwva8&city" city, H…...

2024-10-18 问AI: [AI面试题] 神经网络有哪些不同类型?
文心一言 神经网络有多种不同类型,每种类型都有其特定的结构和应用场景。以下是一些主要的神经网络类型: 前馈神经网络(FNN): 也称为全连接神经网络或感知器网络。由输入层、隐藏层和输出层组成,信息流是单…...

【开源免费】基于SpringBoot+Vue.JS课程作业管理系统(JAVA毕业设计)
本文项目编号 T 023 ,文末自助获取源码 \color{red}{T023,文末自助获取源码} T023,文末自助获取源码 目录 一、系统介绍二、演示录屏三、启动教程四、功能截图五、文案资料5.1 选题背景5.2 国内外研究现状5.3 可行性分析 六、核心代码6.1 查…...

jmeter中对于有中文内容的csv文件怎么保存
jmeter的功能很强大,但是细节处没把握好就得不到预期的结果。今天来讲讲有中文内容的csv文件的参数化使用中需要注意的事项。 对于有中文内容,涉及到编码格式,为了让jmeter能正确地读取csv文件中的中文,需要把文件转码为UTF-8BOM…...

Leetcode 921 Shortest Path in Binary Matrix
题意:求二维矩阵中往8个方向移动的话,从左上方到右下方移动的最短路径 https://leetcode.com/problems/shortest-path-in-binary-matrix/description/ 解答:bfs易得 class Solution { public:int shortestPathBinaryMatrix(vector<vecto…...

第二十二篇——菲欧几何:相对论的数学基础是什么?
目录 一、背景介绍二、思路&方案三、过程1.思维导图2.文章中经典的句子理解3.学习之后对于投资市场的理解4.通过这篇文章结合我知道的东西我能想到什么? 四、总结五、升华 一、背景介绍 对于几何的几个工具,让我再次感叹数学的伟大,逻辑…...

【AI整合包及教程】EchoMimic:开创数字人新时代,让静态图像“活”起来!
在数字化浪潮的推动下,人工智能技术正以前所未有的速度渗透到我们生活的方方面面。从智能家居到自动驾驶,从智能客服到医疗诊断,AI的触角无处不在。而如今,阿里巴巴旗下的蚂蚁集团再次引领潮流,宣布开源其革命性的数字…...

ArcGIS 最新底图服务地址
ArcGIS 最新底图服务地址 说明 先上地址: 地形图: https://services.arcgisonline.com/arcgis/rest/services/Elevation/World_Hillshade/MapServer深色地形图:https://services.arcgisonline.com/arcgis/rest/services/Elevation/World_Hi…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

TRS收益互换:跨境资本流动的金融创新工具与系统化解决方案
一、TRS收益互换的本质与业务逻辑 (一)概念解析 TRS(Total Return Swap)收益互换是一种金融衍生工具,指交易双方约定在未来一定期限内,基于特定资产或指数的表现进行现金流交换的协议。其核心特征包括&am…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...

【生成模型】视频生成论文调研
工作清单 上游应用方向:控制、速度、时长、高动态、多主体驱动 类型工作基础模型WAN / WAN-VACE / HunyuanVideo控制条件轨迹控制ATI~镜头控制ReCamMaster~多主体驱动Phantom~音频驱动Let Them Talk: Audio-Driven Multi-Person Conversational Video Generation速…...

Mysql8 忘记密码重置,以及问题解决
1.使用免密登录 找到配置MySQL文件,我的文件路径是/etc/mysql/my.cnf,有的人的是/etc/mysql/mysql.cnf 在里最后加入 skip-grant-tables重启MySQL服务 service mysql restartShutting down MySQL… SUCCESS! Starting MySQL… SUCCESS! 重启成功 2.登…...
