红黑树的理解与实现(详解)
相关的数据结构:
搜索二叉树-CSDN博客
AVL树的创建与检测-CSDN博客
个人主页:敲上瘾-CSDN博客
个人专栏:游戏、数据结构、c语言基础、c++学习、算法
目录
一、红黑树规则:
二、红黑树的插入
1.变色
2.单旋+变色
3.双旋+变色
三、红黑树的验证
四、源码:
一、红黑树规则:
红黑树规则(重点!):
- 每个结点不是红⾊就是⿊⾊。
- 根结点是⿊⾊的。
- 如果⼀个结点是红⾊的,则它的两个孩⼦结点必须是⿊⾊的,也就是说任意⼀条路径不会有连续的红⾊结点。
- 对于任意⼀个结点,从该结点到其所有NULL结点的简单路径上,均包含相同数量的⿊⾊结点。
红黑树的性质都由以上4点规则决定的,其中的一个性质:红黑树最长路径的节点数量一定不会大于最短路径的两倍。这使得红黑树虽然不是完全平衡但高度差没有那么大,查找效率依旧是longN级别的。
红黑树为什么能实现最长路径不会超过最短路径的两倍呢?我们可以想一想如果其中任意一条路径有n个黑节点,最短路径的颜色是如何分布,最长路径颜色又是如何分布的呢?其实很简单根据第4条规则我们可以最短的路径的节点不可能低于n个,(即最少的时候为n个黑节点)。又由第3条规则可以知道最长的路径的节点数不可能超过2n个,(即最多的时候为n个黑节点,n个红节点)。
所以我们要实现一个红黑树只需要维护以上4条规则即可。
二、红黑树的插入
因为红黑树也是一棵二叉搜索树,所以我们先按二叉搜索树的逻辑将节点进行插入,需要注意插入的是红色节点,因为黑色节点维护起来非常的困难。
(1)如果该新节点的父亲为黑节点,不用再做调整,直接返回。
(2)如果不是则需要分情况进行更新:
在这里我们是因为父亲为红节点才进行更新的,因为在插入之前已经保证这是一棵红黑树,又因为父亲为红色,所以爷爷一定为黑色。
而我们要做的就是把新节点的父亲更新成黑色,如何更新如何分情况呢关键就在于叔叔是否存在以及叔叔的颜色。接下来就以父亲为爷爷的左孩子为例进行讲解,父亲为爷爷的右孩子同理。
说明:下图中假设我们把新增结点标识为c(cur),c的⽗亲标识为p(parent),p的⽗亲标识为
g(grandfather),p的兄弟标识为u(uncle)。
1.变色

叔叔u存在且为红:
该情况比较简单,因为要保持每条路径的黑节点的个数相同,所以直接将g的黑色分配给p和u,而g变为红色即可。如上图:
但是有个问题g的父亲是完全有可能是红节点的,照这样的话又出现了两个连续的红色节点,所以再以g作为新的c节点,g的父亲作为新的p节点,然后更新g,最后循环进行调整就可以解决。
如下x是通过变色更新上来的节点:

2.单旋+变色

叔叔u不存在或为黑:
当叔叔u不存在或为黑,我们发现无论如何变色都是无法调整得当的,所以这就需要旋转+变色操作了。
该情况又可以细分为两种情况:
- c和p在g的同一侧,需要单旋+变色
- c和p在g的不同侧,需要双旋+变色
首先来分析第一种情况:
如下:以g为旋转点进行右旋,然后将p更新为黑色,c和g为红色。

关于旋转请参考:AVL树的创建与检测-CSDN博客
3.双旋+变色
叔叔u不存在或为黑并且c和p在g的不同侧我们进行双旋+变色,如下:


注意:因为考虑要使根节点为黑色,防止在调整过程将根节点改为黑色,所以在每次调整过后直接将根节点更新为黑色。
三、红黑树的验证
红黑树的验证并不用去验证高度差,也不用去验证最长路径的节点数是不是小于最短路径的两倍,因为即使这一些条件都满足也不一定是红黑树,想要验证红黑树只需要验证是否满足红黑树的规则即可,只要满足了那些规则,那么红黑树的性质自然就有了。
- 规则1就不用验证因为这是必然的
- 规则2也是比较简单一个if语句就解决。
- 规则3的验证:遍历整棵树,当遍历到红色节点时判断它的父亲是否为黑色,不是则违反规则。
- 规则4的验证:任意选择一条路径(如一直往左走)并记录其中的黑节点数目(记为count),然后遍历整棵树的所有路径并记录黑节点数目,然后在路径结束后与count比较,如果不相等则违反规则。
四、源码:
#pragma once
#include<iostream>
using namespace std;
enum Color{red, black};
template<class T>
struct RBNode
{RBNode(T key):data(key),color(red),left(nullptr),right(nullptr),prev(nullptr){}T data;enum Color color;RBNode<T>* left;RBNode<T>* right;RBNode<T>* prev;
};
template<class T>
class RBTree
{
public:typedef RBNode<T> Node;RBTree():root(nullptr){}bool insert(T data){Node* newNode = new Node(data);if (root == nullptr){root = newNode;root->color = black;return true;}Node* cur = root;Node* parent = root;while (cur){parent = cur;if (newNode->data.first <= cur->data.first)cur = cur->left;else cur = cur->right;}if (newNode->data.first <= parent->data.first)parent->left = newNode;else parent->right = newNode;newNode->prev = parent;//需要调整cur = newNode;Node* grandfather = parent->prev;Node* uncle = nullptr;while (parent&&parent->color == red){grandfather = parent->prev;if (parent == grandfather->left){uncle = grandfather->right;if (uncle && uncle->color == red){grandfather->color = red;parent->color = uncle->color = black;cur = grandfather;parent = cur->prev;}else{if (cur == parent->left){ReverseR(grandfather);parent->color = black;grandfather->color = red;}else{ReverseL(parent);ReverseR(grandfather);cur->color = black;parent->color = grandfather->color = red;}}}else{uncle = grandfather->left;if (uncle && uncle->color == red){grandfather->color = red;parent->color = uncle->color = black;cur = grandfather;parent = cur->prev;}else{if (cur == parent->right){ReverseL(grandfather);parent->color = black;grandfather->color = red;}else{ReverseR(parent);ReverseL(grandfather);cur->color = black;parent->color = grandfather->color = red;}}}}root->color = black;return true;}void ReverseR(Node* parent){Node* subL = parent->left;Node* subLR = subL->right;parent->left=subLR;subL->right = parent;//Node* pparent = parent->prev;subL->prev = pparent;if (pparent == nullptr) root = subL;else{if (pparent->left == parent) pparent->left = subL;else pparent->right = subL;}if (subLR) subLR->prev = parent;parent->prev = subL;}void ReverseL(Node* parent){Node* subR = parent->right;Node* subRL = subR->left;parent->right = subRL;subR->left = parent;//Node* pparent = parent->prev;subR->prev = pparent;if (pparent == nullptr) root = subR;else{if (pparent->left == parent) pparent->left = subR;else pparent->right = subR;}if (subRL) subRL->prev = parent;parent->prev = subR;}bool IsBalanceTree(){if (root == nullptr) return true;if (root->color == red) return false;int count = 0;Node* cur = root;while (cur){if (cur->color == black) count++;cur = cur->left;}return Check(root, 0, count);}bool Check(Node* root,int path,const int refNum){if (root == nullptr) return path == refNum;if (root->color == red && root->prev->color == red) return false;if (root->color == black) path++;return Check(root->left, path, refNum) && Check(root->right, path, refNum);}
private:Node* root;
};相关文章:

红黑树的理解与实现(详解)
相关的数据结构: 搜索二叉树-CSDN博客 AVL树的创建与检测-CSDN博客 个人主页:敲上瘾-CSDN博客 个人专栏:游戏、数据结构、c语言基础、c学习、算法 目录 一、红黑树规则: 二、红黑树的插入 1.变色 2.单旋变色 3.双旋变色 三、…...

从一到无穷大 #37 Databricks Photon:打响 Spark Native Engine 第一枪
本作品采用知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议进行许可。 本作品 (李兆龙 博文, 由 李兆龙 创作),由 李兆龙 确认,转载请注明版权。 文章目录 引言技术决策JVM vs. Native ExecutionInterpreted Vectorization vs Code-GenRow vs…...

Java 字符串占位格式化
Java 提供了几种方式来处理字符串占位符,最常用的是 String 类的 format 方法和 MessageFormat 类。以下是这两种方法的详细说明和示例。 1、String.format 基本语法: String formatted String.format("格式字符串", 参数1, 参数2, ...); …...

基于netty实现简易版rpc服务-理论分析
1.技术要点 1.1 rpc协议 定义一个rpc协议类,用于rpc服务端和客户端数据交互。 1.2 netty粘包半包处理 由于数据传说使用tcp协议,rpc协议的数据在网络传输过程中会产生三种情况: 1)刚好是完整的一条rpc协议数据 2)不…...

Elasticsearch高级搜索技术-全文搜索
目录 倒排索引 (Inverted Index) 示例 分词器 (Analyzer) 评分机制 (Scoring) 查询执行 match 查询 match_phrase 查询 全文搜索是Elasticsearch的核心功能之一,它通过复杂的算法和数据结构来提供高效的搜索能力。为了深入理解其工作原理,我们需要…...
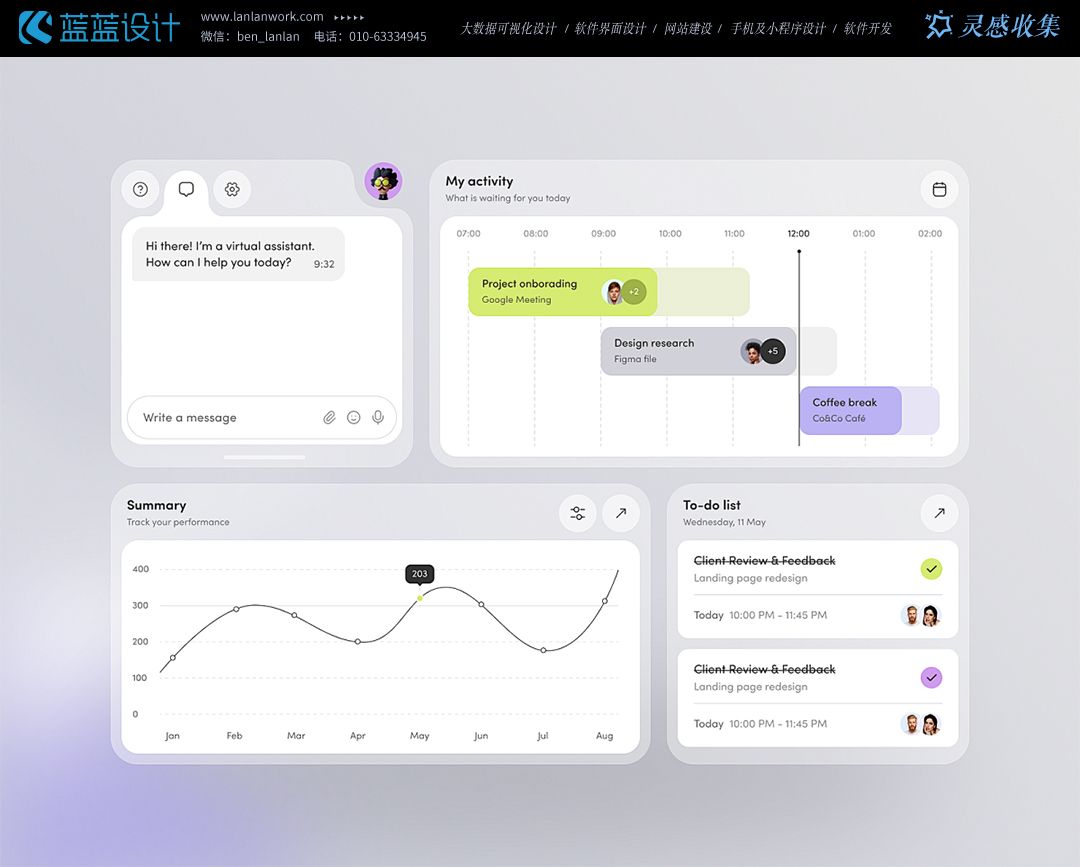
案例分享—国外优秀UI卡片设计作品赏析
国外UI设计注重用户体验,倾向于采用简洁的布局、清晰的排版和直观的交互方式,减少用户的认知负担。卡片式设计能够完美利用屏幕空间,使内容一目了然,易于用户快速浏览和阅读,从而提升了整体的用户体验。 更加注重扁平化…...

Go语言基础学习(Go安装配置、基础语法)
一、简介及安装教程 1、为什么学习Go? 简单好记的关键词和语法;更高的效率;生态强大;语法检查严格,安全性高;严格的依赖管理, go mod 命令;强大的编译检查、严格的编码规范和完整的…...

STM32—FLASH闪存
1.FLASH简介 STM32F1系列的FLASH包含程序存储器、系统存储器和选项字节三个部分,通过闪存存储器接口(外设)可以对程序存储器和选项字节进行擦除和编程 我们怎么操作这些存储器呢?这就需要用到这个闪存存储器接口了,闪…...
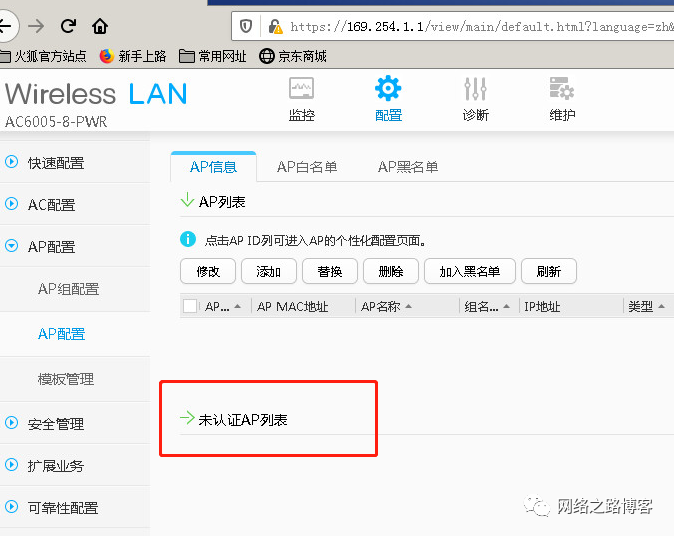
AP上线的那些事儿(1)capwap建立过程、设备初始化以及二层上线
1、了解FITAP与AC的建立过程 之前我们已经知道了FATAP与FIT是一对双胞胎一样的兄弟,FAT哥哥能够直接独立使用当AP桥接、路由器等,而弟弟FIT则比较薄弱,独自发挥不出功效,需要一位师傅(AC)来带领,…...

10 django管理系统 - 管理员管理 - 新建管理员(通过模态框和ajax实现)
在文章“04 django管理系统 - 部门管理 - 新增部门”中,我们通过传统的新增页面来实现部门的添加。 在本文中,我们通过模态框和ajax来实现管理员的新增。 首先在admin_list.html中新建入口,使用按钮 <div class"panel-heading&quo…...
类型及长度的解释)
Mysql中表字段VARCHAR(N)类型及长度的解释
本文将针对MySQL 中 varchar (N)类型字段的存储方式进行解释,主要是对字符和字节的关系的理解。 1. varchar (N) 中的 N varchar (N) 中的 N 表示字符数,而不是字节数。这意味着 N 表示你可以存储多少个字符。 字符数:指的是字符的个数&…...

git提交信息写错处理方式
在Git中,你可以通过使用rebase命令来合并提交记录。以下是一个简单的步骤来合并一系列提交: 使用git rebase -i开始交互式变基。在打开的编辑器中,你会看到一个提交列表。若要合并提交,将要合并的提交前面的pick改为squash或s。保…...

C#从零开始学习(用unity探索C#)(unity Lab1)
初次使用Unity 本章所有的代码都放在 https://github.com/hikinazimi/head-first-Csharp Unity的下载与安装 从 unity官网下载Unity Hub Unity的使用 安装后,注册账号,下载unity版本,然后创建3d项目 设置窗口界面布局 3D对象的创建 点击对象,然后点击Move Guzmo,就可以拖动…...

【SpringBoot】15 Echarts+Thymeleaf 绘制各种图表
Gitee仓库 https://gitee.com/Lin_DH/system 介绍 ECharts是百度开源的一个前端组件。它是一个使用 JavaScript 实现的开源可视化库,可以流畅的运行在 PC 和移动设备上,兼容当前绝大部分浏览器(IE8/9/10/11,Chrome,…...

网络学习笔记
一、网络的结构与功能 网络的鲁棒性与抗毁性 如果在移走少量节点后网络中的绝大部分节点仍然是连通的,那么就该网络的连通性对节点故障具有鲁棒性 网络上的动力学 动力系统:自旋、振子或混沌的同步、可激发系统 传播过程:信息传播与拥堵…...

[论文笔记]HERMES 3 TECHNICAL REPORT
引言 今天带来论文HERMES 3 TECHNICAL REPORT,这篇论文提出了一个强大的工具调用模型,包含了训练方案介绍。同时提出了一个函数调用标准。 为了简单,下文中以翻译的口吻记录,比如替换"作者"为"我们"。 聊天模…...

MySQL-19.多表设计-一对多-外键
一.多表问题分析 二.添加外键 三.外键约束的问题...

MySQL程序介绍<一>
目录 MySQL程序简介 mysqld - MySQL 服务器 编辑 mysql - MySQL 命令⾏客⼾端 MySQL程序简介 1.MySQL安装完成通常会包含如下程序: Linux系统程序⼀般在 /usr/bin⽬录下,可以通过命令查看 windows系统⽬录: 你的安装路径\MySQL Server…...

Leetcode 第 419 场周赛题解
Leetcode 第 419 场周赛题解 Leetcode 第 419 场周赛题解题目1:3318. 计算子数组的 x-sum I思路代码复杂度分析 题目2:3319. 第 K 大的完美二叉子树的大小思路代码复杂度分析 题目3:思路代码复杂度分析 题目4:3321. 计算子数组的 …...

那些年 我们说走就走
那些年 我们说走就走 —— 2022-03-20 二月十八 春分 我总是钟情于原生景色,犹如那句 “落霞与孤鹜齐飞,秋水共长天一色。” 所绘。 我热爱骑行,向往自然,对有着 “中国人的景观大道” 之称的 318 国道川藏线憧憬已久。 17 年暑…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...
-----深度优先搜索(DFS)实现)
c++ 面试题(1)-----深度优先搜索(DFS)实现
操作系统:ubuntu22.04 IDE:Visual Studio Code 编程语言:C11 题目描述 地上有一个 m 行 n 列的方格,从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子,但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...

HDFS分布式存储 zookeeper
hadoop介绍 狭义上hadoop是指apache的一款开源软件 用java语言实现开源框架,允许使用简单的变成模型跨计算机对大型集群进行分布式处理(1.海量的数据存储 2.海量数据的计算)Hadoop核心组件 hdfs(分布式文件存储系统)&a…...

CVE-2020-17519源码分析与漏洞复现(Flink 任意文件读取)
漏洞概览 漏洞名称:Apache Flink REST API 任意文件读取漏洞CVE编号:CVE-2020-17519CVSS评分:7.5影响版本:Apache Flink 1.11.0、1.11.1、1.11.2修复版本:≥ 1.11.3 或 ≥ 1.12.0漏洞类型:路径遍历&#x…...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...
