CLion和Qt 联合开发环境配置教程（Windows和Linux版）
需要安装的工具CLion 和Qt
CLion下载链接 :https://www.jetbrains.com.cn/clion/
这个软件属于直接默认安装就行，很简单，不多做介绍了
Qt:https://mirrors.tuna.tsinghua.edu.cn/qt/official_releases/online_installers/
window 直接点exe
Linux 先chmod +x xxxx.run赋予可执行权限，然后./xxx.run运行安装，另外ubuntu需要执行sudo apt install libglx-dev libgl1-mesa-dev
项目创建
Windows (标红的地方注意一下)
Linux (标红的地方注意一下）
项目运行
正常创建完是可以直接运行的。如下图所示：
Qt Designer 和Qt UIC 配置
注：windows需要配置Qt Designer ， Qt UIC ,Linux 只需要配置 Qt Designer
File-> settings -> External Tools
Qt Designer 配置，标红的地方改成自己的路径
Qt UIC 配置，标红的地方改成自己的路径
相关文章：
CLion和Qt 联合开发环境配置教程（Windows和Linux版）
需要安装的工具CLion 和Qt CLion下载链接 :https://www.jetbrains.com.cn/clion/ 这个软件属于直接默认安装就行，很简单，不多做介绍了 Qt:https://mirrors.tuna.tsinghua.edu.cn/qt/official_releases/online_installers/ window 直接点exe Linux 先c…...
Qt记录使用QtAwesome
Qt记录使用QtAwesome 基本使用 基本使用 pro文件添加 CONFIG fontAwesomeFree include(QtAwesome/QtAwesome.pri) //实例化QtAwesome fa::QtAwesome* awesome new fa::QtAwesome(this); awesome->initFontAwesome();//设置外置适应 图标ICON的颜色color QVariantMap opt…...
ES6新增promise（异步编程新解决方案）如何封装ajax？
1.什么是异步？ 异步是指从程序在运行过程中可以先执行其他操作。 2.什么是promise？ Promise 是 ES6 引入的异步编程的新解决方案。语法上 Promise 是一个构造函数，用来封装异步 操作并可以获取其成功或失败的结果； 3.promise成功…...
Kubernetes--深入理解Service与CoreDNS
文章目录 Service功能Service 的常见使用场景 Service的模式iptablesIPVS Service类型ClusterIPNodePortLoadBalancerExternalName Service的工作机制EndpointEndpoint 与 Service 的关系Endpoint 的工作原理命令操作 CoreDNSCoreDNS 的配置CoreDNS 的典型插件Corefile 示例Cor…...
AI大模型：开启智能革命新纪元
1.AI大模型技术：智能革命的新引擎 自2022年11月30日OpenAI推出ChatGPT以来，这一大型语言模型（LLM）迅速走红，标志着AI领域进入了一个新的发展阶段，即AI大模型时代。 这一时代预示着AI正朝着通用人工智能&am…...
快速上手C语言【下】（非常详细！！！)
目录 1. 指针 1.1 指针是什么 1.2 指针类型 1.2.1 指针-整数 1.2.2 指针解引用 1.3 const修饰 1.4 字符指针 1.5 指针-指针 1.6 二级指针 2. 数组 2.1 定义和初始化 2.2 下标引用操作符[ ] 2.3 二维数组 2.4 终极测试 3. 函数 3.1 声明和定义 3.2 传值调用…...
红黑树的理解与实现（详解）
相关的数据结构： 搜索二叉树-CSDN博客 AVL树的创建与检测-CSDN博客 个人主页：敲上瘾-CSDN博客 个人专栏：游戏、数据结构、c语言基础、c学习、算法 目录 一、红黑树规则： 二、红黑树的插入 1.变色 2.单旋变色 3.双旋变色 三、…...
从一到无穷大 #37 Databricks Photon：打响 Spark Native Engine 第一枪
本作品采用知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议进行许可。 本作品 (李兆龙 博文, 由 李兆龙 创作)，由 李兆龙 确认，转载请注明版权。 文章目录 引言技术决策JVM vs. Native ExecutionInterpreted Vectorization vs Code-GenRow vs…...
Java 字符串占位格式化
Java 提供了几种方式来处理字符串占位符，最常用的是 String 类的 format 方法和 MessageFormat 类。以下是这两种方法的详细说明和示例。 1、String.format 基本语法： String formatted String.format("格式字符串", 参数1, 参数2, ...); …...
基于netty实现简易版rpc服务-理论分析
1.技术要点 1.1 rpc协议 定义一个rpc协议类，用于rpc服务端和客户端数据交互。 1.2 netty粘包半包处理 由于数据传说使用tcp协议，rpc协议的数据在网络传输过程中会产生三种情况： 1）刚好是完整的一条rpc协议数据 2）不…...
Elasticsearch高级搜索技术-全文搜索
目录 倒排索引 (Inverted Index) 示例 分词器 (Analyzer) 评分机制 (Scoring) 查询执行 match 查询 match_phrase 查询 全文搜索是Elasticsearch的核心功能之一，它通过复杂的算法和数据结构来提供高效的搜索能力。为了深入理解其工作原理，我们需要…...
案例分享—国外优秀UI卡片设计作品赏析
国外UI设计注重用户体验，倾向于采用简洁的布局、清晰的排版和直观的交互方式，减少用户的认知负担。卡片式设计能够完美利用屏幕空间，使内容一目了然，易于用户快速浏览和阅读，从而提升了整体的用户体验。 更加注重扁平化…...
Go语言基础学习(Go安装配置、基础语法)
一、简介及安装教程 1、为什么学习Go？ 简单好记的关键词和语法；更高的效率；生态强大；语法检查严格，安全性高；严格的依赖管理， go mod 命令；强大的编译检查、严格的编码规范和完整的…...
STM32—FLASH闪存
1.FLASH简介 STM32F1系列的FLASH包含程序存储器、系统存储器和选项字节三个部分，通过闪存存储器接口（外设）可以对程序存储器和选项字节进行擦除和编程 我们怎么操作这些存储器呢？这就需要用到这个闪存存储器接口了，闪…...
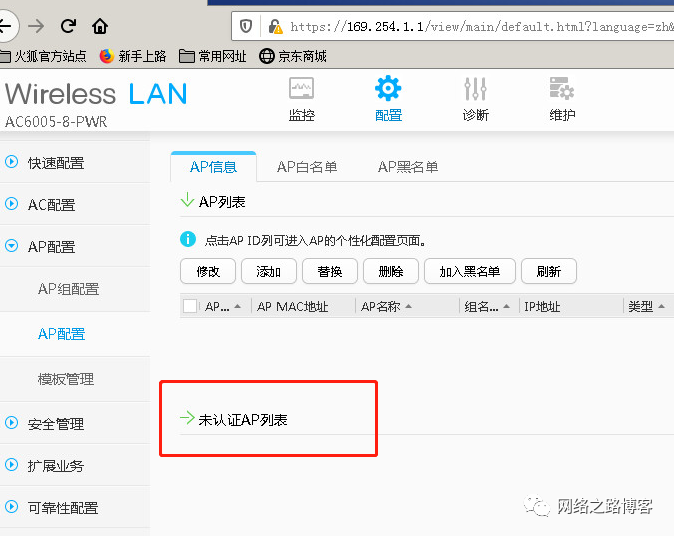
AP上线的那些事儿（1）capwap建立过程、设备初始化以及二层上线
1、了解FITAP与AC的建立过程 之前我们已经知道了FATAP与FIT是一对双胞胎一样的兄弟，FAT哥哥能够直接独立使用当AP桥接、路由器等，而弟弟FIT则比较薄弱，独自发挥不出功效，需要一位师傅（AC）来带领，…...
10 django管理系统 - 管理员管理 - 新建管理员（通过模态框和ajax实现）
在文章“04 django管理系统 - 部门管理 - 新增部门”中，我们通过传统的新增页面来实现部门的添加。 在本文中，我们通过模态框和ajax来实现管理员的新增。 首先在admin_list.html中新建入口，使用按钮 <div class"panel-heading&quo…...
类型及长度的解释)
Mysql中表字段VARCHAR(N)类型及长度的解释
本文将针对MySQL 中 varchar (N)类型字段的存储方式进行解释，主要是对字符和字节的关系的理解。 1. varchar (N) 中的 N varchar (N) 中的 N 表示字符数，而不是字节数。这意味着 N 表示你可以存储多少个字符。 字符数：指的是字符的个数&…...
git提交信息写错处理方式
在Git中，你可以通过使用rebase命令来合并提交记录。以下是一个简单的步骤来合并一系列提交： 使用git rebase -i开始交互式变基。在打开的编辑器中，你会看到一个提交列表。若要合并提交，将要合并的提交前面的pick改为squash或s。保…...
C#从零开始学习(用unity探索C#)(unity Lab1)
初次使用Unity 本章所有的代码都放在 https://github.com/hikinazimi/head-first-Csharp Unity的下载与安装 从 unity官网下载Unity Hub Unity的使用 安装后,注册账号,下载unity版本,然后创建3d项目 设置窗口界面布局 3D对象的创建 点击对象,然后点击Move Guzmo,就可以拖动…...
【SpringBoot】15 Echarts+Thymeleaf 绘制各种图表
Gitee仓库 https://gitee.com/Lin_DH/system 介绍 ECharts是百度开源的一个前端组件。它是一个使用 JavaScript 实现的开源可视化库，可以流畅的运行在 PC 和移动设备上，兼容当前绝大部分浏览器（IE8/9/10/11，Chrome，…...
` 方法)
深入浅出：JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出：JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中，随机数的生成看似简单，却隐藏着许多玄机。无论是生成密码、加密密钥，还是创建安全令牌，随机数的质量直接关系到系统的安全性。Jav…...
[10-3]软件I2C读写MPU6050 江协科技学习笔记（16个知识点）
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...
sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...
MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现（两者等价），用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例： 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...
Swagger和OpenApi的前世今生
Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章，二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑： 🔄 一、起源与初创期：Swagger的诞生（2010-2014） 核心…...
HarmonyOS运动开发：如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit（传感器服务）# 前言 在运动类应用中，运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据，如配速、距离、卡路里消耗等，用户可以更清晰…...
安宝特方案丨船舶智造的“AR+AI+作业标准化管理解决方案”（装配）
船舶制造装配管理现状：装配工作依赖人工经验，装配工人凭借长期实践积累的操作技巧完成零部件组装。企业通常制定了装配作业指导书，但在实际执行中，工人对指导书的理解和遵循程度参差不齐。 船舶装配过程中的挑战与需求 挑战 (1…...
智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展，AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术，在客户服务、营销推广、信息查询等领域发挥着越来越重要…...
根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的----NTFS源代码分析--重要
根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的 第一部分： 0: kd> g Breakpoint 9 hit Ntfs!ReadIndexBuffer: f7173886 55 push ebp 0: kd> kc # 00 Ntfs!ReadIndexBuffer 01 Ntfs!FindFirstIndexEntry 02 Ntfs!NtfsUpda…...
实战设计模式之模板方法模式
概述 模板方法模式定义了一个操作中的算法骨架，并将某些步骤延迟到子类中实现。模板方法使得子类可以在不改变算法结构的前提下，重新定义算法中的某些步骤。简单来说，就是在一个方法中定义了要执行的步骤顺序或算法框架，但允许子类…...