XML Schema 复合空元素
XML Schema 复合空元素
XML Schema 是一种用于定义 XML 文档结构和内容的语言。在 XML Schema 中,元素可以被定义为简单类型或复杂类型。简单类型元素不能包含其他元素或属性,而复杂类型元素可以包含其他元素、属性或两者都有。复合空元素是一种特殊类型的复杂元素,它不包含任何内容,但可以包含属性。
复合空元素的定义
在 XML Schema 中,复合空元素是通过在 complexType 元素内使用 empty 元素来定义的。例如:
<xsd:complexType name="myComplexType"><xsd:complexContent><xsd:restriction base="xsd:anyType"><xsd:attribute name="myAttribute" type="xsd:string" /></xsd:restriction></xsd:complexContent>
</xsd:complexType>
在这个例子中,myComplexType 是一个复合空元素,它包含一个名为 myAttribute 的属性,但不包含任何内容。
复合空元素的使用
复合空元素通常用于表示没有实际内容,但需要通过属性来传递信息的元素。例如,在 XML 表示一个数据库记录时,可以使用复合空元素来表示一个没有数据值的字段,但需要通过属性来传递字段的元数据。
<record><field name="id" type="integer">123</field><field name="name" type="string">John Doe</field><field name="active" type="boolean" />
</record>
在这个例子中,active 字段是一个复合空元素,它没有内容,但通过 type 属性来表示字段的类型。
总结
XML Schema 中的复合空元素是一种特殊类型的复杂元素,它不包含任何内容,但可以包含属性。复合空元素通常用于表示没有实际内容,但需要通过属性来传递信息的元素。通过在 complexType 元素内使用 empty 元素来定义复合空元素,可以有效地表示和处理 XML 文档中的特殊结构。
相关文章:

XML Schema 复合空元素
XML Schema 复合空元素 XML Schema 是一种用于定义 XML 文档结构和内容的语言。在 XML Schema 中,元素可以被定义为简单类型或复杂类型。简单类型元素不能包含其他元素或属性,而复杂类型元素可以包含其他元素、属性或两者都有。复合空元素是一种特殊类型…...

Java面向对象编程基础(二)
Java面向对象编程基础二 一、package与import关键字的使用1.说明2.包的作用3.JDK中主要的包4. import5.import关键字的使用 二、封装性1.为什么要封装?2.如何封装?3.作用4.权限修饰符的权限大小5.案例 三、构造器1 构造器的使用说明2 案例: 四、实例变量赋值过程1 …...

[PHP]重复的Notice错误信息
<?php $a []; var_dump($a[name]);执行结果: 原因: display_errors和error_reporting都打开了Notice错误信息...

2024年第四届“网鼎杯”网络安全大赛-赛前模拟训练
文章目录 网络安全(WEB)签到题WEB01WEB02 二进制漏洞安全(PWN)PWN01潜在的安全漏洞分析攻击步骤exp 逆向工程(REVERSE)REVERSE01代码分析重构密码 密码学(CRYPTO)CRYPTO01CRYPTO02 杂…...

AI金融攻防赛:YOLO理论学习及赛题进阶思路(DataWhale组队学习)
引言 大家好,我是GISer Liu😁,一名热爱AI技术的GIS开发者。本系列文章是我跟随DataWhale 2024年10月学习赛的AI金融攻防赛学习总结文档。本文主要讲解如何在金融场景凭证篡改检测中应用YOLO算法。我们将从模型概述、数据准备、训练流程以及模…...

Spring Security 基础配置详解(附Demo)
目录 前言1. 基本知识2. Demo3. 实战 前言 基本的Java知识推荐阅读: java框架 零基础从入门到精通的学习路线 附开源项目面经等(超全)【Java项目】实战CRUD的功能整理(持续更新) 1. 基本知识 HttpSecurity 是 Spri…...
代码随想录打卡Day1
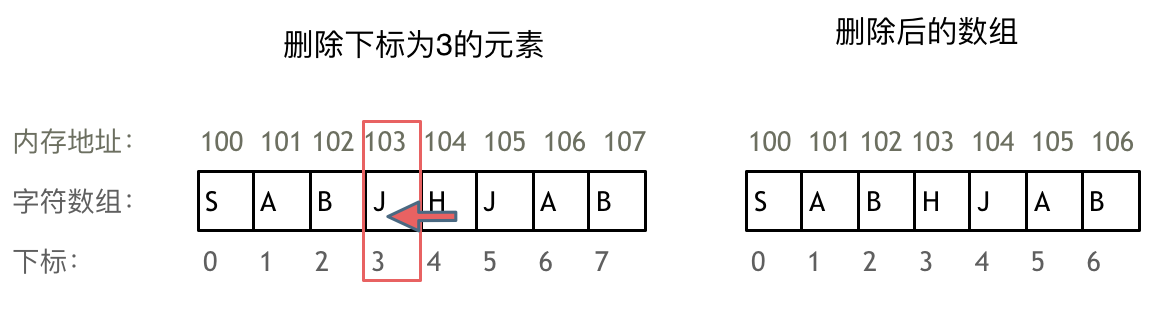
文章目录 day011 数组理论基础2 二分查找法3 移除元素4 平方数 day01 Java JDK是17.0.11 1 数组理论基础 数组是存放在连续内存空间上的相同类型数据的集合。 数组下标都是从0开始的。 数组内存空间的地址是连续的。 因为数组在内存空间的地址是连续的,所以我们…...

Vue快速创建工程+Element Plus
创建Vue工程 执行命令 npm init vuelatest 执行这两个绿色的命令 执行这个命令启动 npm run dev Element 打开网站https://element-plus.org/zh-CN/ npm install element-plus --save 然后在vscode中打开你的项目工程 // main.ts import { createApp } from vue import Ele…...

汽车管理系统——主界面制作
目录 主界面需要有什么?然后要做什么?添加两个主菜单(声明)下一步应该干什么?能够跳转到文件有哪几个动作?动作如何声明?为什么用选择声明指针,不选择直接声明这个对象? …...

C++ 右值引用深入理解:特性、优化与底层
目录 一、左右值的概念及右值的种类 二、左值引用与右值引用 左值引用给右值取别名: 右值引用给左值取别名: 三、引用的意义及左值引用的场景 四、移动构造: 右值引用在底层里的实现: 一、左右值的概念及右值的种类 在 C …...

C# 文件操作
文章目录 文件系统FileInfo和DirectoryInfo类完成一个文件的拷贝判断一个文件是否存在FileInfo和DirectoryInfo的属性列表FileInfo和DirectoryInfo的方法列表读写文件文件系统 下面的类用于浏览文件系统和执行操作,比如移动,复制和删除文件。 System.MarshalByRefObject 这个…...

FFmpeg 4.3 音视频-多路H265监控录放C++开发三 :安装QT5.14.2, 并将QT集成 到 VS2019中。
一,安装QT, 重点:在安装QT的时候要安装msvc201x版本的组件, 二 , 安装 qt-vs-tools Index of /development_releases/vsaddin/2.8.1 三,需要安装过 windows10 SDK,一般我们在安装vs2019的时候就…...

Linux 累加计算递归算法汇编实现
1...n可以使用公式计算,同时也是递归实现的很好例子,其c实现代码为 int f(int i) {i && (if(i-1));return i; } 其终止条件为0,此时i && (if(i-1))表达式不成立,不计算if(i-1)直接返回0&…...

明日周刊-第23期
十月已过半,气温也转凉了,大家注意保温哦。冬吃萝卜,夏吃姜,在快要到来的冬季大家可以选择多吃点萝卜。 配图是本周末去商场抓娃娃的时候拍的照片,现在抓娃娃单次普遍都控制在1块钱以下了,还记得多年前的抓…...

kubernets(二)
集群操作 查看集群信息 kubectl get查看各组件信息 格式:kubectl get 资源类型 【资源名】 【选项】 events #查看集群中的所有日志信息 -o wide # 显示资源详细信息,包括节点、地址... -o yaml/json #将当前资源对象输出至 yaml/json 格式文…...

《YOLO 标注工具全览》
《YOLO 标注工具全览》 一、YOLO 标注工具的重要性二、常见的 YOLO 标注工具介绍(一)LabelImg(二)Yolo_Label(三)在线标注工具 Make Sense(四)Ybat - YOLO BBox Annotation Tool&…...

财富思维学习
四大象限: 人类财富创造史经历的五个阶段: 1、黄色(土地)财务阶段:拥有土地和劳动力是财富的要求 2、蓝色(海)财富阶段:谁拥有贸易的通道谁就拥有财富(如港口ÿ…...
python爬虫加解密分析及实现
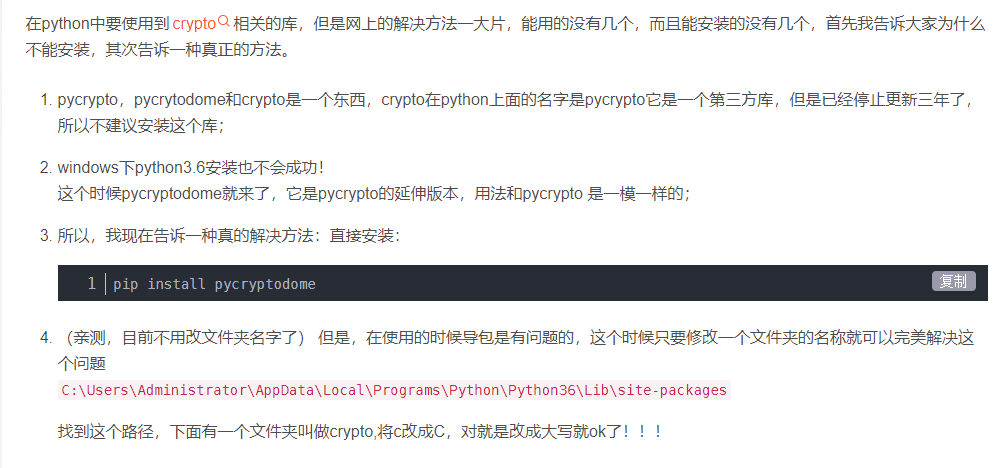
第一种: 1、找到加密的接口地址,通过加密的接口地址全局搜索 2、通过打断点的方式,操作页面,跑到断点处时,即可找到加密串,如图二; 3、找到用的是哪种加密方式,如: cr…...

用Java做智能客服,基于私有知识库
构建Java智能客服系统的整体思路 使用Java构建智能客服系统的整体思路是: 首先将客服QA文档以Word形式导入到系统中,通过向量化处理存入知识库。 当用户提出问题时,系统会根据问题内容从知识库中检索相关的上下文信息,并结合大…...
软考(网工)——网络安全
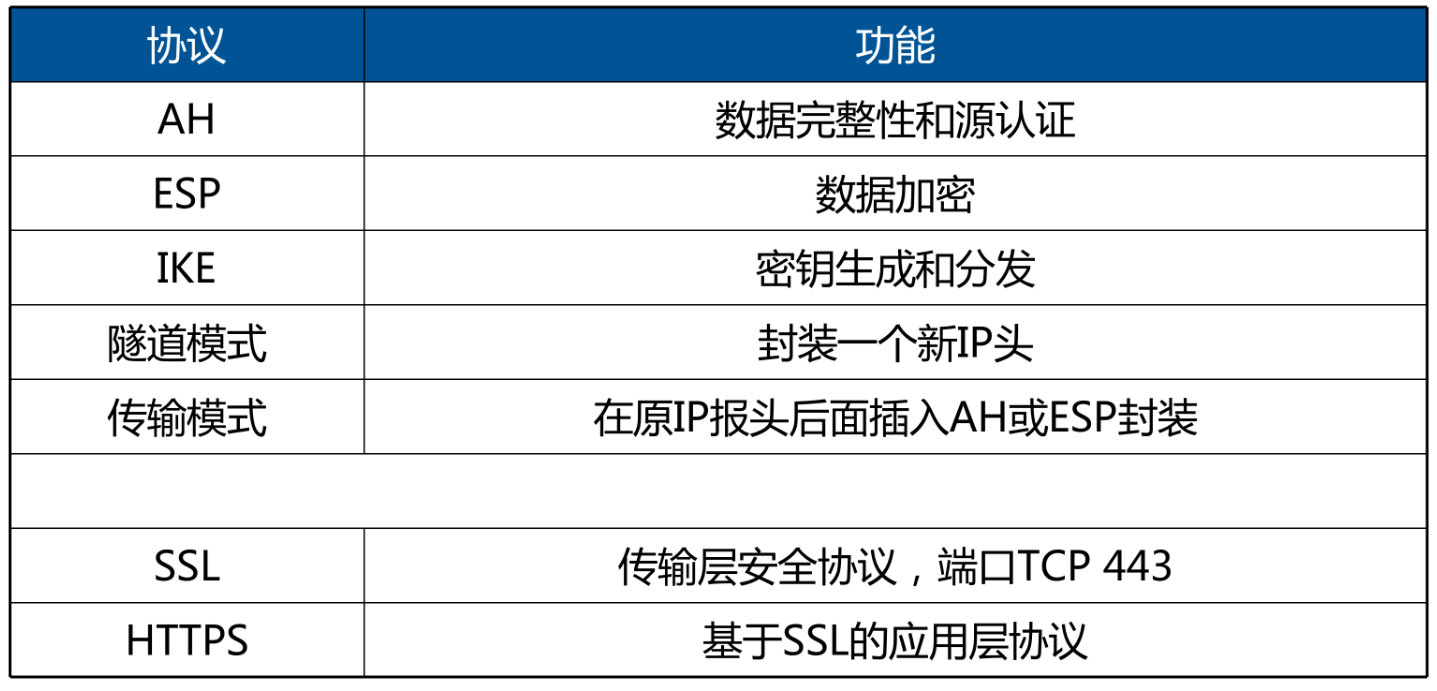
文章目录 🕐网络安全基础1️⃣网络安全威胁类型2️⃣网络攻击类型 🕑现代加密技术1️⃣私钥密码/对称密码体制2️⃣对称加密算法总结3️⃣公钥密码/非对称密码4️⃣混合密码5️⃣国产加密算法 - SM 系列6️⃣认证7️⃣基于公钥的认证 🕒Hash …...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...

Go语言多线程问题
打印零与奇偶数(leetcode 1116) 方法1:使用互斥锁和条件变量 package mainimport ("fmt""sync" )type ZeroEvenOdd struct {n intzeroMutex sync.MutexevenMutex sync.MutexoddMutex sync.Mutexcurrent int…...

三分算法与DeepSeek辅助证明是单峰函数
前置 单峰函数有唯一的最大值,最大值左侧的数值严格单调递增,最大值右侧的数值严格单调递减。 单谷函数有唯一的最小值,最小值左侧的数值严格单调递减,最小值右侧的数值严格单调递增。 三分的本质 三分和二分一样都是通过不断缩…...

离线语音识别方案分析
随着人工智能技术的不断发展,语音识别技术也得到了广泛的应用,从智能家居到车载系统,语音识别正在改变我们与设备的交互方式。尤其是离线语音识别,由于其在没有网络连接的情况下仍然能提供稳定、准确的语音处理能力,广…...

区块链技术概述
区块链技术是一种去中心化、分布式账本技术,通过密码学、共识机制和智能合约等核心组件,实现数据不可篡改、透明可追溯的系统。 一、核心技术 1. 去中心化 特点:数据存储在网络中的多个节点(计算机),而非…...

Python训练营-Day26-函数专题1:函数定义与参数
题目1:计算圆的面积 任务: 编写一个名为 calculate_circle_area 的函数,该函数接收圆的半径 radius 作为参数,并返回圆的面积。圆的面积 π * radius (可以使用 math.pi 作为 π 的值)要求:函数接收一个位置参数 radi…...
