光纤光学的基本方程

一、麦克斯韦方程与亥姆赫兹方程

1.1 麦克斯韦方程

光纤是一种介质光波导，具有以下特点：

① 无传导电流

② 无自由电荷

③ 线性各向同性

 推导出来的即为波动方程。为材料在真空中的磁导率，为材料在真空中的介电常数，n为材料折射率。

1.2 分离变量：电磁矢量分离

电场强度E的波动方程式

 该方程只与电场强度E有关，与磁场H无关。

1.3 分离变量：时空坐标分离

前提：光纤传播单色光波，时间函数为简谐函数

亥姆赫兹方程：

k-光纤中光波的波数 

二、程函方程与射线方程

2.1 程函方程：光程函数方程

 当已知折射率分布时，由程函方程可以求出光程函数 Q ，并进而由可求得光线的轨迹。

2.2 光线（射线）方程

设光线函数为S(x,y,z)，取线段元dS，dr 为dS的切线

 当光线与z 轴夹角很小时，有：

         将光线轨迹(由r描述)和空间折射率分布(n)联系起来; 由光线方程可以直接求出光线轨迹表达式; dr/dS是光线切向斜率, 对于均匀波导，n为常数,光线以直线形式传播;对于渐变波导,n是r的函数,则dr/dS为一变量,  这表明光线将发生弯曲。而且可以证明,光线总是向折射率高的区域弯曲。

典型光线传播轨迹：

三、模式分析的基本过程

3.1 数学模型

（1）阶跃折射率分布光纤(SIOF)是一种理想的数学模型,即认为光纤是一种无限大直圆柱系统,芯区半径a，折射率为n1；

（2）包层沿径向无限延伸,折射率为n2；  光纤材料

（3）为线性、无损、各向同性的电介质

（4）光纤是一种介质光波导，具有如下特点：①无传导电流； ②无自由电荷； ③线性各向同性。

3.2 变量分离：空间坐标纵横分离

波导场方程：

 

        是波动光学方法的最基本方程（χ和β分别是横向与纵向传播常数）。它是一个典型的本征方程，  其本征值为χ或β。当给定波导的边界条件时,求解波导场方程可得本征解及相应的本征值。通常将本征解定义为“模式”。

四、模式及其基本性质

4.1 模式

（1）每一个模式对应于沿光波导轴向传播的一种电磁波

（2）每一个模式对应于某一本征值并满足全部边界条件

（3）模式具有确定的相速群速和横场分布

（4）模式是波导结构的固有电磁共振属性的表征。给定的波导中能够存在的模式及其性质是已确定了的,外界激励源只能激励起光波导中允许存在的模式而不会改变模式的固有性质。(χ 和β及边界条件均由光纤本身决定，与外界激励源无关)

4.2 场的分布（本征解）

（1）模式场分布由六个场分量唯一决定

直角坐标系：Ex Ey Ez Hx Hy Hz  

圆柱坐标系：Er Ez  HrHz

Ez 和 Hz 总是独立满足波导场方程

场的横向分量可由纵向分量来表示——6个场分量可简化为2个纵向场分量的求解。

4.3 模式命名

根据场的纵向分量Ez和Hz的存在与否,可将模式命名为:

（1）横电磁模(TEM):Ez＝Hz＝0;  

（2）横电模(TE):Ez＝0, Hz≠0;  

（3）横磁模(TM):Ez≠0, Hz＝0;

（4）混杂模(HE或EH):Ez≠0, Hz≠0

光纤中存在的模式多数为HE(EH)模,有时也出现TE (TM) 模。

 4.4 纵向传播常数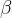（） 即与本征解相对应的本征值

z方向单位长度位相变化率; 波矢量k的z-分量

（1）实际上是等相位面沿z轴的变化率；

（2）数值分立，对应一组导模；

（3）不同的导模对应于同一个数值，我们称这些导模是简并的；

芯区：为实数；包层：为 纯虚数

4.5 归一化频率（V）

        给定光纤中,允许存在的导模由其结构参数所限定。光纤的结构参数可由其归一化频率V表征: V值越大，允许存在的导模数就越多。

导模的“截止”： 除了基模之外，其它导模都可能在某一个V值以下不允许存在。 这时导模转化为辐射模。使某一导模截止的Vc值称为导模的"截止条件"。

导模的“远离截止”： 当导模的本征值β→n1k0时,导模场紧紧束缚于纤芯中传输,称之为导模的“远离截止”。同样,每一个导模都对应于一合适的V值使其远离截止,称之为导模的“远离截止条件"。

 

4.6 横向传播常数（U、W）

横向分量：

对应于纤芯，对应于包层

定义横向传播常数：

场归一化传播常数：

 对应于纤芯，是实数；对应于包层，为纯虚数

U    —— 导模在芯区中的驻波场的横向振荡频率

W   —— 导模在包层中消逝场的衰减速度W， 越大，衰减越快

截止条件：W->0 场在包层中不衰减，导模转化为辐射模,导模截止

远离截止条件：W-> 场在包层中不存在，导模被约束在纤芯中，约束最强，远离截止

4.7 相速度与群速度

相速度：场的等相位面沿z轴的传播速度

群速度：光脉冲或波包中心或光能量沿z轴的传播速度

在光纤中,Vp大于光速c/n1而Vg小于光速c/n1,并有如下关系式:

 Vp＝ c/(n1cosθz  )≥ c /n1

 Vg＝(c/ n1)cosθz ≤ c /n1  

其中θz是波矢K与z轴夹角。仅当θz＝0时才有Vp＝Vg＝c/n1。  不同的θz角相应于不同的导模,对应于不同的相速Vp和群速Vg。

4.8 色散与群延时

群延时：光脉冲行经单位长度距离所需时间。

不同频率引起光脉冲的展宽——色散。

色散：不同模式之间会产生不同的群延时，这种群延时引起的脉冲展宽。

偏振特性:光纤中除了一个分量外，其余分量很小或为0，呈现线偏振模

功率流:单位时间内通过波导横截面的总能量：

正交性:不同导模的波印亭矢量等于零。