C++深入探寻二叉搜索树:数据管理的智慧之选
✨✨小新课堂开课了,欢迎欢迎~✨✨
🎈🎈养成好习惯,先赞后看哦~🎈🎈
所属专栏:C++:由浅入深篇
小新的主页:编程版小新-CSDN博客
前言:
我们在前面已经学习过有关二叉树的相关知识,今天我们要学习的搜索二叉树和前面我们学习的普通树结构有什么区别呢,我们来一起看看为啥称搜索二叉树是数据管理的智慧之选吧。这里要介绍的是普通的二叉搜索树,像AVL树,红黑树这种特殊的二叉搜索树,我们单独放在一篇博客说明。
一.二叉搜索树的概念
二叉搜索树又称二叉排序树,它或者是一棵空树,或者是具有以下性质的二叉树:
- 若它的左子树不为空,则左子树上所有结点的值都小于等于根结点的值
- 若它的右子树不为空,则右子树上所有结点的值都大于等于根结点的值
- 它的左右子树也分别为二叉搜索树
示例:以下就是两棵二叉搜索树

注意:
二叉搜索树中可以支持插入相等的值,也可以不支持插入相等的值,具体看使用场景定义,后续我们学习map/set/multimap/multiset系列容器底层就是二叉搜索树,其中map/set不支持插入相等值,multimap/multiset支持插入相等值。
二.二叉搜索树的常见操作
2.1插入操作
插入的具体过程如下:
1. 树为空,则直接新增结点,赋值给root指针
2. 树不为空,按二叉搜索树性质,插入值比当前结点大往右走,插入值比当前结点小往左走,找到空位置,插入新结点。
3. 如果支持插入相等的值,插入值跟当前结点相等的值可以往右走,也可以往左走,找到空位置,插入新结点。(要注意的是要保持逻辑⼀致性,插⼊相等的值不要一会往右走,一会往左走)
上面的插入过程就保证了在完成插入操作后,这棵树仍然满足搜索二叉树的特点。

bool Insert(const K& key)
{//如果树为空,直接新增节点,赋值给_rootif (_root == nullptr){_root = new Node(key);return true;}//如果树不为空Node* parent = nullptr;//parent的存在就是为了插入的,我们要插入在parent的左孩子或者右孩子Node* cur = _root;//找到空位置,插入节点while (cur){//插入值比当前节点小,往左走if (key < cur->_key){parent = cur;cur = cur->_left;}else if (key > cur->_key)//插入值比当前节点大,往右走{parent = cur;cur = cur->_right;}else{return false;//我们不支持插入相同的值}}//找到了,cur就是当前要插入的位置cur = new Node(key);//判断是插入到parent的左边还是右边if (key < parent->_key){//往左走parent->_left = cur;}else{//往右走parent->_right = cur;}return true;}2.2查找操作
查找的具体过程如下:
1. 从根开始比较,查找x,x比根的值大则往右边走查找,x比根值小则往左边走查找。
2. 最多查找高度次,走到到空,还没找到,这个值不存在。
3. 如果不支持插入相等的值,找到x即可返回。
4. 如果支持插入相等的值,意味着有多个x存在,一般要求查找中序的第一个x。如下图,查找3,要找到1的右孩子的那个3返回。
通过上面的查找过程可以发现,我们查找一个元素,最多只需查找高度次就能得到结果,在一定条件下这个查找效率还是蛮不错的,但是当树严重不平衡时,查找效率就变得非常低。
我们来举个例子,如果搜索二叉树的插入顺序不当,可能会导致树变得严重不平衡,退化成链表结构。在这种情况下,查找操作的时间复杂O(N).

//实现的是不允许有相同值的搜索二叉树
bool Find(const K& key)
{Node* cur = _root;while (cur){if (key < cur->_key){//小于,往左走cur = cur->_left;}else if (key > cur->_key){//大于,往右走cur = cur->_right;}else//={return true;//找到了}}return false;//没找到
}2.3删除操作
首先查找元素是否在二叉搜索树中,如果不存在,则返回false。
如果查找元素存在则分以下四种情况分别处理:(假设要删除的结点为N)
1. 要删除结点N左右孩子均为空
2. 要删除的结点N左孩子为空,右孩子结点不为空
3. 要删除的结点N右孩子为空,左孩子结点不为空
4. 要删除的结点N左右孩子结点均不为空
对应以上四种情况的解决方案:
1. 把N结点的父亲对应孩子指针指向空,直接删除N结点(情况1可以当成2或者3处理,效果是一样的)
2. 把N结点的父亲对应孩子指针指向N的右孩子,直接删除N结点

3. 把N结点的父亲对应孩子指针指向N的左孩子,直接删除N结点

4. 无法直接删除N结点,因为N的两个孩子无处安放,只能用替换法删除。
找N左子树的值最大结点R(最右结点)或者N右子树的值最小结点R(最左结点)替代N,因为这两个结点中任意一个,放到N的位置,都满足二叉搜索树的规则。替代N的意思就是N和R的两个结点的值交换,转而变成删除R结点,R结点符合情况2或情况3,可以直接删除。


bool Erase(const K& key)
{Node* parent = nullptr;Node* cur = _root;while (cur){if (key < cur->_key){//小于,往左走parent = cur;cur = cur->_left;}else if (key > cur->_key){//大于,往右走parent = cur;cur = cur->_right;}else//找到了{//删除//左为空if (cur->_left == nullptr){//根节点要特殊考虑,根节点没有父亲if (cur == _root){_root = cur->_right;}else{if (parent->_left == cur)//要删除节点是parent的左孩子{parent->_left = cur->_right;//父亲对应孩子指针指向N的右孩子(左为空)}else//要删除节点是parent的右孩子{parent->_right = cur->_right;//父亲对应孩子指针指向N的右孩子(左为空)}}delete cur;//直接删除}else if (cur->_right == nullptr)//右为空{//根节点要特殊考虑,根节点没有父亲if (cur == _root){_root = cur->_left;}else{if (parent->_left == cur)//要删除节点是parent的左孩子{parent->_left = cur->_left;//父亲对应孩子指针指向N的左孩子(右为空)}else//要删除节点是parent的右孩子{parent->_right = cur->_left;//父亲对应孩子指针指向N的左孩子(右为空)}}delete cur;//直接删除}else{//左右都不为空,采用替换法//以找右子树最左节点为例Node* replaceparent = cur;Node* replace = cur->_right;while (replace->_left)//左为空{replaceparent = replace;replace = replace->_left;}//交换值cur->_key = replace->_key;//删除replace节点if (replaceparent->_left == replace)//要删除节点是replaceparent的左孩子{replaceparent->_left = replace->_right;// 父亲对应孩子指针指向N的右孩子(左为空)}else{replaceparent->_right = replace->_right;// 父亲对应孩子指针指向N的右孩子(左为空)}delete replace;}return true;}}return false;
}2.4二叉树搜索树实现代码
namespace key
{template<class K>//Binary Search Tree Nodestruct BSTNode{K _key;//树节点的数据BSTNode<K>* _left;//树节点的左孩子BSTNode<K>* _right;//树节点的右孩子BSTNode(const K& key)//初始化根节点:_key(key), _left(nullptr), _right(nullptr){}};template<class K>//Binary Search Treeclass BSTree{//两种重命名的方式//typedef BSTNode<K> Node;using Node = BSTNode<K>;public:bool Insert(const K& key){//如果树为空,直接新增节点,赋值给_rootif (_root == nullptr){_root = new Node(key);return true;}//如果树不为空Node* parent = nullptr;//parent的存在就是为了插入的,我们要插入在parent的左孩子或者右孩子Node* cur = _root;//找到空位置,插入节点while (cur){//插入值比当前节点小,往左走if (key < cur->_key){parent = cur;cur = cur->_left;}else if (key > cur->_key)//插入值比当前节点大,往右走{parent = cur;cur = cur->_right;}else{return false;//我们不支持插入相同的值}}//找到了,cur就是当前要插入的位置cur = new Node(key);//判断是插入到parent的左边还是右边if (key < parent->_key){//往左走parent->_left = cur;}else{//往右走parent->_right = cur;}return true;}bool Find(const K& key){Node* cur = _root;while (cur){if (key < cur->_key){//小于,往左走cur = cur->_left;}else if (key > cur->_key){//大于,往右走cur = cur->_right;}else//={return true;//找到了}}return false;//没找到}bool Erase(const K& key){Node* parent = nullptr;Node* cur = _root;while (cur){if (key < cur->_key){//小于,往左走parent = cur;cur = cur->_left;}else if (key > cur->_key){//大于,往右走parent = cur;cur = cur->_right;}else//找到了{//删除//左为空if (cur->_left == nullptr){//根节点要特殊考虑,根节点没有父亲if (cur == _root){_root = cur->_right;}else{if (parent->_left == cur)//要删除节点是parent的左孩子{parent->_left = cur->_right;//父亲对应孩子指针指向N的右孩子(左为空)}else//要删除节点是parent的右孩子{parent->_right = cur->_right;//父亲对应孩子指针指向N的右孩子(左为空)}}delete cur;//直接删除}else if (cur->_right == nullptr)//右为空{//根节点要特殊考虑,根节点没有父亲if (cur == _root){_root = cur->_left;}else{if (parent->_left == cur)//要删除节点是parent的左孩子{parent->_left = cur->_left;//父亲对应孩子指针指向N的左孩子(右为空)}else//要删除节点是parent的右孩子{parent->_right = cur->_left;//父亲对应孩子指针指向N的左孩子(右为空)}}delete cur;//直接删除}else{//左右都不为空,采用替换法//以找右子树最左节点为例Node* replaceparent = cur;Node* replace = cur->_right;while (replace->_left)//左为空{replaceparent = replace;replace = replace->_left;}//交换值cur->_key = replace->_key;//删除replace节点if (replaceparent->_left == replace)//要删除节点是replaceparent的左孩子{replaceparent->_left = replace->_right;// 父亲对应孩子指针指向N的右孩子(左为空)}else{replaceparent->_right = replace->_right;// 父亲对应孩子指针指向N的右孩子(左为空)}delete replace;}return true;}}return false;}//在类外无法直接访问_rootvoid InOrder(){_InOrder(_root);cout << endl;}private://中序遍历打印void _InOrder(Node* root){if (root == nullptr){return;}_InOrder(root->_left);cout << root->_key << " ";_InOrder(root->_right);}private:Node* _root = nullptr;};}三.二叉搜索树的性能分析
最优情况下,二叉搜索树为完全二叉树(或者接近完全二叉树),其高度为: O(log2 N)。
最差情况下,二叉搜索树退化为单支树(或者类似单支),其高度为: O( N)。

所以综合而言二叉搜索树增删查的时间复杂度为: O(N)。
那么这样的效率显然是无法满足我们需求的,我们后续需要继续讲解⼆叉搜索树的变形,平衡⼆叉搜索树:AVL树和红黑树,才能适用于我们在内存中存储和搜索数据。
另外需要说明的是,二分查找也可以实现 O(logN) 级别的查找效率,但是二分查找有两大缺陷: 1. 需要存储在支持下标随机访问的结构中,并且有序。
2. 插入和删除数据效率很低,因为存储在下标随机访问的结构中,插入和删除数据⼀般需要挪动数据。
这里也就体现出了平衡二叉搜索树的价值。我们后面一起了解。
四.二叉搜索树key和key/value使用场景
4.1 key搜索场景:
只有key作为关键码,结构中只需要存储key即可,关键码即为需要搜索到的值,搜索场景只需要判断key在不在。key的搜索场景实现的二叉树搜索树支持增删查,但是不支持修改,修改key破坏搜索树结构了。
场景1:小区无人值守车库,小区车库买了车位的业主车才能进小区,那么物业会把买了车位的业主的车牌号录入后台系统,车辆进入时扫描车牌在不在系统中,在则抬杆,不在则提示非本小区车辆,无法进入。
场景2:检查一篇英文文章单词拼写是否正确,将词库中所有单词放入二叉搜索树,读取问章中的单词,查找是否在二叉搜索树中,不在则波浪线标红线提示。
像我们在上面实现的二叉搜索树就满足key搜索场景。
4.2 key/value搜索场景:
每一个关键码key,都有与之对应的值value,value可以任意类型对象。树的结构中(结点)除了需要存储key还要存储对应的value,增/删/查还是以key为关键字走二叉搜索树的规则进行比较,可以快速查找到key对应的value。key/value的搜索场景实现的二叉树搜索树支持修改,但是不支持修改key,修改key破坏搜索树结构了,可以修改value。
场景1:简单中英互译字典,树的结构中(结点)存储key(英文)和vlaue(中文),搜索时输入英文,则同时查找到了英文对应的中文。
场景2:商场无人值车库,入口进场时扫描车牌,记录车牌和入场时间,出口离场时,扫描车牌,查找入场时间,用当前时间-入场时间计算出停车时长,计算出停车费用,缴费后抬杆,车辆离场。
场景3:统计一篇文章中单词出现的次数,读取⼀个单词,查找单词是否存在,不存在这个说明第一次出现,(单词,1),单词存在,则++单词对应的次数。
我们在原来实现的二叉搜索树的基础上做些简单的整改即可。
namespace key_value
{template<class K, class V>struct BSTNode{K _key;V _value;BSTNode<K, V>* _left;BSTNode<K, V>* _right;BSTNode(const K& key, const V& value):_key(key), _value(value), _left(nullptr), _right(nullptr){}};// Binary Search Tree// Key/valuetemplate<class K, class V>class BSTree{//typedef BSTNode<K> Node;using Node = BSTNode<K, V>;public:// 强制生成构造BSTree() = default;BSTree(const BSTree& t){_root = Copy(t._root);}BSTree& operator=(BSTree tmp){swap(_root, tmp._root);return *this;}~BSTree(){Destroy(_root);_root = nullptr;}bool Insert(const K& key, const V& value){if (_root == nullptr){_root = new Node(key, value);return true;}Node* parent = nullptr;Node* cur = _root;//找到空位置,插入节点while (cur){if (key < cur->_key){parent = cur;cur = cur->_left;}else if (key > cur->_key){parent = cur;cur = cur->_right;}else{return false;}}cur = new Node(key, value);if (key < parent->_key){parent->_left = cur;}else{parent->_right = cur;}return true;}Node* Find(const K& key){Node* cur = _root;while (cur){if (key < cur->_key){cur = cur->_left;}else if (key > cur->_key){cur = cur->_right;}else{return cur;//找到了}}return nullptr;}bool Erase(const K& key){Node* parent = nullptr;Node* cur = _root;while (cur){if (key < cur->_key){ parent = cur;cur = cur->_left;}else if (key > cur->_key){parent = cur;cur = cur->_right;}else{//删除//左为空if (cur->_left == nullptr){if (cur == _root){_root = cur->_right;}else{if (parent->_left == cur){parent->_left = cur->_right;}else{parent->_right = cur->_right;}}delete cur;}else if (cur->_right == nullptr)//右为空{if (cur == _root){_root = cur->_left;}else{if (parent->_left == cur){parent->_left = cur->_left;}else{parent->_right = cur->_left;}}delete cur;}else{//左右都不为空Node* replaceparent = cur;Node* replace = cur->_right;while (replace->_left)//左为空{replaceparent = replace;replace = replace->_left;}cur->_key = replace->_key;if (replaceparent->_left == replace){replaceparent->_left = replace->_right;}else{replaceparent->_right = replace->_right;}delete replace;}return true;}}return false;}void InOrder(){_InOrder(_root);cout << endl;}private:void _InOrder(Node* root){if (root == nullptr){return;}_InOrder(root->_left);cout << root->_key << ":" << root->_value << endl;_InOrder(root->_right);}void Destroy(Node* root){if (root == nullptr)return;Destroy(root->_left);Destroy(root->_right);delete root;}Node* Copy(Node* root){if (root == nullptr)return nullptr;Node* newRoot = new Node(root->_key, root->_value);newRoot->_left = Copy(root->_left);newRoot->_right = Copy(root->_right);return newRoot;}private:Node* _root = nullptr;};
};int main()
{string arr[] = { "苹果", "西瓜", "苹果", "西瓜", "苹果", "苹果", "西瓜","苹果", "香蕉", "苹果", "香蕉" };key_value::BSTree<string, int> countTree;for (const auto& str : arr){// 先查找水果在不在搜索树中// 1、不在,说明水果第一次出现,则插入<水果, 1>// 2、在,则查找到的结点中水果对应的次数++//BSTreeNode<string, int>* ret = countTree.Find(str);auto ret = countTree.Find(str);if (ret == nullptr){countTree.Insert(str, 1);}else{// 修改valueret->_value++;}}countTree.InOrder();key_value::BSTree<string, int> copy = countTree;copy.InOrder();return 0;
}总结:
二叉搜索树的基本特点及其使用场景我们已经介绍完了,还有一些知识点我们没提,我们后面先谈map/set/multimap/multiset系列容器,它们的底层就是二叉搜索树,之后再介绍平衡二叉搜索树:AVL树和红黑树。大家快来一起学习吧。
感谢各位大佬的观看,创作不易,还请各位大佬点赞支持~
相关文章:

C++深入探寻二叉搜索树:数据管理的智慧之选
✨✨小新课堂开课了,欢迎欢迎~✨✨ 🎈🎈养成好习惯,先赞后看哦~🎈🎈 所属专栏:C:由浅入深篇 小新的主页:编程版小新-CSDN博客 前言: 我们在前面已经学习过有关…...

Python 文件 I/O 入门指南
Python 文件 I/O 入门指南 文章目录 Python 文件 I/O 入门指南一、文件的打开与关闭二、文件的读取三、文件的写入四、文件的定位五、文件的属性六、处理不同类型的文件七、错误处理八、总结 在 Python 编程中,文件输入输出(I/O)是一项非常重…...

Atlas800昇腾服务器(型号:3000)—YOLO全系列NPU推理【检测】(五)
服务器配置如下: CPU/NPU:鲲鹏 CPU(ARM64)A300I pro推理卡 系统:Kylin V10 SP1【下载链接】【安装链接】 驱动与固件版本版本: Ascend-hdk-310p-npu-driver_23.0.1_linux-aarch64.run【下载链接】 Ascend-…...

1.2.3 TCP IP模型
TCP/IP模型(接网叔用) 网络接口层 网络层 传输层 应用层 理念:如果某些应用需要“数据格式转换”“会话管理功能”,就交给应用层的特定协议去实现 tip:数据 局部正确不等于全局正确 但是,数据的 全局正…...

选择、冒泡和插入排序及其优化版本课件
视频链接:是趣味编程的个人空间-是趣味编程个人主页-哔哩哔哩视频...

Matlab自学笔记三十九:日期时间型数据的算术运算:加减运算
1.说明 时间点和(日历)持续时间是可加的,结果是时间点;两个时间点是可减的,结果是持续时间,用时分秒表示;时间型和浮点数运算,结果是时间型,浮点数默认单位是天…...

Java-多线程2
什么是线程? 线程是 cpu调度和执行的单位。 多个线程共享进程的堆和方法区资源,但每个线程有自己的程序计数器、虚拟机栈和本地方法栈。 如何实现线程 继承Thread类 实现步骤: 创建自定义类,继承Thread类 重写run方法 创建自定…...
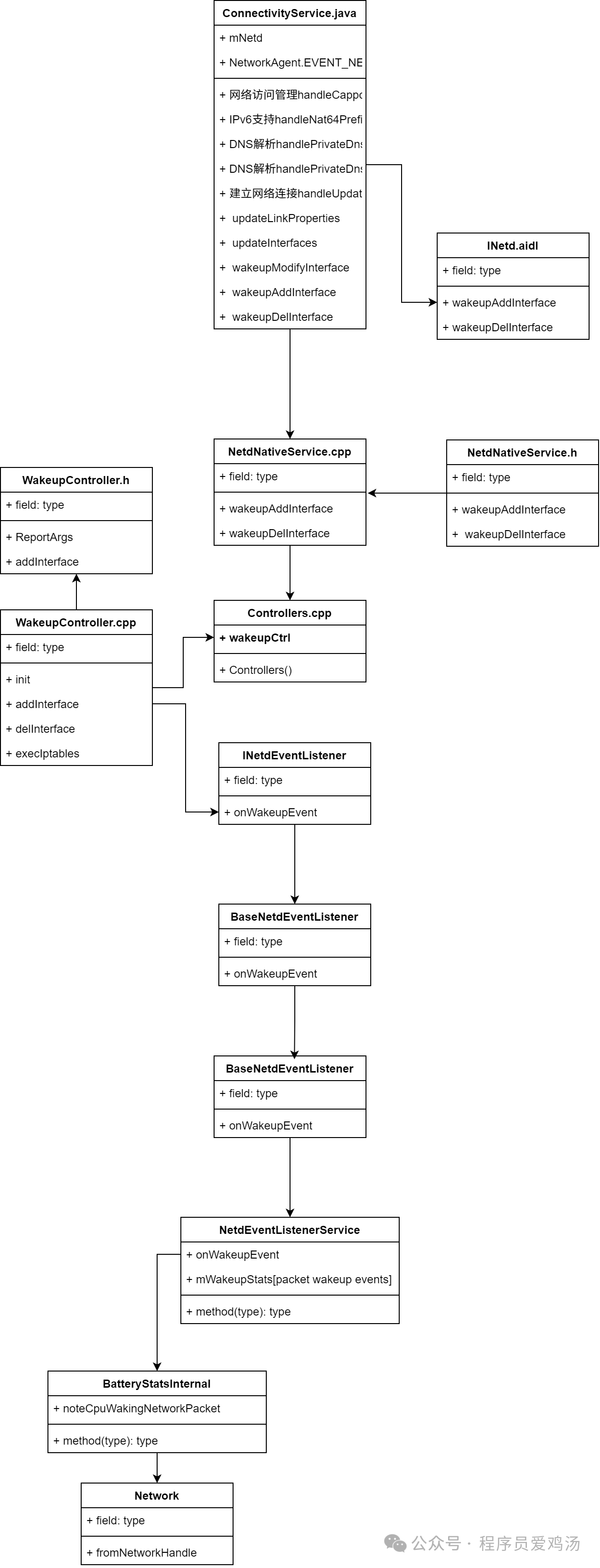
POWER_CONMETRICS的packet wakeup events触发条件的代码走读
摘要: adb shell dumpsys connmetrics 的packet wakeup events触发条件:首先App是无法控制packet wakeup events的事件日志打印,主要App联网过程中网络状态或配置发生变化时由系统netd自动触发的统计。 通俗理解:目前主要表示触…...

Bug:通过反射修改@Autowired注入Bean的字段,明确存在,报错 NoSuchFieldException
【BUG】通过Autowired注入了一个Bean SeqNo,测试的时候需要修改其中的字段。通过传统的反射,无论如何都拿不到信息,关键是一方面可以通过IDEA跳转,一方面debug也确实能看到这个字段。但是每次调用set方法报错:NoSuchFi…...
Vue项目兼容IE11
配置Vue项目兼容IE11详解 Vue 不支持 IE8 及以下版本,因为 Vue 使用了 IE8 无法模拟的 ECMAScript 5 特性。但对于 IE9,Vue 底层是支持。 由于开发过程中,我们经常会使用一些第三方插件或组件,对于这些组件,有时我们…...
可以帮助你快速禁用windows自带的防火墙程序defender control,有效解决占用内存大的问题,供大家学习研究参考
可以关闭windows自带的windows defender防火墙的工具,defender control官方版界面小巧,功能强大,当大家需要手动关闭或禁用windows defender时,就可以使用这款软件,以此来一键关闭或开启这个烦人的系统防火墙。操作起来也非常的简单便捷。 defender control怎么使用 下载…...

2024年9月电子学会Scratch图形化编程等级考试二级真题试卷
2024.09 Scratch图形化编程等级考试二级真题试卷 题目总数:37 总分数:100 一、选择题 第 1 题 Scratch小猫初始坐标是(50,50),小猫向下移动100步后的坐标是?( ) A.(150,50) B.(-50,50) C.(50,-50) D.(50,1…...

STL-vector+题目
vector-顺序表,可以存放任意类型的数据。 vector在[ ]和迭代器、范围for方面的使用差不多一样。 vector的迭代器有普通的还有const类型的迭代器。 vector使用下标[ ]好用。迭代器是容器通用的访问方式,使用方法基本相似。 #include <iostream> #i…...
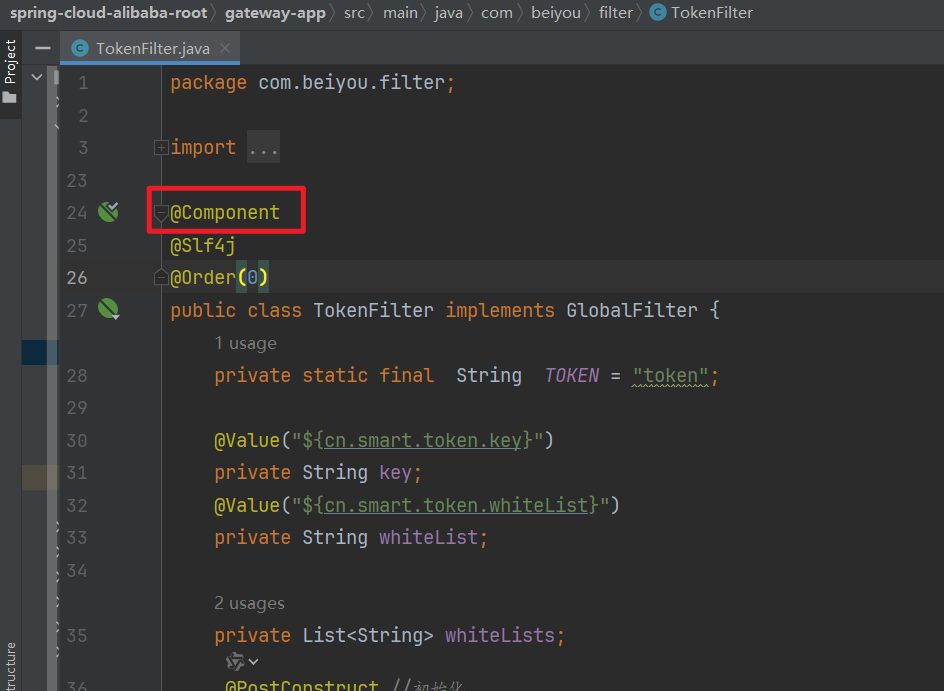
微服务--Gateway网关--全局Token过滤器【重要】
全局过滤器 GlobalFilter, 注入到 IOC里面即可 概念: 全局过滤器: 所有的请求 都会在执行链里面执行这个过滤器 如添加日志、鉴权等 创建一个全局过滤器的基本步骤: 步骤1: 创建过滤器类 首先,创建一个实现了Globa…...
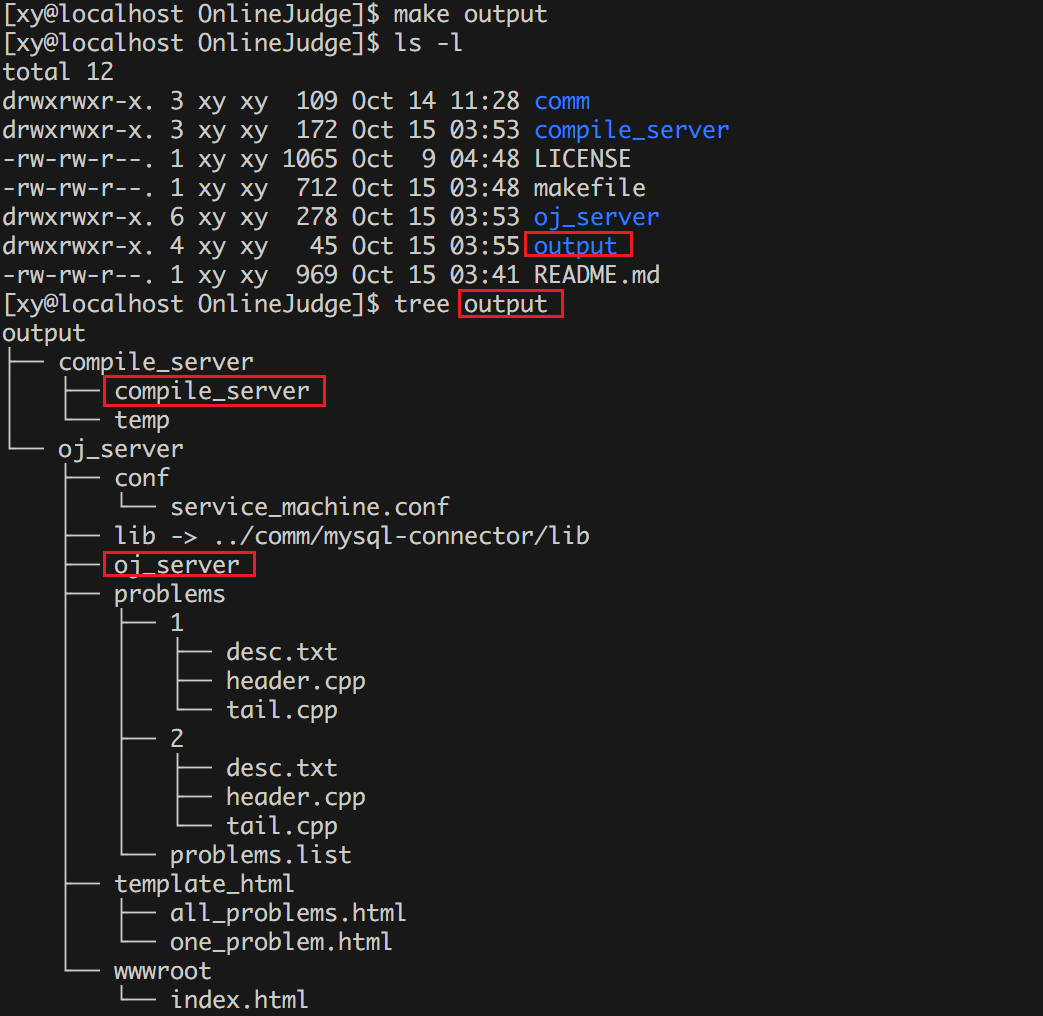
负载均衡在线判题系统【项目】
项目介绍 本项目是一个负载均衡的在线判题系统 (Online Judge, OJ) 的简易实现。该系统的核心功能是处理大量编程问题的提交,并通过负载均衡的机制,分配判题任务到多台服务器上,确保高效和可靠的评测。系统通过自动选择负载较低的服务器进行…...

重构复杂简单变量之用子类替换类型码
子类替换类型码 是一种用于将类型码替换为子类。当代码使用类型码(通常是 int、string 或 enum)来表示对象的不同类别,并且这些类别的行为有所不同时,使用子类可以更加清晰地表达这些差异并减少复杂的条件判断。 一、什么时候使用…...

【Nginx系列】Nginx配置超时时间
💝💝💝欢迎来到我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:kwan 的首页,持续学…...

2024年龙信
挂载VC的密码:MjAyNOmmeS/oeadrw 手机取证 1. Android 设备在通过 ADB 连接时,通常会要求用户授权连接,会要求用户确认设备授权,并将该设备的公钥保存在 adb_keys文件中 寻找到data/misc/adb/adb_keys下面有中有两个,…...

PyCharm配置Flask开发环境
文章目录 一、步骤1.安装虚拟环境2.创建虚拟环境文件夹3.安装虚拟环境目录4.进入虚拟环境5.active命令 激活6.安装Flask7.在Pycharm中配置Flask环境 总结 一、步骤 1.安装虚拟环境 代码如下(示例): pip install virtualenv 或者 pip insta…...

【人工智能-初级】第2章 机器学习入门:从线性回归开始
文章目录 一、什么是线性回归?二、线性回归的基本概念2.1 一元线性回归2.2 多元线性回归 三、如何进行线性回归建模?四、用Python实现线性回归4.1 导入必要的库4.2 创建虚拟数据集4.3 数据可视化4.4 拆分训练集和测试集4.5 训练线性回归模型4.6 查看模型…...

基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统,利用大模型实现智能 UI 自动化,结合计算机视觉和自然语言处理技术,实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...
)
云计算——弹性云计算器(ECS)
弹性云服务器:ECS 概述 云计算重构了ICT系统,云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台,包含如下主要概念。 ECS(Elastic Cloud Server):即弹性云服务器,是云计算…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...

3-11单元格区域边界定位(End属性)学习笔记
返回一个Range 对象,只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意:它移动的位置必须是相连的有内容的单元格…...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...


