2024_newstar_week1_crypto
baby_mod
题目
from Crypto.Util.number import *
from enc import flagm = bytes_to_long(flag)
p = getPrime(512)
q = getPrime(512)
r = getPrime(777)
t = getPrime(777)
tmp = getPrime(15)
e = 65537
n = p*q
print(f"c = {pow(m,e,n)}")
print(f"leak = {p*r-q*t-tmp}")
print(f"r = {r}")
print(f"t = {t}")
'''
c = 96982039932229986062184914601615337593043855203774154540088390154342582088831916489058244587175957104358890145287495969283908143946922141956046788682712898363783402241560976405970315671672552923522701316678810485294674195630815050476285989575640450156805391161033493965873279278988644128282368833511866391272
leak = -1180847553193702442682855971492433867077531621553705895665752944261387978020725138310978347411094960600631015411043321869598234964934461520124654252289173034818656892126034947337615252211847926165805347819958028791051889055142629057511345515311653746760688497024706371522772992776170510122534956283296780261674873647586541530925594367695865226079797779932907310916426415306226059601393833
r = 555797339419088018088392353722632677120529486185502253668037127566019016793303651597662002588421521808545398217688858573947882275827648269186472877116322039993971951402872097987262258339281612189840025558776368111961623523680175402251
t = 615237327593075592111714628640541559188263387826820275486949838611939171990255175077060052605716988822434177843980140335848735957800630838341686578454114569595081005934167126914965088689925981903197468471981207054308719385834371435283
'''
思路:
由题目获悉:
tmp比较小,所以可以通过遍历来找到tmp
已知p*r-q*t=tmp+leak
r,t已知,等号右边是已知的
前提知识:同余方程ax+b≡0 mod m 有解当且仅当(a,m) |b
其实这里可以转换成:p*r≡tmp+leak mod t 等式一
因为r和t都是素数,gcd(r,t)=1,满足求逆元的条件即
r*reverse_r≡1 mod t
reverse_r≡invert(r,t) mod t 等式二
等式一与等式二左右互相乘得到
p≡(tmp+leak)*invert(r,t) mod t
得到p后,正常RSA即可
脚本代码
from Crypto.Util.number import *
import gmpy2
import random
e=65537
c = 96982039932229986062184914601615337593043855203774154540088390154342582088831916489058244587175957104358890145287495969283908143946922141956046788682712898363783402241560976405970315671672552923522701316678810485294674195630815050476285989575640450156805391161033493965873279278988644128282368833511866391272
leak = -1180847553193702442682855971492433867077531621553705895665752944261387978020725138310978347411094960600631015411043321869598234964934461520124654252289173034818656892126034947337615252211847926165805347819958028791051889055142629057511345515311653746760688497024706371522772992776170510122534956283296780261674873647586541530925594367695865226079797779932907310916426415306226059601393833
r = 555797339419088018088392353722632677120529486185502253668037127566019016793303651597662002588421521808545398217688858573947882275827648269186472877116322039993971951402872097987262258339281612189840025558776368111961623523680175402251
t = 615237327593075592111714628640541559188263387826820275486949838611939171990255175077060052605716988822434177843980140335848735957800630838341686578454114569595081005934167126914965088689925981903197468471981207054308719385834371435283for i in range(2**14,2**15):if isPrime(i):m=i+leakreverse_r=gmpy2.invert(r,t)p=(m)*reverse_r%tq=(p*r-m)//tphi=(p-1)*(q-1)n=p*qtry:d=gmpy2.invert(e,phi)m=long_to_bytes(pow(c,d,n)).decode()print('m=',m)if "SHCTF" in m:print(m)breakexcept:print('error=',i)
d_known
题目
from Crypto.Util.number import *
from gmpy2 import*
from flag import flagm = bytes_to_long(flag)
p = getPrime(1024)
q = next_prime(p)
n = p * q
e = 0x10001
d = inverse(e, (p-1) * (q-1))
c = pow(m, e, n)
print(c)
print(d)'''
c = 8403005375036059507668949476573899369837076550693144629696007329133738521122588246908668180262007583822485069032471230229549770088907327492388166010486964325710415178606379749545343189793702142141767762980168940368804592747996874261288443645015850756539154813150178362722924342723559439994909937372080935730144313164028471482815902766596987410476536851653179862928574243638806370225834643622307886196327090667639015773736760975825026730042601141073120344825434342776953353880893841021796908686865952628635659489153801608107977991641511819655554954728559776830459369692383459501715070991568406261564744500687976022691
d = 1281547902553859084293414419691638897259210312435297418784234419527800281969029795243656339270541966215028646560597711203810636432840182193309150385941111722862919651864511924052800894612960620402770864208616639177876428714431968751785435983752685651775450406691250991111356087508576749134112503921935196726490012713717428813187789532934984608690497645602362447401532583629361369243217877261931238807810829854090482021242655140085436883719126264624674661878500582573099068229419791284814598160647661913954583323359110846608678647386673439063560883714693030315336131614665692294033299011254428100383418733928067811833
'''思路:
这里只知道p和q的关系,如果我们能知道其中一个就很好做了,但我们p和q都不知道
我们知道两个素数之间间距大概不超过1500
如果我们能获得p和q中间的某个数,那是不是就能找到q
所以我们可以对n开平方根求出p和q中间的某个数x
常规的sqrt函数这里行不通,因为n数值太大
这里推荐一种牛顿法求平方根
def closest_integer_sqrt(n):if n == 0:return 0x = n // 2 # 初始猜测while True:new_x = (x + n // x) // 2if new_x >= x: # 当已有的估计接近真实平方根breakx = new_x# 此时 x 是接近 sqrt(n) 的整数# 检查 (x + 1) 是否更接近if (x + 1) ** 2 - n < n - x ** 2:return x + 1else:return x脚本代码
from Crypto.Util.number import *
from gmpy2 import*
import math
import decimaldef closest_integer_sqrt(n):if n == 0:return 0x = n // 2 # 初始猜测while True:new_x = (x + n // x) // 2if new_x >= x: # 当已有的估计接近真实平方根breakx = new_x# 此时 x 是接近 sqrt(n) 的整数# 检查 (x + 1) 是否更接近if (x + 1) ** 2 - n < n - x ** 2:return x + 1else:return xc=8403005375036059507668949476573899369837076550693144629696007329133738521122588246908668180262007583822485069032471230229549770088907327492388166010486964325710415178606379749545343189793702142141767762980168940368804592747996874261288443645015850756539154813150178362722924342723559439994909937372080935730144313164028471482815902766596987410476536851653179862928574243638806370225834643622307886196327090667639015773736760975825026730042601141073120344825434342776953353880893841021796908686865952628635659489153801608107977991641511819655554954728559776830459369692383459501715070991568406261564744500687976022691
d = 1281547902553859084293414419691638897259210312435297418784234419527800281969029795243656339270541966215028646560597711203810636432840182193309150385941111722862919651864511924052800894612960620402770864208616639177876428714431968751785435983752685651775450406691250991111356087508576749134112503921935196726490012713717428813187789532934984608690497645602362447401532583629361369243217877261931238807810829854090482021242655140085436883719126264624674661878500582573099068229419791284814598160647661913954583323359110846608678647386673439063560883714693030315336131614665692294033299011254428100383418733928067811833
e=65537for k in range(1,100000):if (e*d-1)%k==0:print(k)phi=(e*d-1)//kmiddle= closest_integer_sqrt(phi)q=gmpy2.next_prime(middle)try:if phi%(q-1)==0:p=phi//(q-1)+1n=p*qflag=long_to_bytes(pow(c,d,n)).decode()print(flag)breakexcept:continue相关文章:

2024_newstar_week1_crypto
baby_mod 题目 from Crypto.Util.number import * from enc import flagm bytes_to_long(flag) p getPrime(512) q getPrime(512) r getPrime(777) t getPrime(777) tmp getPrime(15) e 65537 n p*q print(f"c {pow(m,e,n)}") print(f"leak {p*r-q*…...
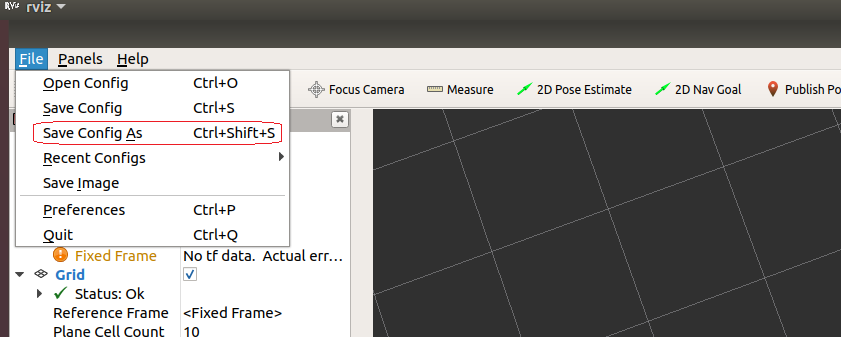
6.2 URDF集成Rviz基本流程
前面介绍过,URDF 不能单独使用,需要结合 Rviz 或 Gazebo,URDF 只是一个文件,需要在 Rviz 或 Gazebo 中渲染成图形化的机器人模型,当前,首先演示URDF与Rviz的集成使用,因为URDF与Rviz的集成较之于…...

双系统一体机电脑无法启动报错“Something has gone serously wrong: SBAT self-check failed: Security Policy Violation”
双系统一体机电脑无法启动 问题搜索解决办法解决开启时 F2 进入系统设置界面选择“疑难解答”选择“高级选项”选择“UEFI固件设置”进入“Start Menu”界面选择“Security”关闭相关选项 问题 在2024/8/14日Windows环境,系统更新了两个Windows更新项后,…...

八股面试2(自用)
mysql存储引擎 存储引擎:定义数据的存储方式,以及数据读取的实现逻辑 在以前数据库5.5默认MyISAM引擎,之后默认InnoDB引擎 MyISAM引擎的数据和索引是分开存储的,InnoDb将索引和文件存储在同一个文件。 MyISAM不支持事务&#…...

Leetcode 347 Top K Frequent Elements
题意: 求前k个出现频率最高的元素 首先得到一个频率图这是肯定的,下一步要考虑建立一个堆,堆中保存着前k个频率最大的数字,这个怎么做,可以用customized cmp来做,把数字存进去完事儿。注意这里不用 保存所有…...

[Linux网络编程]03-TCP协议
一.TCP协议数据通信的过程 TCP数据报如下,数据报中的标志位双端通信的关键。 三次握手: 1.客户端向服务端发送SYN标志位,请求建立连接,同时发送空包 2.服务端向客户端回发ACK标志位(即确认标志位,任何一端发送数据后都需要另一端…...

Windows和Linux在客户端/服务端在安全攻防方面的区别
Windows和Linux在客户端/服务端的安全攻防上存在一些显著区别,主要体现在系统架构、权限管理、安全工具、更新机制以及社区支持等方面。 一、系统架构与设计差异 1. 内核架构 Windows:Windows是一个闭源的操作系统,由微软开发和维护&#…...

VUE 仿神州租车-开放平台
项目背景: 神州租车是一家提供汽车租赁服务的公司,其API开放平台为开发者提供了访问神州租车相关服务和数据的接口。用VUE技术来仿照其开发平台。 成果展示: 首页: API文档: 关于我们:...
计算机的错误计算(一百二十九)
摘要 用错数解释计算机的错误计算(一百二十七)中的计算错误的原因。 从(一百二十七)知, 有四种形式: 四个 分别有1位、8位、8位、0位错误数字。 下面用错数解释前面3个错误计算的由来。 (1&a…...

process.platform 作用
process.platform 可以获取当前运行 Node.js 进程的操作系统平台的信息。 一、平台特定的代码执行 1. 适应不同操作系统 不同的操作系统可能有不同的行为、文件路径格式、命令行参数等。通过检查process.platform的值,可以根据当前运行的平台执行特定的代码逻辑。…...

Java项目-基于springboot框架的企业客户信息反馈系统项目实战(附源码+文档)
作者:计算机学长阿伟 开发技术:SpringBoot、SSM、Vue、MySQL、ElementUI等,“文末源码”。 开发运行环境 开发语言:Java数据库:MySQL技术:SpringBoot、Vue、Mybaits Plus、ELementUI工具:IDEA/…...

《深度学习》dlib 人脸应用实例 仿射变换 换脸术
目录 一、仿射变换 1、什么是仿射变换 2、原理 3、图像的仿射变换 1)图像的几何变换主要包括 2)图像的几何变换主要分为 1、刚性变换: 2、仿射变换 3、透视变换 3)常见仿射变换 二、案例实现 1、定义关键点索引 2、定…...

springboot044美容院管理系统(论文+源码)_kaic
本科毕业设计论文 题目:美容院管理系统设计与实现 系 别: XX系(全称) 专 业: 软件工程 班 级: 软件工程15201 学生姓名: 学生学号: 指导教师: 导师…...

大数据新视界 --大数据大厂之数据脱敏技术在大数据中的应用与挑战
💖💖💖亲爱的朋友们,热烈欢迎你们来到 青云交的博客!能与你们在此邂逅,我满心欢喜,深感无比荣幸。在这个瞬息万变的时代,我们每个人都在苦苦追寻一处能让心灵安然栖息的港湾。而 我的…...

Erric Gamma 关于resuable code的采访
采访地址 The risk of speculating Bill Venners: The GoF book says, “The key to maximizing reuse lies in anticipating new requirements and changes to existing requirements, and in designing your systems so they can evolve accordingly. To design a system s…...

【Ubuntu18.04命令行code打不开】可能的解决方法
目录 问题:命令行code打不开文件尝试① kimi是这么说的② sudo apt-get install apparmor apparmor_utils③ 在混沌的操作完以上一通后,sudo apt-get install snapd 我试了将近一个小时 : ( so depressed 我只是想用vscode打开个文件夹,我甚至…...

大数据毕业设计基于springboot+Hadoop实现的豆瓣电子图书推荐系统
文章目录 前言项目介绍技术介绍功能介绍核心代码数据库参考 系统效果图 前言 文章底部名片,获取项目的完整演示视频,免费解答技术疑问 项目介绍 随着开数字化阅读的普及,豆瓣电子图书推荐系统应运而生,旨在为用户提供个性化的阅…...
-- 人脸识别 -- EigenFaces算法)
【进阶OpenCV】 (15)-- 人脸识别 -- EigenFaces算法
文章目录 EigenFaces算法一、算法原理二、算法流程三、算法特点四、代码步骤1. 图像预处理2. 创建Eigenfaces人脸识别器3. 训练模型4. 预测图像 总结 EigenFaces算法 EigenFaces算法是一种基于主成分分析(PCA)的人脸识别方法,其核心思想是通…...
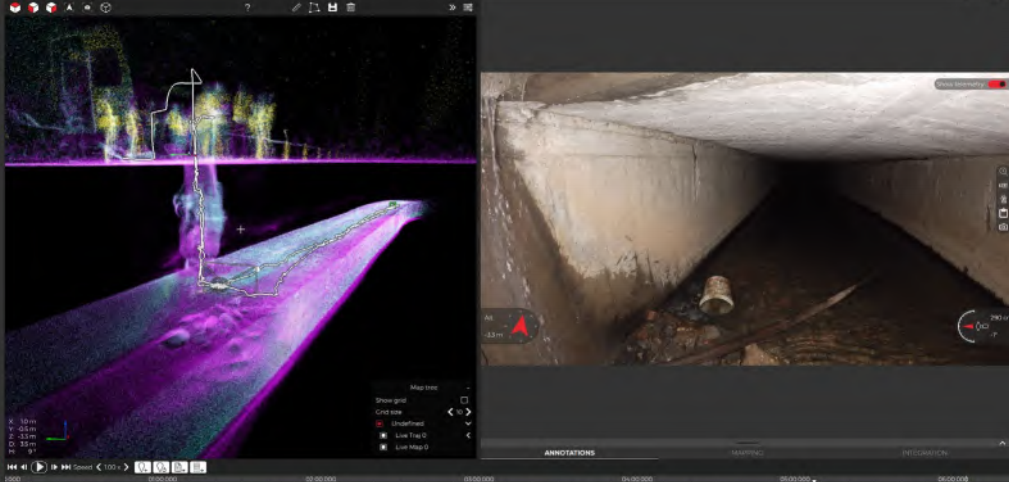
无人机封闭空间建图检测系统技术详解
无人机封闭空间建图检测系统技术是一种集成了多种传感器、智能算法与控制系统的高级技术,旨在实现无人机在复杂封闭环境下的自主导航、精确建图与高效检测。以下是对该技术的详细解析: 一、技术概述 无人机封闭空间建图检测系统通过集成激光雷达(LiDAR…...

webpack自定义插件 ChangeScriptSrcPlugin
插件文件 class ChangeScriptSrcPlugin {apply(compiler) {const pluginName "ChangeScriptSrcPlugin";compiler.hooks.compilation.tap(pluginName, (compilation, callback) > {compilation.hooks.htmlWebpackPluginAlterAssetTags.tapAsync(pluginName,(html…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

Linux 内存管理实战精讲:核心原理与面试常考点全解析
Linux 内存管理实战精讲:核心原理与面试常考点全解析 Linux 内核内存管理是系统设计中最复杂但也最核心的模块之一。它不仅支撑着虚拟内存机制、物理内存分配、进程隔离与资源复用,还直接决定系统运行的性能与稳定性。无论你是嵌入式开发者、内核调试工…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...
