每日算法一练:剑指offer——数组篇(3)
1.报数
实现一个十进制数字报数程序,请按照数字从小到大的顺序返回一个整数数列,该数列从数字 1 开始,到最大的正整数 cnt 位数字结束。
示例 1:
输入:cnt = 2
输出:[1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99]
1.1不考虑大数越界
题目要求打印 “从 1 至 cnt 的数字” ,最大的 cnt 位数(记为 end )和位数 cnt 的关系: 例如最大的 1 位数是 9 ,最大的 2 位数是 99 ,最大的 3 位数是 999 。则可推出公式:为10的cnt次方减去1。因此,只需定义区间 [1,10 cnt−1] 和步长 1 ,通过 for 循环生成结果列表 res 并返回即可。
class Solution {public int[] countNumbers(int cnt) {
//查询数组最大值。int end = (int)Math.pow(10, cnt) - 1;
//创建对应长度数组。int[] res = new int[end];
//依次存储。for(int i = 0; i < end; i++)res[i] = i + 1;return res;}
}1.2大数打印
实际上,本题的主要考点是大数越界情况下的打印。需要解决以下三个问题:
1. 表示大数的变量类型:
无论是 short / int / long ... 任意变量类型,数字的取值范围都是有限的。因此,大数的表示应用字符串 String 类型。
2. 生成数字的字符串集:
使用 int 类型时,每轮可通过 +1 生成下个数字,而此方法无法应用至 String 类型。并且, String 类型的数字的进位操作效率较低,例如 "9999" 至 "10000" 需要从个位到千位循环判断,进位 4 次。
观察可知,生成的列表实际上是 cnt 位 0 - 9 的 全排列 ,因此可避开进位操作,通过递归生成数字的 String 列表。
3. 递归生成全排列:
基于分治算法的思想,先固定高位,向低位递归,当个位已被固定时,添加数字的字符串。例如当 cnt=2 时(数字范围 1−99 ),固定十位为 0 - 9 ,按顺序依次开启递归,固定个位 0 - 9 ,终止递归并添加数字字符串。
复杂度分析:时间复杂度 O(10的cnt次方) : 递归的生成的排列的数量为 10的cnt次方。空间复杂度 O(10的cnt次方) 。结果列表 res 的长度为 10 cnt−1 ,各数字字符串的长度区间为 1,2,...,cnt ,因此占用 O(10 cnt) 大小的额外空间。
辅助函数 dfs(x, len) 的作用是:生成长度为len的数字,正在确定第 x 位。当 x=0 时表示左边第一位,不能为0,这样可以避免出现 0 开头的字符串。
代码实现:
class Solution {List<Integer> res; // 用于存储结果StringBuilder cur; // 当前生成的数字char[] NUM = {'0', '1', '2', '3', '4', '5', '6', '7', '8', '9'}; // 允许使用的数字// 生成长度为 len 的数字,正在确定第 x 位(从左往右)void dfs(int x, int len) {if (x == len) { // 递归终止条件:所有位数已经确定res.add(Integer.parseInt(cur.toString())); // 将当前数字加入结果集,转换为整数return;}int start = (x == 0) ? 1 : 0; // 如果是第一位数字,不能为 '0'for (int i = start; i < 10; i++) {cur.append(NUM[i]); // 确定当前位的数字dfs(x + 1, len); // 继续确定下一位cur.deleteCharAt(cur.length() - 1); // 回溯,删除本位数字}}public int[] countNumbers(int cnt) {res = new ArrayList<>(); // 初始化结果集cur = new StringBuilder(); // 初始化当前数字生成器for (int i = 1; i <= cnt; i++) { // 数字长度从 1 到 cntdfs(0, i); // 生成长度为 i 的所有数字}// 将结果转换为数组int[] resultArray = new int[res.size()];for (int i = 0; i < res.size(); i++) {resultArray[i] = res.get(i);}return resultArray; // 返回结果数组}
}1.3总结
本题主要考察大数越界,即用string来表示数组,且用递归生成全排列来生成数组。
2.训练计划I
2.1双线指针
教练使用整数数组 actions 记录一系列核心肌群训练项目编号。为增强训练趣味性,需要将所有奇数编号训练项目调整至偶数编号训练项目之前。请将调整后的训练项目编号以 数组 形式返回。
示例 1:
输入:actions = [1,2,3,4,5]
输出:[1,3,5,2,4]
解释:为正确答案之一
提示:
0 <= actions.length <= 500000 <= actions[i] <= 10000
考虑定义双指针 i , j 分列数组左右两端,循环执行:
指针 i 从左向右寻找偶数;
指针 j 从右向左寻找奇数;
将 偶数 actions[i] 和 奇数 actions[j] 交换。
可始终保证: 指针 i 左边都是奇数,指针 j 右边都是偶数 。
时间复杂度 O(N) : N 为数组 actions 长度,双指针 i, j 共同遍历整个数组。空间复杂度 O(1) : 双指针 i, j 使用常数大小的额外空间。
代码实现:
class Solution {public int[] trainingPlan(int[] actions) {
//定义两个指针,分别指向首尾两端。int i = 0, j = actions.length - 1, tmp;
//确保指针顺序while(i < j) {
//确保指针指向需调换元素上。while(i < j && (actions[i] & 1) == 1) i++;while(i < j && (actions[j] & 1) == 0) j--;
//若指到同一位置,互换无影响。tmp = actions[i];actions[i] = actions[j];actions[j] = tmp;}return actions;}
}
2.2 总结
题主要考察双向指针的灵活运用,其中要注意判断条件的选取。
3.库存管理II
仓库管理员以数组 stock 形式记录商品库存表。stock[i] 表示商品 id,可能存在重复。请返回库存表中数量大于 stock.length / 2 的商品 id。
示例 1:
输入: stock = [6, 1, 3, 1, 1, 1]
输出: 1
限制:
1 <= stock.length <= 50000- 给定数组为非空数组,且存在结果数字
3.1哈希表统计法
遍历数组 stock ,用 HashMap 统计各数字的数量,即可找出 众数 。此方法时间和空间复杂度均为 O(N) 。
代码实现:
class Solution {public int inventoryManagement(int[] stock) {// 创建一个 HashMap 来存储元素和它们的出现次数Map<Integer, Integer> map = new HashMap<>();// 计算数组长度的一半,用于判断某元素是否出现超过一半int n = stock.length / 2;// 遍历数组中的每一个元素for (int num : stock) {// 统计每个元素的出现次数,如果元素不在 map 中,则默认次数为 0map.put(num, map.getOrDefault(num, 0) + 1);// 如果某个元素的次数超过数组长度的一半,返回该元素if (map.get(num) > n)return num;}// 如果没有找到符合条件的元素,返回 0return 0;}
}
3.2数组排序法
将数组 stock 排序,数组中点的元素 一定为众数。时间复杂度: O(NlogN),因为排序的时间复杂度是 O(NlogN)。空间复杂度: O(1)(对于原地排序),或者 O(N)(取决于排序算法实现)。
class Solution {public int inventoryManagement(int[] stock) {// 首先对数组进行排序Arrays.sort(stock);// 返回数组中间的元素,众数一定在中间位置return stock[stock.length / 2];}
}3.3摩尔投票法
核心理念为 票数正负抵消 。此方法时间和空间复杂度分别为 O(N) 和 O(1) ,为本题的最佳解法。
摩尔投票法:
设输入数组 stock 的众数为 x ,数组长度为 n 。
推论一: 若记 众数 的票数为 +1 ,非众数 的票数为 −1 ,则一定有所有数字的 票数和 >0 。
推论二: 若数组的前 a 个数字的 票数和 =0 ,则 数组剩余 (n−a) 个数字的 票数和一定仍 >0 ,即后 (n−a) 个数字的 众数仍为 x 。
摩尔投票法(Boyer-Moore Voting Algorithm)是一种用于寻找数组中众数的高效算法。众数是指在数组中出现次数超过数组长度一半的元素。该算法的主要特点是时间复杂度为 O(N)且空间复杂度为 O(1),非常适合处理这个问题。
算法原理
摩尔投票法的核心思想是利用计数来确定候选众数。具体步骤如下:
-
初始化:
- 定义一个变量
candidate来存储当前候选的众数,和一个count来记录候选众数的计数,初始值为 0。
- 定义一个变量
-
遍历数组:
- 对于数组中的每个元素:
- 如果
count为 0,更新candidate为当前元素,并将count设为 1。 - 如果当前元素等于
candidate,则count加 1。 - 如果当前元素不等于
candidate,则count减 1。
- 如果
- 对于数组中的每个元素:
-
返回结果:
- 因为题目保证存在众数,所以在结束遍历后,
candidate就是众数。
- 因为题目保证存在众数,所以在结束遍历后,
代码实现:
class Solution {public int inventoryManagement(int[] stock) {// 变量 x 用于存储当前认为的候选众数,votes 用于统计支持度,count 用于验证候选众数的出现次数int x = 0, votes = 0, count = 0;// 第一遍历,找出候选众数for (int num : stock) {// 如果当前支持度为 0,则更新候选众数为当前元素 numif (votes == 0)x = num;// 更新支持度:如果 num 与候选众数相同,支持度加 1;否则减 1votes += (num == x) ? 1 : -1;}// 第二遍历,验证候选众数 x 是否为真正的众数for (int num : stock)// 统计候选众数 x 的出现次数if (x == num)count++;// 如果候选众数的出现次数大于数组长度的一半,则返回众数 x;否则返回 -1(表示无众数)return count > (stock.length / 2) ? x : -1;}
}
4.总结
本题主要考察寻找中位数中的摩尔投票法,该方法可提高算法性能。
4.库存管理III
仓库管理员以数组 stock 形式记录商品库存表,其中 stock[i] 表示对应商品库存余量。请返回库存余量最少的 cnt 个商品余量,返回 顺序不限。
示例 1:
输入:stock = [2,5,7,4], cnt = 1
输出:[2]
示例 2:
输入:stock = [0,2,3,6], cnt = 2
输出:[0,2] 或 [2,0]
提示:
0 <= cnt <= stock.length <= 10000
0 <= stock[i] <= 10000
4.1快速排序法
本题使用排序算法解决最直观,对数组 stock 执行排序,再返回前 cnt 个元素即可。
快速排序(Quick Sort)是一种高效的排序算法,采用分治法(Divide and Conquer)策略,通过一个称为“基准”(pivot)的元素将数组分为两个子数组,然后递归地对这两个子数组进行排序。快速排序的平均时间复杂度为 O(NlogN),但最坏情况下为 O(N^2)。空间复杂度 O(N) : 快速排序的递归深度最好(平均)为 O(logN) ,最差情况(即输入数组完全倒序)为 O(N)。
算法原理
-
选择基准:从数组中选择一个元素作为基准(pivot),可以选择第一个元素、最后一个元素或随机选择。
-
分区操作:重新排列数组,将比基准小的元素放到基准的左边,将比基准大的元素放到右边。经过分区后,基准元素在其最终位置上。
-
递归排序:对基准左边和右边的子数组递归进行快速排序。
-
终止条件:当子数组的大小为 0 或 1 时,表示该子数组已经排好序,递归结束。
代码实现:
class Solution {public int[] inventoryManagement(int[] stock, int cnt) {quickSort(stock, 0, stock.length - 1); // 调用快速排序return Arrays.copyOf(stock, cnt); // 返回前 cnt 个库存项}private void quickSort(int[] stock, int l, int r) {// 子数组长度为 1 时终止递归if (l >= r) return;// 哨兵划分操作(以 stock[l] 作为基准数)int i = l, j = r;while (i < j) {while (i < j && stock[j] >= stock[l]) j--; // 从右向左找到第一个小于基准数的元素while (i < j && stock[i] <= stock[l]) i++; // 从左向右找到第一个大于基准数的元素swap(stock, i, j); // 交换这两个元素}swap(stock, i, l); // 把基准数放到它最终的位置// 递归左(右)子数组执行哨兵划分quickSort(stock, l, i - 1); // 对左子数组排序quickSort(stock, i + 1, r); // 对右子数组排序}private void swap(int[] stock, int i, int j) {int tmp = stock[i]; // 交换元素stock[i] = stock[j];stock[j] = tmp;}
}
4.2快速选择法
根据给出的题目要求,我们需要返回库存余量最少的 cnt 个商品余量,且返回顺序不限。可以使用快速选择算法(Quick Select)来高效地实现这个目标。以下是实现的详细步骤和代码。
算法原理
-
选择基准:在数组中选择一个基准元素(可以选择最后一个元素)。
-
哨兵划分:对数组进行哨兵划分,将小于等于基准的元素放在基准的左侧,将大于基准的元素放在右侧。
-
判断基准位置:
- 每次划分后检查基准元素的索引。
- 如果基准元素的索引正好等于
cnt,则返回数组中前cnt个元素。 - 如果基准元素的索引小于
cnt,则说明最小的cnt个数在基准的右侧,需要对右侧部分继续进行划分。 - 如果基准元素的索引大于
cnt,则说明最小的cnt个数在基准的左侧,需要对左侧部分继续进行划分。
本方法优化时间复杂度的本质是通过判断舍去了不必要的递归(哨兵划分)。时间复杂度 O(N) : 其中 N 为数组元素数量;对于长度为 N 的数组执行哨兵划分操作的时间复杂度为 O(N) ;空间复杂度 O(logN) : 划分函数的平均递归深度为 O(logN) 。
代码实现:
class Solution {// 主方法:返回库存余量最少的 cnt 个商品余量public int[] inventoryManagement(int[] stock, int cnt) {// 如果 cnt 大于等于数组长度,直接返回整个数组if (cnt >= stock.length) return stock;// 调用快速选择方法,寻找最小的 cnt 个商品余量return quickSort(stock, cnt, 0, stock.length - 1);}// 辅助方法:快速选择算法,用于找到最小的 cnt 个元素private int[] quickSort(int[] stock, int cnt, int l, int r) {// 初始化左右指针int i = l, j = r;// 哨兵划分过程while (i < j) {// 从右向左,找到第一个小于基准元素的元素while (i < j && stock[j] >= stock[l]) j--;// 从左向右,找到第一个大于基准元素的元素while (i < j && stock[i] <= stock[l]) i++;// 交换这两个元素swap(stock, i, j);}// 交换基准元素到正确的位置swap(stock, i, l);// 判断基准元素的位置if (i > cnt) {// 如果基准元素位置大于 cnt,继续在左侧查找return quickSort(stock, cnt, l, i - 1);}if (i < cnt) {// 如果基准元素位置小于 cnt,继续在右侧查找return quickSort(stock, cnt, i + 1, r);}// 如果基准位置等于 cnt,返回前 cnt 个最小的元素return Arrays.copyOf(stock, cnt);}// 交换数组中两个元素的辅助方法private void swap(int[] stock, int i, int j) {int tmp = stock[i]; // 保存第一个元素的值stock[i] = stock[j]; // 将第二个元素赋值给第一个元素stock[j] = tmp; // 将保存的第一个元素值赋给第二个元素}
}
4.3总结
本题考查快速排序和快速选择两种高效的查找和选择算法。
相关文章:
)
每日算法一练:剑指offer——数组篇(3)
1.报数 实现一个十进制数字报数程序,请按照数字从小到大的顺序返回一个整数数列,该数列从数字 1 开始,到最大的正整数 cnt 位数字结束。 示例 1: 输入:cnt 2 输出:[1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,1…...

Java代码说明设计模式
以下是使用 Java 代码分别说明设计模式中的工厂模式、抽象工厂模式(这里推测你可能想说的是抽象工厂模式而非虚拟工厂模式)、建造者模式和观察者模式。 一、工厂模式 工厂模式是一种创建对象的设计模式,它提供了一种创建对象的方式…...
Golang笔记_day06
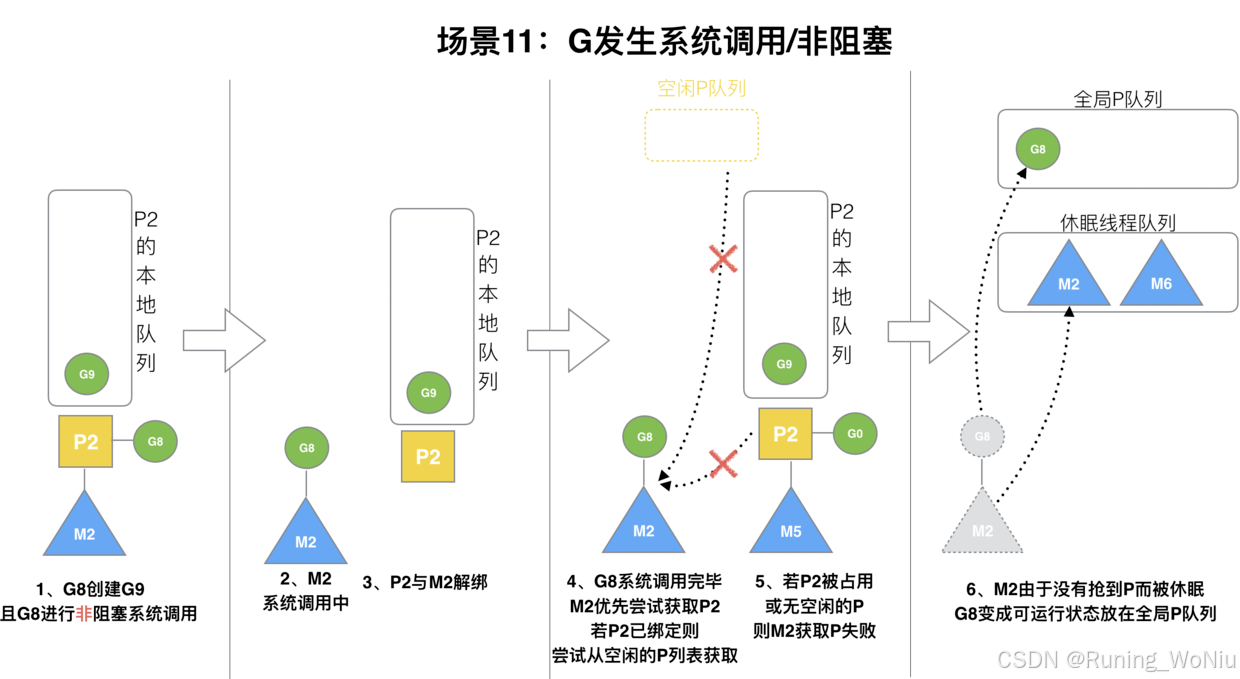
一、GMP 调度器 1、调度器理解思路 理解golang的调度器要从进程到协程演进来说明: 进程--->线程--->协程---> golang的协程(goroutine) 从上图可以看出,进程到多线程到协程,最终目的就是为了提高CPU的利用率…...
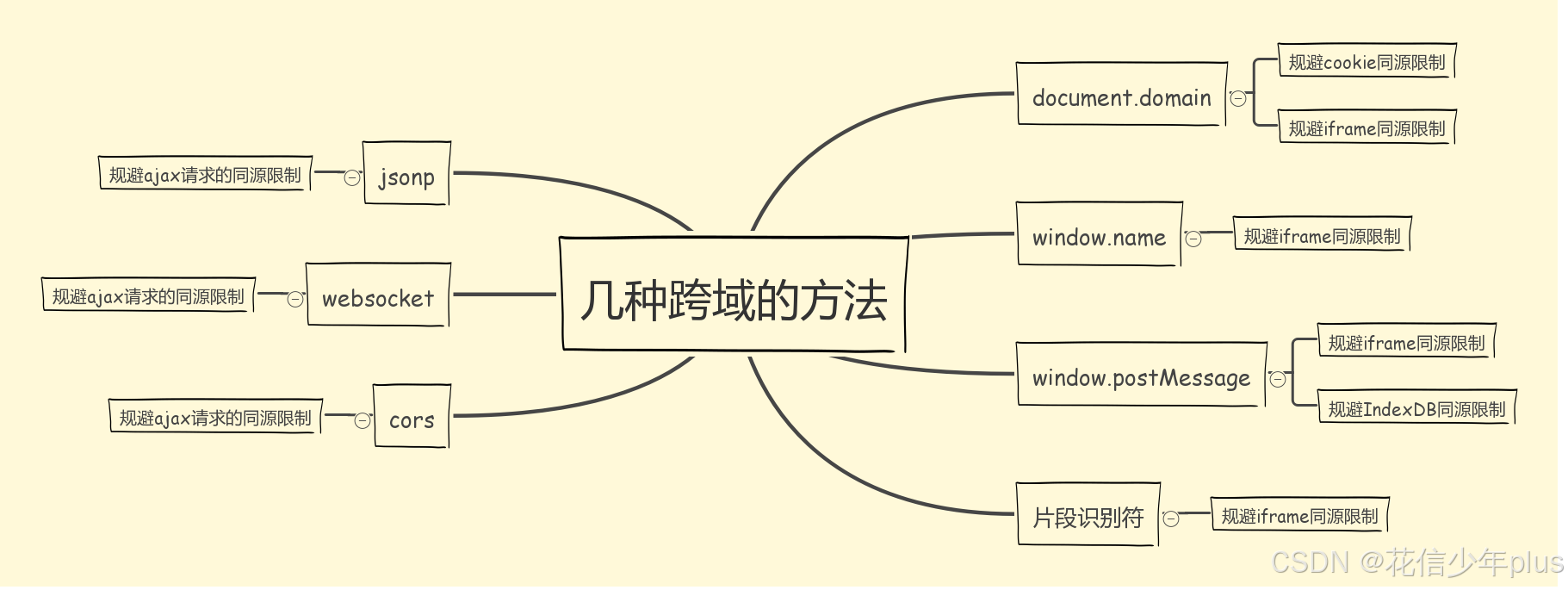
「从零开始的 Vue 3 系列」:第十一章——跨域问题解决方案全解析
前言 本系列将从零开始,系统性地介绍 Vue 3 的常用 API,逐步深入每个核心概念与功能模块。通过详尽的讲解与实战演示,帮助大家掌握 Vue 3 的基础与进阶知识,最终具备独立搭建完整 Vue 3 项目的能力。 第十一章:跨域问…...

C语言结构体数组 java静动数组及问题
1. (1)先声明,后定义:如上一天 //(2).声明时直接定义 #define N 5 typedef struct student { int num; int score; }STU; int main(void) { STU class3[N] { {10,90},{14,70},{8,95} }; …...
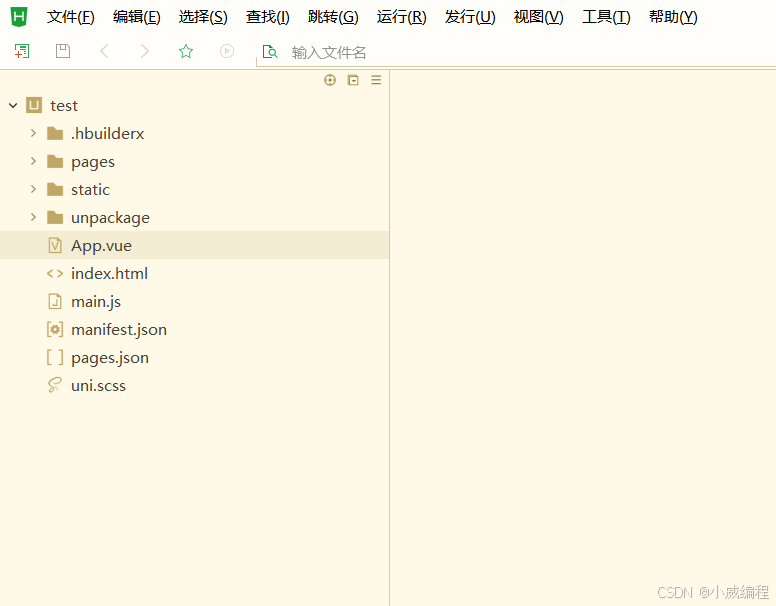
uniapp项目结构基本了解
基本结构的解释 App.vue:应用的根组件,定义全局布局和逻辑。pages/:存放各个页面的 .vue 文件,定义应用的具体页面和功能模块。main.js:应用入口文件,初始化应用,挂载 App.vue。manifest.json&…...

常见Web知识1
List item 常见Web知识1 JSON: JSON(JavaScript Object Notation)是一种轻量级的数据交换格式,易于人类阅读和编写,同时也易于机器解析和生成。它通常用于客户端和服务器之间的数据传输。 JSON 结构 JSON 主要由两…...
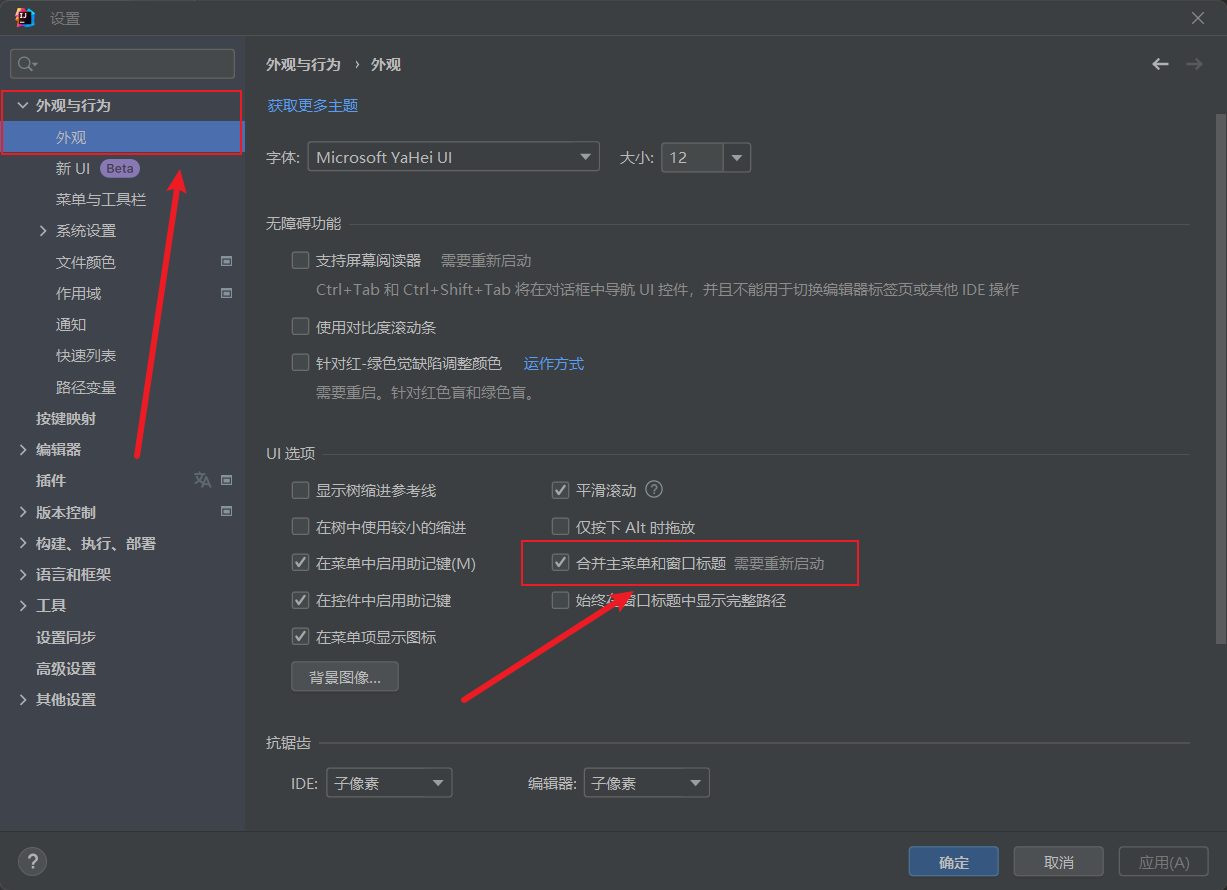
新版idea菜单栏展开与合并
新版idea把菜单栏合并了看着很是不习惯,找了半天原来在这里展开 ① 点击文件 -> 设置 ② 点击外观与行为 -> 外观 -> 合并主菜单和窗口标题 然后确定,重启即可...
聊聊Go语言的异常处理机制
背景 最近因为遇到了一个panic问题,加上之前零零散散看了些关于程序异常处理相关的东西,对这块有点兴趣,于是整理了一下golang对于异常处理的机制。 名词介绍 Painc golang的内置方法,能够改变程序的控制流。 当函数调用了pan…...

复习:如何理解 React 中的 fiber
React 中的 Fiber 可以理解为 React 16 引入的一种新的协调(reconciliation)引擎,旨在提高 React 应用的性能和响应性。以下是对 React Fiber 的详细解释: 一、Fiber 的定义与背景 Fiber 是对 React 核心算法的一次重新实现,它将渲染工作分解成一系列小的任务单元,这些任…...

10分钟了解腾讯云混元大模型AIGC系列产品
前言 其实说到AIGC,作为开发者,大家其实已经见怪不怪了,那么AIGC是什么,这里我再简单科普一下。 AIGC的全称是Artificial Intelligence Generated Content (人工智能生成内容)或者说叫生成式人工智能&…...

Unity发送Http
本篇实现在Unity中发送Http请求。 讲解Get,Post,用于在Unity中进行数据对接。 一、Get IEnumerator Get() {string url "";//链接UnityWebRequest request UnityWebRequest.Get(url);//创建UnityWebRequest实例并设置请求方式为Getyield …...

微服务开发-Nacos服务治理
注册中心原理 流程如下: 服务启动时就会注册自己的服务信息(服务名、IP、端口)到注册中心;调用者可以从注册中心订阅想要的服务,获取服务对应的实例列表(1个服务可能多实例部署);调…...

鸿蒙开发:两个重磅更新,鸿蒙版微信要来了!
从媒体消息中,其实我们已经知道,华为纯血鸿蒙系统(HarmonyOS NEXT)于10月8日正式开启了公测,对应的官方文档,大家可以看到已由原来的Beta版本更新到了Release,NEXT终于迎来了正式版本。 文档更新…...

es kibana .logstash离线集群安装
es离线集群安装 下载对应的版本一般看你客户端引用的是什么版本我这里下载的是7.6.2 官方下载地址:https://www.elastic.co/cn/downloads/elasticsearch 源码安装-环境准备:在etc/hosts文件添加3台主机 node-001 192.168.1.81 node-002 19…...

Java项目-基于springboot框架的基于协同过滤算法商品推荐系统项目实战(附源码+文档)
作者:计算机学长阿伟 开发技术:SpringBoot、SSM、Vue、MySQL、ElementUI等,“文末源码”。 开发运行环境 开发语言:Java数据库:MySQL技术:SpringBoot、Vue、Mybaits Plus、ELementUI工具:IDEA/…...

JAVA使用easyExcel导出数据到EXCEl,导出数据不全问题解决
JAVA使用easyExcel导出数据到EXCEl,导出数据不全问题解决 问题描述解决思路一解决思路二温馨提示 问题描述 JAVA使用easyExcel导出数据到EXCEl,导出数据不全问题。 导出的excel部分列有数据,好几列没有数据 解决思路一 从网上百度查询,大多数的解决思路…...

2-130 基于经验模态分解(EMD)的信号分解
基于经验模态分解(EMD)的信号分解。通过仿真信号构造待分解信号,经过分解后得到信号希尔伯特时频图,可视化展示不同分解信号频率段。程序已调通,可直接运行。 下载源程序请点链接:2-130 基于经验模态分解&…...
- vue3)
openlayers 测量功能实现(测距测面)- vue3
一、配置openlayer环境 借鉴:Vue 3 OpenLayers 的简单使用_vue3 openlayers-CSDN博客 二、代码如下(测距、测面和清除) measurs.js: import {ref} from vue; import Draw from ol/interaction/Draw import VectorSource from ol/source/…...
)
各种语言的序列化与反序列化(C/C++ c# Python Javascript Java)
序列化是指将程序中的对象转换为字节序列的过程,使得对象的状态可以在网络上传输或存储到文件中。反序列化则是将字节序列恢复为程序中的对象的过程。这两个过程是数据持久化和远程通信中的关键步骤。 1. C 序列化与反序列化 在 C 中,标准库没有提供内…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...

【Go语言基础【13】】函数、闭包、方法
文章目录 零、概述一、函数基础1、函数基础概念2、参数传递机制3、返回值特性3.1. 多返回值3.2. 命名返回值3.3. 错误处理 二、函数类型与高阶函数1. 函数类型定义2. 高阶函数(函数作为参数、返回值) 三、匿名函数与闭包1. 匿名函数(Lambda函…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...

Razor编程中@Html的方法使用大全
文章目录 1. 基础HTML辅助方法1.1 Html.ActionLink()1.2 Html.RouteLink()1.3 Html.Display() / Html.DisplayFor()1.4 Html.Editor() / Html.EditorFor()1.5 Html.Label() / Html.LabelFor()1.6 Html.TextBox() / Html.TextBoxFor() 2. 表单相关辅助方法2.1 Html.BeginForm() …...

R 语言科研绘图第 55 期 --- 网络图-聚类
在发表科研论文的过程中,科研绘图是必不可少的,一张好看的图形会是文章很大的加分项。 为了便于使用,本系列文章介绍的所有绘图都已收录到了 sciRplot 项目中,获取方式: R 语言科研绘图模板 --- sciRplothttps://mp.…...
