Python Numpy 实现神经网络自动训练:反向传播与激活函数的应用详解
Python Numpy 实现神经网络自动训练:反向传播与激活函数的应用详解
这篇文章介绍了如何使用 Python 的 Numpy 库来实现神经网络的自动训练,重点展示了反向传播算法和激活函数的应用。反向传播是神经网络训练的核心,能够通过计算梯度来优化模型参数,使得预测更加精准。文中详细演示了如何使用 Numpy 进行神经网络的前向预测、反向传播更新、误差计算,并通过引入 ReLU 等激活函数提升模型的非线性拟合能力。最后,通过对比训练前后的结果,展示了加入激活函数后模型性能的显著提升,适合初学者和爱好者学习神经网络的基础原理与应用。
文章目录
- Python Numpy 实现神经网络自动训练:反向传播与激活函数的应用详解
- 一 简单介绍反向传播
- 二 用 Numpy 来做神经网络
- 没有训练
- 开始训练
- 三 加入激活函数
- 常用激活函数
- 非线性计算,不加激活函数
- 非线性计算,加入激活函数
- 四 完整代码示例
- 五 源码地址
一 简单介绍反向传播
反向传播(Backpropagation)是训练神经网络的核心算法,用于通过计算损失函数相对于网络各个参数的梯度,逐步优化这些参数,从而使模型的预测结果更加准确。使用梯度反向更新规则做神经网络参数优化调整。
这段代码计算每一层神经层的更新幅度,让神经网络对数据拟合变好,不理解先当工具方法记住。
def backprop(dz, layer, layer_in, learning_rate=0.01):"""进行反向传播,更新当前层的权重和偏置,并计算传递给前一层的梯度。参数:dz: 当前层输出的梯度(损失函数对激活输出的偏导数)layer: 当前层的参数字典,包含权重 "w" 和偏置 "b"layer_in: 输入到当前层的激活值learning_rate: 学习率,用于控制参数更新的步长,默认值为 0.01返回:new_dz: 传递给前一层的梯度"""# 计算损失函数对权重的梯度,layer_in.T 是当前层输入的转置,dot(dz) 进行矩阵乘法gw = layer_in.T.dot(dz)# 计算损失函数对偏置的梯度,按列求和,保留维度,求得每个偏置的梯度gb = np.sum(dz, axis=0, keepdims=True)# 计算传递给前一层的梯度,使用当前层的权重转置与 dz 相乘new_dz = dz.dot(layer["w"].T)# 更新当前层的权重:使用学习率乘以权重梯度,然后加到原有的权重上(梯度上升)layer["w"] += learning_rate * gw# 更新当前层的偏置:同样使用学习率乘以偏置梯度,然后加到原有的偏置上layer["b"] += learning_rate * gb# 返回传递给前一层的梯度,以便继续进行反向传播return new_dz
二 用 Numpy 来做神经网络
没有训练
def predict(x, l1, l2):o1 = x.dot(l1["w"]) + l1["b"]o2 = o1.dot(l2["w"]) + l2["b"]return [o1, o2]def predict01():# 数据x = np.linspace(-1, 1, 10)[:, None] # shape [10, 1]y = np.random.normal(loc=0, scale=0.2, size=[10, 1]) + x # shape [10, 1]# 搭建模型l1 = layer(1, 3)l2 = layer(3, 1)draw_line(x, predict(x, l1, l2)[-1])draw_scatter(x, y)
运行结果

可以看出在没有训练的时候,模型预测的结果与实际 y 值在数量级上存在较大差异。
开始训练
def predict02():# 数据x = np.linspace(-1, 1, 10)[:, None] # shape [10, 1]y = np.random.normal(loc=0, scale=0.2, size=[10, 1]) + x # shape [10, 1]l1 = layer(1, 3)l2 = layer(3, 1)# 训练 50 次learning_rate = 0.01for i in range(50):# 前向预测o1, o2 = predict(x, l1, l2)# 误差计算if i % 10 == 0:average_cost = np.mean(np.square(o2 - y))print(average_cost)# 反向传播,梯度更新dz2 = -2 * (o2 - y) # 输出误差 (o2 - y)**2 的导数dz1 = backprop(dz2, l2, o1)_ = backprop(dz1, l1, x)# 画一个训练后的图,对比上文中有数值问题的线draw_line(x, predict(x, l1, l2)[-1])draw_scatter(x, y)
运行结果

三 加入激活函数
常用激活函数
# 激活函数
def relu(x):return np.maximum(0, x)def relu_derivative(x): # 导数return np.where(x > 0, np.ones_like(x), np.zeros_like(x))def tanh(x):return np.tanh(x)def tanh_derivative(x): # 导数return 1 - np.square(np.tanh(x))def sigmoid(x):return 1 / (1 + np.exp(-x))def sigmoid_derivative(x): # 导数o = sigmoid(x)return o * (1 - o)非线性计算,不加激活函数
def predict03():# 非线性计算x = np.linspace(-1, 1, 30)[:, None] # shape [30, 1]y = np.random.normal(loc=0, scale=0.2, size=[30, 1]) + x ** 2 # shape [30, 1]# draw_scatter(x, y)# 搭建模型l1 = layer(1, 10)l2 = layer(10, 1)# 训练 300 次learning_rate = 0.01for i in range(300):# 前向预测o1, o2 = predict(x, l1, l2)# 误差计算if i % 10 == 0:average_cost = np.mean(np.square(o2 - y))print(average_cost)# 反向传播,梯度更新dz2 = -2 * (o2 - y) # 输出误差 (o2 - y)**2 的导数dz1 = backprop(dz2, l2, o1)_ = backprop(dz1, l1, x)draw_line(x, predict(x, l1, l2)[-1])draw_scatter(x, y)
运行结果

模型训练结果在量级上出现较大差距,欠拟合。
非线性计算,加入激活函数
def predict04():# 非线性计算x = np.linspace(-1, 1, 30)[:, None] # shape [30, 1]y = np.random.normal(loc=0, scale=0.2, size=[30, 1]) + x ** 2 # shape [30, 1]# 搭建模型l1 = layer(1, 10)l2 = layer(10, 1)# 训练 300 次learning_rate = 0.01for i in range(300):# 前向预测o1, a1, o2 = predictjihuo(x, l1, l2)# 误差计算if i % 10 == 0:average_cost = np.mean(np.square(o2 - y))print(average_cost)# 反向传播,梯度更新dz2 = -2 * (o2 - y) # 输出误差 (o2 - y)**2 的导数dz1 = backprop(dz2, l2, a1)dz1 *= relu_derivative(o1) # 这里要添加对应激活函数的反向传播_ = backprop(dz1, l1, x)draw_line(x, predictjihuo(x, l1, l2)[-1])draw_scatter(x, y)
运行结果

模型成功拟合了这些异常数据点,说明非线性激活函数确实非常有效。
四 完整代码示例
# This is a sample Python script.
from matplotlib import pyplot as plt
import numpy as np# Press ⌃R to execute it or replace it with your code.
# Press Double ⇧ to search everywhere for classes, files, tool windows, actions, and settings.
def draw_scatter(x, y):# 使用 matplotlib 的 scatter 方法来绘制散点图# x.ravel() 和 y.ravel() 将 x 和 y 的二维数组转换为一维数组,适合作为散点图的输入plt.scatter(x.ravel(), y.ravel())# 显示图表plt.show()def draw_line(x, y):idx = np.argsort(x.ravel())plt.plot(x.ravel()[idx], y.ravel()[idx])# plt.show()def layer(in_dim, out_dim):weights = np.random.normal(loc=0, scale=0.1, size=[in_dim, out_dim])bias = np.full([1, out_dim], 0.1)return {"w": weights, "b": bias}# 激活函数
def relu(x):return np.maximum(0, x)def relu_derivative(x): # 导数return np.where(x > 0, np.ones_like(x), np.zeros_like(x))def tanh(x):return np.tanh(x)def tanh_derivative(x): # 导数return 1 - np.square(np.tanh(x))def sigmoid(x):return 1 / (1 + np.exp(-x))def sigmoid_derivative(x): # 导数o = sigmoid(x)return o * (1 - o)def backprop(dz, layer, layer_in, learning_rate=0.01):"""进行反向传播,更新当前层的权重和偏置,并计算传递给前一层的梯度。参数:dz: 当前层输出的梯度(损失函数对激活输出的偏导数)layer: 当前层的参数字典,包含权重 "w" 和偏置 "b"layer_in: 输入到当前层的激活值learning_rate: 学习率,用于控制参数更新的步长,默认值为 0.01返回:new_dz: 传递给前一层的梯度"""# 计算损失函数对权重的梯度,layer_in.T 是当前层输入的转置,dot(dz) 进行矩阵乘法gw = layer_in.T.dot(dz)# 计算损失函数对偏置的梯度,按列求和,保留维度,求得每个偏置的梯度gb = np.sum(dz, axis=0, keepdims=True)# 计算传递给前一层的梯度,使用当前层的权重转置与 dz 相乘new_dz = dz.dot(layer["w"].T)# 更新当前层的权重:使用学习率乘以权重梯度,然后加到原有的权重上(梯度上升)layer["w"] += learning_rate * gw# 更新当前层的偏置:同样使用学习率乘以偏置梯度,然后加到原有的偏置上layer["b"] += learning_rate * gb# 返回传递给前一层的梯度,以便继续进行反向传播return new_dzdef predictjihuo(x, l1, l2):o1 = x.dot(l1["w"]) + l1["b"]a1 = relu(o1) # 这里我添加了一个激活函数o2 = a1.dot(l2["w"]) + l2["b"]return [o1, a1, o2]def predict(x, l1, l2):"""预测函数,执行前向传播,计算两层神经网络的输出。参数:x: 输入数据,形状为 [N, 输入特征数],此处为 [10, 1]。l1: 第一层的参数字典,包含权重 "w" 和偏置 "b"。l2: 第二层的参数字典,包含权重 "w" 和偏置 "b"。返回:o1: 第一层的输出结果。o2: 第二层的输出结果(最终输出)。"""# 第一层的输出,x.dot(l1["w"]) 是线性组合,+ l1["b"] 加上偏置o1 = x.dot(l1["w"]) + l1["b"]# 第二层的输出,o1.dot(l2["w"]) 是线性组合,+ l2["b"] 加上偏置o2 = o1.dot(l2["w"]) + l2["b"]# 返回两层的输出,o1 为第一层的输出,o2 为最终的输出return [o1, o2]def predict01():"""模拟预测和数据绘制函数,包含数据生成、模型搭建、前向预测和绘图。"""# 生成输入数据 x,使用 np.linspace 生成从 -1 到 1 的 10 个均匀分布的点,并reshape为 [10, 1]x = np.linspace(-1, 1, 10)[:, None] # 形状 [10, 1]# 生成目标值 y,基于 x 加上高斯噪声,模拟真实数据,形状为 [10, 1]y = np.random.normal(loc=0, scale=0.2, size=[10, 1]) + x # 形状 [10, 1]# 搭建神经网络模型# 第一层:输入维度为 1,输出维度为 3(即3个神经元)l1 = layer(1, 3)# 第二层:输入维度为 3,输出维度为 1l2 = layer(3, 1)# 使用 predict 函数进行前向传播,绘制预测结果# 只提取第二层的输出 o2 来绘制预测的线draw_line(x, predict(x, l1, l2)[-1])# 绘制真实数据点的散点图draw_scatter(x, y)def predict02():# 数据x = np.linspace(-1, 1, 10)[:, None] # shape [10, 1]y = np.random.normal(loc=0, scale=0.2, size=[10, 1]) + x # shape [10, 1]l1 = layer(1, 3)l2 = layer(3, 1)# 训练 50 次learning_rate = 0.01for i in range(50):# 前向预测o1, o2 = predict(x, l1, l2)# 误差计算if i % 10 == 0:average_cost = np.mean(np.square(o2 - y))print(average_cost)# 反向传播,梯度更新dz2 = -2 * (o2 - y) # 输出误差 (o2 - y)**2 的导数dz1 = backprop(dz2, l2, o1)_ = backprop(dz1, l1, x)# 画一个训练后的图,对比上文中有数值问题的线draw_line(x, predict(x, l1, l2)[-1])draw_scatter(x, y)def predict03():# 非线性计算x = np.linspace(-1, 1, 30)[:, None] # shape [30, 1]y = np.random.normal(loc=0, scale=0.2, size=[30, 1]) + x ** 2 # shape [30, 1]# draw_scatter(x, y)# 搭建模型l1 = layer(1, 10)l2 = layer(10, 1)# 训练 300 次learning_rate = 0.01for i in range(300):# 前向预测o1, o2 = predict(x, l1, l2)# 误差计算if i % 10 == 0:average_cost = np.mean(np.square(o2 - y))print(average_cost)# 反向传播,梯度更新dz2 = -2 * (o2 - y) # 输出误差 (o2 - y)**2 的导数dz1 = backprop(dz2, l2, o1)_ = backprop(dz1, l1, x)draw_line(x, predict(x, l1, l2)[-1])draw_scatter(x, y)def predict04():# 非线性计算x = np.linspace(-1, 1, 30)[:, None] # shape [30, 1]y = np.random.normal(loc=0, scale=0.2, size=[30, 1]) + x ** 2 # shape [30, 1]# 搭建模型l1 = layer(1, 10)l2 = layer(10, 1)# 训练 300 次learning_rate = 0.01for i in range(300):# 前向预测o1, a1, o2 = predictjihuo(x, l1, l2)# 误差计算if i % 10 == 0:average_cost = np.mean(np.square(o2 - y))print(average_cost)# 反向传播,梯度更新dz2 = -2 * (o2 - y) # 输出误差 (o2 - y)**2 的导数dz1 = backprop(dz2, l2, a1)dz1 *= relu_derivative(o1) # 这里要添加对应激活函数的反向传播_ = backprop(dz1, l1, x)draw_line(x, predictjihuo(x, l1, l2)[-1])draw_scatter(x, y)def print_hi(name):# Use a breakpoint in the code line below to debug your script.print(f'Hi, {name}') # Press ⌘F8 to toggle the breakpoint.# 模型前向预测# 数据x = np.linspace(-1, 1, 10)[:, None] # shape [10, 1]y = np.random.normal(loc=0, scale=0.2, size=[10, 1]) + x # shape [10, 1]# draw_scatter(x, y)# 模型l1 = layer(1, 3)l2 = layer(3, 1)# 计算o = x.dot(l1["w"]) + l1["b"]print("第一层出来后的 shape:", o.shape)o = o.dot(l2["w"]) + l2["b"]print("第二层出来后的 shape:", o.shape)print("output:", o)# draw_scatter(x, o)# 简单介绍反向传播# predict01()# predict02()# 加入激活函数# 非线性计算,没有激活函数的网络训练,量级上的差距大# predict03()# 非线性计算,加入激活函数predict04()# Press the green button in the gutter to run the script.
if __name__ == '__main__':print_hi('神经网络-自动训练')# See PyCharm help at https://www.jetbrains.com/help/pycharm/复制粘贴并覆盖到你的 main.py 中运行,运行结果如下。
Hi, 神经网络-自动训练
第一层出来后的 shape: (10, 3)
第二层出来后的 shape: (10, 1)
output: [[0.08015376][0.08221984][0.08428592][0.086352 ][0.08841808][0.09048416][0.09255024][0.09461632][0.0966824 ][0.09874848]]
0.2226335913018929
0.18084056623965614
0.17646520657891238
0.16955062165383475
0.15974897747454914
0.14609449775016456
0.12879398035319886
0.11000871768876343
0.09272999949822598
0.07986100731357502
0.07149628207512877
0.06657668787644673
0.06412748050655417
0.06308965708664192
0.06255298788129363
0.06233764319523034
0.06229224784095634
0.062220235356859256
0.06227320308423159
0.06227607241875045
0.06218961938206315
0.062183519685144004
0.06220136162617964
0.062260925337883535
0.06228186644083771
0.062212564435570314
0.06214763225225857
0.062190709318072676
0.06225667345334308
0.06227302776778138
五 源码地址
代码地址:
国内看 Gitee 之 numpy/神经网络-自动训练.py
国外看 GitHub 之 numpy/神经网络-自动训练.py
引用 莫烦 Python
相关文章:

Python Numpy 实现神经网络自动训练:反向传播与激活函数的应用详解
Python Numpy 实现神经网络自动训练:反向传播与激活函数的应用详解 这篇文章介绍了如何使用 Python 的 Numpy 库来实现神经网络的自动训练,重点展示了反向传播算法和激活函数的应用。反向传播是神经网络训练的核心,能够通过计算梯度来优化模…...

Apache Calcite - 基于规则的查询优化
基于规则的查询优化 基于规则的查询优化(Rule-based Query Optimization)是一种通过应用一系列预定义的规则来优化查询计划的技术。这些规则描述了如何转换关系表达式,以提高查询执行的效率。基于规则的优化器并不依赖于统计信息,…...

react学习笔记,ReactDOM,react-router-dom
react 学习 1. 下载与安装 下载 npm install -g create-react-app 安装 npx create-react-app xxx 推荐 npm init react-app xxx yarn create react-app xxx 2. 创建 react 元素 indexjs 文件 import React from "react"; import ReactDOM from "react…...

优化UVM环境(八)-整理project_common_pkg文件
书接上回: 优化UVM环境(七)-整理环境,把scoreboard拿出来放在project_common环境里 Prj_cmn_pkg.sv考虑到是后续所有文件的基础,需要引入uvm_pkg并把自身这个pkg import给后续的文件: 这里有3个注意事项&…...

【实战案例】Django框架连接并操作数据库MySQL相关API
本文相关操作基于上次操作基本请求及响应基础之上【实战案例】Django框架基础之上编写第一个Django应用之基本请求和响应 Django框架中默认会连接SQLite数据库,好处是方便无需远程连接,打包项目挪到其他环境安装一下依赖一会就跑起来,但是缺点…...

【其他】无法启动phptudy服务,提示错误2:系统找不到指定的文件
在服务中启动phpstudy服务时,提示“windows 无法启动phpstudy服务 服务(位于本地计算机上) 错误2:系统找不到指定的文件”的错误。导致错误的原因是可执行文件的路径不对,修改成正确的路径就可以了。 下面是错误的路径,会弹出错误窗口&#…...

AI驱动的支持截图或线框图快速生成网页应用的开源项目
Napkins.dev是什么 Napkins.dev是一个创新的开源项目,基于AI技术将用户的截图或线框图快速转换成可运行的网页应用程序。项目背后依托于Meta的Llama 3.1 405B大型语言模型和Llama 3.2 Vision视觉模型,结合Together.ai的推理服务,实现从视觉设…...

es集群索引是黄色
排查 GET /_cat/shards?hindex,shard,prirep,state,unassigned.reason 查询原因 发现node正常 执行重新分配 retry_failedtrue 参数告诉Elasticsearch重试那些因某种原因(如节点故障、资源不足等)而失败的分片分配。这个选项通常用来尝试再次分配那些…...

获取淘宝商品评论的方法分享-调用API接口item_review
在电商领域,商品评论是消费者了解产品、做出购买决策的重要依据。淘宝作为中国最大的电商平台之一,其商品评论系统涵盖了海量的用户反馈数据。为了帮助企业、电商数据分析师、市场研究人员以及普通消费者更高效地获取这些评论数据,淘宝开放平…...

MATLAB人脸考勤系统
MATLAB人脸考勤系统课题介绍 该课题为基于MATLAB平台的人脸识别系统。传统的人脸识别都是直接人头的比对,现实意义不大,没有一定的新意。该课题识别原理为:先采集待识别人员的人脸,进行训练,得到人脸特征值。测试的时…...
Spring篇(事务篇 - 基础介绍)
目录 一、JdbcTemplate(持久化技术) 1. 简介 2. 准备工作 2.1. 引入依赖坐标 2.2. 创建jdbc.properties 2.3. 配置Spring的配置文件 3. 测试 3.1. 在测试类装配 JdbcTemplate 3.2. 测试增删改功能 查询一条数据为实体类对象 查询多条数据为一个…...

qt EventFilter用途详解
一、概述 EventFilter是QObject类的一个事件过滤器,当使用installEventFilter方法为某个对象安装事件过滤器时,该对象的eventFilter函数就会被调用。通过重写eventFilter方法,开发者可以在事件处理过程中进行拦截和处理,实现对事…...

[ 钓鱼实战系列-基础篇-6 ] 一篇文章让你了解邮件服务器机制(SMTP/POP/IMAP)-1
🍬 博主介绍 👨🎓 博主介绍:大家好,我是 _PowerShell ,很高兴认识大家~ ✨主攻领域:【渗透领域】【数据通信】 【通讯安全】 【web安全】【面试分析】 🎉点赞➕评论➕收藏 养成习…...

wordpress伪静态规则
WordPress 伪静态规则是指将 WordPress 生成的动态 URL 转换为静态 URL 的规则,这样做可以提高网站的搜索引擎优化(SEO)效果,并且使得 URL 更加美观、易于记忆。伪静态规则通常需要在服务器的配置文件中设置,不同的服务器环境配置方法有所不同…...
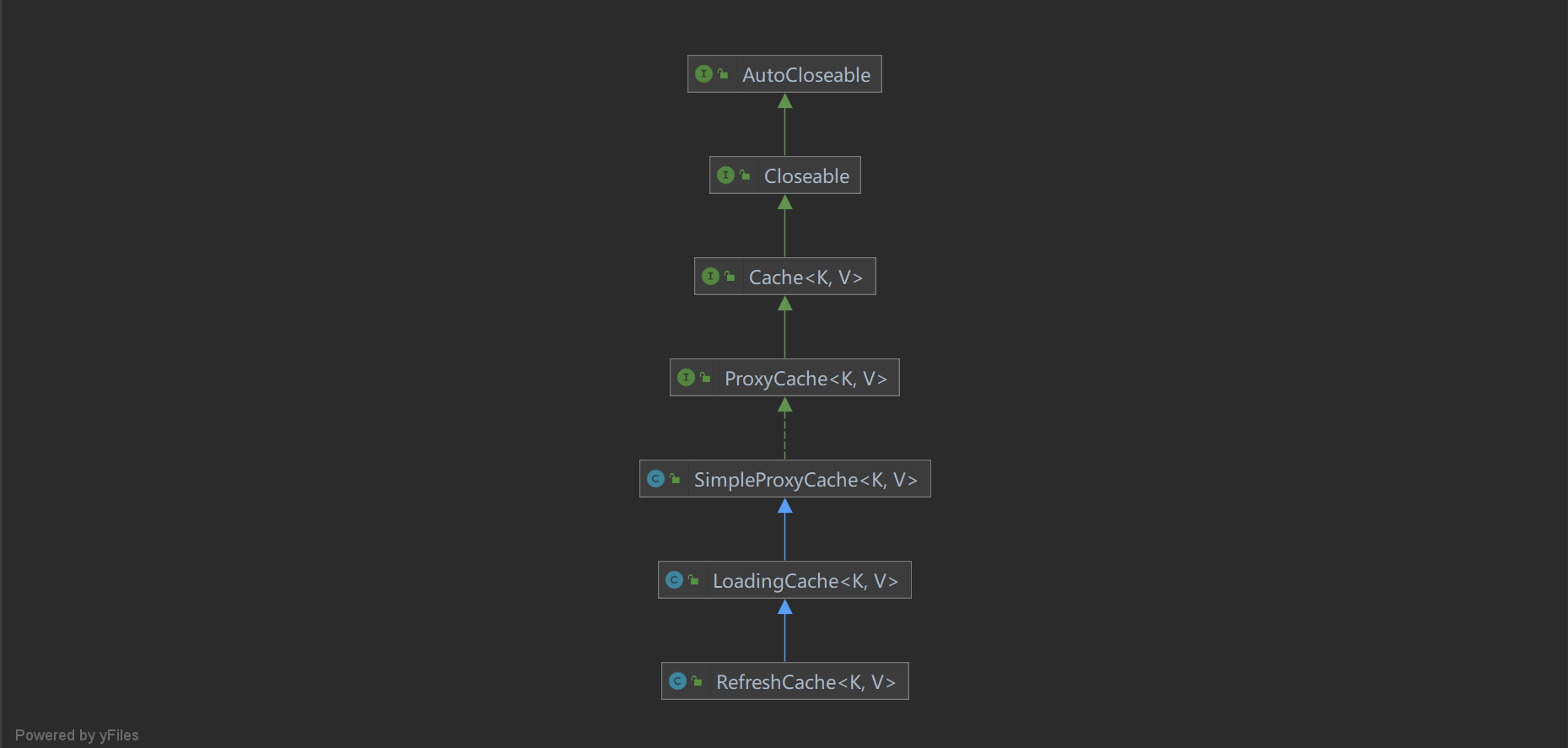
缓存框架JetCache源码解析-缓存定时刷新
作为一个缓存框架,JetCache支持多级缓存,也就是本地缓存和远程缓存,但是不管是使用着两者中的哪一个或者两者都进行使用,缓存的实时性一直都是我们需要考虑的问题,通常我们为了尽可能地保证缓存的实时性,都…...

docker配置mysql8报错 ERROR 2002 (HY000)
通过docker启动的mysql,发现navicat无法连接,后来进入容器内部也是无法连接,产生以下错误 root9f3b90339a14:/var/run/mysqld# mysql -u root -p Enter password: ERROR 2002 (HY000): Cant connect to local MySQL server through socket …...

【Linux】为什么环境变量具有全局性?共享?写时拷贝优化?
环境变量表具有全局性的原因: 环境变量表之所以具有全局性的特征,主要是因为它们是在进程上下文中维护的,并且在大多数操作系统中,当一个进程创建另一个进程(即父进程创建子进程)时,子进程会继承…...

如何在Linux中找到MySQL的安装目录
前言 发布时间:2024-10-22 在日常管理和维护数据库的过程中,了解MySQL的确切安装位置对于执行配置更改、更新或者进行故障排查是非常重要的。本文将向您介绍几种在Linux环境下定位MySQL安装路径的方法。 通过命令行工具快速定位 使用 which 命令 首…...

机器人备件用在哪些领域
机器人备件,作为机器人技术的重要组成部分,被广泛应用于多个领域,以提高生产效率、降低成本、增强产品质量,并推动相关行业的智能化发展。以下是一些主要的应用领域: 制造业: 机器人备件在制造业中的应用最…...

基于单片机优先级的信号状态机设计
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、背景知识二、使用步骤1.定义相应状态和信号列表2.获取最高优先级信号3.通用状态机实现4.灯的控制函数 总结 前言 在嵌入式系统中,设备控制的灵…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...

Python 包管理器 uv 介绍
Python 包管理器 uv 全面介绍 uv 是由 Astral(热门工具 Ruff 的开发者)推出的下一代高性能 Python 包管理器和构建工具,用 Rust 编写。它旨在解决传统工具(如 pip、virtualenv、pip-tools)的性能瓶颈,同时…...

Kafka入门-生产者
生产者 生产者发送流程: 延迟时间为0ms时,也就意味着每当有数据就会直接发送 异步发送API 异步发送和同步发送的不同在于:异步发送不需要等待结果,同步发送必须等待结果才能进行下一步发送。 普通异步发送 首先导入所需的k…...

消息队列系统设计与实践全解析
文章目录 🚀 消息队列系统设计与实践全解析🔍 一、消息队列选型1.1 业务场景匹配矩阵1.2 吞吐量/延迟/可靠性权衡💡 权衡决策框架 1.3 运维复杂度评估🔧 运维成本降低策略 🏗️ 二、典型架构设计2.1 分布式事务最终一致…...

高考志愿填报管理系统---开发介绍
高考志愿填报管理系统是一款专为教育机构、学校和教师设计的学生信息管理和志愿填报辅助平台。系统基于Django框架开发,采用现代化的Web技术,为教育工作者提供高效、安全、便捷的学生管理解决方案。 ## 📋 系统概述 ### 🎯 系统定…...

React从基础入门到高级实战:React 实战项目 - 项目五:微前端与模块化架构
React 实战项目:微前端与模块化架构 欢迎来到 React 开发教程专栏 的第 30 篇!在前 29 篇文章中,我们从 React 的基础概念逐步深入到高级技巧,涵盖了组件设计、状态管理、路由配置、性能优化和企业级应用等核心内容。这一次&…...
