【leetcode|哈希表、动态规划】最长连续序列、最大子数组和
目录
最长连续序列
解法一:暴力枚举
复杂度
解法二:优化解法一省去二层循环中不必要的遍历
复杂度
最大子数组和
解法一:暴力枚举
复杂度
解法二:贪心
复杂度
解法三:动态规划
复杂度
最长连续序列

输入输出示例:

解法一:暴力枚举
两层循环,第一层循环是遍历整个数组;第二层循环的目的是得到最长连续序列时间复杂度极高,效率低下。
1、如果不使用哈希表在枚举过程中查找nums[i]+1时要通过遍历整个数组来进行,因此时间复杂度是O(n^2)
2、使用哈希表枚在举过程中虽说哈希表查找数据的时间复杂度是O(1),但第二次循环仍然需要执行多次,最坏的情况下其时间复杂度也会接近O(n^2)
class Solution {
public:int longestConsecutive(vector<int>& nums) {if(0 == nums.size()) //注意:需要考虑nums为空的情况,此时的最长连续序列就是0return 0;unordered_set<int> hashtable;int max_length = INT_MIN;for(const auto& e:nums) //使用哈希表去重数据hashtable.emplace(e);for(const auto& e:hashtable){int tmp = e;int cnt = 1;while(hashtable.count(++tmp))++cnt;max_length = std::max(max_length,cnt);}return max_length;}
};
复杂度
时间复杂度: O(n^2)
空间复杂度:O(n)
解法二:优化解法一省去二层循环中不必要的遍历
class Solution {
public:int longestConsecutive(vector<int>& nums) {if(0 == nums.size())return 0;int size = nums.size();int max_length = 0;unordered_set<int> hashtable;for(const auto& e:nums)hashtable.insert(e);for(const auto& e:hashtable){if(!hashtable.count(e-1))//只在哈希表中找连续序列的第一个数{int cnt = 1;int tmp = e;while(hashtable.count(++tmp))++cnt;max_length = std::max(max_length,cnt);}}return max_length;}
};
复杂度
时间复杂度:O(n)
空间复杂度:O(n)
最大子数组和

输入输出示例

解法一:暴力枚举
两层循环,定义一个max_sum变量,第二层循环中定义一个tmp变量用来记录第二层循环中连续子数组的和。
lass Solution {
public:int maxSubArray(vector<int>& nums) {int size = nums.size();int max_sum = INT_MIN;for(int i = 0;i<size;++i){int tmp = 0; //用来记录连续子数组的和for(int j = i;j<size;++j){tmp += nums[j];max_sum = std::max(max_sum,tmp);}}return max_sum;}
};该暴力枚举会超出时间限制,不适合。
复杂度
时间复杂度:O(n^2)
空间复杂度:O(1)
解法二:贪心
class Solution {
public:int maxSubArray(vector<int>& nums) {int size = nums.size();int max_sum = nums[0]; //考虑到数组nums只有一个元素的时候,加上题目限制:子数组中至少包含一个元素int tmp = nums[0];for(int i = 1;i<size;++i){if(tmp > 0)tmp += nums[i];elsetmp = nums[i];max_sum = std::max(max_sum,tmp);}return max_sum;}
};复杂度
时间复杂度:O(n)
空间复杂度:O(1)
解法三:动态规划
定义一个dp数组,dp[i]表示以 i 位置结尾的子数组的最大和,利用已经有的dp[i-1]值求dp[i]。

class Solution {
public:int maxSubArray(vector<int>& nums) {int size = nums.size();vector<int> dp(size);//dp[i]表示以i位置结尾的连续子数组的最大和dp[0] = nums[0];int max_sum = dp[0];//当size == 1的时候程序不进入下面循环,直接返回nums[0]for(int i = 1;i<size;++i){if(dp[i-1]>0)dp[i] = dp[i-1] + nums[i];elsedp[i] = nums[i];max_sum = std::max(max_sum,dp[i]);}return max_sum;}
};复杂度
时间复杂度:O(n)
空间复杂度:O(n)
使用滚动数组将空间复杂度优化为O(1):
class Solution {
public:int maxSubArray(vector<int>& nums) {int size = nums.size();//vector<int> dp(size);//dp[i]表示以i位置结尾的连续子数组的最大和int dp1 = nums[0];int dp2 = 0;int max_sum = dp1;for(int i = 1;i<size;++i){if((dp1+nums[i]) > nums[i])dp2 = dp1 + nums[i];elsedp2 = nums[i];max_sum = std::max(max_sum,dp2);dp1 = dp2;//更新dp1}return max_sum;}
};相关文章:

【leetcode|哈希表、动态规划】最长连续序列、最大子数组和
目录 最长连续序列 解法一:暴力枚举 复杂度 解法二:优化解法一省去二层循环中不必要的遍历 复杂度 最大子数组和 解法一:暴力枚举 复杂度 解法二:贪心 复杂度 解法三:动态规划 复杂度 最长连续序列 输入输…...

【人工智能】掌握深度学习中的时间序列预测:深入解析RNN与LSTM的工作原理与应用
深度学习中的循环神经网络(RNN)和长短时记忆网络(LSTM)在处理时间序列数据方面具有重要作用。它们能够通过记忆前序信息,捕捉序列数据中的长期依赖性,广泛应用于金融市场预测、自然语言处理、语音识别等领域…...

今日开放!24下软考机考「模拟练习平台」操作指南来啦!
2024年下半年软考机考模拟练习平台今日开放,考生可以下载模拟作答系统并登录后进行模拟练习,熟悉答题流程及操作方法。 一、模拟练习时间 2024年下半年软考机考模拟练习平台开放时间为2024年10月23日9:00至11月6日17:00,共15天。 考生可以在…...

合并.md文档
需求:将多个.md文档合并成一个.md文档。 方法一:通过 type 命令 参考内容:多个md文件合并 步骤: 把需要合并的 .md 文档放入到一个文件夹内。修改需要合并的 .md 文档名,可以在文档名前加上 1.2.3 来表明顺序&#x…...

10月18日笔记(基于系统服务的权限提升)
系统内核漏洞提权 当目标系统存在该漏洞且没有更新安全补丁时,利用已知的系统内核漏洞进行提权,测试人员往往可以获得系统级别的访问权限。 查找系统潜在漏洞 手动寻找可用漏洞 在目标主机上执行以下命令,查看已安装的系统补丁。 system…...

【STM32 Blue Pill编程实例】-控制步进电机(ULN2003+28BYJ-48)
控制步进电机(ULN2003+28BYJ-48) 文章目录 控制步进电机(ULN2003+28BYJ-48)1、步进电机介绍2、ULN2003步进电机驱动模块3、硬件准备及接线4、模块配置3.1 定时器配置3.2 ULN2003输入引脚配置4、代码实现在本文中,我们将介使用 STM32Cube IDE 使用 ULN2003 电机驱动器来控制28B…...

监督学习、无监督学习、半监督学习、强化学习、迁移学习、集成学习分别是什么对应什么应用场景
将对监督学习、无监督学习、半监督学习、强化学习、迁移学习和集成学习进行全面而详细的解释,包括定义、应用场景以及具体的算法/模型示例。 1. 监督学习 (Supervised Learning) 定义:监督学习是一种机器学习方法,其中模型通过已知的输入数…...

WSL2 Linux子系统调整存储位置
WSL2 默认不支持修改Linux 安装路径,官方提供的方式,只有通过导出、导入的方式实现Linux子系统的迁移。 修改注册表的方式官方不推荐,没有尝试过,仅提供操作方式(自行评估风险,建议备份好数据) 1. 打开 **注册表编辑器…...

Shiro授权
一、定义与作用 授权(Authorization),也称为访问控制,是确定是否允许用户/主体做某事的过程。在Shiro安全框架中,授权是核心组件之一,它负责控制用户对系统资源的访问权限,确保用户只能访问其被…...
算法题总结(十五)——贪心算法(下)
1005、K 次取反后最大化的数组和 给你一个整数数组 nums 和一个整数 k ,按以下方法修改该数组: 选择某个下标 i 并将 nums[i] 替换为 -nums[i] 。 重复这个过程恰好 k 次。可以多次选择同一个下标 i 。 以这种方式修改数组后,返回数组 可…...

《深度学习》【项目】自然语言处理——情感分析 <下>
目录 一、了解项目 1、任务 2、文件内容 二、续接上篇内容 1、打包数据,转化Tensor类型 2、定义模型,前向传播函数 3、定义训练、测试函数 4、最终文件格式 5、定义主函数 运行结果: 一、了解项目 1、任务 对微博评论信息的情感分…...

postgresql是国产数据库吗?
PostgreSQL不是国产数据库。但是PostgreSQL对国产数据库的发展有着重要影响,许多国产数据库产品是基于PostgreSQL进行二次开发的。 PostgreSQL的开源特性也是其受欢迎的重要原因之一。开源意味着任何人都可以查看、修改和使用PostgreSQL的源代码。这使得PostgreSQL…...
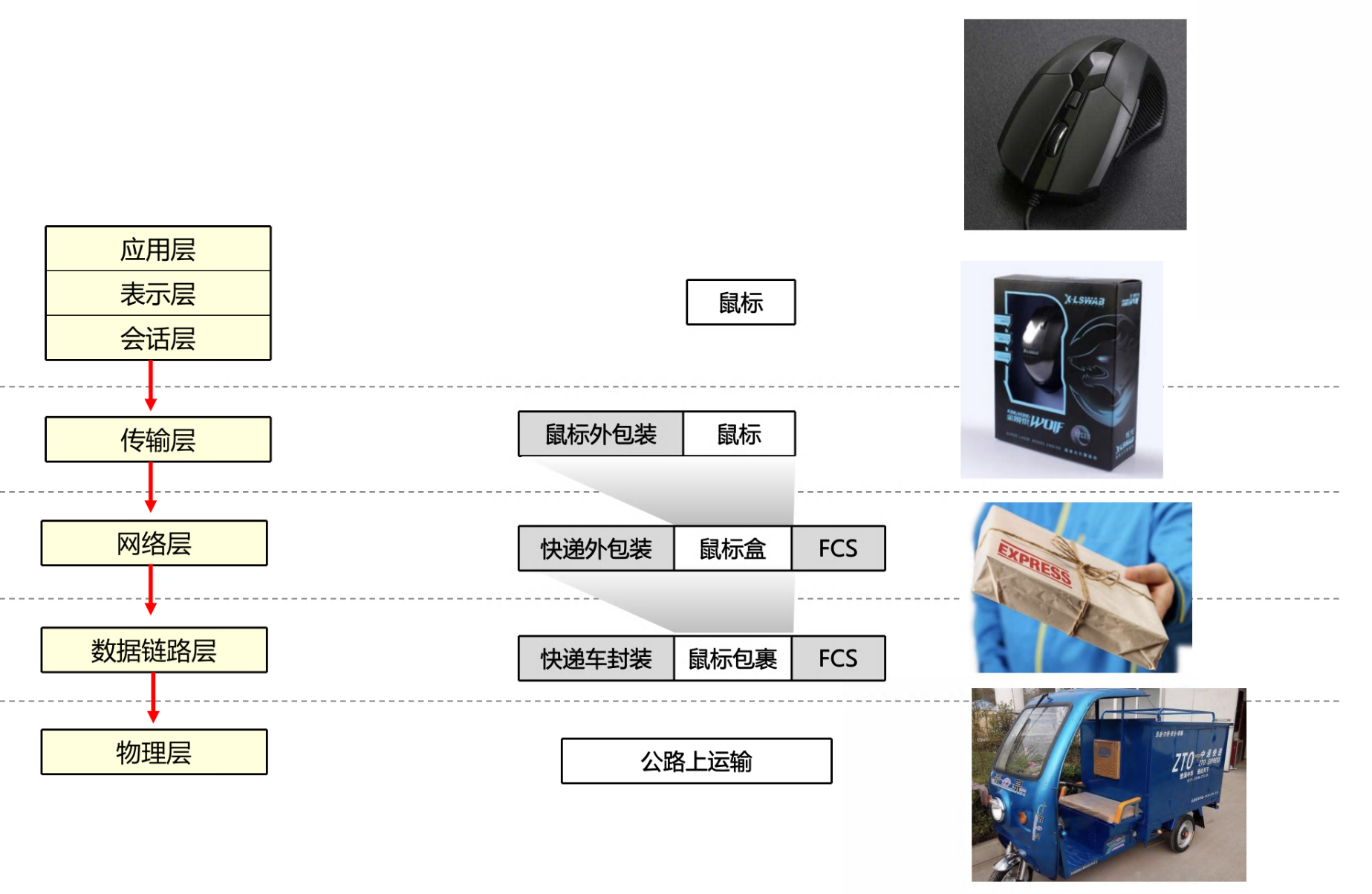
软考——计算机网络概论
文章目录 🕐计算机网络分类1️⃣通信子网和资源子网2️⃣网络拓扑结构3️⃣ 计算机网络分类3:LAN MAN WAN4️⃣其他分类方式 🕑OSI 和 TCP/IP 参考模型1️⃣OSI2️⃣TCP/IP🔴TCP/IP 参考模型对应协议 3️⃣OSI 和 TCP/IP 模型对应…...

01 设计模式-创造型模式-工厂模式
工厂模式(Factory Pattern)是 Java 中最常用的设计模式之一,它提供了一种创建对象的方式,使得创建对象的过程与使用对象的过程分离。 工厂模式提供了一种创建对象的方式,而无需指定要创建的具体类。 通过使用工厂模式…...

ComnandLineRunner接口, ApplcationRunner接口
ComnandLineRunner接口, ApplcationRunner接口 介绍: 这两个接口都有一个run方法,执行时间在容器对象创建好后,自动执行run ( )方法。 创建容器的同时会创建容器中的对象,同时会把容器中的对象的属性赋上值: 举例&…...

Swift用于将String拆分为数组的components与split的区别
根据特定分隔符拆分字符串 在 Swift 中,components(separatedBy:) 和 split(separator:) 都可以用于将字符串拆分为数组,但它们有一些关键区别。下面将从返回值类型、性能和功能等角度进行对比。 1. 返回值类型 components(separatedBy:):…...
)
docker之redis安装(项目部署准备)
创建网络 docker network create net-ry --subnet172.68.0.0/16 --gateway172.68.0.1 redis安装 #创建目录 mkdir -p /data/redis/{conf,data} #上传redis.conf文件到/data/redis/conf文件夹中 #对redis.conf文件修改 # bind 0.0.0.0 充许任何主机访问 # daemonize no #密码 # …...

使用Maven前的简单准备
目录 一、Maven的准备 1、安装jdk1.8或以上版本 2、下载Maven 3、安装Maven 二、Maven目录的分析 三、Maven的环境变量配置 1、设置MAVEN_HOME环境变量 2、设置Path环境变量 3、验证配置是否完成 一、Maven的准备 1、安装jdk1.8或以上版本 jdk的安装 2、下载Maven…...

Java | Leetcode Java题解之第494题目标和
题目: 题解: class Solution {public int findTargetSumWays(int[] nums, int target) {int sum 0;for (int num : nums) {sum num;}int diff sum - target;if (diff < 0 || diff % 2 ! 0) {return 0;}int neg diff / 2;int[] dp new int[neg …...

阅读笔记 Contemporary strategy analysis Chapter 13
来源:Robert M. Grant - Contemporary strategy analysis (2018) Chapter 13 Implementing Corporate Strategy: Managing the Multibusiness Firm Ⅰ Introduction and Objectives 多业务公司 multibusiness firm由多个独立的业务部门组成,如业务单元…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...
