九龙证券|“春季躁动”行情要来?1月新增投资者数大增
新增投资者数量在上一年12月触及多年新低后,2023年1月份开端呈现反弹。
在新增投资者数量之外,近段时刻以来,包含A股商场股票成交额、北向资金净买入额、两融资金规划及成交额在内多个商场目标也呈现回暖的特征,目前A股商场交投氛围和投资者决心已较上一年低位有显着修复。
新增投资者数反弹,1月新增投资者数达84.48万
根据我国结算发表的数据,2023年1月,新增投资者数达84.48万,期末投资者数达21,298.10万(即2.1298亿)。
值得注意的是,这意味着,在2022年12月新增投资者数触及多年新低后,月度新增投资者数开端呈现反弹。
数据显现,此前的2022年12月,新增投资者数仅为71.24万,创下2015年4月该项数据开端发布以来的新低。
一般以为,新增投资者数与商场走势、投资者决心等有必定关系。本年1月份新增投资者数量企稳反弹,必定程度上意味着商场决心已显着回暖。考虑到本年1月份还存在春节长假休市使得交易天数较少的因素,1月份投资者决心修复程度实践还要更大一些。
不过,1月份新增投资者数量离近年的月度平均水平仍有必定距离。
据记者计算,2015年4月至2023年1月间,月度新增投资者平均数约为145万户。2015年的A股商场大牛市期间的不少月份,月度新增投资者数量一度在400万以上。
商场决心显着回暖
新增投资者数量触底反弹,仅仅最近一个多月来以来商场决心回暖的一个缩影。
实践上,除了新增投资者数量外,多个商场目标也呈现回暖的特征。
商场交投方面,近一段时期以来,A股商场股票日成交额已回到9000亿元上下的水平,不少交易日已突破1万亿元,这一成交水平较2022年12月下旬的成交水平有显着提升,其时A股商场股票日成交额一度跌破6000亿元。
作为本年以来加仓A股最为坚决的力量之一,北向资金对A股商场的介入力度的增强更是显着。数据显现,2023年初至2月10日,北向资金累计净买入额已高达1496亿元,其间的2023年1月4日至2月2日,北向资金接连17个交易日净买入。近几个交易日,随着美元指数阶段性走强,北向资金意向虽有所反复,但整体也未呈现大幅净卖出趋势。
两融资金方面,从2023年1月30日至2月9日,融资融券余额实现9连增,虽然这期间A股商场已呈现较大震动和调整。近期两融资金的交投规划也有必定增加,上述9个交易日期间,两融日成交金额均超过了600亿元,大都交易日都超过了700亿元。相较之下,2022年12月,两融日成交金额一度跌破400亿元。
对于目前的商场,信达证券近日的研究报告以为,季度装备方面,消费、金融、生长可能有轮番体现的时机。考虑到一季度的季节性,月度装备中能够适当重视生长补涨。金融股在熊市末段到牛市初段持有,挨近经济上升期减仓。该组织以为,目前仍在经济上升期左侧阶段,金融股还能够继续持有。消费股因为曩昔2年存在超跌,曩昔1个季度估值修复的速度很快。信达证券以为这一次消费股的上涨主要获益于经济Beta带来的超跌修复,能够持有到经济上升初期(房地产销售数据改善前)。周期股装备时刻则可能需更挨近经济上升期,现阶段能够重视一些超跌的地产链上游周期板块的提早体现。
华福证券近日的策略观点指出,整体看,A股春季烦躁呈现概率较高,近十年来仅2014、2022年未呈现显着春季烦躁(2015年上半年整体为牛市);春季烦躁持续时刻超过一个月,从开端时刻上来看,随着越来越多的投资者开端熟悉并提早布局,“春季烦躁”有在元旦前后发动的规律,从而使春季烦躁慢慢变成“跨年烦躁”;从完毕时刻来看,春季烦躁大概率在3月两会及4月政治局会议之间终结。该组织以为,预期本年春季烦躁期间,价值领先,生长跟上。且很大概率在消费和金融中轮动切换。在当前经济整体开端显著修复,价值打出“先头炮”,很可能是消费和大金融前期领涨。而春节后,生长股开端跟上,能够重视方位较低的军工、半导体、信创等板块,预计整体商场都将体现不俗。
相关文章:

九龙证券|“春季躁动”行情要来?1月新增投资者数大增
新增投资者数量在上一年12月触及多年新低后,2023年1月份开端呈现反弹。 在新增投资者数量之外,近段时刻以来,包含A股商场股票成交额、北向资金净买入额、两融资金规划及成交额在内多个商场目标也呈现回暖的特征,目前A股商场交投氛…...

C语言(按位运算符和位移运算符)
目录 编辑 一.按位运算符 1.二进制反码或按位取反:~ 2.按位与:& 3.按位或:| 4.按位异或:^ 二.位移运算符 1.左移: << 2.右移: >> 一.按位运算符 C有四个按位逻辑运算符都用于整…...

删掉的照片怎么恢复?
每一张照片都是生活,留住每一个人的回忆。而这些有意义的照片,我们都会把它保存在我们的手机或电脑上,始终伴随着我们。但无论是手机还是电脑,都是需要时不时清理一下的。如果是清理垃圾图片时,不小心删除了需要的图片…...
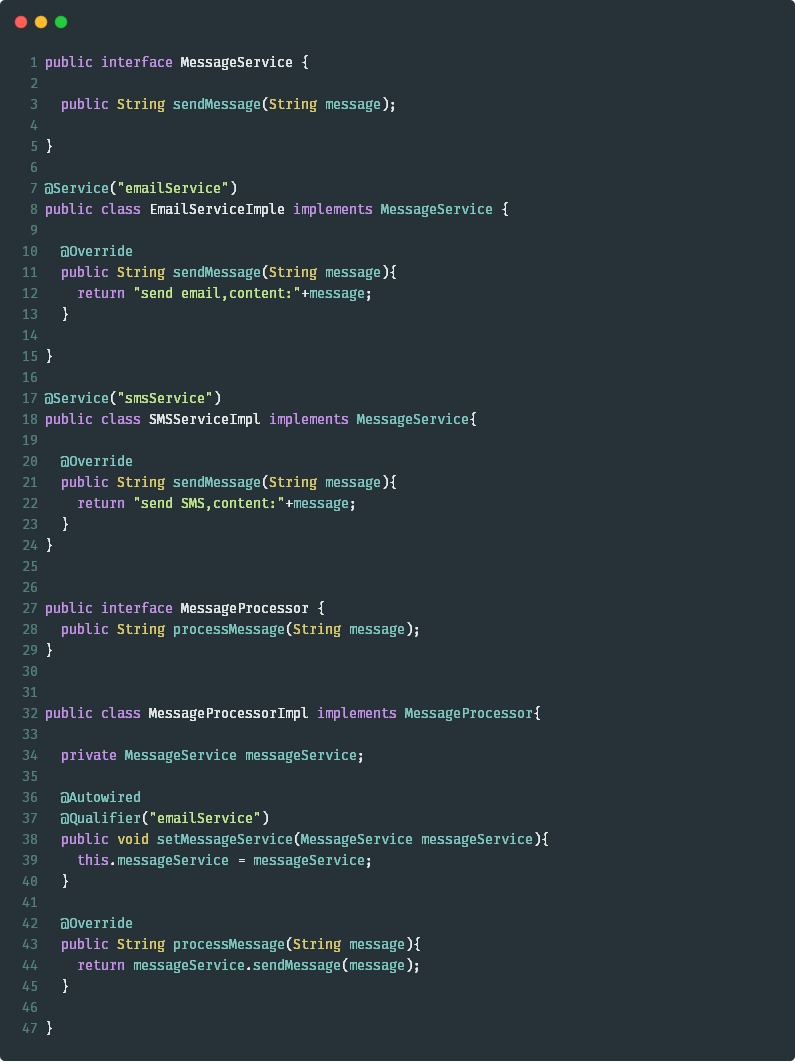
【java】40 个 SpringBoot 常用注解(建议收藏)
本文目录一、Spring Web MVC 注解Spring Web MVC 注解RequestMappingRequestBodyGetMappingPostMappingPutMappingDeleteMappingPatchMappingControllerAdviceResponseBodyExceptionHandlerResponseStatusPathVariableRequestParamControllerRestControllerModelAttributeCross…...

【JMC】SMILES‑based deep generative scafold decorator for de‑novo drug design
SMILES-based deep generative scaffold decorator for de-novo drug design 基于SMILES的利用Fragment的分子生成模型 https://github.com/undeadpixel/reinvent-scaffold-decorator 1.背景 深度生成模型因其可以从有限的数量中生成新数据,目前已成功应用于生成…...

全链路异步,让你的 SpringCloud 性能优化10倍+
背景 随着业务的发展,微服务应用的流量越来越大,使用到的资源也越来越多。 在微服务架构下,大量的应用都是 SpringCloud 分布式架构,这种架构,总体是全链路同步模式。 同步编程模式不仅造成了资源的极大浪费&#x…...

131.《router v 5 与 react-router v 6》
文章目录1.什么是路由2.路由分类3.react-router-dom的理解4. react-router-dom相关API5.其他6. react-router5 路由基本使用1.效果2.代码App.js一级路由home.js下的二级路由7.路由传参的三种方式8.react-router6 基本使用1.一级路由2.二级路由3.hooksuseRoutesuseParamsuseSear…...

2023第十届北京老年产业博览会/中国养老护理人才培育计划
CBIAIE北京老博会,打造2023年度唯具参展价值的老年行业盛会; 北京老博会:2011年,我国首场以“老年产业”为主题,一场专注于老年福祉、健康的国际型行业发展盛会,中国(北京)国际老年…...
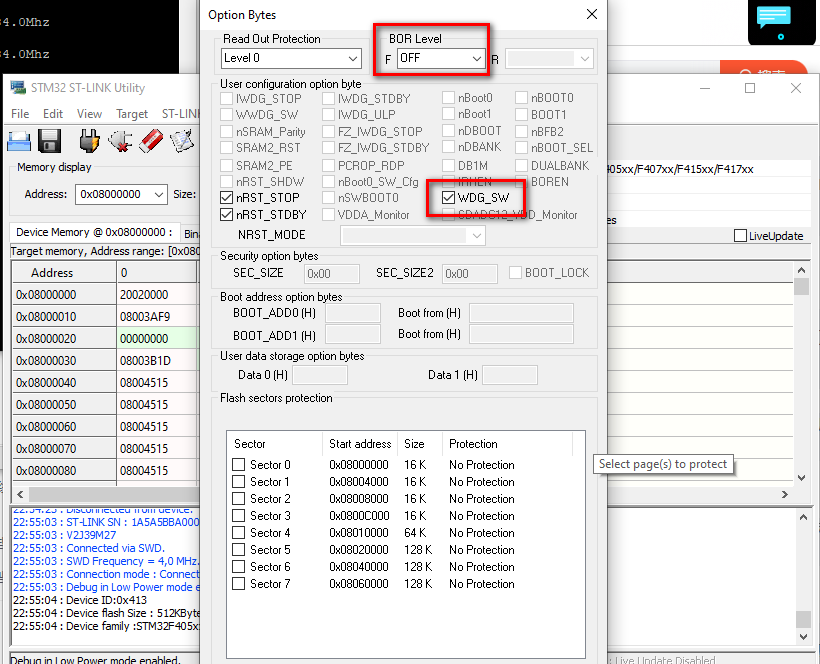
STM32F407VET6 / BLACK_F407VE开发板间隔0.5秒不断重启
有一块 STM32F407VET6 的故障开发板, 之前的问题是经常无法烧录, 必须reset之后才能连接, 具体查看这篇 STM32F407VET6烧录出现flash download failed target dll has been cancelled. 并且程序运行一段时间后会halt. 这块开发板后来一直搁箱底吃灰了几年. 最近打算把这片 STM…...

什么是圈复杂度
圈复杂度是一种软件度量指标,用于度量程序中的控制流程的复杂性。它是通过计算程序中独立路径的数量来确定的。简单来说,圈复杂度是指在一个函数或模块中有多少个独立的路径,也就是说,有多少个不同的输入序列可以导致不同的执行路…...

Hbase 数据迁移
Hbase 数据迁移 可选方案对比 l 已验证方案操作说明: n Export&import u 导出命令及示例 hbase org.apache.hadoop.hbase.mapreduce.Export “表名” 文件路径 导出至本地文件系统: ./bin/hbase org.apache.hadoop.hbase.mapreduce.Export ‘defa…...

Docker consul的容器服务更新与发现
一、Consul概述(1)什么是服务注册与发现服务注册与发现是微服务架构中不可或缺的重要组件。起初服务都是单节点的,不保障高可用性,也不考虑服务的压力承载,服务之间调用单纯的通过接口访问。直到后来出现了多个节点的分…...

数据库关系模型
关系模型简述 形象地说,一个关系就是一个table。 关系模型就是处理table的,它由三个部分组成: 描述DB各种数据的基本结构形式;描述table与table之间所可能发生的各种操作;描述这些操作所应遵循的约束条件࿱…...
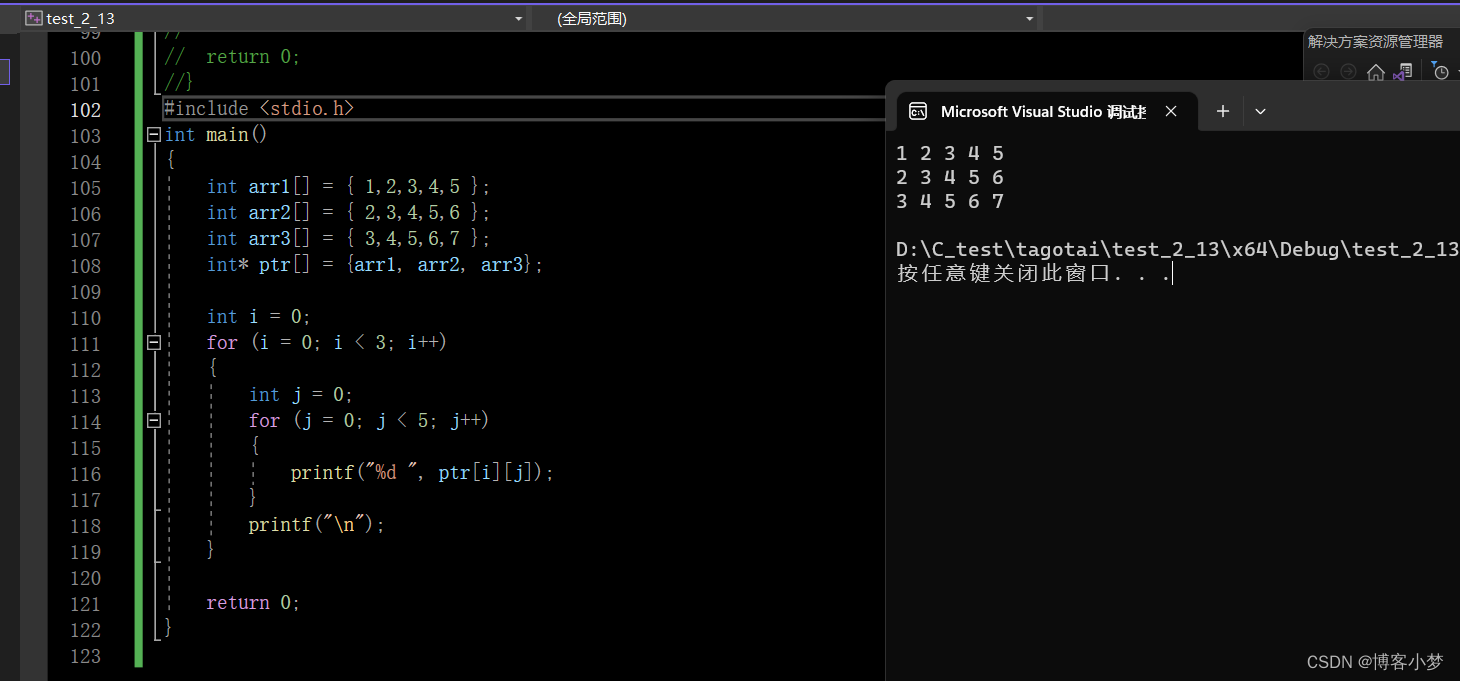
你是真的“C”——详解指针知识
你是真的“C”——详解指针知识😎前言🙌1、 指针是什么?🙌2、指针和指针类型🙌2 、1指针-整数2 、 2指针的解引用3、 野指针🙌3、 1野指针成因3、 2如何规避野指针4、指针运算🙌4、1 指针-整数4…...
)
React/ReactNative面试攻略(偏RN)
useMemo Vs useCallBackuseMemo第一个参数返回的是值,useCallBack返回的是函数useMemo和useCallBack第二个参数都是依赖项useMemo避免组件非依赖项更新时参数的计算useCallback避免父组件非依赖项更新时造成子组件的重复渲染React.memo 使用场景纯prue组件ÿ…...
Leetcode-每日一题1234. 替换子串得到平衡字符串(滑动窗口 + 哈希表)
题目链接:https://leetcode.cn/problems/replace-the-substring-for-balanced-string/description/ 思路 题目意思 这题意思是一个只含有[Q, W, E, R] 四个字符的字符串s且长度一定是 4的倍数, 需要你通过替换子串,使他变成一个「平衡字符…...

linux命令小结-查看日志命令
一、查看日志命令cat查看文件 vi编辑后可以用cat进行查看保存是否成功1)cat -n alert_monitor.log2)cat -n alert_monitor.log | tail -n 100 | head -n 20 //查询100行之后的日志,且在100行之后里再查前20条日志more 可以通过回撤键翻页mor…...

Java知识点细节简易汇总——(8)枚举和注解+Java面向对象高级作业
一、枚举 自定义枚举 当我们使用 enum 关键字开发一个枚举类时,默认会继承 Enum 类, 而且是一个 final 类[如何证明],老师使用 javap 工具来演示传统的 public static final Season2 SPRING new Season2(“春天”, “温暖”); 简化成 SPRING(“春天”, “温暖”)…...

快速上手JVM- Java Virtual Machine面试不用慌
一、JVM的定义 JVM是Java Virtual Machine(Java虚拟机)的缩写,JVM是一种用于计算设备的规范,它是一个虚构出来的计算机,是通过在实际的计算机上仿真模拟各种计算机功能来实现的。 引入Java语言虚拟机后,J…...

安警官的IP地址是怎样定位到莽村附近的?
要说最近大火的电视剧非《狂飙》莫属。电视剧《狂飙》自开播以来,一举超过《三体》《去有风的地方》等先播电视剧,收视率一路“狂飙”,牢牢占据近期的收视冠军。 在剧中,张译扮演一名坚持公平、正义与理想的人民警察“安欣”&…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...
:邮件营销与用户参与度的关键指标优化指南)
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南 在数字化营销时代,邮件列表效度、用户参与度和网站性能等指标往往决定着创业公司的增长成败。今天,我们将深入解析邮件打开率、网站可用性、页面参与时…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...

安全突围:重塑内生安全体系:齐向东在2025年BCS大会的演讲
文章目录 前言第一部分:体系力量是突围之钥第一重困境是体系思想落地不畅。第二重困境是大小体系融合瓶颈。第三重困境是“小体系”运营梗阻。 第二部分:体系矛盾是突围之障一是数据孤岛的障碍。二是投入不足的障碍。三是新旧兼容难的障碍。 第三部分&am…...

群晖NAS如何在虚拟机创建飞牛NAS
套件中心下载安装Virtual Machine Manager 创建虚拟机 配置虚拟机 飞牛官网下载 https://iso.liveupdate.fnnas.com/x86_64/trim/fnos-0.9.2-863.iso 群晖NAS如何在虚拟机创建飞牛NAS - 个人信息分享...
