当前位置： 首页 > news >正文

数据结构 软考

news 2026/2/9 16:13:31

算法具有5个特性

可行性，有限性，确定性，输入, 输出

图:  有向图 Kruskal(克鲁斯卡尔)算法   和 prim(普鲁姆)算法  都是贪心算法

是一种用来在加权连通图中寻找最小生成树的算法,其操作对象是边.  找最小的不形成环

1.哈夫曼树(也叫最优树)

即叶子节点的带权路径长度最小 (树的第一层权就是0, 第二层就是1)
 

构造  19, 21, 2, 3，6, 7, 10, 32 的哈夫曼树，并计算WPL（带权路经长度）的值?

解题思路: 

带权路经长度计算公式 = 哈夫曼树每层的叶子节点 乘以 权, 然后相加即可

哈夫曼树特点: 从下往上,每一层从左到右递增, 取最小的2个向上构建，求和的结果放上去，把相加的2个数去掉,  不断的找最小的2个，直至所有的数都去掉，即构造完成

2.完全二叉树 / 满二叉树

完全二叉树（Complete Binary Tree）是一种特殊的二叉树，它的定义是：如果设二叉树的深度为h，除第h层外，其它各层（1~h-1）的结点数都达到最大个数，第h层所有的结点都连续集中在最左边，这就是完全二叉树

每层将节点尽量排满, 如果有空节点,则只在最后一层上,因此,树的高度相对其他二叉树一定是最小的

满二叉树:  每一层都达到最大个数

3. 平衡二叉树 

判断是否是平衡二叉树: 计算每个节点的平衡度(左子树高度减去右子树高度), 平衡度值是-1, 0, 1 , 说明是平衡二叉树, 否则是 非平衡二叉树

4.查找二叉树(也叫二叉排序树) 

左孩子节点 < 根  右孩子节点 > 根

5.线索二叉树

通过增设指针去保存节点的前驱后继关系

相关文章：

数据结构 软考

算法具有5个特性 可行性&#xff0c;有限性&#xff0c;确定性&#xff0c;输入, 输出 图: 有向图 Kruskal(克鲁斯卡尔)算法 和 prim(普鲁姆)算法 都是贪心算法 是一种用来在加权连通图中寻找最小生成树的算法,其操作对象是边. 找最小的不形成环 1.哈夫曼树(也叫最优树)…...

编程日记 2024/10/26 15:59:06

colcon构建ros2功能包时，出现exited with code 2报错的解决方案(bug)

背景&#xff1a; 在学习ros2时&#xff0c;跟着别人的示例进行构建&#xff0c;手敲的代码难免有一些语法错误。 问题&#xff1a; 在colcon构建时&#xff0c;并不会直接输出语法报错。而是出现exited with code 2错误&#xff0c;并提示未能生成功能包&#xff0c;就算加入…...

编程日记 2024/10/26 15:57:03

【大模型LLM面试合集】大语言模型架构_位置编码

位置编码 1.位置编码 不同于RNN、CNN等模型&#xff0c;对于Transformer模型来说&#xff0c;位置编码的加入是必不可少的&#xff0c;因为纯粹的Attention模块是无法捕捉输入顺序的&#xff0c;即无法区分不同位置的Token。为此我们大体有两个选择&#xff1a; 想办法将位置…...

编程日记 2024/10/26 15:54:01

FLINK 分流

在Apache Flink中&#xff0c;分流&#xff08;Stream Splitting&#xff09;是指将一条数据流拆分成完全独立的两条或多条流的过程。这通常基于一定的筛选条件&#xff0c;将符合条件的数据拣选出来并放入对应的流中。以下是关于Flink分流的详细解释&#xff1a; 一、分流方式…...

编程日记 2024/10/26 15:52:58

从零开始：构建一个高效的开源管理系统——使用 React 和 Ruoyi-Vue-Plus 的实战指南

✅作者简介&#xff1a;2022年博客新星 第八。热爱国学的Java后端开发者&#xff0c;修心和技术同步精进。 &#x1f34e;个人主页&#xff1a;Java Fans的博客 &#x1f34a;个人信条&#xff1a;不迁怒&#xff0c;不贰过。小知识&#xff0c;大智慧。 &#x1f49e;当前专栏…...

编程日记 2024/10/26 15:51:57

windows下pycharm社区版2024下载与安装（包含新建第一个工程）

windows下pycharm社区版2024下载与安装 下载pycharm pycharm官网 安装pycharm 1.进入官网 pycharm官网 下载 点击Download–>右侧Other versions 下载对应的社区版&#xff08;如下图&#xff09;&#xff1a;下载网址 2.点击运行下载好的安装包 点击下一步 3.更改pychar…...

编程日记 2024/10/26 15:47:54

重构案例：将纯HTML/JS项目迁移到Webpack

我们已经了解了许多关于 Webpack 的知识&#xff0c;但要完全熟练掌握它并非易事。一个很好的学习方法是通过实际项目练习。当我们对 Webpack 的配置有了足够的理解后&#xff0c;就可以尝试重构一些项目。本次我选择了一个纯HTML/JS的PC项目进行重构&#xff0c;项目位于 GitH…...

编程日记 2024/10/26 15:46:53

表格编辑demo

<el-form :model"form" :rules"status ? rules : {}" ref"form" class"form-container" :inline"true"><el-table :data"tableData"><el-table-column label"计算公式"><templat…...

编程日记 2024/10/26 15:43:49

企业自建邮件系统选U-Mail ，功能强大、安全稳定

在现代企业运营中&#xff0c;电子邮件扮演着至关重要的角色&#xff0c;随着企业规模的增长和业务的多样化&#xff0c;传统的租用第三方企业邮箱服务逐渐显现出其局限性。例如&#xff0c;存储空间受限、数据安全风险、缺乏灵活的管理和备份功能&#xff0c;以及无法与其他企…...

编程日记 2024/10/26 15:42:48

蓝桥杯题目理解

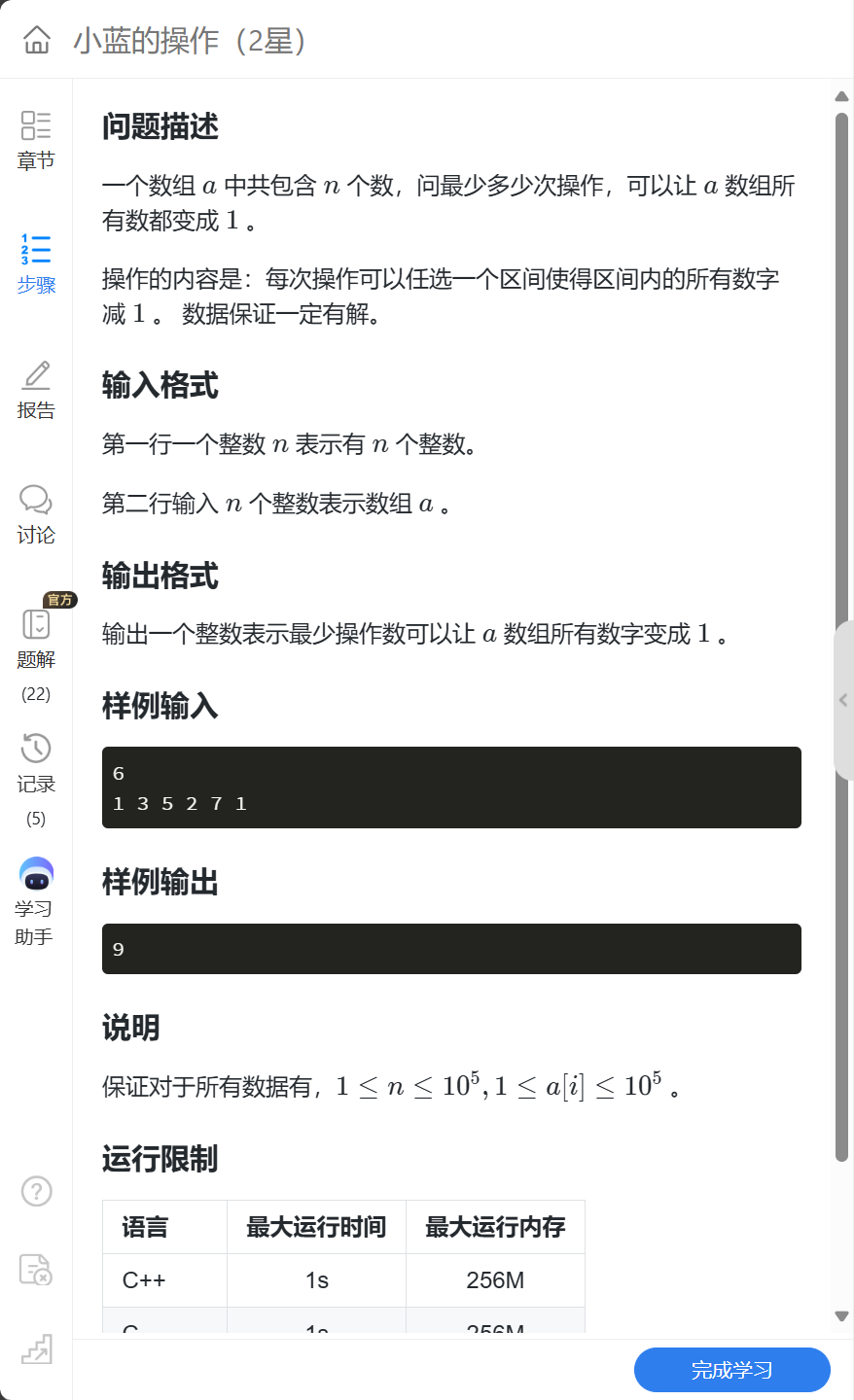
1. 一维差分 1.1. 小蓝的操作 1.1.1. 题目解析&#xff1a; 这道题提到了对于“区间”进行操作&#xff0c;而差分数列就是对于区间进行操作的好方法。 观察差分数列&#xff1a; 给定数列&#xff1a;1 3 5 2 7 1 差分数列&#xff1a;1 2 2 -3 5 6 题目要求把原数组全部…...

编程日记 2024/10/26 15:38:46

浪潮云启操作系统（InLinux）bcache缓存实践：理解OpenStack环境下虚拟机卷、Ceph OSD、bcache设备之间的映射关系

前言 在OpenStack平台上&#xff0c;采用bcache加速ceph分布式存储的方案被广泛用于企业和云环境。一方面&#xff0c;Ceph作为分布式存储系统&#xff0c;与虚拟机存储卷紧密结合&#xff0c;可以提供高可用和高性能的存储服务。另一方面&#xff0c;bcache作为混合存储方案&…...

编程日记 2024/10/26 15:35:42

通过ssh端口反向通道建立并实现linux系统的xrdp以及web访问

Content 1 问题描述2 原因分析3 解决办法3.1 安装x11以及gnome桌面环境查看是否安装x11否则使用下面指令安装x11组件查看是否安装gnome否则使用下面指令安装gnome桌面环境 3.2 安装xrdp使用下面指令安装xrdp&#xff08;如果安装了则跳过&#xff09;启动xrdp服务 3.3 远程服务…...

编程日记 2024/10/26 15:27:34

# 渗透测试#安全见闻8 量子物理面临的安全挑战

# 渗透测试#安全见闻8 量子物理面临的安全挑战 ##B站陇羽Sec## 量子计算原理与技术 量子计算是一种基于量子力学原理的计算方式&#xff0c;它利用量子位&#xff08;qubits&#xff09;来进行信息处理和计算…...

编程日记 2024/10/26 15:24:29

【rabbitmq】实现问答消息消费示例

目录 1. 说明2. 截图2.1 接口调用截图2.2 项目结构截图 3. 代码示例 1. 说明 1.实现的是一个简单的sse接口&#xff0c;单向的长连接&#xff0c;后端可以向前端不断输出数据。2.通过调用sse接口&#xff0c;触发rabbitmq向队列塞消息&#xff0c;向前端返回一个sseEmitter对象…...

编程日记 2024/10/26 15:23:28

单片机_RTOS__架构概念

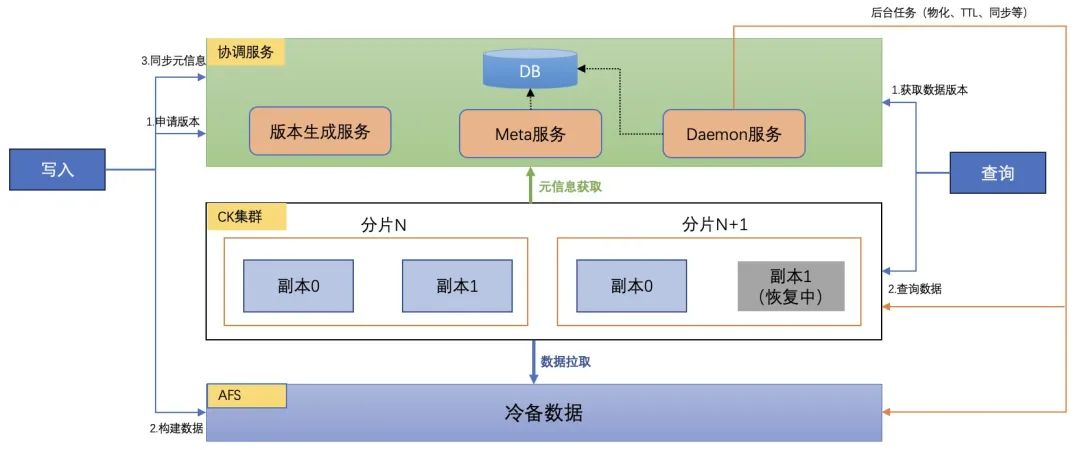
经典单片机程序 void main() {while(1){函数1&#xff08;&#xff09;&#xff1b;函数2&#xff08;&#xff09;&#xff1b;}} 有无RTOS区别 裸机 RTOS RTOS程序 喂饭&#xff08;&#xff09; {while&#xff08;1&#xff09;{喂一口饭&#xff08;&#xff09;;} } …...

编程日记 2024/10/26 15:16:19

ClickHouse在百度MEG数据中台的落地和优化

导读 百度MEG上一代大数据产品存在平台分散、质量不均和易用性差等问题&#xff0c;导致开发效率低下、学习成本高&#xff0c;业务需求响应迟缓。为了解决这些问题&#xff0c;百度MEG内部开发了图灵3.0生态系统&#xff0c;包括Turing Data Engine(TDE)计算引擎、Turing Dat…...

编程日记 2024/10/26 15:14:17

B/S架构（Browser/Server）与C/S架构（Client/Server）

基本概念 B/S架构&#xff08;Browser/Server&#xff09;&#xff1a;即浏览器/服务器架构。在这种架构中&#xff0c;用户通过浏览器&#xff08;如Chrome、Firefox、Safari等&#xff09;访问服务器上的应用程序。服务器端负责处理业务逻辑、存储数据等核心功能&#xff0c;…...

编程日记 2024/10/26 15:13:17

idea中自定义注释模板语法

文章目录 idea 自定义模板语法1.自定义模板语法是什么&#xff1f;2.如何在idea中设置呢&#xff1f; idea 自定义模板语法 1.自定义模板语法是什么&#xff1f; 打开我的idea&#xff0c;创建一个测试类&#xff1a; 这里看到我的 test 测试类里面会有注释&#xff0c;这是怎…...

编程日记 2024/10/26 15:12:14

基于SSM的儿童教育网站【附源码】

基于SpringBoot的课程作业管理系统&#xff08;源码L文说明文档&#xff09; 目录 4 系统设计 4.1 系统概述 4.2 系统模块设计 4.3.3 数据库表设计 5 系统实现 5.1 管理员功能模块的实现 5.1.1 视频列表 5.1.2 文章信息管理 5.1.3 文章类…...

编程日记 2024/10/26 15:11:12

深挖自闭症病因与孩子表现的关联

自闭症&#xff0c;亦称为孤独症&#xff0c;乃是一种对儿童发展有着严重影响的神经发育障碍性疾病。深入探寻自闭症的病因与孩子表现之间的联系&#xff0c;对于更深刻地理解并助力自闭症儿童而言&#xff0c;可谓至关重要。 当前&#xff0c;自闭症的病因尚未完全明晰&#x…...

编程日记 2024/10/26 15:07:07

浏览器访问 AWS ECS 上部署的 Docker 容器（监听 80 端口）

✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义&#xff08;Task Definition&…...

编程新知 2026/2/8 15:03:14

生成xcframework

打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式&#xff0c;可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

编程新知 2025/10/5 2:30:38

阿里云ACP云计算备考笔记 (5)——弹性伸缩

目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

编程新知 2026/1/22 6:07:24

五年级数学知识边界总结思考-下册

目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解&#xff1a;由来、作用与意义**一、知识点核心内容****二、知识点的由来&#xff1a;从生活实践到数学抽象****三、知识的作用&#xff1a;解决实际问题的工具****四、学习的意义&#xff1a;培养核心素养…...

编程新知 2025/10/7 4:57:55

P3 QT项目----记事本（3.8）

3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

编程新知 2026/2/1 6:56:36

三体问题详解

从物理学角度&#xff0c;三体问题之所以不稳定&#xff0c;是因为三个天体在万有引力作用下相互作用&#xff0c;形成一个非线性耦合系统。我们可以从牛顿经典力学出发&#xff0c;列出具体的运动方程&#xff0c;并说明为何这个系统本质上是混沌的&#xff0c;无法得到一般解…...

编程新知 2025/10/19 5:14:05

GC1808高性能24位立体声音频ADC芯片解析

1. 芯片概述 GC1808是一款24位立体声音频模数转换器&#xff08;ADC&#xff09;&#xff0c;支持8kHz~96kHz采样率&#xff0c;集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器&#xff0c;适用于高保真音频采集场景。 2. 核心特性 高精度&#xff1a;24位分辨率&#xff0c…...

编程新知 2026/1/27 4:58:14

基于matlab策略迭代和值迭代法的动态规划

经典的基于策略迭代和值迭代法的动态规划matlab代码&#xff0c;实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...

编程新知 2025/12/7 23:28:25

智能AI电话机器人系统的识别能力现状与发展水平

一、引言 随着人工智能技术的飞速发展&#xff0c;AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术&#xff0c;在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

编程新知 2025/6/11 3:05:02

【Nginx】使用 Nginx+Lua 实现基于 IP 的访问频率限制

使用 NginxLua 实现基于 IP 的访问频率限制 在高并发场景下&#xff0c;限制某个 IP 的访问频率是非常重要的&#xff0c;可以有效防止恶意攻击或错误配置导致的服务宕机。以下是一个详细的实现方案&#xff0c;使用 Nginx 和 Lua 脚本结合 Redis 来实现基于 IP 的访问频率限制…...

编程新知 2025/10/22 6:06:44