川渝地区软件工程考研择校分析
C哥专业提供——计软考研院校选择分析+专业课备考指南规划
通过最新数据分析,5所高校软件工程专业2025年考研难度从高到低预计为:
电子科技大学 >> 四川大学 > 重庆大学 ≈ 西南交通大学 > 西南大学
对于想考川渝地区985但核心目标为优先上岸的考生,建议重点考虑西南交通大学软件工程学硕。该校24届软件工程学硕实际录取13人,复试线356分,报考人数适中,专业实力较强,就业前景好,具有较高性价比[1]。
二、"三元法"定性分析
1. 学校排名与声誉
-
电子科技大学(全国第28名)
-
四川大学(全国第37名)
-
重庆大学(全国第39名)
-
西南交通大学(全国第41名)
-
西南大学(全国第91名)
2. 专业排名与实力
-
电子科技大学软件工程全国前15
-
四川大学软件工程全国前25
-
重庆大学软件工程全国前35
-
西南交通大学软件工程全国前40
-
西南大学软件工程全国前60
3. 地理位置优势
成都地区(电子科技大学、四川大学):
-
西部软件产业中心
-
腾讯、字节跳动、百度等知名企业设立分部
-
就业机会丰富
重庆地区(重庆大学、西南大学):
-
新兴软件产业基地
-
互联网产业快速发展
-
人力成本优势
4. 三元法分析小结
从综合实力来看,电子科技大学软件工程优势显著,四川大学次之,重庆大学和西南交通大学相当,西南大学实力相对较弱。
三、定量分析
1. 考试科目对比
各校基本科目设置:
-
公共课:政治、英语一
-
数学:数学一
-
专业课:数据结构、操作系统等,各校命题
2. 研究方向对比
主要研究方向包括:
-
软件工程理论与方法
-
人工智能与知识工程
-
大数据分析与云计算
-
软件测试与质量保证
-
嵌入式软件与系统开发
3. 考研报录数据分析
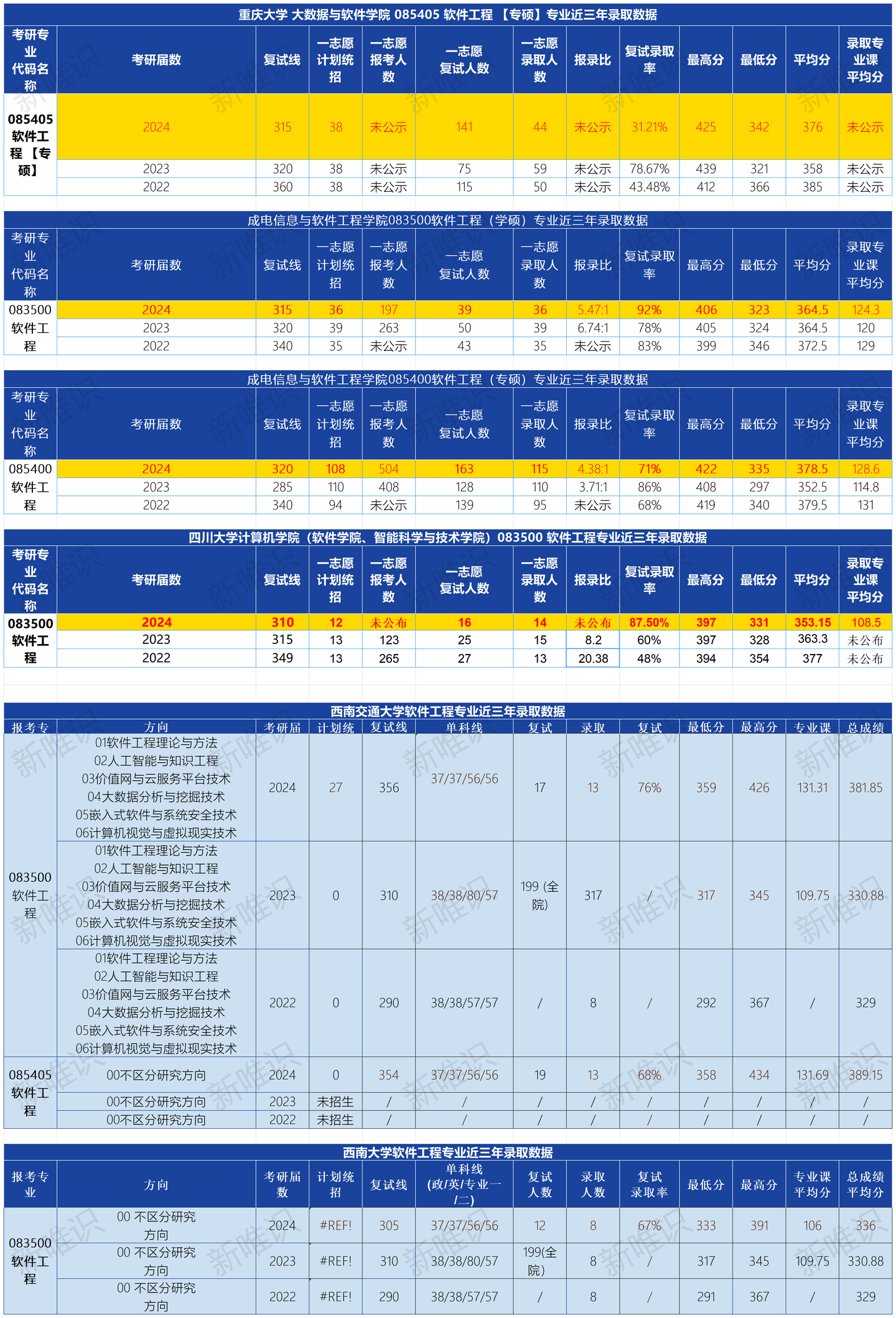
电子科技大学
学硕分析:
-
计划招生36人,实际复试39人,录取36人,复试录取率92%
-
复试线315分,较去年降低5分
-
350分以上基本能录取,录取分数分布较为集中
专硕分析:
-
计划招生108人,实际复试163人,录取115人
-
复试线320分,较去年提高35分
-
350-379分段录取率较高
四川大学
学硕分析:
-
复试16人,录取14人,复试录取率87.5%
-
复试线310分,较去年略降
-
330分以上录取率较高,录取分数分布较为均匀
重庆大学
学硕分析:
-
复试30人,录取7人,复试录取率23.33%
-
复试线315分,与去年持平
-
录取分数普遍在340分以上
专硕分析:
-
复试141人,录取44人,复试录取率31.21%
-
复试线315分,较去年下降5分
-
380分以上录取概率较大
西南交通大学
学硕分析:
-
复试17人,录取13人,复试录取率76.47%
-
复试线356分,较去年显著提高
-
录取分数分布较为集中
专硕分析:
-
复试19人,录取13人,复试录取率68.42%
-
复试线354分
-
首次招生,关注度较低
西南大学
学硕分析:
-
复试12人,录取8人,复试录取率67%
-
复试线305分,较去年略降
-
录取分数相对较低,330-350分录取率高

4. 综合分析建议
-
基础很强的考生(预期380+): 建议报考电子科技大学学硕,虽然竞争激烈但出身好、就业好。
-
基础较好的考生(预期350-380): 优先推荐西南交通大学学硕,今年录取分数虽然偏高但关注度不高,具有较高性价比。其次可考虑四川大学学硕。
-
基础一般的考生(预期330-350): 建议报考西南大学学硕,录取难度相对较低,考研成功率较高。
-
想求稳的考生: 建议报考电子科技大学专硕,招生人数多,虽然进复试难但过线后录取率较高。
四、25考研分数线预测
-
电子科技大学:学硕320左右,专硕325左右,稳中略升
-
四川大学:315左右,稳中有升
-
重庆大学:学硕320左右,专硕320左右,大概率稳定
-
西南交通大学:学硕360左右,专硕355左右,稳中略升
-
西南大学:310左右,稳中有升
考虑到软件行业就业形势向好,且25届考研人数可能略有下降[2],建议优先考虑西南交通大学软件工程学硕。具体原因如下:
-
该校软件工程24届录取分布合理,过线基本能录取
-
专业实力较强,就业前景好
-
竞争压力相对较小,性价比高
-
建议目标分数360+
希望C哥的文章能够帮到大家更清晰明了计算机软件的考研院校选择解决考研相关问题;
需计软考研院校选择规划及备考指南,欢迎找C哥唠嗑儿~
也祝大家都能金榜题名,一战上岸!
相关文章:

川渝地区软件工程考研择校分析
C哥专业提供——计软考研院校选择分析专业课备考指南规划 通过最新数据分析,5所高校软件工程专业2025年考研难度从高到低预计为: 电子科技大学 >> 四川大学 > 重庆大学 ≈ 西南交通大学 > 西南大学 对于想考川渝地区985但核心目标为优先上岸的考生,建议重点考虑西…...

快捷键记忆
快捷键记忆 文章目录 快捷键记忆前言一、PotPlayer快捷键二、电脑快捷键总结 前言 提示:以下是本篇文章正文内容: 一些软件的快捷键经常忘记,写这篇文章的目的是帮助我忘记的时候来查看。 顺序实时更新: 一、PotPlayer快捷键 Po…...

Flutter鸿蒙next 状态管理高级使用:深入探讨 Provider
✅近期推荐:求职神器 https://bbs.csdn.net/topics/619384540 🔥欢迎大家订阅系列专栏:flutter_鸿蒙next 💬淼学派语录:只有不断的否认自己和肯定自己,才能走出弯曲不平的泥泞路,因为平坦的大路…...

JMeter实战之——模拟登录
本篇介绍使用JMeter 如何对需要登录的站点进行压力测试。 基本Session验证的机制 使用session进行请求验证的机制是一种常见的Web应用认证方式。 该认证方式的主要内容如下: 一、登录过程 用户输入:用户在登录页面输入用户名和密码。发送请求&#x…...

智能台灯设计(一)原理图设计
1. 前言 作者最近突发奇想,想自己做一个小台灯,设想的功能有:带锂电池可充电、可以调节亮度,后续通过增加WIFI模块实现手机控制开关功能。目前先实现最简单的功能,有时间再一步步完善吧。 2. 原理图设计 充电芯片使用…...

数据库查询返回结果集及其元数据信息:ResultSet 和 ResultSetMetaData 深度解析
全文目录: 开篇语📌 目录🌟 前言📝 摘要📚 简介🔍 概述🧩 核心源码解读1️⃣ 创建数据库连接2️⃣ 执行查询获取结果集3️⃣ 读取查询数据4️⃣ 获取元数据信息 💻 案例分析…...

2.插入排序(斗地主起牌)
一、思想 扑克牌起牌 代码: 二、时间复杂度: 最好情况(已经排序好的):T O(N) 最坏情况(完全逆序):T O(N^2) 三、优劣: 严格的大小比较之后才进行错位插入&#x…...

漫谈编程小白如何成为大神:夯实基础,开启通神之路
在当今数字化时代,编程已成为一项基本技能,对于大学新生而言,掌握编程能力不仅能够为学术研究提供支持,还能为未来的职业生涯开辟广阔天地。然而,面对琳琅满目的编程语言和学习资源,新生们往往会感到迷茫和…...

基于机器学习的个性化电影推荐系统【源码+安装+讲解+售后+文档】
【1】系统介绍 研究背景 随着互联网技术的迅速发展,数字娱乐内容特别是电影和电视剧的数量急剧增加。用户在享受丰富内容的同时,也面临着选择困难的问题,即“信息过载”。传统的搜索和分类方法已经无法满足用户日益增长的个性化需求。与此同…...

企业如何配合好等级保护测评工作?
企业如何配合好等级保护测评工作,是一个涉及多方面因素的系统性任务。等级保护测评,简称等保测评,是中国对信息和信息系统安全的重要管理手段和评估制度。通过这一制度,企业可以全面了解其信息系统的安全状况,及时发现…...

Could not find artifact cn.hutool:hutool-all:jar:8.1 in central 导入Hutool报错
<!-- https://mvnrepository.com/artifact/cn.hutool/hutool-all --><dependency><groupId>cn.hutool</groupId><artifactId>hutool-all</artifactId><version>5.8.9</version></dependency> 引入hutool 8.1版本的工具…...

【功能安全】汽车功能安全个人认证证书
目录 1、证书 2、课程信息 📖 推荐阅读 1、证书 汽车功能安全工程师去拿类似莱茵、SGS、南德颁发的证书,如下: 2、课程信息 一般上什么课程了,课程信息大概如下: 汽车功能安全工程师认证课 (3天&#…...

axios直接上传binary
axios直接上传二进制文件 、 axios直接上传apk、axios直接上传binary postman中的参数选项中有个binary,平常我们很少使用,可能有的同学遇到这种情况不太会了,认为后端应该有个字段名来接收,或者使用 Formdata,但其实…...

量化交易API接口是什么?如何申请和应用?
炒股自动化:申请官方API接口,散户也可以 python炒股自动化(0),申请券商API接口 python炒股自动化(1),量化交易接口区别 Python炒股自动化(2):获取…...

语义分割:YOLOv11的分割模型训练自己的数据集(从代码下载到实例测试)
文章目录 前言一、环境搭建二、构建数据集三、修改配置文件①数据集文件配置②模型文件配置 四、模型训练和测试模型训练模型验证模型推理 总结 前言 专栏目录:YOLOv11改进目录一览 | 涉及卷积层、轻量化、注意力、损失函数、Backbone、SPPF、Neck、检测头等全方位改…...

Python爬虫:从入门到精通
Python爬虫:从入门到精通 在数字时代,信息就如同水源,源源不绝。然而,当你想要从海量的信息中汲取有价值的“水”,你会发现这并不是一件容易的事。这就是为什么网络爬虫出现了。它们帮助我们在网络的海洋中航行&#…...

Web组态软件
Web组态软件是近年来前端开发领域的一股新兴力量,它以其独特的魅力吸引着越来越多的开发者们。那么,Web组态软件到底是什么?它有哪些特点?我们又该如何选择和使用它呢?下面,就让我们一起探讨这些问题。 一…...

Java中为什么要私有化构造方法
为什么要私有化构造方法 要私有化的方法不是来描述一类事物的,创建没有任何意义 解决方案: 提示:这里填写该问题的具体解决方案: 为什么要将构造方法私有化? 问:如果要限制一个类对象产生,即&…...

【大数据学习 | kafka】kafuka的基础架构
1. kafka是什么 Kafka是由LinkedIn开发的一个分布式的消息队列。它是一款开源的、轻量级的、分布式、可分区和具有复制备份的(Replicated)、基于ZooKeeper的协调管理的分布式流平台的功能强大的消息系统。与传统的消息系统相比,KafKa能够很好…...
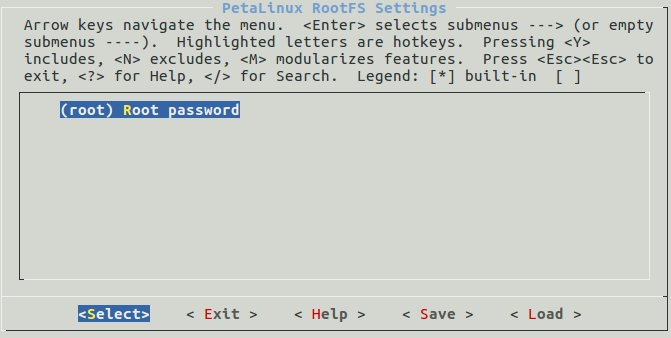
2-petalinux2018.3摸索记录-petalinux rootfs
1Filesystem Packages文件系统软件包2Petalinux Package GroupsPetalinux软件包组3Image Features镜像特性4apps应用程序5user packages用户软件包6Petalinux RootFS SettingsPetalinux根文件系统设置 Filesystem Packages(文件系统软件包) 这个选项主要…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...

R语言速释制剂QBD解决方案之三
本文是《Quality by Design for ANDAs: An Example for Immediate-Release Dosage Forms》第一个处方的R语言解决方案。 第一个处方研究评估原料药粒径分布、MCC/Lactose比例、崩解剂用量对制剂CQAs的影响。 第二处方研究用于理解颗粒外加硬脂酸镁和滑石粉对片剂质量和可生产…...

GruntJS-前端自动化任务运行器从入门到实战
Grunt 完全指南:从入门到实战 一、Grunt 是什么? Grunt是一个基于 Node.js 的前端自动化任务运行器,主要用于自动化执行项目开发中重复性高的任务,例如文件压缩、代码编译、语法检查、单元测试、文件合并等。通过配置简洁的任务…...

Java求职者面试指南:计算机基础与源码原理深度解析
Java求职者面试指南:计算机基础与源码原理深度解析 第一轮提问:基础概念问题 1. 请解释什么是进程和线程的区别? 面试官:进程是程序的一次执行过程,是系统进行资源分配和调度的基本单位;而线程是进程中的…...

GO协程(Goroutine)问题总结
在使用Go语言来编写代码时,遇到的一些问题总结一下 [参考文档]:https://www.topgoer.com/%E5%B9%B6%E5%8F%91%E7%BC%96%E7%A8%8B/goroutine.html 1. main()函数默认的Goroutine 场景再现: 今天在看到这个教程的时候,在自己的电…...
