C++二级题 计算好数:1数大于0数(二进制的位运算)
1、题目
若将一个正整数化为二进制数,在此二进制数中,我们将数字1的个数多于数字0的个数的这类二进制数称为好数。
例如:
(13)10 = (1101)2,其中1的个数为3,0的个数为1,则此数是好数;
(10)10 = (1010)2,其中1的个数为2,0的个数也为2,则此数不是好数;
(24)10 = (11000)2,其中1的个数为2,0的个数为3,则此数不是好数;
对于给定的N,写程序求出1~N之中(包括1与N)中的好数个数。
时间限制:1000
内存限制:65536
输入
一个整数,题目中的N(N ≤ 1000)
输出
一个整数,表示1~N之中(包括1与N)中的好数个数
样例输入
10样例输出
5
2、提示
提示:
(1)n>>=1 二进制右移一位
n>>=1表示将变量n的二进制表示向右移动一位,并将结果赋值给n。
具体来说,n>>=1的操作过程是将n的二进制表示向右移动一位,最右边的位会被丢弃,而最左边的位会填充为0。这个过程相当于将n除以2并取整。例如,如果n=8(二进制表示为1000),那么n>>=1后,n的值将变为4(二进制表示为100)。
这种操作在位运算中非常常见,可以用于各种算法和数据处理中。例如,在统计一个无符号整数的二进制表示中有多少个1时,可以通过连续地将结果左移并添加原始数最右边的位,然后将原始数右移,有效地反转了位。
(2)n&1 用来找二进制最低位数/奇数
在C++中,表达式n&1用于判断n是否为奇数。
如果n为奇数,n的二进制表示的最低位为1,因此n&1的结果为1;如果n为偶数,n的二进制表示的最低位为0,因此n&1的结果为0。
这种判断方法利用了二进制运算的性质。在二进制表示中,奇数的最低位为1,偶数的最低位为0。因此,通过将n与1进行按位与操作(&),可以快速判断n的奇偶性。具体来说,1的二进制表示为000...01,与n进行按位与操作后,只有当n的最低位为1时,结果才为1,否则为0。
(3)比特右移(>>)运算符可以是算术(左端补最高有效位)或是逻辑(左端补 0)位移。
3、代码
#include <bits/stdc++.h>
using namespace std;
bool is_good(int n){int a=0,b=0;while(n){if(n&1) a++;else b++;n>>=1;}return a>b?true:false;
}
int main(){int n,counts=0;cin>>n;for(int i=1;i<=n;i++)if(is_good(i)) counts++;cout<<counts;return 0;
}相关文章:
)
C++二级题 计算好数:1数大于0数(二进制的位运算)
1、题目 若将一个正整数化为二进制数,在此二进制数中,我们将数字1的个数多于数字0的个数的这类二进制数称为好数。 例如: (13)10 (1101)2,其中1的个数为3,0的个数为1,则此数是好数; (10)10 (1…...

数字孪生城市:智慧城市的未来蓝图
在当今数字化时代,智能技术的广泛应用正在改变人们的生活和工作方式。数字孪生城市作为未来新型智慧城市演进的重要方向,数字孪生城市是一种将城市物理世界的各个方面转化为数字形式的技术,通过网络空间与物理世界之间的实时数据交换和仿真分…...

Java篇图书管理系统
目录 前言 一. 图书管理系统的核心 二. 图书管理系统基本框架 2.1 book包 2.1.1 Book(书籍类) 2.1.2 Booklist (书架类) 2.2 user包 2.2.1 User类 2.2.2 Administrator(管理员类) 2.2.3 Visitor(用户类) 2.…...

BUUCTF之web篇
第一题 [极客大挑战 2019]EasySQL 打开靶机后可以看到这是一个登陆的页面 我们可以尝试两种方式登录 弱口令爆破(burpsuite) 通过SQL注入里的万能密码来跳过账户和密码验证的过程 这里就需要万能密码aor true # 在这里单引号的作用是结束用户名或者密码…...
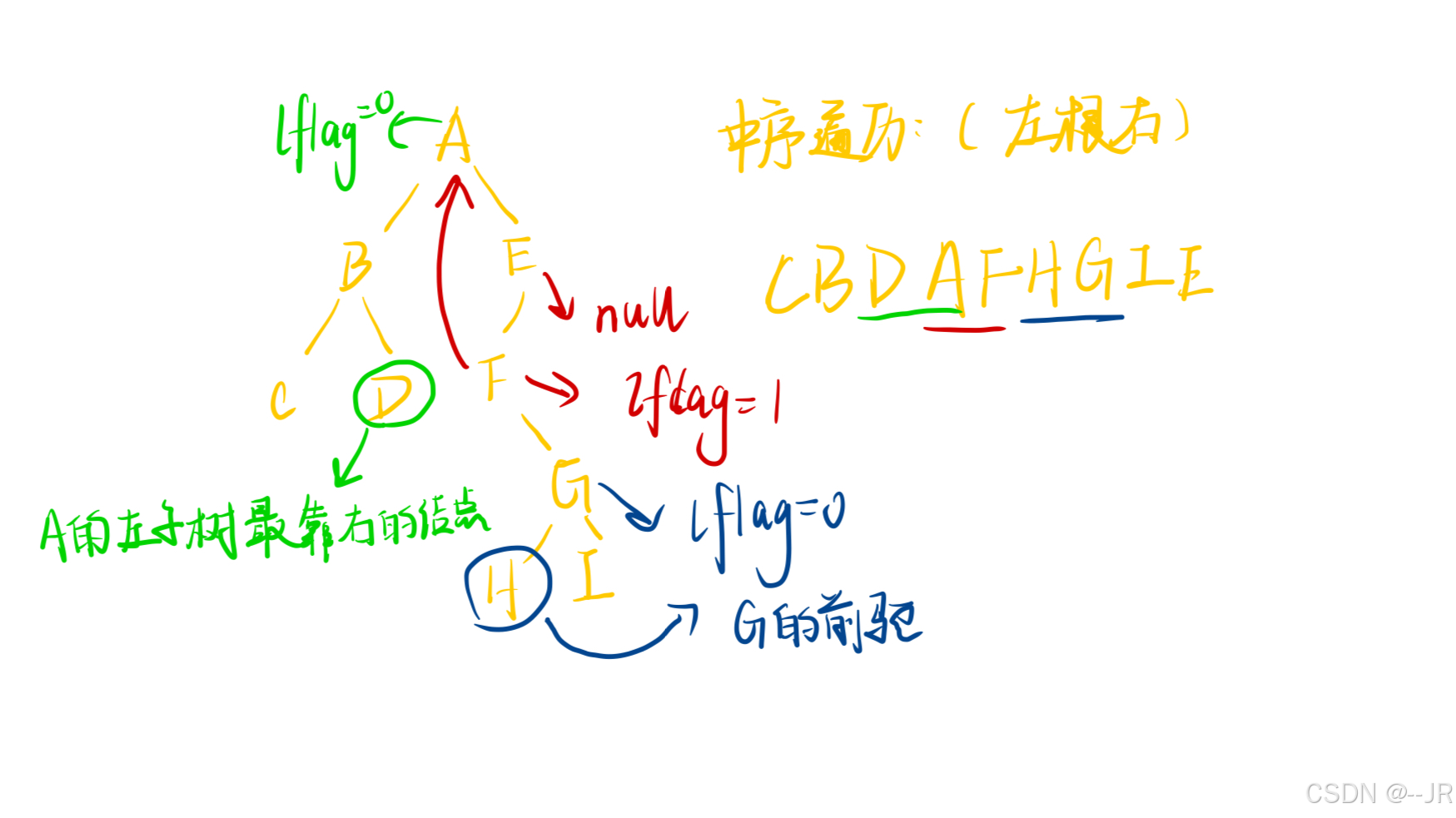
010——二叉树(2)线索化
引入: 问题1: n个节点的二叉树,用二叉链表存储,问在这个二叉链表中一共有 __个指针域? 其中,有 __个指针域不为NULL,__个指针域为NULL? 答:2n n-1 n1 在二叉链表中…...

鸿蒙拍照小助手02
项目文件目录 为了确保项目文件目录清晰,以下是完整的项目文件目录结构: code 拍照小助手/ │ ├── entry/ │ ├── src/ │ │ ├── main/ │ │ │ ├── js/ │ │ │ │ └── 默认/ │ │ │ │ ├── 页面/ │ │ │ │ │ ├── 主页/ │ │ │ │ │ │ ├…...

lua while循环
软考鸭微信小程序 过软考,来软考鸭! 提供软考免费软考讲解视频、题库、软考试题、软考模考、软考查分、软考咨询等服务 Lua作为一种小巧精致的语言,特别适用于嵌入其他程序提供脚本支持。在编程中,循环结构是不可或缺的一部分,而while循环则是…...

JAVA篇之类和对象
目录 一. 面向对象 1.1 面向对象和面向过程 二. 类的定义和使用 2.1 什么是类 2.2 类的定义格式 三. 类的实例化 四. this引用 4.1 this引用的作用 五. 构造方法 5.1 构造方法重载 5.2 通过this调用其他构造方法 5.3 默认初始化 结语 一. 面向对象 Java 是一门面向对…...

IO流详解_CoderLix
主要内容 File类IO流字节流字符流异常处理Properties缓冲流转换流序列化流打印流 File类 1.1 概述 java.io.File 类是文件和目录路径名的抽象表示,主要用于文件和目录的创建、查找和删除等操作。 1.2 构造方法 public File(String pathname) :通过…...
241023-RHEL非管理员安装Docker并开放指定宿主机端口部署Gitlab
A. RHEL非管理员安装Docker 要在没有管理员权限的情况下离线安装 Docker 和 Docker Compose,虽然受到一定限制,仍有一些可行的步骤可以帮助你在有限权限下完成这项任务。需要注意的是,这种方式适用于本地用户环境下的 Docker 安装࿰…...

python ubuntu安装加速
ubuntu升级python到python3.11(可能是全网最靠谱的方法,亲测有效)_ubuntu python3.11-CSDN博客 python-release安装包下载_开源镜像站-阿里云...

100种算法【Python版】第12篇——快速幂算法
本文目录 1 基本原理2 基本步骤3 数学示例4 python代码1 基本原理 快速幂算法(Fast Exponentiation)是一种高效计算整数幂的方法,尤其适用于计算大数的幂。其主要思想是利用分治法和二进制表示来减少乘法运算的次数,从而加快计算速度。 计算 x n x^n x...

Java多线程详解②(全程干货!!!)Thread Runnable
这里是Themberfue 上节主要讲完了多线程的一些基础知识,这节通过代码进一步理解多线程🫡 多线程 Java标准库中提供了Thread类,以程序员们编写多线程代码,我们可以查看官方文档进一步了解Thread的特性以及提供的接口。 类似于Sy…...

机器学习——图神经网络
图神经网络(GNN):理解复杂网络数据的有效工具 图神经网络(Graph Neural Network, GNN)是近年来机器学习领域的热门话题。GNN 以图结构数据为核心,能够高效地捕捉节点和边的复杂关系,广泛应用于社交网络、推荐系统、生…...

一、在cubemx下RTC配置调试实例测试
一、rtc的时钟有lse提供。 二、选择rtc唤醒与闹钟功能 内部参数介绍 闹钟配置 在配置时间时,注意将时间信息存储起来,防止复位后时间重新配置。 if(HAL_RTCEx_BKUPRead(&hrtc, RTC_BKP_DR0)! 0x55AA)//判断标志位是否配置过,没有则进…...

【Nas】X-DOC:Mac mini Docker部署中国特供版Jellyfin
【Nas】X-DOC:Mac mini Docker部署中国特供版Jellyfin 1、拉取镜像:2、启动镜像3、访问服务4、参考文档 Mac mini Docker部署中国特供版Jellyfin 1、拉取镜像: docker pull nyanmisaka/jellyfin:230901-amd64jellyfin 10.8.10版本ÿ…...

合合信息:生成式Al时代的内容安全与系统构建加速,开启智能文档的全新潜能
文章目录 写在前面图像内容安全图像篡改应用场景伪造文档/证照检测伪造人脸检测 GAI时代系统构建加速通用文档解析 合合信息 写在前面 随着人工智能技术的飞速发展,生成式AI已经悄然步入了我们的日常生活,以其强大的内容生成能力,重塑了信息…...

京东双十一高并发场景下的分布式锁性能优化
背景 在电商领域,尤其是像京东双十一这样的大促活动,系统需要处理极高的并发请求。这些请求往往涉及库存的查询和更新,如果处理不当,很容易出现库存超卖、数据不一致等问题。分布式锁作为一种有效的解决方案,能够在多…...

华为ICT题库-AI 人工智能部分
1178、以下哪个选项是华为的云端AI芯片?(云服务考点) (A)Inferentia (B)MLU100 (C)Cloud TPU (D)Ascend 910 答案:D 解析:华为的云端AI芯片被称为Ascend芯片系列,其中Ascend 910是其旗舰产品。Ascend 910…...

React Native 修改安卓应用图片和名称
在React Native(RN)项目中,修改安卓应用图标和名称通常涉及对Android原生代码的一些修改。以下是详细步骤: 修改应用图标 准备图标资源: 创建或获取你想要的图标,并确保它们符合Android的图标规范…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...

html-<abbr> 缩写或首字母缩略词
定义与作用 <abbr> 标签用于表示缩写或首字母缩略词,它可以帮助用户更好地理解缩写的含义,尤其是对于那些不熟悉该缩写的用户。 title 属性的内容提供了缩写的详细说明。当用户将鼠标悬停在缩写上时,会显示一个提示框。 示例&#x…...

scikit-learn机器学习
# 同时添加如下代码, 这样每次环境(kernel)启动的时候只要运行下方代码即可: # Also add the following code, # so that every time the environment (kernel) starts, # just run the following code: import sys sys.path.append(/home/aistudio/external-libraries)机…...

MySQL 8.0 事务全面讲解
以下是一个结合两次回答的 MySQL 8.0 事务全面讲解,涵盖了事务的核心概念、操作示例、失败回滚、隔离级别、事务性 DDL 和 XA 事务等内容,并修正了查看隔离级别的命令。 MySQL 8.0 事务全面讲解 一、事务的核心概念(ACID) 事务是…...
