监督学习之逻辑回归
逻辑回归(Logistic Regression)
逻辑回归是一种用于二分类(binary classification)问题的统计模型。尽管其名称中有“回归”二字,但逻辑回归实际上用于分类任务。它的核心思想是通过将线性回归的输出映射到一个概率值,以进行类别预测。
1. 模型概述
逻辑回归的基本公式为:
P ( y = 1 ∣ x ) = σ ( z ) = 1 1 + e − z P(y=1|x) = \sigma(z) = \frac{1}{1 + e^{-z}} P(y=1∣x)=σ(z)=1+e−z1
其中:
- ( P ( y = 1 ∣ x P(y=1|x P(y=1∣x) ) 是给定特征 ( x x x ) 时,因变量 ( y y y ) 等于 1 的概率。
- ( z = β 0 z = \beta_0 z=β0 + β 1 x 1 \beta_1x_1 β1x1 + β 2 x 2 \beta_2 x_2 β2x2 + … \ldots … + β n x n \beta_n x_n βnxn ) 是线性组合。
- ( σ ( z ) \sigma(z) σ(z) ) 是 sigmoid 函数,将输出值映射到 0 0 0到 1 1 1之间。
2. Sigmoid 函数
Sigmoid 函数的形状如下:
σ ( z ) = 1 1 + e − z \sigma(z) = \frac{1}{1 + e^{-z}} σ(z)=1+e−z1
- 当 ( z z z ) 为负时,函数输出接近于 0 0 0;当 ( z z z ) 为正时,函数输出接近于 1 1 1。
- 这种特性使得 sigmoid 函数非常适合用于概率预测。
3. 损失函数
逻辑回归的损失函数为交叉熵损失(cross-entropy loss),用于衡量模型预测与实际标签之间的差异。其公式为:
L ( β ) = − 1 N ∑ i = 1 N [ y i log ( y ^ i ) + ( 1 − y i ) log ( 1 − y ^ i ) ] L(\beta) = -\frac{1}{N} \sum_{i=1}^{N} [y_i \log(\hat{y}_i) + (1-y_i) \log(1-\hat{y}_i)] L(β)=−N1i=1∑N[yilog(y^i)+(1−yi)log(1−y^i)]
其中:
- ( N N N ) 是样本数量。
- ( y i y_i yi ) 是实际标签。
- ( y ^ i \hat{y}_i y^i ) 是预测概率。
逻辑回归的损失函数求解通常通过 最大似然估计 和 梯度下降 等优化算法进行。逻辑回归模型中常用的损失函数是 交叉熵损失,目标是通过最小化损失函数来找到最佳的模型参数。
1. 逻辑回归中的损失函数
(1)损失函数
逻辑回归的损失函数基于交叉熵(Cross-Entropy Loss),用于衡量模型预测的概率分布与实际标签之间的差异。对于二分类问题,其形式为:
L ( β ) = − 1 N ∑ i = 1 N [ y i log ( y ^ i ) + ( 1 − y i ) log ( 1 − y ^ i ) ] L(\beta) = - \frac{1}{N} \sum_{i=1}^{N} \left[ y_i \log(\hat{y}_i) + (1 - y_i) \log(1 - \hat{y}_i) \right] L(β)=−N1i=1∑N[yilog(y^i)+(1−yi)log(1−y^i)]
其中:
- ( N N N ) 是样本数量。
- ( y i y_i yi ) 是第 ( i i i ) 个样本的真实标签( 0 0 0 或 1 1 1)。
- ( y ^ i = σ ( z i ) \hat{y}_i = \sigma(z_i) y^i=σ(zi) ) 是第 ( i i i ) 个样本的预测概率。
- ( z i = β 0 + β 1 x i 1 + β 2 x i 2 + ⋯ + β n x i n z_i = \beta_0 + \beta_1 x_{i1} + \beta_2 x_{i2} + \dots + \beta_n x_{in} zi=β0+β1xi1+β2xi2+⋯+βnxin ) 是线性组合。
- ( σ ( z ) \sigma(z) σ(z) ) 是 sigmoid 函数,定义为:
σ ( z ) = 1 1 + e − z \sigma(z) = \frac{1}{1 + e^{-z}} σ(z)=1+e−z1
这将线性回归的输出 ( z z z ) 映射到 ( ( 0 0 0, 1 1 1) ) 之间,作为类别为 1 1 1 的预测概率。
(2)如何求解损失函数
求解逻辑回归的损失函数通常使用 梯度下降 等优化方法。目标是找到使损失函数最小的参数 ( β \beta β ),即 最小化交叉熵损失。求解过程可以概括为以下步骤:
** 计算梯度**
为了最小化损失函数,我们需要对每个参数 ( β j \beta_j βj) 计算损失函数的偏导数(即梯度),并通过优化算法(如梯度下降)进行更新。
对于交叉熵损失函数,梯度计算公式为:
∂ L ∂ β j = − 1 N ∑ i = 1 N ( y i − y ^ i ) x i j \frac{\partial L}{\partial \beta_j} = -\frac{1}{N} \sum_{i=1}^{N} (y_i - \hat{y}_i) x_{ij} ∂βj∂L=−N1i=1∑N(yi−y^i)xij
其中:
- ( x i j x_{ij} xij ) 是第 ( i i i ) 个样本的第 ( j j j ) 个特征。
- ( y i y_i yi ) 是第 ( i i i ) 个样本的实际标签。
- ( y ^ i \hat{y}_i y^i) 是第 ( i i i ) 个样本的预测概率。
使用梯度下降更新参数 ,梯度下降法通过以下公式迭代更新参数:
β j = β j − α ∂ L ∂ β j \beta_j = \beta_j - \alpha \frac{\partial L}{\partial \beta_j} βj=βj−α∂βj∂L
其中:
- ( α \alpha α ) 是学习率(控制每次更新步长的大小)。
- ( ∂ L ∂ β j \frac{\partial L}{\partial \beta_j} ∂βj∂L ) 是损失函数对参数 ( β j \beta_j βj ) 的梯度。
通过不断更新参数,使得损失函数逐渐减小,直到达到全局或局部最优解。
(3) 代码示例:逻辑回归中的梯度下降
以下是使用 Python 实现逻辑回归梯度下降的示例:
import numpy as np# Sigmoid 函数
def sigmoid(z):return 1 / (1 + np.exp(-z))# 损失函数 (交叉熵)
def compute_loss(y, y_pred):return -np.mean(y * np.log(y_pred) + (1 - y) * np.log(1 - y_pred))# 梯度下降算法
def gradient_descent(X, y, learning_rate=0.1, num_iterations=1000):m, n = X.shapebeta = np.zeros(n) # 初始化参数for i in range(num_iterations):z = np.dot(X, beta)y_pred = sigmoid(z)gradients = np.dot(X.T, (y_pred - y)) / mbeta -= learning_rate * gradientsif i % 100 == 0:loss = compute_loss(y, y_pred)print(f"Iteration {i}: Loss = {loss}")return beta# 示例数据
X = np.array([[1, 2], [1, 3], [2, 2], [2, 3]]) # 样本数据
y = np.array([0, 0, 1, 1]) # 标签数据# 在样本数据前面加一列 1 用于偏置项 (截距项)
X_bias = np.c_[np.ones(X.shape[0]), X]# 运行梯度下降求解参数
beta = gradient_descent(X_bias, y)
print("求解得到的参数:", beta)
4. 优缺点
优点:
- 简单易懂:逻辑回归模型简单,易于实现和解释。
- 概率输出:模型输出的是预测的概率,可以用于更细致的决策。
- 适用于线性可分问题:在特征与目标变量之间存在线性关系时,表现良好。
缺点:
- 线性假设:假设特征与目标之间存在线性关系,不适用于复杂的非线性关系。辑回归假设特征和类别之间的关系是线性的,对于复杂非线性问题,表现不如其他模型(如决策树、神经网络)。
- 受特征选择影响:模型对输入特征敏感,需要合适的特征选择和处理。
- 容易过拟合:在特征数量较多时,可能会发生过拟合,特别是当样本量不足时。
- 无法解决多分类问题:标准的逻辑回归只适用于二分类问题,若要应用于多分类问题,需要使用 Softmax 回归或一对多策略。
5. 代码示例
以下是使用 Python 的 scikit-learn 库实现逻辑回归的示例:
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score, confusion_matrix, classification_report# 生成示例数据
X, y = make_classification(n_samples=100, n_features=2, n_classes=2, n_informative=2, n_redundant=0, random_state=42)# 拆分数据集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)# 创建逻辑回归模型
model = LogisticRegression()
model.fit(X_train, y_train)# 进行预测
y_pred = model.predict(X_test)# 评估模型
accuracy = accuracy_score(y_test, y_pred)
conf_matrix = confusion_matrix(y_test, y_pred)
class_report = classification_report(y_test, y_pred)print("准确率:", accuracy)
print("混淆矩阵:\n", conf_matrix)
print("分类报告:\n", class_report)# 绘制决策边界
plt.scatter(X[:, 0], X[:, 1], c=y, cmap='coolwarm', edgecolors='k')
xlim = plt.gca().get_xlim()
ylim = plt.gca().get_ylim()xx, yy = np.meshgrid(np.linspace(xlim[0], xlim[1], 100), np.linspace(ylim[0], ylim[1], 100))
Z = model.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)plt.contourf(xx, yy, Z, alpha=0.3, cmap='coolwarm')
plt.title('逻辑回归决策边界')
plt.xlabel('特征1')
plt.ylabel('特征2')
plt.show()
结果:


6. 总结
逻辑回归是一种简单而有效的分类模型,适合于解决二分类问题。尽管它有一些局限性(如线性假设),但在许多实际应用中,逻辑回归因其易于解释和实现而被广泛使用。通过合适的特征选择和数据处理,逻辑回归能够在很多情况下提供可靠的分类结果。
相关文章:

监督学习之逻辑回归
逻辑回归(Logistic Regression) 逻辑回归是一种用于二分类(binary classification)问题的统计模型。尽管其名称中有“回归”二字,但逻辑回归实际上用于分类任务。它的核心思想是通过将线性回归的输出映射到一个概率值…...
洛谷P1683-入门)
深度优先算法(DFS)洛谷P1683-入门
虽然洛谷是有题解的,但是你如果直接看得懂题解,你也不会来看这篇文章.. 这些代码均是我记录自身成长的记录,有写的不好的地方请谅解! 先上代码: #include <iostream> #include <vector> #include<iomanip> #include<cstdio&…...

Python数据分析基础
本文介绍了Python在数据分析中的应用,包括数据读取、清洗、处理和分析的基本操作。通过使用Pandas和Numpy库,我们可以高效地处理大量数据,并利用Matplotlib和Seaborn库进行数据可视化。 1. 引言 Python因其简洁的语法和强大的库支持&#x…...

《企业自设2-软件测试》线下课day3: 006扩展虚拟机
1.win11 修改hosts无权限 分别再cmd终端输入以下两行代码: C:\Windows\System32\drivers\etcnotepad hosts 2.先保存快照!!! 3.关闭虚拟机,将内存,CPU进行修改 就是再这个位置修改: 4.运…...
配置和排查 Lombok 在 IDEA 中使用的详细步骤
在日常开发中,Java 代码常常需要大量的样板代码,比如 getter、setter、toString 等方法。Lombok 是一个 Java 库,可以通过注解的方式,自动生成这些常见的代码,从而让代码更加简洁、清晰。比如,我们可以通过…...

JavaWeb合集18-接口管理Swager
十八、接口管理 1、Swager 使用Swagger你只需要按照它的规范去定义接口及接口相关的信息,就可以做到生成接口文档,以及在线接口调试页面。 官网: https://swagger.io/ Knife4j是为Java MVC框架集成Swagger生成Api文档的增强解决方案。 <dependency&g…...

背包九讲——二维费用背包问题
目录 二维费用背包问题 问题描述: 解决方法: 方法一: 代码实现: 方法二: 代码实现: 背包问题第五讲——二维费用背包问题 背包问题是一类经典的组合优化问题,通常涉及在限定容量的背包中…...
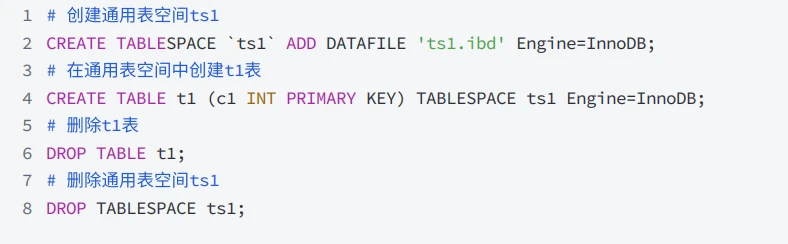
【mysql进阶】4-7. 通用表空间
通⽤表空间 - General Tablespace 1 通⽤表空间的作⽤和特性? ✅ 解答问题 通⽤表空间是使⽤ CREATE tablespace 语法创建的共享InnoDB表空间 通⽤表空间能够存储多个表的数据,与系统表空间类似也是共享表空间; 服务器运⾏时会把表空间元数…...

2024 年互联网大厂 1300 多道 JAVA 面试题汇总,包含了程序员的所有技术点
作为一个 Java 程序员,你平时总是陷在业务开发里,每天噼里啪啦忙敲着代码,上到系统开发,下到 Bug 修改,你感觉自己无所不能。然而偶尔的一次聚会,你听说和自己一起出道的同学早已经年薪 50 万,而…...

【开源免费】基于SpringBoot+Vue.JS在线文档管理系统(JAVA毕业设计)
本文项目编号 T 038 ,文末自助获取源码 \color{red}{T038,文末自助获取源码} T038,文末自助获取源码 目录 一、系统介绍二、演示录屏三、启动教程四、功能截图五、文案资料5.1 选题背景5.2 国内外研究现状5.3 可行性分析 六、核心代码6.1 查…...

Linux资源与网络请求
参数说明: d : 改变显示的更新速度,或是在交谈式指令列( interactive command)按 sq : 没有任何延迟的显示速度,如果使用者是有 superuser 的权限,则 top 将会以最高的优先序执行c : 切换显示模式,共有两种模式&#…...

RPA技术重塑企业自动化的未来
1. RPA定义与原理 1.1 机器人流程自动化(RPA)概念 机器人流程自动化(Robotic Process Automation,简称RPA)是一种软件技术,通过模拟人类用户在计算机界面上的操作来执行重复性的业务流程任务。RPA软件机器人能够自动执行基于规则…...

使用RabbitMQ实现延迟消息的完整指南
在分布式系统中,消息队列通常用于解耦服务,RabbitMQ是一个广泛使用的消息队列服务。延迟消息(也称为延时队列或TTL消息)是一种常见的场景应用,特别适合处理某些任务在一段时间后执行的需求,如订单超时处理、…...
阿里员工:阿里工作7年至少得P7吧,快的都P8了,年薪100W是正常的,80才算及格...
上一篇:一线体面男的收入 年薪64W的阿里蚂蚁员工爆料:在阿里,工作7年至少得P7,快的都P8了,年薪100W才正常,80分才算及格。 其实,在大厂工作,听起来风光无限,但个中滋味&a…...
)
Django进一步掌握(10月22日)
一、请求响应对象 请求对象request 响应对象HttpResponse 二、HttpResponse常用属性 status设置HTTP响应状态码 status_code查询HTTP响应状态码 content_type设置响应的类型 write()写入响应内容 三、重定向 1、实现URl访问的重定向 (1)使用Ht…...

C++从入门到起飞之——红黑树封装map和set 全方位剖析!
目录 1、map和set的整体框架 2、map和set迭代器的实现 3、map支持[] 4、完整源码 set.h map.h RBTree.h 1、map和set的整体框架 因为map和set的底层都是红黑树,所以我们考虑用一个红黑树的类模版去实例化map和set对象!不过,map节点中存…...

【javax maven项目缺少_Maven的依赖管理 引入依赖】
javax maven项目缺少_Maven的依赖管理 引入依赖 Maven的依赖管理 - 引入依赖依赖管理(引入依赖)导入依赖 https://blog.csdn.net/weixin_28932089/article/details/112381468 Maven的依赖管理 - 引入依赖 依赖管理(引入依赖) 能够掌握依赖引入的配置方式 导入依赖 导入依赖练…...

手搓一个定时器
目录 1.什么是定时器 2.计时器的使用 3.手搓定时器 3.1定义一个TimerTask类 3.2定义一个Timer类 3.3实现schedule方法 3.4实现Timer的构造方法 3.4.1随时随地查看优先级队列中是否有任务要执行 3.4.2获取队首任务,并判断是否到执行时间 3.4.3到达执行时间…...

AI提示词工程优化Prompt-GPT使用手册(科普一键收藏史上最强攻略)
Prompt(提示),最初是 NLP 研究者为下游任务设计出来的一种任务专属的输入形式或模板。在 ChatGPT 引发大语言模型新时代之后,Prompt 指与大模型交互输入的代称。 随着大模型的进展,Prompt Engineering是一个持久的探索过程。 目录 什么是提示…...

【数据结构】快速排序(三种实现方式)
目录 一、基本思想 二、动图演示(hoare版) 三、思路分析(图文) 四、代码实现(hoare版) 五、易错提醒 六、相遇场景分析 6.1 ❥ 相遇位置一定比key要小的原因 6.2 ❥ 右边为key,左边先走 …...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

JDK 17 新特性
#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持,不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的ÿ…...

Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决
Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决 问题背景 在一个基于 Spring Cloud Gateway WebFlux 构建的微服务项目中,新增了一个本地验证码接口 /code,使用函数式路由(RouterFunction)和 Hutool 的 Circle…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...

回溯算法学习
一、电话号码的字母组合 import java.util.ArrayList; import java.util.List;import javax.management.loading.PrivateClassLoader;public class letterCombinations {private static final String[] KEYPAD {"", //0"", //1"abc", //2"…...
