背包九讲——二维费用背包问题
目录
二维费用背包问题
问题描述:
解决方法:
方法一:
代码实现:
方法二:
代码实现:
背包问题第五讲——二维费用背包问题
背包问题是一类经典的组合优化问题,通常涉及在限定容量的背包中选择物品,以最大化某种价值或利益。问题的一般描述是:有一个背包,其容量为C;有一组物品,每个物品有重量w和价值v。目标是选择一些物品放入背包,使得它们的总重量不超过背包容量,同时总价值最大。
二维费用背包问题则是背包问题的变体,在背包问题中它只限定物品的重量,二维费用背包会再限定一个维度(体积),在既满足背包容量和既满足背包体积的情况下,使价值最大化。

二维费用背包问题
二维费用背包问题是一种组合优化问题,它是经典的背包问题的扩展。在这个问题中,每件物品具有两个不同的属性,通常被称为“费用”或“资源限制”,以及一个价值。问题的目标是在给定的两种资源限制下,选择一组物品,使得它们的总价值最大。
二维费用背包呢,博主觉得是二重01背包的进化体,之前我们讨论的都是只有一个限定背包容量,比如在背包容量为V所能获得的价值,现在二维费用背包就是又加上了重量(第二维),比如背包容量为V且背包重量不能超过为M所能获得的价值。

问题描述:
- 有一组物品,每件物品都有一个重量(或体积)w[i]和价值v[i]。
- 有两种资源的限制,分别用W和U表示,对应于背包的承重和空间限制。
- 每件物品除了有一个重量w[i],还有一个额外的属性u[i],表示它占用的第二种资源的量。
- 背包可以选择装入或者不装入每件物品,但每件物品只能选择一次。
- 问题的目标是确定应该选择哪些物品,以便在不超过背包的重量W和第二种资源限制U的情况下,使得背包中物品的总价值最大。
题目可以参考一下这个:8. 二维费用的背包问题 - AcWing题库
题目描述基本跟01背包没有什么区别,无非就是多了一个限定条件,我们要在满足此两个条件的基础上去求最大价值。01背包问题之前dp只是定义了一个维度解决一个限定条件的问题,那么我们可以再去扩展一维,那么就可以解决两个限定条件了,我们会发现,这样的动态规划们还可以优化一个维度,这两个方法分别对应下面两个方法。
解决方法:
方法一:
数学上,我们可以使用动态规划来解决这个问题。由于我们是二维的背包,那么定义一个三维数组dp[i][j][k],其中i表示考虑到第i件物品,j表示当前背包的重量不超过j,k表示当前背包的第二种资源不超过k。dp[i][j][k]的值表示在这些条件下的最大价值。
状态转移方程如下:
dp[i][j][k] = max(dp[i-1][j][k], dp[i-1][j-w[i]][k-u[i]] + v[i]) if j >= w[i] && k >= u[i]
其中,dp[i-1][j][k]表示不选择第i件物品时的最大价值,而dp[i-1][j-w[i]][k-u[i]] + v[i]表示选择第i件物品时的最大价值。
最终,问题的解是dp[N][W][U],其中N是物品的总数。

代码实现:
// 遍历所有物品for (int i = 1; i <= n; i++) {for (int j = 0; j <= W; j++) {for (int k = 0; k <= U; k++) {if (j >= weights[i - 1] && k >= volumes[i - 1]) {// 状态转移方程:选或不选第i件物品dp[i][j][k] = max(dp[i - 1][j][k], dp[i - 1][j - weights[i - 1]][k - volumes[i - 1]] + values[i - 1]);} else {// 如果背包无法容纳当前物品,则不选择该物品dp[i][j][k] = dp[i - 1][j][k];}}}}// 返回背包能够容纳的最大价值return dp[n][W][U];方法二:
根据上面的代码,我们可以看出来第一个for循环是有生存周期的,第i个状态只与第i-1个状态有关,所有的第i个状态都是从第i-1个状态转移过来的,与前i-2个状态无关,那么我们可以利用这一点,去滚动数组,此时第i个状态更新便可以从前面的状态转移过来,从而覆盖掉上一个状态的答案,以此类推。这样我们便可以优化掉第一维度,减少了空间复杂度。其实二维费用背包没有什么特别说的,就是01背包的推广,所谓道生一,一生二,二生三,三生万物。既然有二维费用背包,那是不是就有三维、四维……,那么我们可以根据01背包的写法进行改进。

代码实现:
#include<iostream>
using namespace std;
int N,V,M;
int v[1005],m[1005],w[1005],dp[1005][1005];
//dp[i][j]表示体积为i重量为j的情况下所获得最大价值
int main(){cin>>N>>V>>M;//N个物品V背包体积M背包所承受最大重量for(int i=1;i<=N;i++){cin>>v[i]>>m[i]>>w[i];for(int j=V;j>=v[i];j--){for(int k=M;k>=m[i];k--){//这里按照01背包一维优化分两个for来写dp[j][k]=max(dp[j][k],dp[j-v[i]][k-m[i]]+w[i]);//要么选第i个物品要么就不选}}}cout<<dp[V][M]<<endl;return 0;
}上一篇文章:背包九讲——混合背包问题-CSDN博客
背包问题是经典之经典,每一位算法入门学者必学的内容,里面的优化涉及到的也非常具有思维性,值得大家好好学习。由于笔者水平有限,一些方面可能也存在着问题,望大家理解支持,有错误就指出改正,大家一起进步,执笔至此,感触彼多,全文将至,落笔为终,感谢各位的支持,下篇更新分组背包问题。
相关文章:

背包九讲——二维费用背包问题
目录 二维费用背包问题 问题描述: 解决方法: 方法一: 代码实现: 方法二: 代码实现: 背包问题第五讲——二维费用背包问题 背包问题是一类经典的组合优化问题,通常涉及在限定容量的背包中…...
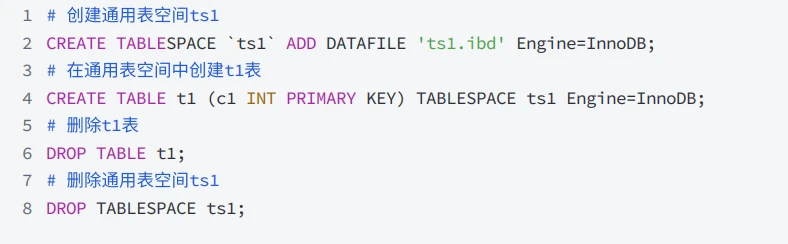
【mysql进阶】4-7. 通用表空间
通⽤表空间 - General Tablespace 1 通⽤表空间的作⽤和特性? ✅ 解答问题 通⽤表空间是使⽤ CREATE tablespace 语法创建的共享InnoDB表空间 通⽤表空间能够存储多个表的数据,与系统表空间类似也是共享表空间; 服务器运⾏时会把表空间元数…...

2024 年互联网大厂 1300 多道 JAVA 面试题汇总,包含了程序员的所有技术点
作为一个 Java 程序员,你平时总是陷在业务开发里,每天噼里啪啦忙敲着代码,上到系统开发,下到 Bug 修改,你感觉自己无所不能。然而偶尔的一次聚会,你听说和自己一起出道的同学早已经年薪 50 万,而…...

【开源免费】基于SpringBoot+Vue.JS在线文档管理系统(JAVA毕业设计)
本文项目编号 T 038 ,文末自助获取源码 \color{red}{T038,文末自助获取源码} T038,文末自助获取源码 目录 一、系统介绍二、演示录屏三、启动教程四、功能截图五、文案资料5.1 选题背景5.2 国内外研究现状5.3 可行性分析 六、核心代码6.1 查…...

Linux资源与网络请求
参数说明: d : 改变显示的更新速度,或是在交谈式指令列( interactive command)按 sq : 没有任何延迟的显示速度,如果使用者是有 superuser 的权限,则 top 将会以最高的优先序执行c : 切换显示模式,共有两种模式&#…...

RPA技术重塑企业自动化的未来
1. RPA定义与原理 1.1 机器人流程自动化(RPA)概念 机器人流程自动化(Robotic Process Automation,简称RPA)是一种软件技术,通过模拟人类用户在计算机界面上的操作来执行重复性的业务流程任务。RPA软件机器人能够自动执行基于规则…...

使用RabbitMQ实现延迟消息的完整指南
在分布式系统中,消息队列通常用于解耦服务,RabbitMQ是一个广泛使用的消息队列服务。延迟消息(也称为延时队列或TTL消息)是一种常见的场景应用,特别适合处理某些任务在一段时间后执行的需求,如订单超时处理、…...
阿里员工:阿里工作7年至少得P7吧,快的都P8了,年薪100W是正常的,80才算及格...
上一篇:一线体面男的收入 年薪64W的阿里蚂蚁员工爆料:在阿里,工作7年至少得P7,快的都P8了,年薪100W才正常,80分才算及格。 其实,在大厂工作,听起来风光无限,但个中滋味&a…...
)
Django进一步掌握(10月22日)
一、请求响应对象 请求对象request 响应对象HttpResponse 二、HttpResponse常用属性 status设置HTTP响应状态码 status_code查询HTTP响应状态码 content_type设置响应的类型 write()写入响应内容 三、重定向 1、实现URl访问的重定向 (1)使用Ht…...

C++从入门到起飞之——红黑树封装map和set 全方位剖析!
目录 1、map和set的整体框架 2、map和set迭代器的实现 3、map支持[] 4、完整源码 set.h map.h RBTree.h 1、map和set的整体框架 因为map和set的底层都是红黑树,所以我们考虑用一个红黑树的类模版去实例化map和set对象!不过,map节点中存…...

【javax maven项目缺少_Maven的依赖管理 引入依赖】
javax maven项目缺少_Maven的依赖管理 引入依赖 Maven的依赖管理 - 引入依赖依赖管理(引入依赖)导入依赖 https://blog.csdn.net/weixin_28932089/article/details/112381468 Maven的依赖管理 - 引入依赖 依赖管理(引入依赖) 能够掌握依赖引入的配置方式 导入依赖 导入依赖练…...

手搓一个定时器
目录 1.什么是定时器 2.计时器的使用 3.手搓定时器 3.1定义一个TimerTask类 3.2定义一个Timer类 3.3实现schedule方法 3.4实现Timer的构造方法 3.4.1随时随地查看优先级队列中是否有任务要执行 3.4.2获取队首任务,并判断是否到执行时间 3.4.3到达执行时间…...

AI提示词工程优化Prompt-GPT使用手册(科普一键收藏史上最强攻略)
Prompt(提示),最初是 NLP 研究者为下游任务设计出来的一种任务专属的输入形式或模板。在 ChatGPT 引发大语言模型新时代之后,Prompt 指与大模型交互输入的代称。 随着大模型的进展,Prompt Engineering是一个持久的探索过程。 目录 什么是提示…...

【数据结构】快速排序(三种实现方式)
目录 一、基本思想 二、动图演示(hoare版) 三、思路分析(图文) 四、代码实现(hoare版) 五、易错提醒 六、相遇场景分析 6.1 ❥ 相遇位置一定比key要小的原因 6.2 ❥ 右边为key,左边先走 …...
)
利用前向勾子获取神经网络中间层的输出并将其进行保存(示例详解)
代码示例: # 激活字典,用于保存每次的中间特征 activation {}# 将 forward_hook 函数定义在 upsample_v2 外部 def forward_hook(name):def hook(module, input, output):activation[name] output.detach()return hookdef upsample_v2(in_channels, o…...

CTF-RE 从0到N: S盒
S盒(Substitution Box) 是密码学中的一种替换表,用于对输入数据进行非线性变换,以增加加密过程的复杂性。它主要用于对称加密算法中(例如AES、DES),作为加密轮次的一部分,对输入字节…...
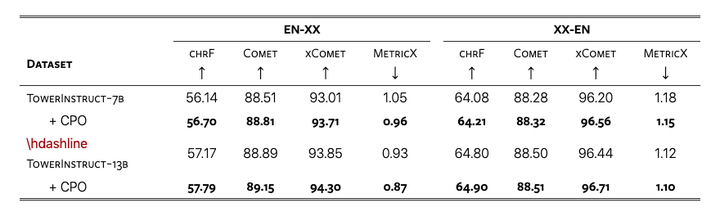
MT-Pref数据集:包含18种语言的18k实例,涵盖多个领域。实验表明它能有效提升Tower模型在WMT23和FLORES基准测试中的翻译质量。
2024-10-10,由电信研究所、里斯本大学等联合创建MT-Pref数据集,它包含18种语言方向的18k实例,覆盖了2022年后的多个领域文本。通过在WMT23和FLORES基准测试上的实验,我们展示了使用MT-Pref数据集对Tower模型进行对齐可以显著提高翻…...

【C++ 真题】B2099 矩阵交换行
矩阵交换行 题目描述 给定一个 5 5 5 \times 5 55 的矩阵(数学上,一个 r c r \times c rc 的矩阵是一个由 r r r 行 c c c 列元素排列成的矩形阵列),将第 n n n 行和第 m m m 行交换,输出交换后的结果。 输入格式 输入共 6 6 6 …...
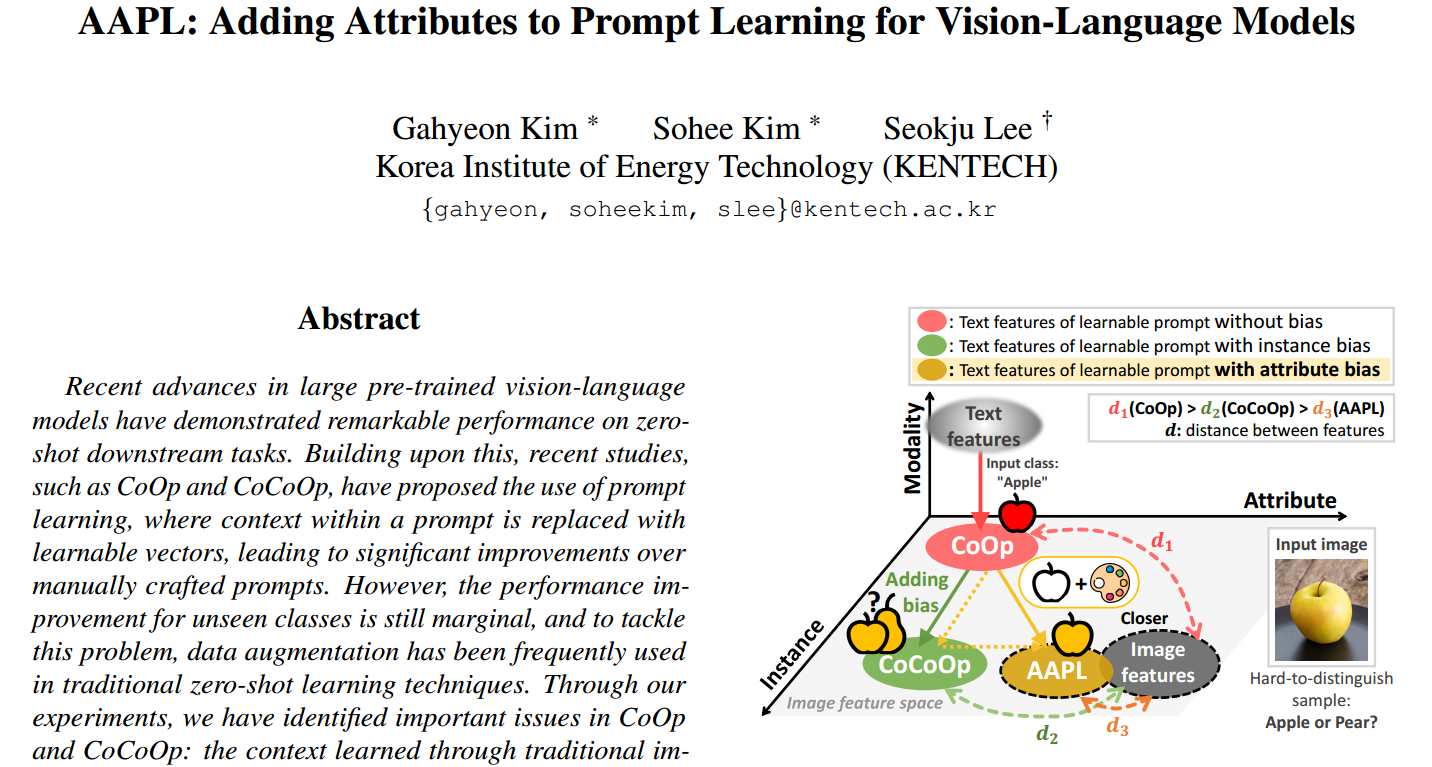
AAPL: Adding Attributes to Prompt Learning for Vision-Language Models
文章汇总 当前的问题 1.元标记未能捕获分类的关键语义特征 如下图(a)所示, π \pi π在类聚类方面没有显示出很大的差异,这表明元标记 π \pi π未能捕获分类的关键语义特征。我们进行简单的数据增强后,如图(b)所示,效果也是如…...
)
MySQLDBA修炼之道-开发篇(一)
三、开发基础 1. 数据模型 1.1 关系数据模型介绍 关于NULL 如果某个字段的值是未知的或未定义的,数据库会提供一个特殊的值NULL来表示。NULL值很特殊,在关系数据库中应该小心处理。例如查询语句“select*from employee where 绩效得分<85 or>绩…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...

AI病理诊断七剑下天山,医疗未来触手可及
一、病理诊断困局:刀尖上的医学艺术 1.1 金标准背后的隐痛 病理诊断被誉为"诊断的诊断",医生需通过显微镜观察组织切片,在细胞迷宫中捕捉癌变信号。某省病理质控报告显示,基层医院误诊率达12%-15%,专家会诊…...

论文阅读笔记——Muffin: Testing Deep Learning Libraries via Neural Architecture Fuzzing
Muffin 论文 现有方法 CRADLE 和 LEMON,依赖模型推理阶段输出进行差分测试,但在训练阶段是不可行的,因为训练阶段直到最后才有固定输出,中间过程是不断变化的。API 库覆盖低,因为各个 API 都是在各种具体场景下使用。…...

关于easyexcel动态下拉选问题处理
前些日子突然碰到一个问题,说是客户的导入文件模版想支持部分导入内容的下拉选,于是我就找了easyexcel官网寻找解决方案,并没有找到合适的方案,没办法只能自己动手并分享出来,针对Java生成Excel下拉菜单时因选项过多导…...

Kubernetes 节点自动伸缩(Cluster Autoscaler)原理与实践
在 Kubernetes 集群中,如何在保障应用高可用的同时有效地管理资源,一直是运维人员和开发者关注的重点。随着微服务架构的普及,集群内各个服务的负载波动日趋明显,传统的手动扩缩容方式已无法满足实时性和弹性需求。 Cluster Auto…...

加密通信 + 行为分析:运营商行业安全防御体系重构
在数字经济蓬勃发展的时代,运营商作为信息通信网络的核心枢纽,承载着海量用户数据与关键业务传输,其安全防御体系的可靠性直接关乎国家安全、社会稳定与企业发展。随着网络攻击手段的不断升级,传统安全防护体系逐渐暴露出局限性&a…...
