C++从入门到起飞之——红黑树封装map和set 全方位剖析!
目录
1、map和set的整体框架
2、map和set迭代器的实现
3、map支持[]
4、完整源码
set.h
map.h
RBTree.h
1、map和set的整体框架
因为map和set的底层都是红黑树,所以我们考虑用一个红黑树的类模版去实例化map和set对象!不过,map节点中存储的是一个pair对象,而set中存储的是一个key对象。所以我们第一步就是先调整一下我们之前实现的红黑树的节点结构。
//节点结构(不知道存储pair类型的key/val结构还是Key结构)
template<class T>
struct RBTreeNode
{RBTreeNode(const T& data):_data(data), _parent(nullptr), _left(nullptr), _right(nullptr), _col(RED){}T _data;RBTreeNode* _parent;RBTreeNode* _left;RBTreeNode* _right;Colour _col;//初始化为红色
};无论是set还是map的查找都是根据key来进行的,所以我们的红黑树类模版的第一个参数类型是接受上层传递过来的K类型。
再有,set和map的insert(插入),一个是pair类型,一个是key类型。所以我们的红黑树类模版的第二个参数类型是接受上层传递过来的T类型。
最后,我们还要在上层传递一个仿函数用于底层红黑树查找和插入删除时用key比较。因为set直接插入一个key可以用于比较,但是map插入一个pair,而pair支持的比较是first和second一起比较,而我们只希望用key比较。又因为底层并不知道上层是set还是map,所以我们要在上层传递一个仿函数给到下层让下层用上层的仿函数拿到key来比较大小!
set整体框架:
namespace my_set
{template<class K>class set{//仿函数用于底层红黑树查找和插入删除时用key比较struct SetKeyOfT{const K& operator()(const K& key){return key;}};public:bool insert(const K& key){return _t.insert(key);}private:RBTree<K, K, SetKeyOfT> _t;};
}map整体框架:
namespace my_map
{template<class K,class V>class map{/*仿函数用于底层红黑树查找和插入删除时用key比较因为set直接插入一个key可以用于比较,但是map插入一个pair,而pair支持的比较是first和second一起比较,而我们只希望用key比较又底层并不知道上层是set还是map,所以我们要在上层传递一个仿函数给到下层让下层用上层的仿函数拿到key来比较大小!*/struct MapKeyOfT{const K& operator()(const pair<K,V>& kv){return kv.first;}};public:bool insert(const pair<K,V>& kv){return _t.insert(kv);}private:RBTree<K, pair<K,V>, MapKeyOfT> _t;};
}调整过后的底层红黑树:
//枚举类型定义颜色
enum Colour
{RED,BLACK
};
//节点结构(不知道存储pair类型的key/val结构还是Key结构)
template<class T>
struct RBTreeNode
{RBTreeNode(const T& data):_data(data), _parent(nullptr), _left(nullptr), _right(nullptr), _col(RED){}T _data;RBTreeNode* _parent;RBTreeNode* _left;RBTreeNode* _right;Colour _col;//初始化为红色
};//红黑树
template<class K, class T,class KeyOfT>
class RBTree
{typedef RBTreeNode<T> Node;
public:KeyOfT kot;//默认构造RBTree() = default;//拷贝构造RBTree(const T& rbt){_root = _copy(rbt._root);}// 赋值重载RBTree<K, T,KeyOfT>& operator=(T tmp){std::swap(_root, tmp._root);return *this;}//二叉树的析构~RBTree(){_Destroy(_root);}//红黑树的查找Node* Find(const K& key){Node* cur = _root;while (cur){if (kot(cur->_data) < kot(key)){cur = cur->_right;}else if (kot(cur->_data) > kot(key)){cur = cur->_left;}else{return cur;}}return nullptr;}//红黑树的插入bool insert(const T& data){//如果树为空,在根插入并且颜色为黑色if (_root == nullptr){_root = new Node(data);_root->_col = BLACK;return true;}//树不为空按搜索树规则先进行插入Node* parent = nullptr;Node* cur = _root;while (cur){if (kot(data) < kot(cur->_data))//小往左走{parent = cur;cur = parent->_left;}else if (kot(data) > kot(cur->_data))//大往右走{parent = cur;cur = parent->_right;}else{return false;//不支持相同元素的插入}}cur = new Node(data);cur->_col = RED;if (kot(data) < kot(parent->_data))//K小插入在左边parent->_left = cur;else//K大插入在右边parent->_right = cur;cur->_parent = parent;//插入后进行维护红黑树规则的逻辑//parent存在且为红while (parent && parent->_col == RED){Node* grandfather = parent->_parent;//p在g的右边if (parent == grandfather->_right){//g//u pNode* uncle = grandfather->_left;if (uncle && uncle->_col == RED)//uncle存在且为红{//变色处理uncle->_col = parent->_col = BLACK;grandfather->_col = RED;//更新cur继续向上处理cur = grandfather;parent = cur->_parent;}else//uncle不存在或者存在且为黑{if (cur == parent->_right){//g//u p// c//以g为旋转点进行左单旋RotateL(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else{//g//u p// c//进行右左双旋RotateR(parent);RotateL(grandfather);cur->_col = BLACK;grandfather->_col = RED;}//旋转+变色后链接祖先节点的节点为黑,必然不会发生连续红色节点的情况直接break;break;}}else//p在g的左边{//g//p uNode* uncle = grandfather->_right;if (uncle && uncle->_col == RED)//uncle存在且为红{//变色处理uncle->_col = parent->_col = BLACK;grandfather->_col = RED;//更新cur继续向上处理cur = grandfather;parent = cur->_parent;}else//uncle不存在或者存在且为黑{if (cur == parent->_left){//g//p u//c//以g为旋转点进行右单旋RotateR(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else{//g//p u// c//进行左右双旋RotateL(parent);RotateR(grandfather);cur->_col = BLACK;grandfather->_col = RED;}//旋转+变色后链接祖先节点的节点为黑,必然不会发生连续红色节点的情况直接break;break;}}}//如果持续更新变色到根_root->_col = BLACK;return true;}private://右单旋void RotateR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;Node* pParent = parent->_parent;parent->_left = subLR;if (subLR)//如果不为空subLR->_parent = parent;subL->_right = parent;parent->_parent = subL;if (pParent == nullptr){_root = subL;subL->_parent = nullptr;}else{if (pParent->_left == parent){pParent->_left = subL;}else{pParent->_right = subL;}subL->_parent = pParent;}}//左单旋void RotateL(Node* parent){Node* pParent = parent->_parent;Node* subR = parent->_right;Node* subRL = subR->_left;subR->_left = parent;parent->_parent = subR;parent->_right = subRL;if (subRL)subRL->_parent = parent;if (pParent == nullptr){_root = subR;subR->_parent = nullptr;}else{if (pParent->_left == parent){pParent->_left = subR;}else{pParent->_right = subR;}subR->_parent = pParent;}}//递归拷贝Node* _copy(Node* root){if (root == nullptr)return nullptr;Node* newNode = new Node(root->_data);newNode->_left = _copy(root->_left);newNode->_right = _copy(root->_right);return newNode;}//二叉树的销毁void _Destroy(Node* root){if (root == nullptr)return;_Destroy(root->_left);_Destroy(root->_right);delete root;}private:Node* _root = nullptr;
};2、map和set迭代器的实现
map和set迭代器的实现其实思路与list迭代器的实现几乎一样,它们都是由一个一个的节点组成的。所以我们都是通过封装一个节点的指针,重载*、->、++、--、比较等运算符!
迭代器的整体框架:
//封装一个节点指针作为迭代器
template<class T,class Ref,class Ptr>
struct RBTreeIterator
{typedef RBTreeNode<T> Node;typedef RBTreeIterator<T,Ref,Ptr> Self;Node* _node;Node* _root;RBTreeIterator(Node* node,Node* root):_node(node),_root(root){}//迭代器的++Self& operator++(){}//迭代器的--Self& operator--(){}//简单的运算符重载Ref operator*(){return _node->_data;}Ptr operator->(){return &_node->_data;}bool operator!=(const Self& s) const{return _node != s._node;}bool operator==(const Self& s) const{return _node == s._node;}
};map和set迭代器的难点在于++和--:
iterator实现思路分析
• iterator实现的⼤框架跟list的iterator思路是⼀致的,⽤⼀个类型封装结点的指针,再通过重载运算 符实现,迭代器像指针⼀样访问的⾏为。
• 这⾥的难点是operator++和operator--的实现。之前使⽤部分,我们分析了,map和set的迭代器⾛ 的是中序遍历,左⼦树->根结点->右⼦树,那么begin()会返回中序第⼀个结点的iterator也就是10 所在结点的迭代器。
• 迭代器++的核⼼逻辑就是不看全局,只看局部,只考虑当前中序局部要访问的下⼀个结点。
• 迭代器++时,如果it指向的结点的右⼦树不为空,代表当前结点已经访问完了,要访问下⼀个结点 是右⼦树的中序第⼀个,⼀棵树中序第⼀个是最左结点,所以直接找右⼦树的最左结点即可。
• 迭代器++时,如果it指向的结点的右⼦树空,代表当前结点已经访问完了且当前结点所在的⼦树也 访问完了,要访问的下⼀个结点在当前结点的祖先⾥⾯,所以要沿着当前结点到根的祖先路径向上 找。
• 如果当前结点是⽗亲的左,根据中序左⼦树->根结点->右⼦树,那么下⼀个访问的结点就是当前结 点的⽗亲;
如下图:it指向25,25右为空,25是30的左,所以下⼀个访问的结点就是30。
• 如果当前结点是⽗亲的右,根据中序左⼦树->根结点->右⼦树,当前当前结点所在的⼦树访问完 了,当前结点所在⽗亲的⼦树也访问完了,那么下⼀个访问的需要继续往根的祖先中去找,直到找 到孩⼦是⽗亲左的那个祖先就是中序要问题的下⼀个结点。
如下图:it指向15,15右为空,15是10 的右,15所在⼦树话访问完了,10所在⼦树也访问完了,继续往上找,10是18的左,那么下⼀个 访问的结点就是18。
• end()如何表⽰呢?
如下图:当it指向50时,++it时,50是40的右,40是30的右,30是18的右,18 到根没有⽗亲,没有找到孩⼦是⽗亲左的那个祖先,这是⽗亲为空了,那我们就把it中的结点指针 置为nullptr,我们⽤nullptr去充当end。需要注意的是stl源码空,红⿊树增加了⼀个哨兵位头结点 做为end(),这哨兵位头结点和根互为⽗亲,左指向最左结点,右指向最右结点。相⽐我们⽤ nullptr作为end(),差别不⼤,他能实现的,我们也能实现。只是--end()判断到结点时空,特殊处 理⼀下,让迭代器结点指向最右结点。具体参考迭代器--实现。
• 迭代器--的实现跟++的思路完全类似,逻辑正好反过来即可,因为他访问顺序是右⼦树->根结点-> 左⼦树,具体参考下⾯代码实现。
• set的iterator也不⽀持修改,我们把set的第⼆个模板参数改成const K即可, RBTreeconst K, SetKeyOfT> _t;
• map的iterator不⽀持修改key但是可以修改value,我们把map的第⼆个模板参数pair的第⼀个参 数改成const K即可, RBTreepair, MapKeyOfT> _t;
• ⽀持完整的迭代器还有很多细节需要修改,具体参考下⾯题的代码。


迭代器++代码:
//迭代器的++
Self& operator++()
{//如果当前节点的右不为空,那下一个节点就是右子树的最左节点if (_node->_right){Node* leftMost = _node->_right;while (leftMost->_left){leftMost = leftMost->_left;}_node = leftMost;}/*如果当前节点的右为空,则说明当前节点的中序已近完毕如果当前节点是父亲的右,说明父亲的中序也完毕所以我们要找到祖先节点中是父亲的左的那个节点,那下一个节点就是就是父亲*/else{Node* cur = _node;Node* parent = cur->_parent;//父亲不为空并且cur是父亲的右,不断向上寻找while (parent && cur == parent->_right){cur = parent;parent = cur->_parent;}//走到这里父亲为空说明走到end,不为空父亲则是中序的下一个_node = parent;}return *this;
}因为我们用空来代表数的末尾,但我们--时,如果此时迭代器恰好在end()位置,那我们就要单独考虑这种情况。其他逻辑就和++相反!
要找到树的最右节点,那么就还必须知道根节点_root!所以我们在红黑树中构造一个迭代器时,不仅要传递当前位置的节点,还要传根节点!
//迭代器的--
Self& operator--()
{//--后为中序的最右那一个if (_node == nullptr){Node* rightMost = _root;while (rightMost&&rightMost->_right){rightMost = rightMost->_right;}_node = rightMost;}//如果当前节点的左不为空,那下一个节点就是左子树的最右节点else if (_node->_left){Node* rightMost = _node->_left;while (rightMost->_right){rightMost = rightMost->_right;}_node = rightMost;}/*如果当前节点的左为空,则说明当前节点的中序已近完毕如果当前节点是父亲的左,说明父亲的中序也完毕所以我们要找到祖先节点中是父亲的右的那个节点,那下一个节点就是就是父亲*/else{Node* cur = _node;Node* parent = cur->_parent;//父亲不为空并且cur是父亲的左,不断向上寻找while (parent && cur == parent->_left){cur = parent;parent = cur->_parent;}//走到这里父亲为空说明走到end,不为空父亲则是中序的下一个_node = parent;}return *this;
}底层红黑树的begin和end:
typedef RBTreeNode<T> Node;
typedef RBTreeIterator<T, T&, T*> Iterator;
typedef RBTreeIterator<T, const T&, const T*> ConstIterator;
Iterator Begin()
{Node* leftMost = _root;while (leftMost && leftMost->_left){leftMost = leftMost->_left;}return Iterator(leftMost, _root);
}
Iterator End()
{return Iterator(nullptr, _root);
}
ConstIterator CBegin() const
{Node* leftMost = _root;while (leftMost && leftMost->_left){leftMost = leftMost->_left;}return Iterator(leftMost, _root);
}
ConstIterator CEnd() const
{return Iterator(nullptr, _root);
}3、map支持[]
map的[]重载主要是复用了底层红黑树当中的insert接口,insert充当查找和插入的功能!
我们在使用[]时,如果map中有和我们外面传递的key相同的key,那insert就会插入失败并且返回这个key的迭代器。如果不存在,那insert就会插入成功并且返回这个key的迭代器。所以我们要调整一下insert的返回值为pair<iterator,bool>
而map的[]还支持修改(key所映射的val)的功能,insert返回的迭代器在修改val时发挥作用!
V& operator[](const K& key)
{pair<iterator, bool> ret = _t.Insert(make_pair(key, V()));return ret.first->second;
}4、完整源码
set.h
#pragma once
#include"RBTree.h"
namespace my_set
{template<class K>class set{//仿函数用于底层红黑树查找和插入删除时用key比较struct SetKeyOfT{const K& operator()(const K& key){return key;}};public:typedef typename RBTree<K, const K, SetKeyOfT>::Iterator iterator;typedef typename RBTree<K, const K, SetKeyOfT>::ConstIterator const_iterator;iterator begin(){return _t.Begin();}iterator end(){return _t.End();}const_iterator cbegin() const{return _t.CBegin();}const_iterator cend() const{return _t.CEnd();}pair<iterator,bool> insert(const K& key){return _t.Insert(key);}iterator find(const K& key){return _t.Find(key);}private:RBTree<K, const K, SetKeyOfT> _t;};
}map.h
#pragma once
#include"RBTree.h"
namespace my_map
{template<class K,class V>class map{/*仿函数用于底层红黑树查找和插入删除时用key比较因为set直接插入一个key可以用于比较,但是map插入一个pair,而pair支持的比较是first和second一起比较,而我们只希望用key比较又底层并不知道上层是set还是map,所以我们要在上层传递一个仿函数给到下层让下层用上层的仿函数拿到key来比较大小!*/struct MapKeyOfT{const K& operator()(const pair<K,V>& kv){return kv.first;}};public:typedef typename RBTree<K, pair<const K, V>, MapKeyOfT>::Iterator iterator;typedef typename RBTree<K, pair<const K, V>, MapKeyOfT>::ConstIterator const_iterator;iterator begin(){return _t.Begin();}iterator end(){return _t.End();}const_iterator cbegin() const{return _t.CBegin();}const_iterator cend() const{return _t.CEnd();}pair<iterator, bool> insert(const pair<K,V>& kv){return _t.Insert(kv);}iterator find(const K& key){return _t.Find(key);}V& operator[](const K& key){pair<iterator, bool> ret = _t.Insert(make_pair(key, V()));return ret.first->second;}private:RBTree<K, pair<const K,V>, MapKeyOfT> _t;};
}RBTree.h

#pragma once
#include<iostream>
using namespace std;//枚举类型定义颜色
enum Colour
{RED,BLACK
};//节点结构(不知道存储pair类型的key/val结构还是Key结构)
template<class T>
struct RBTreeNode
{RBTreeNode(const T& data):_data(data), _parent(nullptr), _left(nullptr), _right(nullptr), _col(RED){}T _data;RBTreeNode* _parent;RBTreeNode* _left;RBTreeNode* _right;Colour _col;//初始化为红色
};//封装一个节点指针作为迭代器
template<class T,class Ref,class Ptr>
struct RBTreeIterator
{typedef RBTreeNode<T> Node;typedef RBTreeIterator<T,Ref,Ptr> Self;Node* _node;Node* _root;RBTreeIterator(Node* node,Node* root):_node(node),_root(root){}//迭代器的++Self& operator++(){//如果当前节点的右不为空,那下一个节点就是右子树的最左节点if (_node->_right){Node* leftMost = _node->_right;while (leftMost->_left){leftMost = leftMost->_left;}_node = leftMost;}/*如果当前节点的右为空,则说明当前节点的中序已近完毕如果当前节点是父亲的右,说明父亲的中序也完毕所以我们要找到祖先节点中是父亲的左的那个节点,那下一个节点就是就是父亲*/else{Node* cur = _node;Node* parent = cur->_parent;//父亲不为空并且cur是父亲的右,不断向上寻找while (parent && cur == parent->_right){cur = parent;parent = cur->_parent;}//走到这里父亲为空说明走到end,不为空父亲则是中序的下一个_node = parent;}return *this;}//迭代器的--Self& operator--(){//--后为中序的最右那一个if (_node == nullptr){Node* rightMost = _root;while (rightMost&&rightMost->_right){rightMost = rightMost->_right;}_node = rightMost;}//如果当前节点的左不为空,那下一个节点就是左子树的最右节点else if (_node->_left){Node* rightMost = _node->_left;while (rightMost->_right){rightMost = rightMost->_right;}_node = rightMost;}/*如果当前节点的左为空,则说明当前节点的中序已近完毕如果当前节点是父亲的左,说明父亲的中序也完毕所以我们要找到祖先节点中是父亲的右的那个节点,那下一个节点就是就是父亲*/else{Node* cur = _node;Node* parent = cur->_parent;//父亲不为空并且cur是父亲的左,不断向上寻找while (parent && cur == parent->_left){cur = parent;parent = cur->_parent;}//走到这里父亲为空说明走到end,不为空父亲则是中序的下一个_node = parent;}return *this;}//简单的运算符重载Ref operator*(){return _node->_data;}Ptr operator->(){return &_node->_data;}bool operator!=(const Self& s) const{return _node != s._node;}bool operator==(const Self& s) const{return _node == s._node;}
};//红黑树
template<class K, class T,class KeyOfT>
class RBTree
{
public:typedef RBTreeNode<T> Node;typedef RBTreeIterator<T, T&, T*> Iterator;typedef RBTreeIterator<T, const T&, const T*> ConstIterator;Iterator Begin(){Node* leftMost = _root;while (leftMost && leftMost->_left){leftMost = leftMost->_left;}return Iterator(leftMost, _root);}Iterator End(){return Iterator(nullptr, _root);}ConstIterator CBegin() const{Node* leftMost = _root;while (leftMost && leftMost->_left){leftMost = leftMost->_left;}return Iterator(leftMost, _root);}ConstIterator CEnd() const{return Iterator(nullptr, _root);}KeyOfT kot;//默认构造RBTree() = default;//拷贝构造RBTree(const T& rbt){_root = _copy(rbt._root);}// 赋值重载RBTree<K, T,KeyOfT>& operator=(T tmp){std::swap(_root, tmp._root);return *this;}//二叉树的析构~RBTree(){_Destroy(_root);}//红黑树的查找Node* Find(const K& key){Node* cur = _root;while (cur){if (kot(cur->_data) < kot(key)){cur = cur->_right;}else if (kot(cur->_data) > kot(key)){cur = cur->_left;}else{return Iterator(cur,_root);}}return End();}//红黑树的插入pair<Iterator,bool> Insert(const T& data){//如果树为空,在根插入并且颜色为黑色if (_root == nullptr){_root = new Node(data);_root->_col = BLACK;return make_pair(Iterator(_root,_root),true);}//树不为空按搜索树规则先进行插入Node* parent = nullptr;Node* cur = _root;while (cur){if (kot(data) < kot(cur->_data))//小往左走{parent = cur;cur = parent->_left;}else if (kot(data) > kot(cur->_data))//大往右走{parent = cur;cur = parent->_right;}else{return make_pair(Iterator(cur, _root), false);//不支持相同元素的插入}}cur = new Node(data);Node* newnode = cur;cur->_col = RED;if (kot(data) < kot(parent->_data))//K小插入在左边parent->_left = cur;else//K大插入在右边parent->_right = cur;cur->_parent = parent;//插入后进行维护红黑树规则的逻辑//parent存在且为红while (parent && parent->_col == RED){Node* grandfather = parent->_parent;//p在g的右边if (parent == grandfather->_right){//g//u pNode* uncle = grandfather->_left;if (uncle && uncle->_col == RED)//uncle存在且为红{//变色处理uncle->_col = parent->_col = BLACK;grandfather->_col = RED;//更新cur继续向上处理cur = grandfather;parent = cur->_parent;}else//uncle不存在或者存在且为黑{if (cur == parent->_right){//g//u p// c//以g为旋转点进行左单旋RotateL(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else{//g//u p// c//进行右左双旋RotateR(parent);RotateL(grandfather);cur->_col = BLACK;grandfather->_col = RED;}//旋转+变色后链接祖先节点的节点为黑,必然不会发生连续红色节点的情况直接break;break;}}else//p在g的左边{//g//p uNode* uncle = grandfather->_right;if (uncle && uncle->_col == RED)//uncle存在且为红{//变色处理uncle->_col = parent->_col = BLACK;grandfather->_col = RED;//更新cur继续向上处理cur = grandfather;parent = cur->_parent;}else//uncle不存在或者存在且为黑{if (cur == parent->_left){//g//p u//c//以g为旋转点进行右单旋RotateR(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else{//g//p u// c//进行左右双旋RotateL(parent);RotateR(grandfather);cur->_col = BLACK;grandfather->_col = RED;}//旋转+变色后链接祖先节点的节点为黑,必然不会发生连续红色节点的情况直接break;break;}}}//如果持续更新变色到根_root->_col = BLACK;return make_pair(Iterator(newnode, _root), true);}private://右单旋void RotateR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;Node* pParent = parent->_parent;parent->_left = subLR;if (subLR)//如果不为空subLR->_parent = parent;subL->_right = parent;parent->_parent = subL;if (pParent == nullptr){_root = subL;subL->_parent = nullptr;}else{if (pParent->_left == parent){pParent->_left = subL;}else{pParent->_right = subL;}subL->_parent = pParent;}}//左单旋void RotateL(Node* parent){Node* pParent = parent->_parent;Node* subR = parent->_right;Node* subRL = subR->_left;subR->_left = parent;parent->_parent = subR;parent->_right = subRL;if (subRL)subRL->_parent = parent;if (pParent == nullptr){_root = subR;subR->_parent = nullptr;}else{if (pParent->_left == parent){pParent->_left = subR;}else{pParent->_right = subR;}subR->_parent = pParent;}}//递归拷贝Node* _copy(Node* root){if (root == nullptr)return nullptr;Node* newNode = new Node(root->_data);newNode->_left = _copy(root->_left);newNode->_right = _copy(root->_right);return newNode;}//二叉树的销毁void _Destroy(Node* root){if (root == nullptr)return;_Destroy(root->_left);_Destroy(root->_right);delete root;}
private:Node* _root = nullptr;
};
相关文章:

C++从入门到起飞之——红黑树封装map和set 全方位剖析!
目录 1、map和set的整体框架 2、map和set迭代器的实现 3、map支持[] 4、完整源码 set.h map.h RBTree.h 1、map和set的整体框架 因为map和set的底层都是红黑树,所以我们考虑用一个红黑树的类模版去实例化map和set对象!不过,map节点中存…...

【javax maven项目缺少_Maven的依赖管理 引入依赖】
javax maven项目缺少_Maven的依赖管理 引入依赖 Maven的依赖管理 - 引入依赖依赖管理(引入依赖)导入依赖 https://blog.csdn.net/weixin_28932089/article/details/112381468 Maven的依赖管理 - 引入依赖 依赖管理(引入依赖) 能够掌握依赖引入的配置方式 导入依赖 导入依赖练…...

手搓一个定时器
目录 1.什么是定时器 2.计时器的使用 3.手搓定时器 3.1定义一个TimerTask类 3.2定义一个Timer类 3.3实现schedule方法 3.4实现Timer的构造方法 3.4.1随时随地查看优先级队列中是否有任务要执行 3.4.2获取队首任务,并判断是否到执行时间 3.4.3到达执行时间…...

AI提示词工程优化Prompt-GPT使用手册(科普一键收藏史上最强攻略)
Prompt(提示),最初是 NLP 研究者为下游任务设计出来的一种任务专属的输入形式或模板。在 ChatGPT 引发大语言模型新时代之后,Prompt 指与大模型交互输入的代称。 随着大模型的进展,Prompt Engineering是一个持久的探索过程。 目录 什么是提示…...

【数据结构】快速排序(三种实现方式)
目录 一、基本思想 二、动图演示(hoare版) 三、思路分析(图文) 四、代码实现(hoare版) 五、易错提醒 六、相遇场景分析 6.1 ❥ 相遇位置一定比key要小的原因 6.2 ❥ 右边为key,左边先走 …...
)
利用前向勾子获取神经网络中间层的输出并将其进行保存(示例详解)
代码示例: # 激活字典,用于保存每次的中间特征 activation {}# 将 forward_hook 函数定义在 upsample_v2 外部 def forward_hook(name):def hook(module, input, output):activation[name] output.detach()return hookdef upsample_v2(in_channels, o…...

CTF-RE 从0到N: S盒
S盒(Substitution Box) 是密码学中的一种替换表,用于对输入数据进行非线性变换,以增加加密过程的复杂性。它主要用于对称加密算法中(例如AES、DES),作为加密轮次的一部分,对输入字节…...
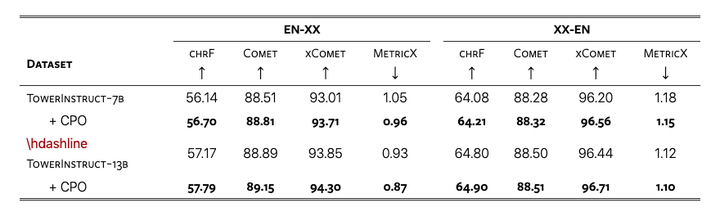
MT-Pref数据集:包含18种语言的18k实例,涵盖多个领域。实验表明它能有效提升Tower模型在WMT23和FLORES基准测试中的翻译质量。
2024-10-10,由电信研究所、里斯本大学等联合创建MT-Pref数据集,它包含18种语言方向的18k实例,覆盖了2022年后的多个领域文本。通过在WMT23和FLORES基准测试上的实验,我们展示了使用MT-Pref数据集对Tower模型进行对齐可以显著提高翻…...

【C++ 真题】B2099 矩阵交换行
矩阵交换行 题目描述 给定一个 5 5 5 \times 5 55 的矩阵(数学上,一个 r c r \times c rc 的矩阵是一个由 r r r 行 c c c 列元素排列成的矩形阵列),将第 n n n 行和第 m m m 行交换,输出交换后的结果。 输入格式 输入共 6 6 6 …...
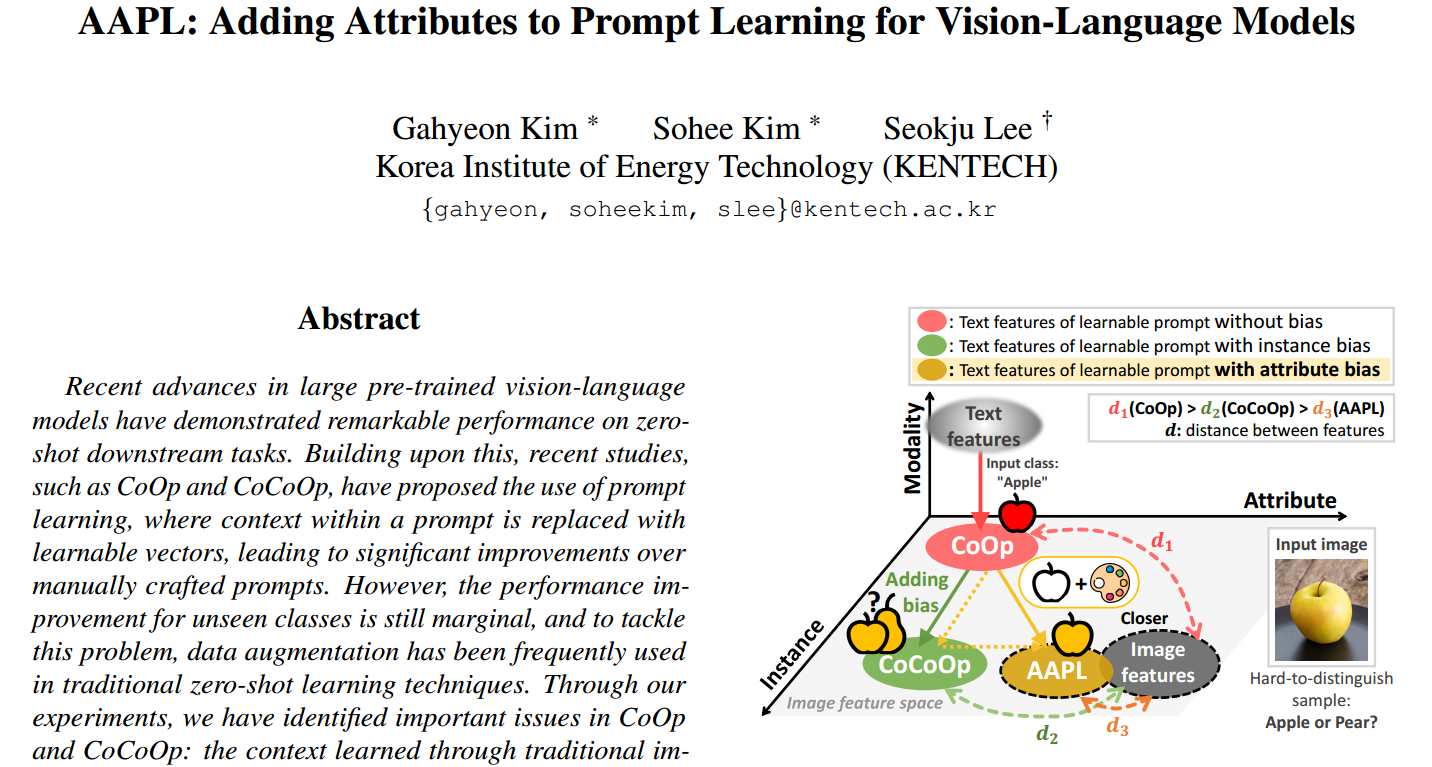
AAPL: Adding Attributes to Prompt Learning for Vision-Language Models
文章汇总 当前的问题 1.元标记未能捕获分类的关键语义特征 如下图(a)所示, π \pi π在类聚类方面没有显示出很大的差异,这表明元标记 π \pi π未能捕获分类的关键语义特征。我们进行简单的数据增强后,如图(b)所示,效果也是如…...
)
MySQLDBA修炼之道-开发篇(一)
三、开发基础 1. 数据模型 1.1 关系数据模型介绍 关于NULL 如果某个字段的值是未知的或未定义的,数据库会提供一个特殊的值NULL来表示。NULL值很特殊,在关系数据库中应该小心处理。例如查询语句“select*from employee where 绩效得分<85 or>绩…...

Spring MVC 知识点全解析
Spring MVC 知识点全解析 Spring MVC 是一个基于 Java 的请求驱动的 Web 框架,属于 Spring 框架的一部分,广泛用于构建企业级 Web 应用程序。本文将详细阐述 Spring MVC 的核心知识点,包括其工作原理、关键组件、配置、请求处理、数据绑定、…...

python 基于FastAPI实现一个简易的在线用户统计 服务
简易在线用户统计服务 概述 这是一个基于Python的FastAPI框架实现的服务,用于统计客户端的心跳信息,并据此维护在线用户列表以及记录活跃用户数。 功能特性 心跳接收:接受来自客户端的心跳包,以更新客户端的状态。在线用户统计…...

glibc中xdr的一个bug
本人在64位linux服务器上(centos7),发现xdr_u_long这个函数有个bug,就是数字的范围如果超过unsigned int的最大值(4294967295)时,xdr_u_long失败。 这个场景主要用在unix时间戳上面,比如一款软件,设置有效期为100年。…...

Android Framework定制sim卡插入解锁pin码的界面
文章目录 手机设置SIM卡pin码一、安卓手机二、苹果手机 Android Framework中SIM卡pin码代码定位pin码提示文本位置定位pin码java代码位置 定制pin码framework窗口数字按钮 手机设置SIM卡pin码 设置 SIM 卡 PIN 码可以提高手机的安全性,防止他人在未经授权的情况下使…...

cc2530 Basic RF 讲解 和点灯讲解(1_1)
1. Basic RF 概述 Basic RF 是 TI 提供的一套简化版的无线通信协议栈,旨在帮助开发者快速搭建无线通信系统。它基于 IEEE 802.15.4 标准的数据包收发,但只用于演示无线设备数据传输的基本方法,不包含完整功能的协议。Basic RF 的功能限制包括…...

Android H5页面性能分析策略
文章目录 引言一、拦截资源加载请求以优化性能二、通过JavaScript代码监控资源下载速度三、使用vConsole进行前端性能调试四、使用Chrome DevTools调试Android端五、通过抓包分析优化网络性能六、总结 引言 在移动应用开发中,H5页面的性能直接影响到用户体验。本文…...

【前端面试】Typescript
Typescript面试题目回答 Typescript有哪些常用类型? Typescript的常用类型包括: 基本类型:boolean(布尔类型)、number(数字类型)、string(字符串类型)。特殊类型:nul…...
、手动管理(C语言)与所有权机制(Rust)(手动内存管理、手动管理内存))
程序语言的内存管理:垃圾回收GC(Java)、手动管理(C语言)与所有权机制(Rust)(手动内存管理、手动管理内存)
文章目录 程序语言的内存管理:垃圾回收、手动管理与所有权机制引言一、垃圾回收机制(GC)(Java)1. 什么是垃圾回收机制2. 垃圾回收的工作原理3. 优点与缺点4. 示例代码 二、手动管理内存的分配和释放(C语言&…...

研究生论文学习记录
文献检索 检索论文的网站 知网:找论文,寻找创新点paperswithcode :这个网站可以直接找到源代码 直接再谷歌学术搜索 格式:”期刊名称“ 关键词 在谷歌学术搜索特定期刊的关键词相关论文,可以使用以下几种方法&#…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞!!! 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用,因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型(VLMs)在字幕生成方面…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

JDK 17 新特性
#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持,不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的ÿ…...

SQL慢可能是触发了ring buffer
简介 最近在进行 postgresql 性能排查的时候,发现 PG 在某一个时间并行执行的 SQL 变得特别慢。最后通过监控监观察到并行发起得时间 buffers_alloc 就急速上升,且低水位伴随在整个慢 SQL,一直是 buferIO 的等待事件,此时也没有其他会话的争抢。SQL 虽然不是高效 SQL ,但…...

【JavaSE】多线程基础学习笔记
多线程基础 -线程相关概念 程序(Program) 是为完成特定任务、用某种语言编写的一组指令的集合简单的说:就是我们写的代码 进程 进程是指运行中的程序,比如我们使用QQ,就启动了一个进程,操作系统就会为该进程分配内存…...
