力扣每日一题打卡 684. 冗余连接
树可以看成是一个连通且 无环 的 无向 图。
给定往一棵 n 个节点 (节点值 1~n) 的树中添加一条边后的图。添加的边的两个顶点包含在 1 到 n 中间,且这条附加的边不属于树中已存在的边。图的信息记录于长度为 n 的二维数组 edges ,edges[i] = [ai, bi] 表示图中在 ai 和 bi 之间存在一条边。
请找出一条可以删去的边,删除后可使得剩余部分是一个有着 n 个节点的树。如果有多个答案,则返回数组 edges 中最后出现的那个。
题目意思说人话就是找到一条删去后仍然联通的边。所以最简单的思路就是从后往前尝试一条条删,找到删掉之后仍然联通的边就返回。至于怎么找一个图是否联通那可太简单了,BFS,DFS,并查集啥的都可以。所以我最开始想的就是暴力用DFS去找。虽然真正写出来了才意识到这么做好像时间复杂度太高了,说不定会超时,不过写都写了就干脆写完再说。没想到交上去居然直接过了,只能说力扣的数据太水了。下面给出代码。
class Solution {
public:vector<int> findRedundantConnection(vector<vector<int>>& edges) {n = edges.size();vector<vector<bool>> ma(n + 1, vector<bool>(n + 1, false));for (auto i:edges){ma[i[0]][i[1]] = ma[i[1]][i[0]] = 1;}for (int k=n-1; k>=0; --k){vector<int> i = edges[k];ma[i[0]][i[1]] = ma[i[1]][i[0]] = 0;if (check(ma)){return i;}ma[i[0]][i[1]] = ma[i[1]][i[0]] = 1;}return edges[0];}
private:int n;bool check(vector<vector<bool>> ma){bool flag[n+1];for (int i=1; i<=n; i++) flag[i] = false;stack<int> sta;sta.push(1);flag[1] = true;while (!sta.empty()){int pt = sta.top();sta.pop();for (int i=1; i<=n; i++){if (ma[pt][i] == true){if (flag[i] == false){sta.push(i), flag[i]=true;}}}}for (int i=1; i<=n; i++){if (flag[i]==false) return false;}return true;}
};本来我还想着超时之后就改成用邻接表去存的,按这个题的数据范围,邻接表应该是不会超时的。不过既然邻接矩阵已经过了,我也就懒得再改了。
毕竟这个题目还有更简单的方法可以实现,那就是并查集。(没学过并查集的自行百度)
思路是一条条尝试加边,判断两个点是否在同一个连通分量里面,如果在就可以直接返回这条边了,如果不在就把这条边加进去。因为题目保证只有n条边,所以这个方法找到的那条边一定是最后那条。
class Solution {
public:int find(int x){if (tree[x] != x) return find(tree[x]);return x;}void unite(int x, int y){int tx=find(x), ty=find(y);tree[tx]=ty;}vector<int> findRedundantConnection(vector<vector<int>>& edges) {const int n=edges.size();tree.clear();tree.resize(n+1);for (int i=1; i<=n; i++) tree[i]=i;for (auto i:edges){int f0=find(i[0]), f1=find(i[1]);if (f0 == f1){return i;}unite(i[0], i[1]);}return edges[0];}
private:vector<int> tree;
};这代码甚至比用DFS还要更简洁。
因为没有进行任何优化,就连路径压缩都没做,所以这个并查集的查找时间复杂度在最坏情况下是O(n)。所以本程序的时间复杂度为O(n*n), 空间复杂度是O(n)
当然,还可以进一步使用路径压缩和按秩合并进行优化。经过优化后的并查集操作的时间复杂度是O(α(n)), α是反阿克曼函数。可以认为优化后的并查集几乎是常数时间复杂度,也就是说这题如果用优化后的并查集,时间复杂度可以看成是接近O(n)的!虽然严格来说是O(n*α(n))。优雅的并查集
相关文章:

力扣每日一题打卡 684. 冗余连接
树可以看成是一个连通且 无环 的 无向 图。 给定往一棵 n 个节点 (节点值 1~n) 的树中添加一条边后的图。添加的边的两个顶点包含在 1 到 n 中间,且这条附加的边不属于树中已存在的边。图的信息记录于长度为 n 的二维数组 edges ,edges[i] …...

什么是微服务中的反应性扩展?
大家好,我是锋哥。今天分享关于【什么是微服务中的反应性扩展?】面试题?希望对大家有帮助; 什么是微服务中的反应性扩展? Reactive Extensions 也称为 Rx。这是一种设计方法,我们通过调用多个服务来收集结果…...

【MyBatis】MyBatis-config标签详解
目录 MyBatis配置文件标签详解configuration标签properties标签typeAliases标签environments标签environment标签transactionManager标签dataSource标签mappers标签 MyBatis配置文件标签详解 我们在使用MyBatis框架的时候需要一个配置文件——MyBatis-config.xml来告诉MyBatis…...

使用AVPlayer进行音频播放开发基础设计
在使用AvPlayer进行设计之前,需要获取相应对象,后期围绕该对象展开操作 const player await media.createAVPlayer() 然后对播放器进行初始化设置: player.on(stateChange, (state) > {switch (state) {case initialized:player.prepar…...

API网关的作用--为什么微服务需要一个API网关?
微服务网关核心作用就是协议转换、安全隔离和流量控制 微服务架构中,API网关作为系统的入口点,可以统一处理所有客户端请求。 1)协议转换:它能够支持多种通信协议(如HTTP、gRPC等)之间的相互转换ÿ…...

[0154].第5节:IDEA中创建Java Web工程
我的后端学习大纲 IDEA大纲 1.1.IDEA中配置Tomcat: 1.找打setting: 2.配置Tomcat Server的位置: 3.这里配置Tomcat的名称以及配置应用服务器的位置。根据自己Tomcat的安装位置决定 4.配置好后,如下图所示 1.2.创建Web工程: 1.建…...

React03 组件 Props
组件 & Props React 组件函数( Function )组件类( Class )组件 Props将 props 传递给子组件在子组件中读取 props给 prop 指定一个默认值使用 JSX 展开语法传递 props React 组件 组件本质上就是类和函数,但是与常…...

多线程——线程安全的集合类
目录 前言 一、多线程环境使用 ArrayList 1.进行加锁 2.使用 SynchronizedList 类 3.使用 CopyOnWriteArrayList 类 二、多线程环境使用队列 1.进行加锁 2.使用阻塞队列 三、多线程环境使用哈希表 1.Hashtable 2.ConcurrentHashMap (1)缩小锁…...

自动化数据库管理:如何通过存储过程动态创建 MySQL 对象
在当今数据驱动的世界中,高效的数据库管理至关重要。本文将展示如何通过存储过程自动化地创建各种 MySQL 数据库对象,包括数据表、视图、字段、索引、约束、存储过程、定时器和事件。通过这些方法,我们可以快速响应业务需求,提高数…...

480p 720p 1080p 2k 4k 8k 12k分辨率视频分别占用多大带宽?
技术背景 好多开发者,在设置视频编码参数的时候,对不同分辨率的带宽设置,缺乏相关的经验,实际上,视频分辨率与所需带宽之间的关系受到多个因素的影响,包括视频编码方式、帧率、视频内容的动态程度等。下面…...

unity中GameObject介绍
在 Unity 中,Cube和Sphere等基本几何体是 Unity 引擎的内置预制体(Prefabs),它们属于 Unity 中的GameObject 系统,可以在 Unity 的 Hierarchy 视图或 Scene 视图中右键点击,然后在弹出的菜单中选择 3D Obje…...

洛谷——P8468 [Aya Round 1 C] 文文的构造游戏(01构造问题)
P8468 [Aya Round 1 C] 文文的构造游戏 题目描述 [Aya Round 1 C] 文文的构造游戏 - 洛谷 运行代码(暴力枚举)——超时 #include <stdio.h> #define ll long long const int N 1e6 5; // 计算数组元素的异或和 ll xorSum(ll arr[], int n) {l…...

双击热备和负载均衡的区别
区别: 双机热备 (heartbeat):对同一应用来讲,永远是主机应用启动,备机应用停止的一主一备模式(两台通常叫双击热备,多台称为高可用) 负载均衡:两台/多台服务器 上同一个应用系统同时工作,分担负…...

如何使用 cPanel 部署 WordPress临时网站
对于依赖WordPress站点或WooCommerce商店的企业来说,在生产环境中直接修改站点风险很大。而WordPress的临时网站是一个更安全的选择,可以通过使用临时网站进行编辑来规避风险。 在本文中,我们将详细介绍WordPress临时网站的相关知识、使用临时…...
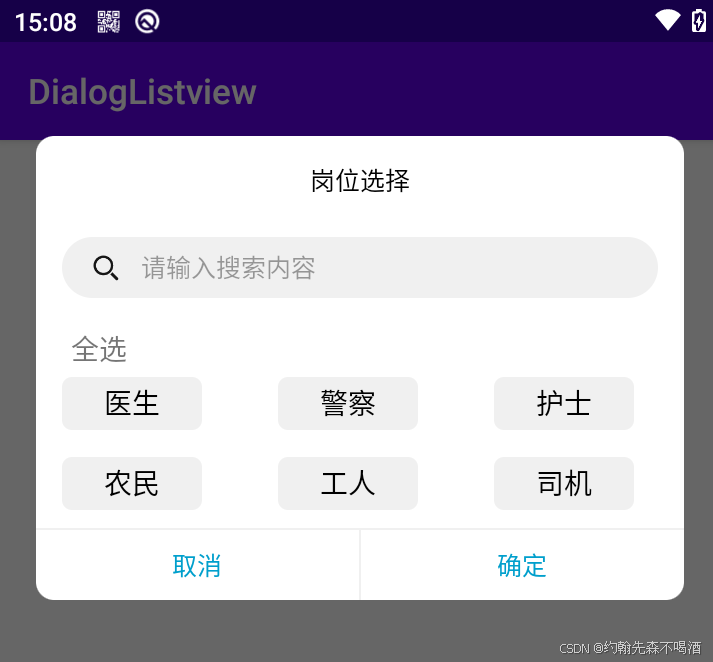
Android 自定义 Dialog 实现列表 单选,多选,搜索
前言 在Android开发中,通过对话框让用户选择,筛选信息是很方便也很常见的操作。本文详细介绍了如何使用自定义 Dialog、RecyclerView 以及自定义搜索框 来实现选中状态和用户交互,文中大本分代码都有明确注释,主打一个简单明了&a…...

下载地址合辑(持续更新)
下载地址合辑 汇总OSG相关地址Visual Studio Qt 地址qt插件安装失败 Boost库boost库编译步骤 FFmpeg 地址osg编译库 常用的下载地址: 汇总 vlc 地址: https://www.videolan.org/vlc/index.zh_CN.html visual 地址:https://my.visualstudio.…...

Android Kotlin 高阶函数详解及其在协程中的应用
文章目录 1. 引言2. 什么是高阶函数?3. 高阶函数的基础用法3.1 传递函数作为参数3.2 Lambda 表达式3.3 匿名函数3.4 返回函数 4. 高阶函数的深入用法4.1 函数组合4.2 内联函数4.3 高阶扩展函数 5. Kotlin 高阶函数的对比优势5.1 与 Java 的对比5.2 与 JavaScript 的…...

CSS基础—网页布局(重点!)
1、两列布局 (1)概念 经典两列布局是指一种网页布局方式,其中一列宽度固定,另一列宽度自适应。 这种布局方式在网页设计中非常常见,因为它能够提供良好的视觉效果和用户体验。 如图所示: 页面顶部放置一…...

【Fargo】17:vs工程转qt构建:QT6 不支持32bit转向qt5.15.2
vs2022的console 工程加入qt支持后使用qt15.2 的vs2019 库,变为一个qt界面程序。最终效果 一些参考 qt5的项目搭建 qt5 最多支持到vs2019 qt6 最新 已经支持vs2022 国内还是以qt5.15为主 升级qt的vstools...

智能电表蓝牙芯片方案
RAMSUN基于自研射频技术和基带算法提供蓝牙MCU。蓝牙MCU配套成熟的网络协议栈和丰富的示例代码及多平台APP工具。部分芯片型号无需二次开发,即连即用;提供特色蓝牙/串口/USB三通芯片,为更多复杂无线应用赋能。 应用案例说明: BLE方便用户直接…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

ArcGIS Pro制作水平横向图例+多级标注
今天介绍下载ArcGIS Pro中如何设置水平横向图例。 之前我们介绍了ArcGIS的横向图例制作:ArcGIS横向、多列图例、顺序重排、符号居中、批量更改图例符号等等(ArcGIS出图图例8大技巧),那这次我们看看ArcGIS Pro如何更加快捷的操作。…...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...

华硕a豆14 Air香氛版,美学与科技的馨香融合
在快节奏的现代生活中,我们渴望一个能激发创想、愉悦感官的工作与生活伙伴,它不仅是冰冷的科技工具,更能触动我们内心深处的细腻情感。正是在这样的期许下,华硕a豆14 Air香氛版翩然而至,它以一种前所未有的方式&#x…...

A2A JS SDK 完整教程:快速入门指南
目录 什么是 A2A JS SDK?A2A JS 安装与设置A2A JS 核心概念创建你的第一个 A2A JS 代理A2A JS 服务端开发A2A JS 客户端使用A2A JS 高级特性A2A JS 最佳实践A2A JS 故障排除 什么是 A2A JS SDK? A2A JS SDK 是一个专为 JavaScript/TypeScript 开发者设计的强大库ÿ…...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...
提供了哪些便利?)
现有的 Redis 分布式锁库(如 Redisson)提供了哪些便利?
现有的 Redis 分布式锁库(如 Redisson)相比于开发者自己基于 Redis 命令(如 SETNX, EXPIRE, DEL)手动实现分布式锁,提供了巨大的便利性和健壮性。主要体现在以下几个方面: 原子性保证 (Atomicity)ÿ…...

提升移动端网页调试效率:WebDebugX 与常见工具组合实践
在日常移动端开发中,网页调试始终是一个高频但又极具挑战的环节。尤其在面对 iOS 与 Android 的混合技术栈、各种设备差异化行为时,开发者迫切需要一套高效、可靠且跨平台的调试方案。过去,我们或多或少使用过 Chrome DevTools、Remote Debug…...
