Leetcode|454.四数相加II ● 383. 赎金信 ● 15. 三数之和 ● 18. 四数之和
15.三数之和
哈希解法:
用俩个for循环求出,所需的a和b,再用哈希表,判断剩余的那个c是否在数组
class Solution {
public:vector<vector<int>> threeSum(vector<int>& nums) {vector<vector<int>> result;sort(nums.begin(), nums.end());// 找出a + b + c = 0// a = nums[i], b = nums[j], c = -(a + b)for (int i = 0; i < nums.size(); i++) {// 排序之后如果第一个元素已经大于零,那么不可能凑成三元组if (nums[i] > 0) {break;}if (i > 0 && nums[i] == nums[i - 1]) { //三元组元素a去重continue;}unordered_set<int> set;for (int j = i + 1; j < nums.size(); j++) {if (j > i + 2&& nums[j] == nums[j-1]&& nums[j-1] == nums[j-2]) { // 三元组元素b去重continue;}int c = 0 - (nums[i] + nums[j]);if (set.find(c) != set.end()) {result.push_back({nums[i], nums[j], c});set.erase(c);// 三元组元素c去重} else {set.insert(nums[j]);}}}return result;}
};双指针解法:
class Solution {
public:vector<vector<int>> threeSum(vector<int>& nums) {vector<vector<int>> result;sort(nums.begin(),nums.end());for(int i = 0;i<nums.size();i++){if(nums[i] > 0){return result;}//i元素的去重if(i > 0&& nums[i] == nums[i-1]){continue;}int left = i + 1;int right = nums.size() - 1;//left 和 right元素的去重,相同就停止,因为要求的是三个元素,而非俩个元素while(right > left){if(nums[i] + nums[left] + nums[right] >0){right--;}else if(nums[i] + nums[left] + nums[right] < 0){left++;}else{result.push_back(vector<int>{nums[i],nums[left],nums[right]});//去重逻辑应该放在找到一个三元组之后//防止漏掉{0,0,0}这个三元组while(right>left&&nums[right] == nums[right-1]) right--;while(right>left&&nums[left] == nums[left+1]) left++;left++;right--;}}}return result;}
};454.四数相加
class Solution {
public:int fourSumCount(vector<int>& nums1, vector<int>& nums2, vector<int>& nums3, vector<int>& nums4) {unordered_map <int,int> umap; //key为a和b的值,value为a和b的值出现的次数//记录,a和b and a和b出现的次数for(int a: nums1){for(int b: nums2){umap[a+b]++;//俩数的和and次数}}int count = 0;for(int c:nums3){for(int d:nums4){if(umap.find(0 - (c+d))!=umap.end()){count += umap[0-(c+d)];}}}return count;}
};18.四数之和
class Solution {
public:vector<vector<int>> fourSum(vector<int>& nums, int target) {vector<vector<int>> result;sort(nums.begin(),nums.end());for(int k = 0;k < nums.size();k++){//剪枝 if(nums[k] > target) return result;这错误的,target不为0// 去重if(k > 0 && nums[k] == nums[k-1]){continue;}for(int i = k + 1;i < nums.size();i++){//去重if(i > k + 1 && nums[i] == nums[i-1]){continue;}int left = i + 1;int right = nums.size() - 1;while(right > left){if(nums[k] + nums[i] > target - nums[left] - nums[right]){right--;}else if(nums[k] + nums[i] < target - nums[left] - nums[right]){left++;}else{result.push_back(vector<int>{nums[k],nums[i],nums[left],nums[right]});while(right>left&&nums[right] == nums[right-1]) right--;while(right>left&&nums[left] == nums[left+1]) left++;right--;left++;}}}}return result;}
};383,赎金,此题与求解异位字母是同种思路
class Solution {
public:bool canConstruct(string ransomNote, string magazine) {int record[26] = {0};if(ransomNote.size() > magazine.size()) return false;for(int i = 0;i < magazine.length();i++){record[magazine[i] - 'a']++; //统计个数,映射求结果}for(int j = 0;j<ransomNote.length();j++){record[ransomNote[j] - 'a']--;}for(int i = 0;i < 26; i++){if(record[i] < 0){return false;}}return true;}
};相关文章:

Leetcode|454.四数相加II ● 383. 赎金信 ● 15. 三数之和 ● 18. 四数之和
15.三数之和 哈希解法: 用俩个for循环求出,所需的a和b,再用哈希表,判断剩余的那个c是否在数组 class Solution { public:vector<vector<int>> threeSum(vector<int>& nums) {vector<vector<int>…...

使用ceph-csi把ceph-fs做为k8s的storageclass使用
背景 ceph三节点集群除了做为对象存储使用,计划使用cephfs替代掉k8s里面现有的nfs-storageclass。 思路 整体实现参考ceph官方的ceph csi实现,这套环境是arm架构的,即ceph和k8s都是在arm上实现。实测下来也兼容。 ceph-fs有两种两种挂载方…...
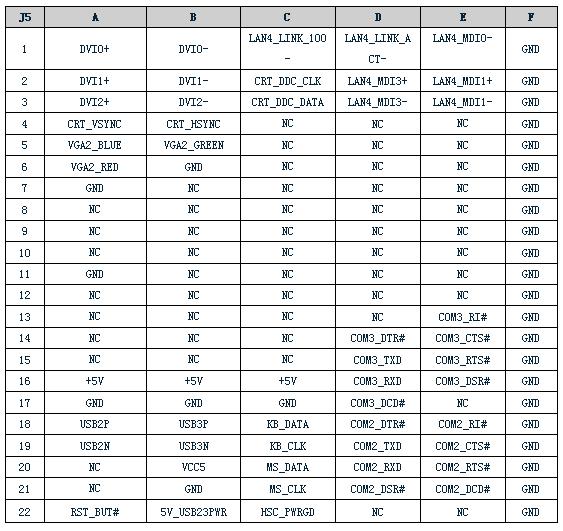
太速科技-212-RCP-601 CPCI刀片计算机
RCP-601 CPCI刀片计算机 一、产品简介 RCP-601是一款基于Intel i7双核四线程的高性能CPCI刀片式计算机,同时,将CPCI产品的欧卡结构及其可靠性、可维护性、可管理性与计算机的抗振动、抗冲击、抗宽温环境急剧变化等恶劣环境特性进行融合。产品特别…...

【解决 Windows 下 SSH “Bad owner or permissions“ 错误及端口转发问题详解】
使用 Windows 连接远程服务器出现 Bad owner or permissions 错误及解决方案 在 Windows 系统上连接远程服务器时,使用 SSH 可能会遇到以下错误: Bad owner or permissions on C:\Users\username/.ssh/config这个问题通常是由于 SSH 配置文件 .ssh/con…...

使用预训练的BERT进行金融领域问答
获取更多完整项目代码数据集,点此加入免费社区群 : 首页-置顶必看 1. 项目简介 本项目旨在开发并优化一个基于预训练BERT模型的问答系统,专注于金融领域的应用。随着金融市场信息复杂性和规模的增加,传统的信息检索方法难以高效…...

ReactOS系统中MM_REGION结构体的声明
ReactOS系统中MM_REGION结构体的声明 ReactOS系统中MM_REGION结构体的声明 文章目录 ReactOS系统中MM_REGION结构体的声明MM_REGION MM_REGION typedef struct _MM_REGION {ULONG Type;//MEM_COMMIT,MEM_RESERVEULONG Protect;//PAGE_READONLYY,PAGE_READ_WRITEULONG Length;…...

web相关知识学习笔记
一, web安全属于网络信息安全的一个分支,www即全球广域网,也叫万维网,是一个分布式图形信息系统 二, 1.①安全领域,通常将用户端(浏览器端)称为前端,服务器端称为后端 ②…...

App测试环境部署
一.JDK安装 参考以下AndroidDevTools - Android开发工具 Android SDK下载 Android Studio下载 Gradle下载 SDK Tools下载 二.SDK安装 安装地址:https://www.androiddevtools.cn/ 解压 环境变量配置 变量名:ANDROID_SDK_HOME 参考步骤: A…...

【论文阅读】Tabbed Out: Subverting the Android Custom Tab Security Model
论文链接:Tabbed Out: Subverting the Android Custom Tab Security Model | IEEE Conference Publication | IEEE Xplore 总览 “Tabbed Out: Subverting the Android Custom Tab Security Model” 由 Philipp Beer 等人撰写,发表于 2024 年 IEEE Symp…...

2025 - AI人工智能药物设计 - 中药网络药理学和毒理学的研究
中药网络药理学和毒理学的研究 TCMSP:https://old.tcmsp-e.com/tcmsp.php 然后去pubchem选择:输入Molecule Name 然后进行匹配:得到了smiles 再次通过smiles:COC1C(CC(C2C1OC(CC2O)C3CCCCC3)O)O 然后再次输入:http…...

iwebsec靶场 XSS漏洞通关笔记
目录 前言 1.反射性XSS 2.存储型XSS 3.DOM型XSS 第01关 反射型XSS漏洞 1.打开靶场 2.源码分析 3.渗透 第02关 存储型XSS漏洞 1.打开靶场 2.源码分析 4.渗透 方法1: 方法2 方法3 第03关 DOM XSS漏洞 1.打开靶场 2.源码分析 3.渗透分析 3.渗透过程…...

设计模式-单例模型(单件模式、Singleton)
单例模式是一种创建型设计模式, 让你能够保证一个类只有一个实例, 并提供一个访问该实例的全局节点。 单例模式同时解决了两个问题, 所以违反了单一职责原则: 保证一个类只有一个实例。 为什么会有人想要控制一个类所拥有的实例…...

笔记本双系统win10+Ubuntu 20.04 无法调节亮度亲测解决
sudo add-apt-repository ppa:apandada1/brightness-controller sudo apt-get update sudo apt-get install brightness-controller-simple 安装好后找到一个太阳的图标,就是这个软件,打开后调整brightness,就可以调整亮度,可…...

零基础Java第十一期:类和对象(二)
目录 一、对象的构造及初始化 1.1. 就地初始化 1.2. 默认初始化 1.3. 构造方法 二、封装 2.1. 封装的概念 2.2. 访问限定符 2.3. 封装扩展之包 三、static成员 3.1. 再谈学生类 3.2. static修饰成员变量 一、对象的构造及初始化 1.1. 就地初始化 在声明成员变…...
 python笔记扩展)
NumPy包(下) python笔记扩展
9.迭代数组 nditer 是 NumPy 中的一个强大的迭代器对象,用于高效地遍历多维数组。nditer 提供了多种选项和控制参数,使得数组的迭代更加灵活和高效。 控制参数 nditer 提供了多种控制参数,用于控制迭代的行为。 1.order 参数 order 参数…...

极狐GitLab 17.5 发布 20+ 与 DevSecOps 相关的功能【一】
GitLab 是一个全球知名的一体化 DevOps 平台,很多人都通过私有化部署 GitLab 来进行源代码托管。极狐GitLab 是 GitLab 在中国的发行版,专门为中国程序员服务。可以一键式部署极狐GitLab。 学习极狐GitLab 的相关资料: 极狐GitLab 官网极狐…...

Oracle 第1章:Oracle数据库概述
在讨论Oracle数据库的入门与管理时,我们可以从以下几个方面来展开第一章的内容:“Oracle数据库概述”,包括数据库的历史与发展,Oracle数据库的特点与优势。 数据库的历史与发展 数据库技术的发展可以追溯到上世纪50年代…...

7、Nodes.js包管理工具
四、包管理工具 4.1 npm(Node Package Manager) Node.js官方内置的包管理工具。 命令行下打以下命令: npm -v如果返回版本号,则说明npm可以正常使用 4.1.1npm初始化 #在包所在目录下执行以下命令 npm init #正常初始化,手动…...

网络地址转换——NAT技术详解
网络地址转换——NAT技术详解 一、引言 随着互联网的飞速发展,IP地址资源日益紧张。为了解决IP地址资源短缺的问题,NAT(Network Address Translation,网络地址转换)技术应运而生。NAT技术允许一个私有IP地址的网络通…...

问:数据库存储过程优化实践~
存储过程优化是提高数据库性能的关键环节。通过精炼SQL语句、合理利用数据库特性、优化事务管理和错误处理,可以显著提升存储过程的执行效率和稳定性。以下是对存储过程优化实践点的阐述,结合具体示例,帮助大家更好地理解和实施这些优化策略。…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...

2025年渗透测试面试题总结-腾讯[实习]科恩实验室-安全工程师(题目+回答)
安全领域各种资源,学习文档,以及工具分享、前沿信息分享、POC、EXP分享。不定期分享各种好玩的项目及好用的工具,欢迎关注。 目录 腾讯[实习]科恩实验室-安全工程师 一、网络与协议 1. TCP三次握手 2. SYN扫描原理 3. HTTPS证书机制 二…...

Razor编程中@Html的方法使用大全
文章目录 1. 基础HTML辅助方法1.1 Html.ActionLink()1.2 Html.RouteLink()1.3 Html.Display() / Html.DisplayFor()1.4 Html.Editor() / Html.EditorFor()1.5 Html.Label() / Html.LabelFor()1.6 Html.TextBox() / Html.TextBoxFor() 2. 表单相关辅助方法2.1 Html.BeginForm() …...

Vite中定义@软链接
在webpack中可以直接通过符号表示src路径,但是vite中默认不可以。 如何实现: vite中提供了resolve.alias:通过别名在指向一个具体的路径 在vite.config.js中 import { join } from pathexport default defineConfig({plugins: [vue()],//…...

Bean 作用域有哪些?如何答出技术深度?
导语: Spring 面试绕不开 Bean 的作用域问题,这是面试官考察候选人对 Spring 框架理解深度的常见方式。本文将围绕“Spring 中的 Bean 作用域”展开,结合典型面试题及实战场景,帮你厘清重点,打破模板式回答,…...

恶补电源:1.电桥
一、元器件的选择 搜索并选择电桥,再multisim中选择FWB,就有各种型号的电桥: 电桥是用来干嘛的呢? 它是一个由四个二极管搭成的“桥梁”形状的电路,用来把交流电(AC)变成直流电(DC)。…...

Spring Boot + MyBatis 集成支付宝支付流程
Spring Boot MyBatis 集成支付宝支付流程 核心流程 商户系统生成订单调用支付宝创建预支付订单用户跳转支付宝完成支付支付宝异步通知支付结果商户处理支付结果更新订单状态支付宝同步跳转回商户页面 代码实现示例(电脑网站支付) 1. 添加依赖 <!…...
