裴蜀定理与欧几里得算法——蓝桥杯真题中的应用
目录
- 裴蜀定理(Bézout's Theorem)
- 1、定义
- 2、推论
- 3、欧几里得算法
- 4、多个整数的裴蜀定理扩展
- 真题挑战
- 解题思路
- 代码实现与详细注释
- 代码解析
裴蜀定理(Bézout’s Theorem)
1、定义
对于任意两个整数 a 和 b ,如果它们的最大公约数是 d,那么可以找到整数 x 和 y,使得 a和 b 的最大公约数 d 可以表示为它们的整数线性组合。
即: gcd(a,b)=ax+by
gcd(a,b)表示a和b的最大公约数。
2、推论
对于两个正整数 a 和b(且互质,即最大公约数gcd(a,b)为 1),我们可以通过裴蜀定理推导出:无法表示成 a 和 b 的非负整数线性组合的最大数是axb - a - b。换句话说,任何大于 axb - a - b的数都可以用 a 和 b 的非负整数倍表示。
3、欧几里得算法
求两个数的最大公约数,对经典的算法就是欧几里得算法:
public class Main {//欧几里得算法private static int gcd(int a,int b){if(b==0)return a;else return gcd(b,a%b);}public static void main(String[] args) {Scanner in=new Scanner(System.in);int a=in.nextInt();int b=in.nextInt();int ans=gcd(a,b);System.out.println(ans);}
}
4、多个整数的裴蜀定理扩展
对于多个整数,裴蜀定理仍然适用:
对于一组整数 ( a1, a2, … , an ),如果我们想找到整数 ( x1, x2, …, xn ) 使得:
d = a 1 x 1 + a 2 x 2 + ⋯ + a n x n d = a_1 x_1 + a_2 x_2 + \dots + a_n x_n d=a1x1+a2x2+⋯+anxn
其中 d 是这组整数的最大公约数,即 ( d = gcd(a1, a2, …, an) ),那么这样的 ( x1, x2,…, xn ) 一定存在。并且如果d==1,那么一定存在数字MAX,a这个集合可以表示仍和大于MAX的数字。并且这个MAX,一定小于原先二元组推导的最大不可表示的数字axb - a- b
真题挑战
第8届蓝桥杯_B组_Java_第七题:包子凑数

题目要求我们判断给定不同大小的包子笼是否可以凑出某个数量的包子,进而计算出凑不出的包子数量。如果无法凑出无限多种数量的包子,输出INF;否则输出所有无法凑出的数量的个数。
解题思路
-
判断是否存在无限个凑不出的情况:通过最大公约数(GCD)判断所有笼子的包子数量是否能组合成任意数量的包子。如果所有笼子的数量的GCD大于1,那么凑不出这个GCD的倍数的数字,这就意味着存在无限多的数量是无法凑出的,输出
INF。 -
动态规划(DP)判断可表示的包子数量:如果笼子的数量的GCD为1,我们可以利用动态规划来记录可凑出的包子数量。用一个布尔数组
dp表示不同的包子数量是否可以凑出,其中dp[i]为true表示可以凑出i个包子,false表示无法凑出。 -
遍历每种蒸笼数量更新
dp数组:对每种蒸笼大小A[i],我们更新dp数组,遍历dp数组并设定dp[j + A[i]] = true,表示可以通过加上A[i]来凑出数量j + A[i]。 -
计算结果:遍历
dp数组,统计所有无法凑出的包子数量。
代码实现与详细注释
以下是实现代码,含详细注释。
import java.util.Scanner;public class Main {static int N = 10000; // 设定一个足够大的数组大小,用于记录可凑出的包子数量static int n; // 蒸笼的种类数static int g; // 所有蒸笼包子数量的最大公约数static boolean[] dp = new boolean[N]; // 动态规划数组,dp[i]为true表示可以凑出i个包子static int[] arr; // 用于存储每种蒸笼的包子数量// 计算两个数的最大公约数(欧几里得算法)private static int gcd(int a, int b) {if (b == 0) return a;return gcd(b, a % b);}public static void main(String[] args) {Scanner in = new Scanner(System.in);n = in.nextInt(); // 读取蒸笼种类数arr = new int[n]; // 初始化蒸笼包子数量的数组dp[0] = true; // 初始状态,0个包子可以表示(即不选择任何蒸笼)for (int i = 0; i < n; i++) {arr[i] = in.nextInt(); // 读取每种蒸笼的包子数量g = gcd(arr[i], g); // 更新所有蒸笼包子数量的最大公约数for (int j = 0; j < N - arr[i]; j++) { // 遍历当前dp数组的可凑出数量if (dp[j]) dp[j + arr[i]] = true; // 更新dp数组表示可以凑出j + arr[i]个包子}}// 判断是否有无限个无法凑出的数量if (g != 1) {System.out.print("INF");return;}// 如果g == 1,统计所有无法凑出的包子数量long ans = 0; // 用于统计无法凑出的包子数量for (boolean is : dp) { // 遍历dp数组if (!is) ans++; // 如果dp[i]为false,表示i个包子无法凑出,计数+1}System.out.print(ans); // 输出无法凑出的包子数量}
}
代码解析
-
最大公约数的计算:利用欧几里得算法,通过不断递归计算两个数的GCD。如果所有蒸笼的数量的GCD不为1,则有无限多个数量无法凑出,直接输出
INF(裴蜀定理)。 -
动态规划数组
dp的更新:对于每种蒸笼数量A[i],遍历当前dp数组中可凑出的数量j,如果dp[j]为true,则可以凑出数量j + A[i]。通过这种方式,我们记录了所有可以凑出的数量。 -
结果统计:在确定GCD为1的情况下,遍历
dp数组,统计false的项即为无法凑出的数量。
裴蜀定理的应用:本题中利用了裴蜀定理的推论,若GCD为1,可以表示任意大的数,从而限制了无法表示的数量。
相关文章:

裴蜀定理与欧几里得算法——蓝桥杯真题中的应用
目录 裴蜀定理(Bzouts Theorem)1、定义2、推论3、欧几里得算法4、多个整数的裴蜀定理扩展 真题挑战解题思路代码实现与详细注释代码解析 裴蜀定理(Bzout’s Theorem) 1、定义 对于任意两个整数 a 和 b ,如果它们的最…...

冯诺依曼架构及CPU相关概念
一. 操作系统的概念 1. 概念 操作系统(Operating System). 首先, 所有的计算机都是由软件和硬件构成的. 而操作系统就是许许多多软件中的一种软件, 操作系统可以看作是由两部分组成: 操作系统内核系统级应用程序. 2. 作用 (1) 管理硬件设备, 调度和协调各个硬件之间的工作.…...

智能管线巡检系统:强化巡检质量,确保安全高效运维
线路巡检质量的监控是确保线路安全、稳定运行的重要环节。为了有效监控巡检质量,采用管线巡检系统是一种高效、科学的手段。以下是对如何通过管线巡检系统实现线路巡检质量监控的详细分析: 一、巡检速度监控 管线巡检系统能够实时监控巡检人员的巡检速度…...

React写关键字高亮的三个方案
1.js正则replaceAlldangerouslySetInnerHTML{{ __html: xxx }}危险属性 步骤最简单,但是是危险属性,不推荐使用,项目中实在没有头绪,可以使用它应急 通过useMemo计算得到新的状态值,赋值给dangerouslySetInnerHTML属性的__html 关键代码: const [state1, setState1] useSt…...
重塑在线软件开发新纪元:集成高效安全特性,深度解析与评估会员与促销管理系统的系统架构设计
案例 阅读以下关于软件架构设计与评估的叙述,回答问题1和问题2。 【题目】 某电子商务公司拟升级其会员与促销管理系统,向用户提供个性化服务,提高用户的粘性。在项目立项之初,公司领导层一致认为本次升级的主要目标是提升会员管…...

多层感知机的从零实现与softmax的从零实现(真·0000零基础)
今天再读zh.d2l书(4.2. 多层感知机的从零开始实现 — 动手学深度学习 2.0.0 documentation), 看了关于多层感知机的从零实现与softmax的从零实现 目录 mlp从零实现, 点击“paddle”的代码 点击“torch”的代码 训练 参数解…...

【Rust练习】18.特征 Trait
练习题来自:https://practice-zh.course.rs/generics-traits/traits.html 1 // 完成两个 impl 语句块 // 不要修改 main 中的代码 trait Hello {fn say_hi(&self) -> String {String::from("hi")}fn say_something(&self) -> String; }str…...

【自动化测试之oracle数据库】MacOs如何安装oracle- client
操作系统为Mac OS,本地在pycharm上跑自动化脚本时,因为有操作oracle数据库的部分,所以需要安装oracle数据库的客户端,并install cx_oracle,本文主要介绍如何在macOS上完成安装,并在python自动化测试代码中配置…...

Spring MVC的MultipartFile
定义 MultipartFile接口是Spring MVC中用来处理上传文件的接口,它提供了访问上传文件内容、文件名称、文件大小等信息的方法。 源码: package org.springframework.web.multipart;import java.io.File; import java.io.IOException; import java.io.I…...

●Leetcode| 242.有效的字母异位词 ● 349. 两个数组的交集 ● 202. 快乐数● 1. 两数之和
242,该题目中数组范围比较短,可以数组使用并不会占太多的空间,利用数组的映射,查找到自己所需要的字符 class Solution { public:bool isAnagram(string s, string t) {int record[26] {0};for(int i0;i<s.size();i){record[s[i] - a];/…...

关于算法的时间复杂度和空间复杂度的分析
由于最近开始准备蓝桥杯(python组),开始对编程基础进行一些复习,当我发现蓝桥对大多数题目程序运行时间及大小有要求时,我知道我不得不考虑性能问题,而不是能跑就行🤓 写下这篇文章希望对其他同志有帮助吧 什么是算法…...

深入浅出 C++ STL:解锁高效编程的秘密武器
引言 C 标准模板库(STL)是现代 C 的核心部分之一,为开发者提供了丰富的预定义数据结构和算法,极大地提升了编程效率和代码的可读性。理解和掌握 STL 对于 C 开发者来说至关重要。以下是对 STL 的详细介绍,涵盖其基础知…...

2024年1024程序人生总结
2024-1024 0.大环境0.1.经济0.2.战争 1.我的程序人生1.1.游戏 2.节日祝福 0.大环境 今年的1024最大的感触就是没有节日氛围,往年公司还会准备节日礼物,今年没有,由此可见大环境有多么糟糕。 除此之外,就是到公司应聘的程序员越来…...

【p2p、分布式,区块链笔记 分布式容错算法】: 拜占庭将军问题+实用拜占庭容错算法PBFT
papercodehttps://pmg.csail.mit.edu/papers/osdi99.pdfhttps://github.com/luckydonald/pbft 其他相关实现:This is an implementation of the Pracltical Byzantine Fault Tolerance protocol using PythonAn implementation of the PBFT consensus algorithm us…...
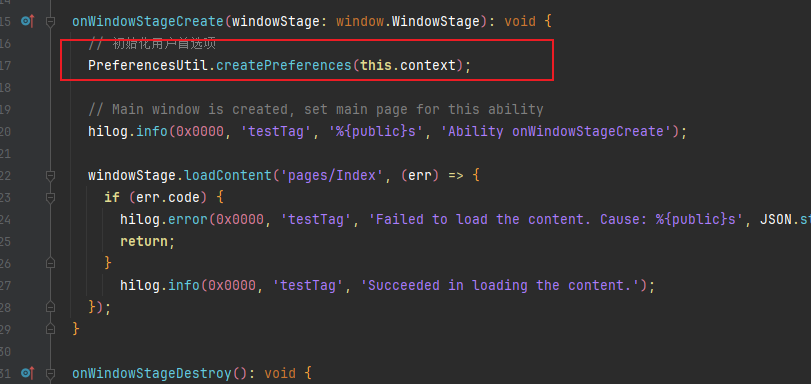
鸿蒙NEXT开发-应用数据持久化之用户首选项(基于最新api12稳定版)
注意:博主有个鸿蒙专栏,里面从上到下有关于鸿蒙next的教学文档,大家感兴趣可以学习下 如果大家觉得博主文章写的好的话,可以点下关注,博主会一直更新鸿蒙next相关知识 专栏地址: https://blog.csdn.net/qq_56760790/…...

人工智能_神经网络103_感知机_感知机工作原理_感知机具备学习能力_在学习过程中自我调整权重_优化效果_多元线性回归_逻辑回归---人工智能工作笔记0228
由于之前一直对神经网络不是特别清楚,尤其是对神经网络中的一些具体的概念,包括循环,神经网络卷积神经网络以及他们具体的作用,都是应用于什么方向不是特别清楚,所以现在我们来做教程来具体明确一下。 当然在机器学习之后还有深度学习,然后在深度学习中对各种神经网络的…...

WISE:重新思考大语言模型的终身模型编辑与知识记忆机制
论文地址:https://arxiv.org/abs/2405.14768https://arxiv.org/abs/2405.14768 1. 概述 随着世界知识的不断变化,大语言模型(LLMs)需要及时更新,纠正其生成的虚假信息或错误响应。这种持续的知识更新被称为终身模型编…...

网络安全证书介绍
网络安全领域有很多专业的证书,可以帮助你提升知识和技能,增强在这个行业中的竞争力。以下是一些常见的网络安全证书: 1. CompTIA Security 适合人群:初级安全专业人员证书内容:基础的网络安全概念和实践,…...

【已解决】【hadoop】【hive】启动不成功 报错 无法与MySQL服务器建立连接 Hive连接到MetaStore失败 无法进入交互式执行环境
启动hive显示什么才是成功 当你成功启动Hive时,通常会看到一系列的日志信息输出到控制台,这些信息包括了Hive服务初始化的过程以及它与Metastore服务连接的情况等。一旦Hive完成启动并准备就绪,你将看到提示符(如 hive> &#…...

基于架设一台NFS服务器实操作业
架设一台NFS服务器,并按照以下要求配置 首先需要关闭防火墙和SELinux 1、开放/nfs/shared目录,供所有用户查询资料 赋予所有用户只读的权限,sync将数据同步写到磁盘上 在客户端需要创建挂载点,把服务端共享的文件系统挂载到所创建…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...

零基础在实践中学习网络安全-皮卡丘靶场(第九期-Unsafe Fileupload模块)(yakit方式)
本期内容并不是很难,相信大家会学的很愉快,当然对于有后端基础的朋友来说,本期内容更加容易了解,当然没有基础的也别担心,本期内容会详细解释有关内容 本期用到的软件:yakit(因为经过之前好多期…...
