单调栈应用介绍
单调栈应用介绍
- 定义
- 应用场景
- 实现模板
- 具体示例
- 下一个最大元素I
- 问题描述
- 问题分析
- 代码实现
- 柱状图中最大的矩形
- 问题描述
- 问题分析
- 代码实现
- 接雨水
- 问题描述
- 问题分析
- 代码实现
- 最大宽度坡
- 问题描述
- 问题分析
- 代码实现
- 132模式
- 问题描述
- 问题分析
- 代码实现
定义
栈(Stack)是另一种操作受限的线性表,只允许元素从栈的顶端进顶端出,具有后进先出(LIFO)的特性。但单调栈(Monotonic Stack)是一种特殊的栈,在满足栈特性的基础上,栈内元素从栈底到栈顶具有单调性。如果栈底到栈顶元素是单调递减,则称为单调递减栈;如果栈底到栈顶元素是单调递增,则称为单调递增栈。
单调栈具有以下特性:
- 新元素加入栈顶时,需要进行单调性维护,弹出不满足单调性的栈顶元素
- 当前解计算是在出栈的时候进行的
应用场景
- 下一个最大元素,对应单调递减栈
- 下一个最小元素,对应单调递增栈
- 上一个最大元素,反向入栈,即从数据尾部往前遍历,对应单调递减栈
- 上一个最小元素,反向入栈,即从数据尾部往前遍历,对应单调递增栈
以上是单调栈最基础的应用场景,很多问题也是对这些场景的变种,我们需要一针见血的直指问题核心。
实现模板
在代码实现上,主要涉及两个动作(动作之间的顺序需要根据具体问题场景灵活调整):
- 维护栈顶: 保证整个栈的单调性,新元素入栈时,及时弹出栈顶不满足单调性的元素
- 问题解计算逻辑:在弹出栈顶时,计算问题解
伪代码如下:
ans = 问题初始解
//tips:由于下面流程必须判断栈非空,某些场景下,可以构造一个不影响结果又能保证栈永远非空的初始化栈,这样就避免判断栈非空逻辑 ---
stack<栈内元素类型> stk = 初始化栈;
//正常处理流程
for(const auto& item: dataSource){while (!stk.empty() && checkMonotonic(stk.top(), item)) {//计算问题解ans = 问题解计算逻辑stk.pop();}stk.push(x);
}//在某些场景下,需要保证所有元素出栈 --- 可以通过一些辅助数据来 保证所有数据在上面流程中全部出栈,这样可以省略以下逻辑,保证代码简洁性
while (!stk.empty()) {//计算问题解ans = 问题解计算逻辑stk.pop();
}
单调栈的结构简单,应用形式灵活,需要结合具体问题灵活处理。
具体示例
下一个最大元素I
496. 下一个更大元素 I
问题描述
nums1 中数字 x 的 下一个更大元素 是指 x 在 nums2 中对应位置 右侧 的 第一个 比 x 大的元素。
给你两个 没有重复元素 的数组 nums1 和 nums2 ,下标从 0 开始计数,其中nums1 是 nums2 的子集。
对于每个 0 <= i < nums1.length ,找出满足 nums1[i] == nums2[j] 的下标 j ,并且在 nums2 确定 nums2[j] 的 下一个更大元素 。如果不存在下一个更大元素,那么本次查询的答案是 -1 。
返回一个长度为 nums1.length 的数组 ans 作为答案,满足 ans[i] 是如上所述的 下一个更大元素 。
示例 1:
输入:nums1 = [4,1,2], nums2 = [1,3,4,2].
输出:[-1,3,-1]
解释:nums1 中每个值的下一个更大元素如下所述:
- 4 ,nums2 = [1,3,4,2]。不存在下一个更大元素,所以答案是 -1 。
- 1 ,nums2 = [1,3,4,2]。下一个更大元素是 3 。
- 2 ,nums2 = [1,3,4,2]。不存在下一个更大元素,所以答案是 -1 。
示例 2:
输入:nums1 = [2,4], nums2 = [1,2,3,4].
输出:[3,-1]
解释:nums1 中每个值的下一个更大元素如下所述:
- 2 ,nums2 = [1,2,3,4]。下一个更大元素是 3 。
- 4 ,nums2 = [1,2,3,4]。不存在下一个更大元素,所以答案是 -1 。
问题分析
本题的问题描述看着挺复杂的,但由于nums1是nums2的子集,即nums1中的数值都在nums2中,且无重复数字,所以,这里的问题可以简化先为求nums2中每个元素的下一个最大元素,然后再取nums1中特定元素对应的下一个最大元素。
代码实现
class Solution {
public:vector<int> nextGreaterElement(vector<int>& nums1, vector<int>& nums2) {//适用hash map存储每个元素对应的下一个最大元素值unordered_map<int,int> preData;stack<int> stk;//使用单调递减栈求取每个元素的下一个最大元素for(int idx = nums2.size() - 1; idx >= 0; --idx){while(!stk.empty() && nums2[idx] >= stk.top()){stk.pop();}preData[nums2[idx]] = stk.empty() ? -1 : stk.top();stk.push(nums2[idx]);}vector<int> ans;//遍历每个元素取值for(int num: nums1){ans.push_back(preData[num]);}return ans;}
};
柱状图中最大的矩形
84. 柱状图中最大的矩形
问题描述
给定 n 个非负整数,用来表示柱状图中各个柱子的高度。每个柱子彼此相邻,且宽度为 1 。
求在该柱状图中,能够勾勒出来的矩形的最大面积。
示例 1:
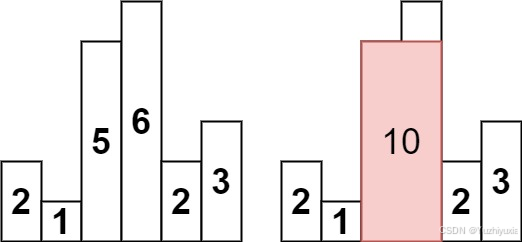
输入:heights = [2,1,5,6,2,3]
输出:10
解释:最大的矩形为图中红色区域,面积为 10
示例 2:

输入: heights = [2,4]
输出: 4
问题分析
矩形面积的计算公式为 矩形面积 = 宽 ∗ 高 矩形面积= 宽 * 高 矩形面积=宽∗高,求最大面积需要遍历所有柱子,以该柱子为高的所有矩形面积中的最大面积。当计算某根柱子为高的矩形面积时,只需要确定宽度,即确定矩形的左右边界:
- 左边界:该柱子往左找到第一个比他矮的柱子
- 右边界:该柱子往右找到第一个比他矮的柱子

对应的代码实现如下:
class Solution {
public:int largestRectangleArea(vector<int>& heights) {int ans = 0;int size = heights.size();for(int idx = 0; idx < size; ++idx){//查找左边界:往左找第一个比他矮的柱子int left = idx;while(left > 0 && heights[left - 1] >= heights[idx]) left--;//查找右边界:往右找第一个比他矮的柱子int right = idx;while(right < size - 1 && heights[right + 1] >= heights[idx]) right++;ans = max(ans, heights[idx] * (right - left + 1));}return ans;}
};
这道题作为难度级别为Hard的题目,该实现提交后肯定会超时,超时的原因就是在确定左右边界时会做大量的来回比较,如果我们能够快速找到左右边界,那就ok了。在确定左右边界时,需要找到第一个比他矮的柱子,这不这是单调队列的经典应用场景吗?
对于该问题,需要往左和往右两个方向利用单调递增栈求其第一个比他矮的柱子。
代码实现
先利用单调递增栈分别求出当前柱子的左右边界,然后再计算所有柱子对应的矩形面积,最后取其中最大的矩形面积。
class Solution {
public:int largestRectangleArea(vector<int>& heights) {int size = heights.size();stack<int> stk;//左边界vector<int> left(size,0);for(int idx = 0; idx < size; ++idx){while(!stk.empty() && heights[stk.top()] >= heights[idx]) stk.pop();left[idx] = stk.empty() ? -1 : stk.top();stk.push(idx);}stk = stack<int>();//右边界vector<int> right(size,0);for相关文章:

单调栈应用介绍
单调栈应用介绍 定义应用场景实现模板具体示例下一个最大元素I问题描述问题分析代码实现柱状图中最大的矩形问题描述问题分析代码实现接雨水问题描述问题分析代码实现最大宽度坡问题描述问题分析代码实现132模式问题描述问题分析代码实现定义 栈(Stack)是另一种操作受限的线性…...

部署前后端分离若依项目--CentOS7Docker版
一、准备 centos7虚拟机或服务器一台 若依前后端分离项目:可在下面拉取 RuoYi-Vue: 🎉 基于SpringBoot,Spring Security,JWT,Vue & Element 的前后端分离权限管理系统,同时提供了 Vue3 的版本 二、环…...
PH47代码框架功能速查
1. PH47框架逻辑层全局引用对象 全局引用 功能简介 快速访问 bus 数据总线系统功能实现,如对总线数据项读写操作等 数据总线bus drv 驱动层功能实现,如飞控板相关的各种硬件传感器设备进行操作等 驱动层drv mcu 对mcu的片内接口及设备进行操作…...

UVM寄存器模型:uvm_reg_adapter
文章目录 一、什么是uvm_reg_adapter1、what2、Example2.1、代码详解 二、如何使用uvm_reg_adapter三、为什么要引入uvm_reg_adapter 一、什么是uvm_reg_adapter 1、what uvm_reg_adapter继承于uvm_object,定义了用于在 uvm_reg_bus_op 和特定总线事务之间进行转换…...

总结OpenGL和pyrender安装和使用过程中的坑
目录 报错一:AttributeError: NoneType object has no attribute glGetError 报错二:ImportError: (Unable to load OpenGL library, OSMesa: cannot open shared object file: No such file or directory, OSMesa, None) 报错三:raise ImportError("Unable to load…...
)
温湿传感器(学习笔记下)
接着我们温湿传感器上半部分的学习,现在我们学习接下来的部分,编写GXHTC3驱动程序,也就是给gxhtc3.c文件添加代码,我们要判断gxhtc3芯片是否存在和正常,就要先读取gxhtc3的ID号,根据gxhtc3的数据手册,读取命…...

期刊论文写作之word模板
一、zotero参考文献使用 下载zotero软件,请搜索相关帖子或者小破站即可; 把pdf拖到zotero软件里面,直接拉进去; 下面建立一个word演示: 1.导入pdf点击红框部分,根据期刊要求选择参考文献样式࿰…...

雷池社区版OPEN API使用教程
OPEN API使用教程 新版本接口支持API Token鉴权 接口文档官方没有提供,有需要可以自行爬取,爬了几个,其实也很方便 使用条件 需要使用默认的 admin 用户登录才可见此功能版本需要 > 6.6.0 使用方法 1.在系统管理创建API TOKEN 2.发…...

LSTM(Long Short-Term Memory,长短期记忆网络)在高端局效果如何
lstm 杂乱数据分析 LSTM(Long Short-Term Memory,长短期记忆网络)在高端局,即复杂的机器学习和深度学习应用中,展现出了其独特的优势和广泛的应用价值。以下是对LSTM在高端局中的详细解析: 一、LSTM的优势…...
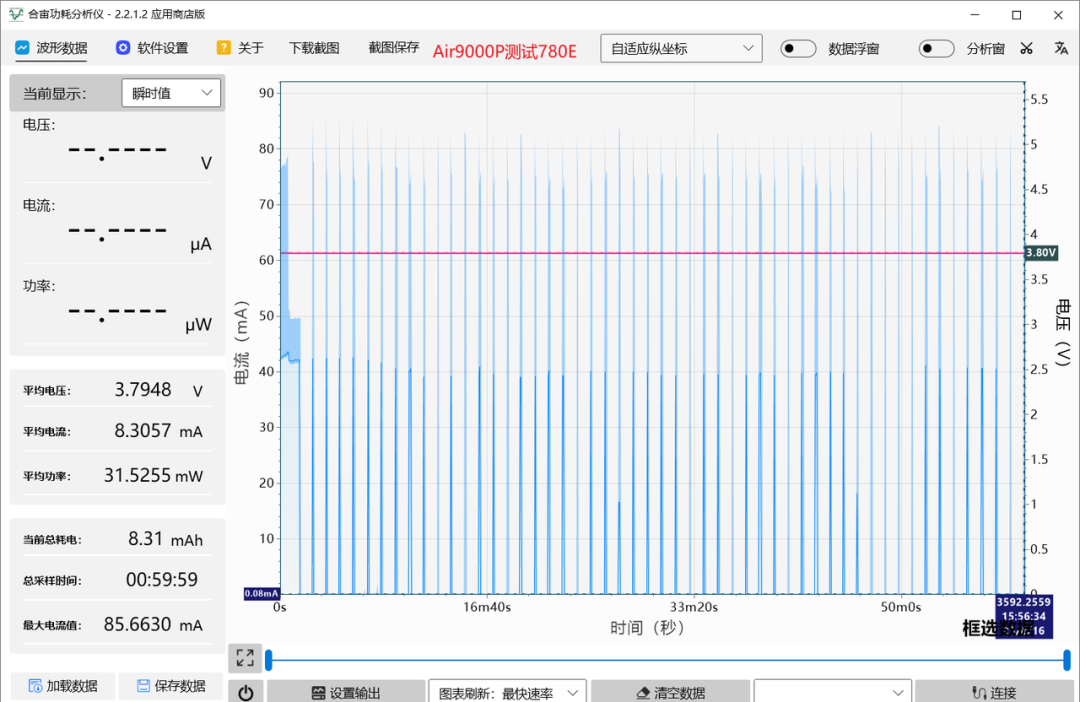
模组操作宝典:4种关机重启技巧,让你的设备运行无忧
今天我说的是关于关机重启技巧。 给4G模组VBAT断电关机,模组关机前未能及时退出当前基站,会有什么影响呢? 基站会误以为设备还在线,下次开机仍会拿着上次驻网信息去连基站。基站一看,上次链接还在——认为你是非法设…...
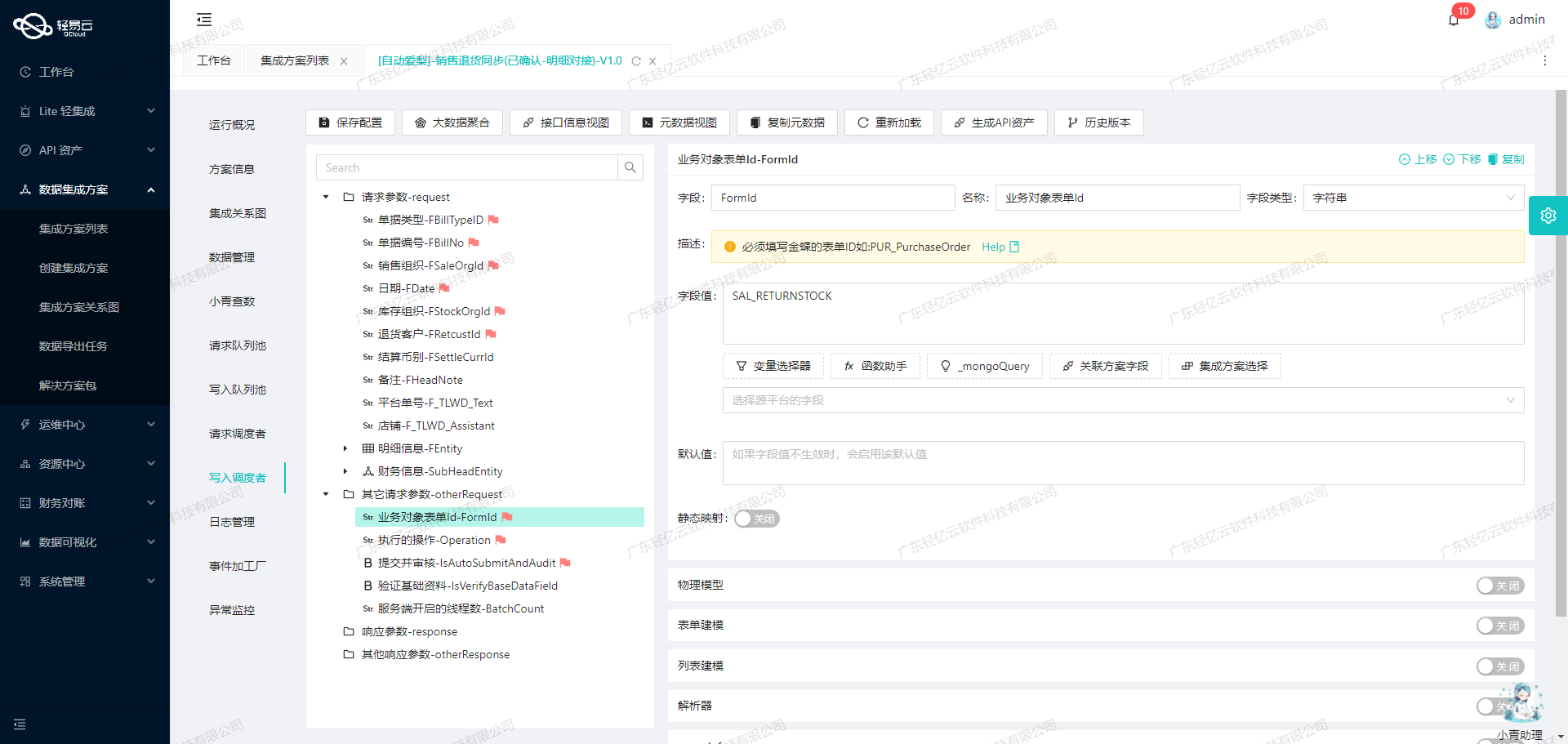
利用API接口实现旺店通和金蝶系统的无缝数据对接
旺店通销售出库对接金蝶销售订单(线下)的技术实现 在企业日常运营中,数据的高效流转和准确对接是确保业务顺畅运行的关键。本文将聚焦于一个具体案例:如何通过轻易云数据集成平台,实现旺店通企业奇门的数据无缝对接到金蝶云星空系统。我们将…...
)
热题100(hash)
热题100(Hash) 三道题目 1.两数之和(√) 49.字母异位词分组(题解) 128.最长连续序列(题解) 思路 第1题简单hash映射,O(n) 第49题,关键点在于Hashmap的形式,‘HashMap<Stri…...

Ubuntu下Mysql修改默认存储路径
首先声明,亲身经验,自己实践,网上百度了好几个帖子,全是坑,都TMD的不行,修改各种配置文件,就是服务起不来,有以下几种配置文件需要修改 第一个文件/etc/mysql/my.cnf 这个文件是存…...

LVGL移植教程(超详细)——基于GD32F303X系列MCU
版本:LVGL Kernel V8.3.0,运行压力测试Demo Stress首先放一张最终Stress Demo 运行图: 一、准备 1. GD32 Keil工程 准备任意一个屏幕可以正常显示的GD32工程: 2. LVGL源码 最新版现在已经是V9.2了,这里我选择了…...

《计算机原理与系统结构》学习系列——处理器(中)
系列文章目录 目录 流水线数据通路与控制概述5个流水级指令周期与流水级 流水线性能流水线时钟周期的长度T和数量cycles流水线性能 流水线数据通路流水线寄存器流水线分析图形化流水线流水线控制 流水线数据通路与控制 概述 5个流水级 指令周期与流水级 单周期实现中&#x…...

深入解析 OceanBase 数据库中的局部索引和全局索引
深入解析 OceanBase 数据库中的局部索引和全局索引 引言 在分布式数据库中,索引的设计对于优化查询性能至关重要。OceanBase 作为一款高性能的分布式关系数据库,支持局部索引和全局索引两种索引类型。理解这两种索引的特点和适用场景,对于数…...
2024防晒衣市场社媒营销洞察报告
2024年,硬防晒已经从单一的户外场景,扩展到通勤、外出游玩、穿搭等更多场景,多样化的需求导致的消费群体不断扩大,“防晒经济”迎来自己的主场时刻。 当前,防晒衣不仅需要满足不用场景的灵活切换,还要满足多…...

【Ubuntu20.04 Visual Studio Code安装】【VSCODE】
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、打开VSCOE官网二、下载VSODE的Ubuntu版本三、安装VSCODE软件包四、导入工作空间(添加工作空间目录)五、安装插件:1.安装简体中文包2.安装ros插件…...

贪心算法day(1)
1.将数组和减半的最少操作次数 链接:. - 力扣(LeetCode) 思路:创建大跟堆将最大的数进行减半 注意点:double t queue.poll()会将queue队列数字减少一个后再除以2,queue.offer(queue.poll()/…...

窗口函数sql使用总结
一、开窗 基础知识:窗口分析函数 (1)LAG(col,n,DEFAULT) 用于统计窗口内往上第n行值 第一个参数为列名,第二个参数为往上第n行(可选,默认为1),第三个参数为默认值(当往…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...
